泊位—岸桥多目标联合调度

乐美龙,于 航， 黄 薇

(上海海事大学 物流研究中心,上海 201306)

泊位和岸桥的联合调度问题(berth allocation and quay crane assignment problem,BACAP)是指码头计划人员根据码头的泊位和岸桥等约束条件,利用相关的优化方法为在一定时期内靠泊的船舶确定其靠泊位置、时间和服务于该船舶的岸桥数目.与单纯的泊位分配问题(berth allocation problem,BAP)和岸桥分配问题(quay crane allocation problem,QCAP)相比,泊位和岸桥的联合调度把两者看成一个整体来考虑,能有效反映其相互制约的关系.同一艘船安排的岸桥数目与船舶的在港时间成反比.增加岸桥数目可以减少在港时间,但不一定缩短了服务成本.把泊位和岸桥联合调度更符合码头的实际运作.

国外对于泊位和岸桥的联合调度问题研究,如文献[1]中对离散的BACAP建立了优化模型,并用遗传算法进行求解；文献[2]中建立了以船舶作业时间、船舶等待时间和船舶推迟离港时间之和最小化为目标,并采用遗传算法与启发式算法相结合来求解；文献[3]中从船舶靠泊位置对岸桥作业效率的影响,建立了以船舶服务费用最小化为目标的优化模型,并用启发式算法求解；文献[4]中建立了一个整数规划泊位和岸桥联合调度的优化模型,用拉格朗日松弛的启发式算法进行求解.

国内对于泊位和岸桥的联合调度的研究相对较少,如文献[5]中研究了随机环境下集装箱码头泊位和岸桥调度的优化,以船舶等待时间最小化为目标建立模型,并用遗传算法求解;文献[6]中以船舶最小在港时间为目标建立了模型,并用免疫遗传算法求解,得到了协调调度优化比单独调度优化更好的结果.

目前,绝大多数研究将泊位分配和岸桥分配分开考虑,两者的协调调度研究较少,而且大多也是基于最小化船舶在港时间为目标的优化.所以,在实际的情况下,文中提出了同时最小化船舶在港时间和码头运营成本的优化模型,以寻求码头综合效益最大的泊位和岸桥的分配方案.

1 问题描述

提高连续泊位和岸桥调度的效率,可以有效地减少港口运作成本,提高港口的竞争力.连续泊位和岸桥的调度问题可用图1说明.在这个时间空间的二维图里,矩形代表在港的船舶;矩形的高代表船长;ai为船舶靠泊时间;xi为船舶靠泊位置;bi为船舶偏好靠泊位置;si为船舶作业结束时间;每个黑色小矩形表示一个岸桥的工时,如船舶1在靠泊作业的8个小时内,依次分配的岸桥数是4,4,4,4,3,3,2,2.

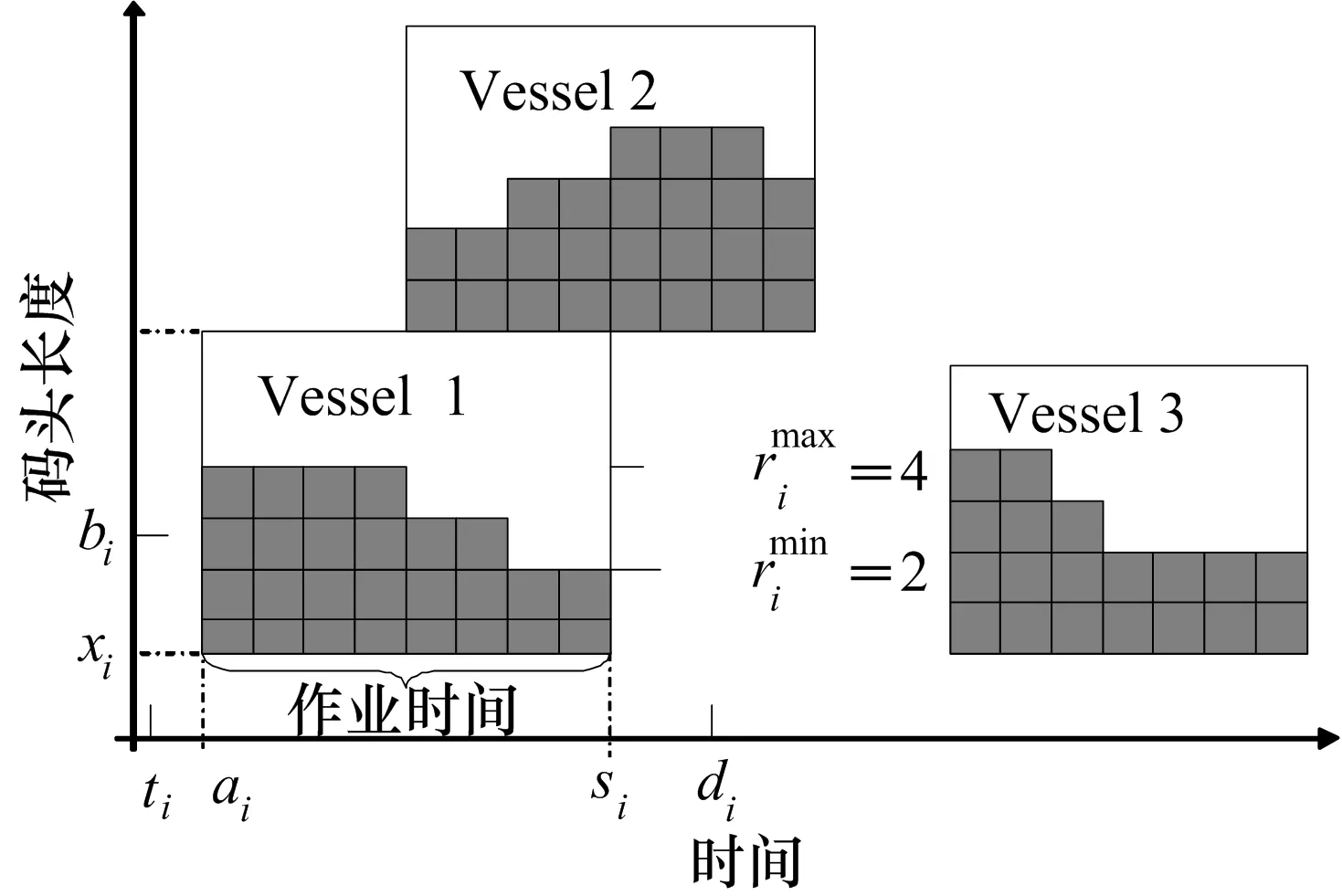
图1 船舶泊位和岸桥的联合调度二维图Fig.1 Time-space diagram for a continuous BACAP

为了便于问题的分析,更好的建立模型,文中做出以下假设:①每艘船必须仅被服务一次;②船舶到达后进行靠泊服务;③每艘船都有一个偏好靠泊位置;④岸线上各处的水深完全符合任何船舶的靠泊要求,即船舶可以在任意的位置靠泊;⑤船舶的靠泊位置加上船长不能超过泊位的长度;⑥每艘船都有最少和最多安排的岸桥数目;⑦岸桥的移动时间可以忽略;⑧码头上的岸桥移动均位于一轨道上,不能跨越交叉.

船舶一般会希望靠泊在靠近特定堆场的泊位,这个位置就是船舶偏好的靠泊位置.如果实际分配的靠泊位置与偏好位置不一致,将增加集卡运输距离和岸桥工时,导致整体作业效率下降,从而船舶需要更多的岸桥工时.所以,引入靠泊位置偏离因子β,船舶的靠泊位置与偏好位置的偏差量Δ=|xi-bi|,其单位距离单位工时的惩罚成本为c3i,则可表示为c3i·(1+β|xi-bi|).当β=0.01时,若靠泊位置偏离其偏好位置一单位,其惩罚成本就增加1%.

当几个岸桥同时服务一艘船时,相互之间也会产生干扰,在1985年Schonfeld和Sharafeldien引入了岸桥干扰指数α(0≤α≤1),当每小时安排q个岸桥给一艘船,则需要qα个岸桥作业时间.

2 多目标优化数学模型

根据港口的实际运营情况,文中提出了多目标连续泊位和岸桥联合调度的混合整数规划模型,为了方便建立模型,引入以下符号:

1)集合与参数

2)决策变量

xi为船i实际系泊位置;ti为船i实际系泊时间;zit为在t时间内安排给船舶i的岸桥数目;ritq∈{0,1}，在t时间内有q个岸桥服务船i，则ritq=1；否则ritq=0;δij∈{0,1}，在时间轴上,若船i泊位于船j的左边，则δij=1；否则δij=0;σij∈{0,1}，在位置轴上,若船i泊位于船j的下方，则σij=1；否则σij=0.

3)目标函数

在模型假设和模型符合定义的前提下,建立了如下的多目标泊位和岸桥联合调度模型:

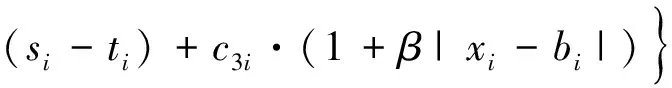
(1)

(2)

4)约束函数

xi+li≤L∀i∈V

(3)

ai≤ti≤T∀i∈V

(4)

xi+li≤xj+M(1-δij) ∀i,j∈V,i≠j

(5)

si≤tj+M(1-σij) ∀i,j∈V,i≠j

(6)

δij+δji+σij+σji≥1 ∀i,j∈V,i≠j

(7)

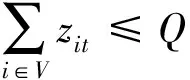
(8)

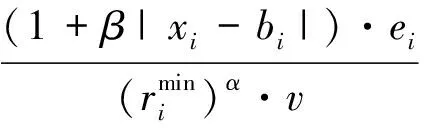
(9)

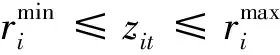
(10)

si≤di∀i∈V

(11)

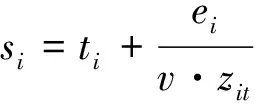
(12)

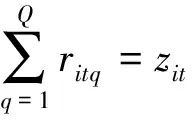
(13)

-1≤rit(q-1)+rit(q+1)-ritq≤1

∀q∈Q,i∈V,t∈T

(14)

δij,δji,σij,σji∈{0,1} ∀i,j∈V,i≠j

(15)

ti,xi,qi≥0 ∀i∈V

(16)

目标函数(1)表示最小化船舶总的在港运营成本,为了方便计算，可以将目标函数化简，转化为线性函数，转化后模型为

minf1=

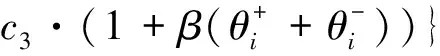
(17)

约束条件:

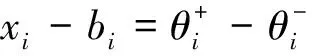
(18)

将约束条件式(18)代入约束条件式(9)，也可线性化简转化为

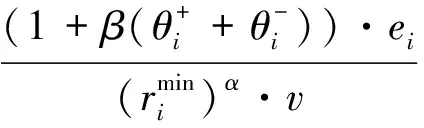
(19)

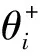
3 算例

文中船舶的泊位和大小的实时数据采集于宁波某著名集装箱港口,其码头长度为1 600 m,岸桥14台,船舶的偏好位置是随机产生的,岸桥的装卸速率v=35箱/h,以1 h作为一个时间窗.根据文献[7],文中将成本系数c1i，c3i分别设定为＄2 000li/230和＄10li/230.根据码头运营数据统计,取c2=100元,表示每台岸桥的运作费用.船舶资料以2012年7月16日的数据为基础(表1).

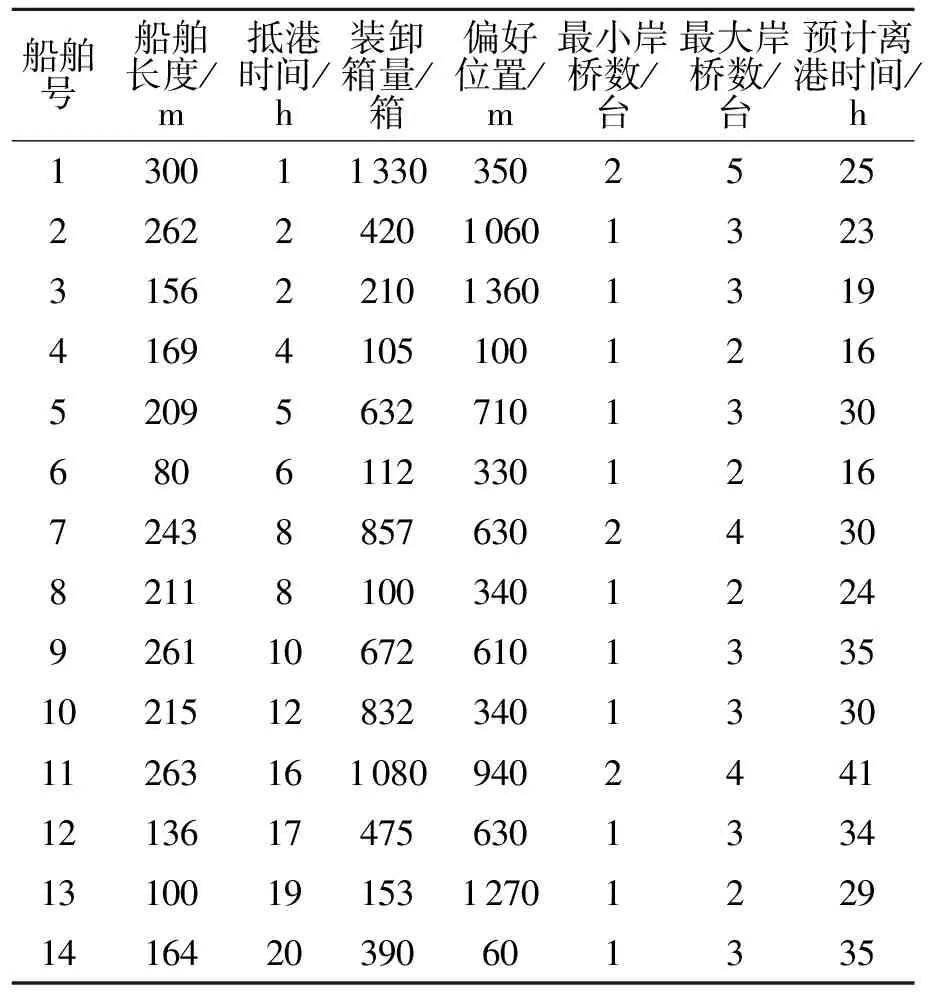
表1 到港船舶数据Table 1 Data for the arrival vessels

注:船长包括船与船之间的安全距离.

3.1 单目标优化求解

根据文中的模型和相关数据，利用Gurobi软件进行求解,首先对单目标1和单目标2分别进行求解,目标1的最优化结果为6 315元,目标2的最优化结果为63 h,目标2的优化结果见表2.

3.2 多目标优化求解

多目标优化求解是在目标1优化的情况下,将其改为约束,对目标2进行优化，即对船舶总的在港时间最小化进行求解,求解结果见表3.

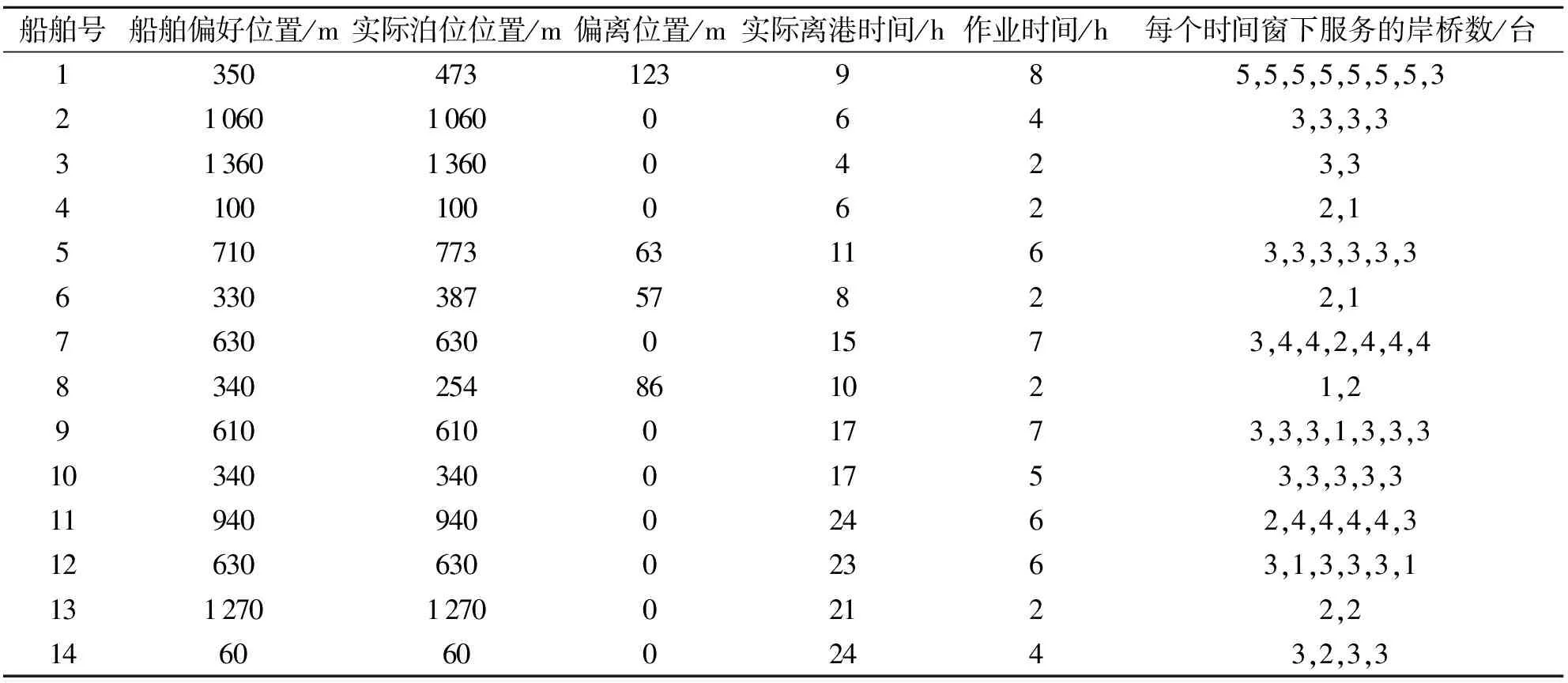
表2 目标2优化结果Table 2 Optimization results of objective 2

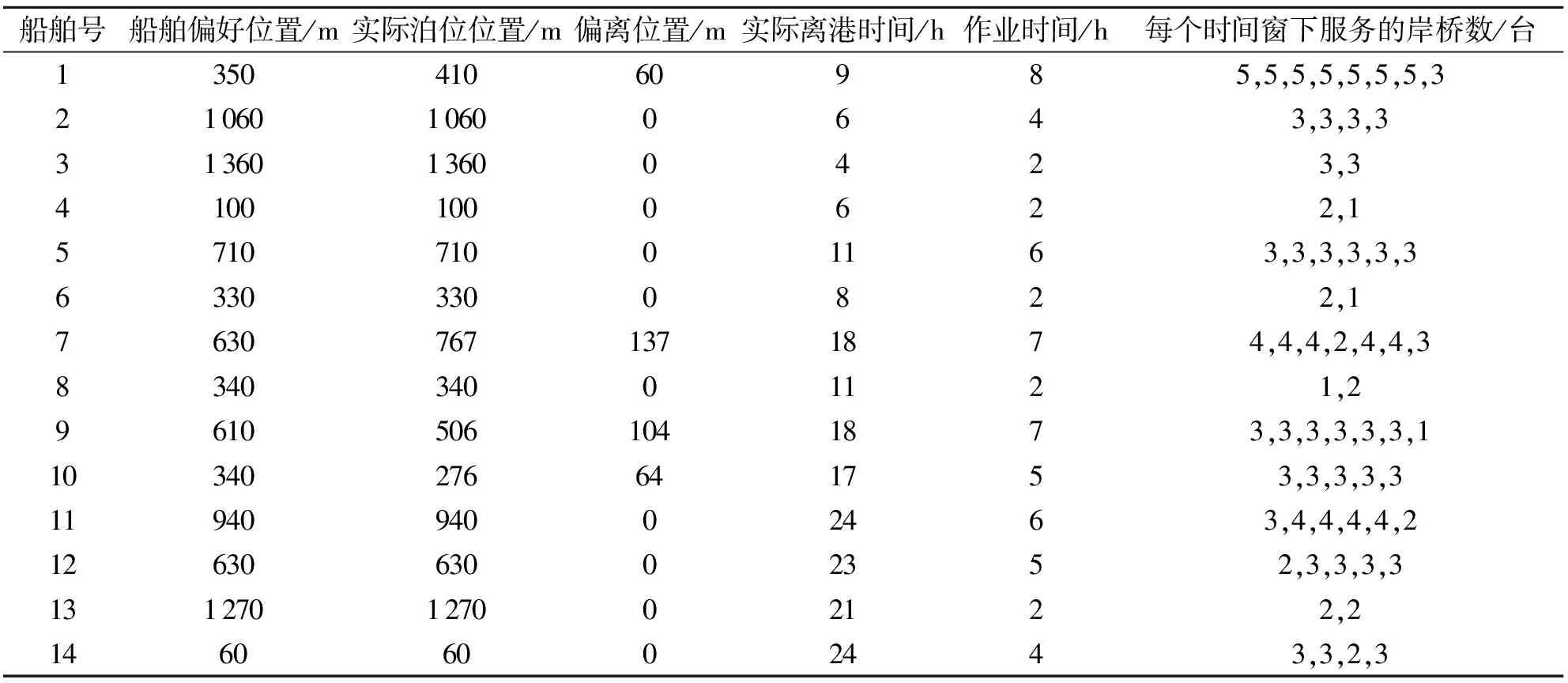
表3 目标1优化后的求解数据Table 3 Optimized solution data of objective 1

计算结果显示,在单目标2的优化值为63,其中有4艘船偏离了船舶偏好位置.在目标函数1优化下,目标函数2的值为70,船舶总等待时间为8 h,处理时间为62 h,14艘船舶里面也只有4艘船舶偏离泊位偏好位置,船1偏离60 m,船7偏离137 m,船9偏离104 m,船10偏离64 m.由于目标函数值越小,越能符合优化的效果,而单目标优化在港时间小于多目标优化的在港时间,偏差量为11.1%.所以,多目标优化结果劣于单目标的优化结果.但是,多目标优化更符合实际情况,同时考虑了船舶在港时间和码头运营成本的最小化,使码头获得更大的综合效益.图2是多目标优化泊位和岸桥分配的二维图.

图3是每个时间窗岸桥的利用情况,从图中可以看出,在时段1,9～12,18,19和24岸桥的利用率相对较低,说明这些时段船舶达到率不高,其他时段岸桥利用率较大,船舶的到达比较集中.岸桥的最大利用量为12,而实际的岸桥总数为14,最大利用率是86%,而在实际码头运营中,岸桥的利用率也是不可能达到100%,因为岸桥都要定时进行检查和维护.所以,如果在船舶到达更集中的情况下,岸桥的数量就会不够,从码头的长远发展来看,可以适当的增加1～2台岸桥,以提高船舶的作业效率,使码头获得更大的综合效益,符合码头决策者的需求.

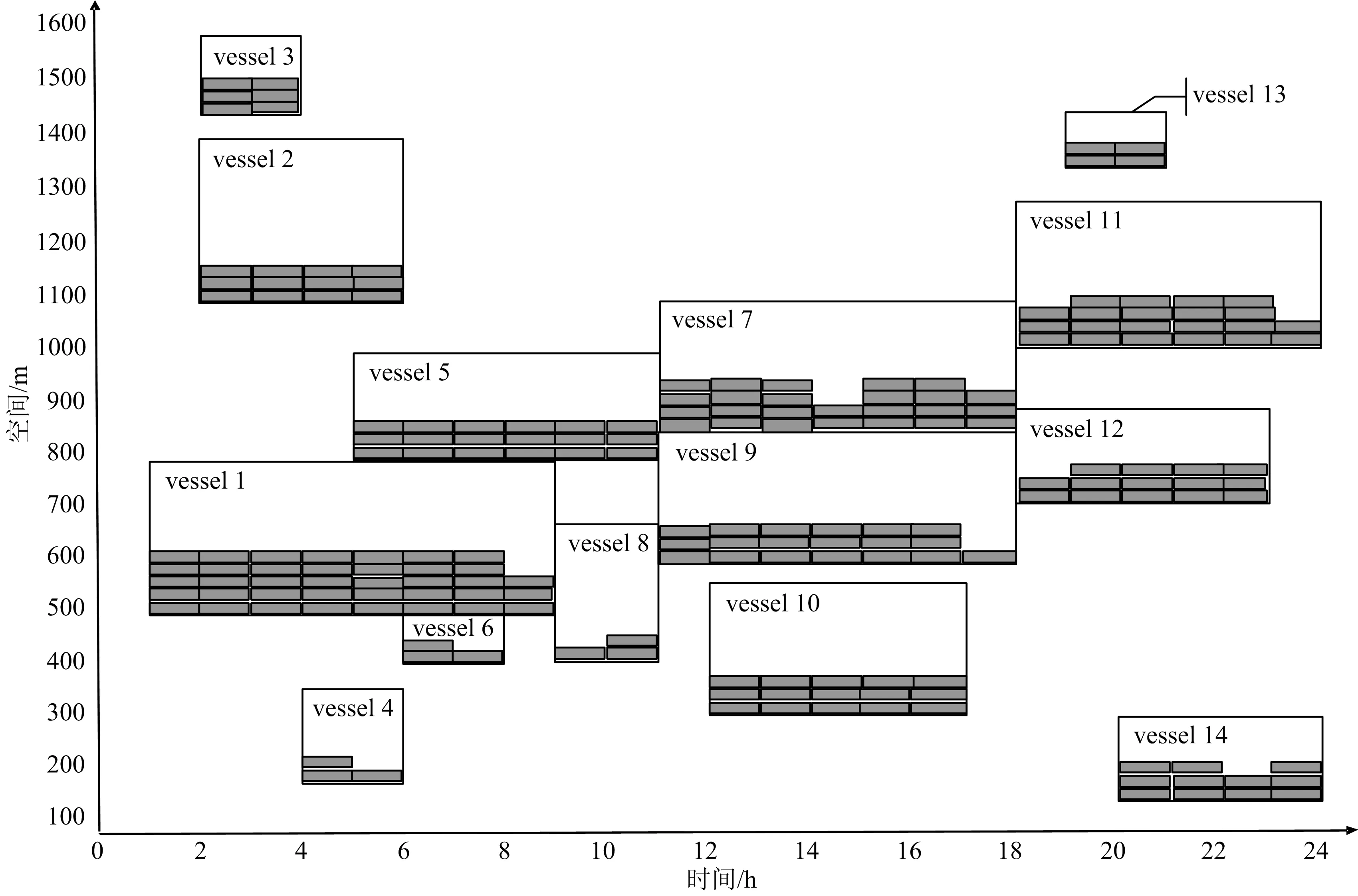
图2 多目标优化计算结果Fig.2 Multi-objective optimization results

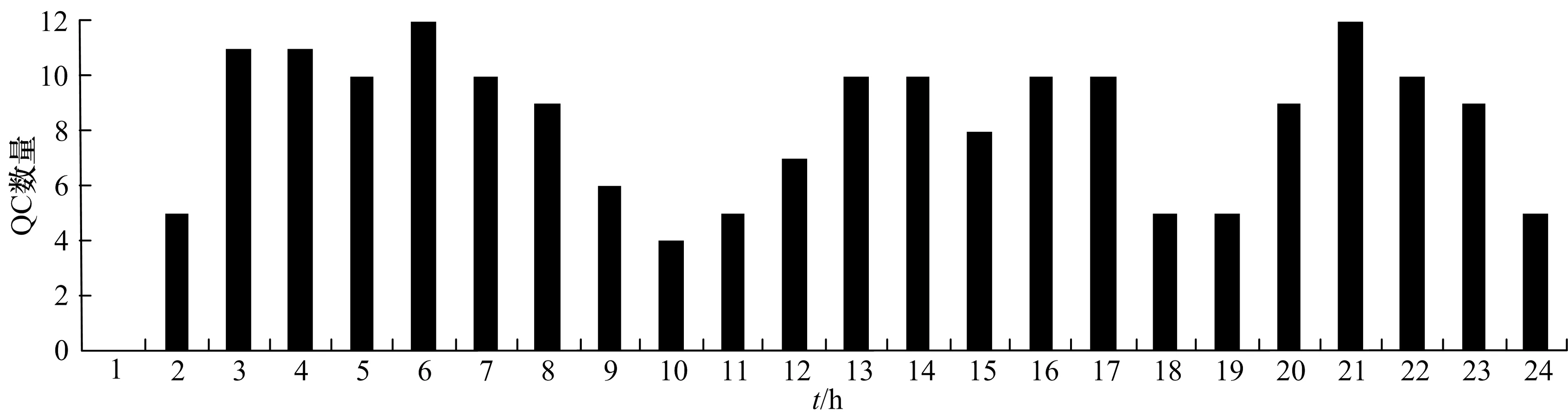
图3 QC的利用量Fig.3 Utilization of QC

4 结论

文中研究了集装箱港口泊位与岸桥联合调度,同时考虑最小化船舶的在港时间和运营成本,建立了相应的多目标优化模型,并采用 Gurobi进行求解,分析了单目标优化和多目标优化的差异性,并且多目标优化更符合码头实际的运营情况.但是,在该模型中没有考虑岸桥跨越范围与集卡和龙门吊调度的耦合关系.在以后的研究中,可以将整个港口为研究对象,将这些因素综合考虑,使之更符合实际情况,有利于指导港口的实际工作.

[1] Imai A,Chen H C,Nishimura E，et al. The simultaneous berth and quay crane allocation problem [J].TransportationResearchPartE,2008(44):900-920.

[2] Liang C,Huang Y,Yang Y.A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning [J].Computers&IndustrialEngineering,2009(56):1021-1028.

[3] Meisel F,Bierwirth C. Heuristic for the integration of crane productivity in the berth allocation problem[J].TransportationResearchPartE,2009,45(4):196-209.

[4] Park Y M,Kim K H. A scheduling method for berth and quay cranes[J].ORSpectrum,2003(25):1-23.

[5] 周鹏飞,康海贵. 面向随机环境的集装箱码头泊位—岸桥分配方法[J].系统工程理论与实践,2008(1):161-169.

Zhou Pengfei,Kang Haigui.Study on berth and quay-crane allocation under stochastic environments in container terminal[J].SystemEngineering-theory&Practice,2008(1):161-169.(in Chinese)

[6] 韩骏,孙晓娜,靳志宏.集装箱码头泊位与岸桥协调调度优化[J].大连海事大学学报,2008,34(2):117-121.

Han Jun,Sun Xiaona,Jin Zhihong.Coordinated optimization method for berth and quay crane allocation in container terminal[J].JournalofDalianMaritimeUniversity,2008,34(2)：117-121.(in Chinese)

[7] Bierwirth C,Meisel F.A survey of berth allocation and quay crane scheduling problem in container terminals[J].EuropeanJournalofOperationalResearch,2010(202):615-627.

[8] Lee Derhorng,Wang Huiqiu.Integrated discrete berth allocation and quay crane scheduling in port container terminals[J].EngineeringOptimization,2010,42(8):747-761.

[9] Tavakkoli-Moghaddam R,Makui A,Salshi S,et al.An efficient algorithm for solving a new mathematical model for a quay crane scheduling problem in container ports [J].Computers&IndustrialEngineering,2009(56):241-248.

[10] 乐美龙，刘菲.基于Memetic算法的泊位和岸桥分配问题[J].武汉理工大学学报，2011，33(1)：60-65.

Le Meilong,Liu Fei.Integrated berth allocation and quay crane scheduling by memetic algorithms[J].JournalofWuhanUniversityofTechnology,2011,33(11)：60-65.(in Chinese)

[11] 雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,2009:30-105.