基于正交试验设计的固有应变法在焊接变形预测的应用

周方明,吴 頔,朱正祥,吴兴祥

(1.江苏科技大学 江苏省先进焊接技术重点实验室,江苏 镇江 212003)(2.上海沪临重工有限公司,上海 201306)

焊接变形和残余应力是影响焊后产品精度和性能的重要因素,预测焊接变形对于解决焊接变形问题有着重要的意义[1].其中固有应变有限元法是一种既能解决大型复杂结构,又比较经济实用的预测焊接变形的方法,能够直接解决工程实际问题,有很好的实用意义和发展前景[2].文献[3-5]利用这一概念发展了基于线弹性有限元的固有应变模型.在此基础上,文献[6]通过分析固有应变的产生机制,认为固有应变主要是由焊缝各点的最高到达温度和约束度决定.文献[7]先求出焊点附近存在的固有应变,用所得数据在焊接断面上进行积分求出等效载荷,通过有限元软件求得整个结构的焊接变形.文献[8]提出先求典型结构的固有变形,将其转换成固有应变,并作为初始应变施加于壳单元模型进行弹性计算得到大型结构的变形.文献[9]基于固有变形数据库通过热弹塑性有限元分析得到铝合金对接接头的焊接变形.文献[10]采用基于固有应变理论分层计算的有限元法用于筒体对接焊接变形的计算并为全焊接阀体球阀焊接工艺参数的优化及阀体结构的加工提供了重要的参考数据.目前固有应变法大多采用实验测得或计算得到的平均应变来替代实际构件的未知应变,然后通过热变形或等效载荷力法加载进行计算,但在计算时忽略同一焊缝先焊部分对后焊部分的影响,以及多道焊缝焊接顺序的影响,这必然引起一定误差.基于此，文中通过正交试验设计方法来确定焊接方向、焊接顺序的影响因子,从而使固有应变法更准确地应用于计算多道连续焊接变形.

1 有限元建模

以T型接头为研究对象,有限元模型如图1.网格单元数为11 350,节点数为21 128,单元为solid45.焊接参数:焊接速度为360 mm/min,电弧电流为130 A,电弧电压为20 V,热效率为0.8,线能量为347 kJ/m.T型接头底板尺寸为400 mm×400 mm×6 mm,腹板尺寸为400 mm×150 mm×8 mm,焊角尺寸为6 mm.焊接方式为单道顺序焊接,即先焊一侧再同方向焊另一侧.

图1 T型接头的有限元模型Fig.1 Finite element model of T-joint

2 多道焊固有应变的确定

根据热弹塑性法计算结果[11]可以看出腹板的横向和纵向变形较小,而底板的变形比较明显,为了简化计算,在利用固有应变法时只考虑底板的变形情况.

2.1 底板纵向固有应变的确定

底板纵向固有应变的表达式如下[12]

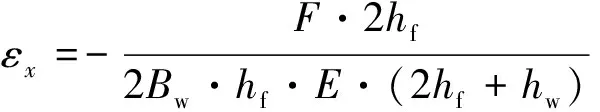
(1)

式中:E为弹性模量(Pa),F为总的纵向收缩力(N),Bw为底板处产生固有应变区域的宽度(m),可以通过热弹塑性法计算结果得到;hf为底板厚度(m),hw为腹板厚度(m).其中纵向收缩力F的表达式如下[13]：

F=α·(Qnet-28.56)

(2)

式中:α为比例系数,取172;Qnet为焊接线能量(kJ/m).

2.2 底板横向固有应变的确定

底板横向固有应变的表达式如下[12]：

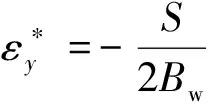
(3)

式中:S为横向收缩变形(m),可以通过热弹塑性计算结果求得.

考虑由于纵向收缩力对于横向收缩变形所产生的影响,则横向应变最终表达式[12]如下：

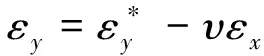
(4)

式中:υ为泊松比,εx为纵向收缩应变.

3 固有应变等效载荷的获得

通过之前得到的固有应变值,可利用以下公式[14]计算得到等效载荷力,并且施加到焊缝区域,经过一次弹性有限元计算得到变形结果.

横向收缩力:

Fy=K·U·σy·Ay=K·U·E·εy·Ay

(5)

纵向收缩力:

Fx=K·U·σx·Ax=K·U·E·εx·Ax

(6)

横向角变形力:

F1=L·Fy

(7)

纵向角变形力:

F2=L·Fx

(8)

式中:K,L分别为焊缝收缩力以及角变形力的影响因子,主要体现焊接方向的影响;U为多道焊影响因子,主要体现焊接顺序的影响;Ay,Ax分别为每段焊缝横向、纵向方向对应的横截面积(m2).

为了研究焊接方向和顺序产生的影响,将每道焊缝分成3段,由于左右各一道焊缝,因而共计6段焊缝,对焊缝按顺序进行编号,编号名为HF1～HF6.利用生死单元技术,通过“EKILL，EALIVE”命令实现焊缝的填充,从而可以体现焊接的真实过程,提高计算精确度.由式(5～8)可以看出,固有应变等效载荷大小取决于相关因素,于是问题就转化为如何确定K，U，L3个影响因子.

由于每段焊缝对应的影响因子不一致,为了反映每段焊缝与影响因子的对应关系,对图2的模型进行分析,得出结论.

图2为平板对接焊模型,焊接方向如箭头所示,共计3段焊缝,以每段焊缝引起的角变形大小V为例,分别对以下两种情况进行分析讨论.

1)理想情况:不考虑前段焊缝对后段焊缝的预热影响,而只考虑拘束作用,令第1段焊缝角变形大小为V1=V,假设第2段角变形大小为V2=V·L,第3段为V3=V·L·L=V·L2(其中L为焊接方向影响因子,L<1).

a) HF1

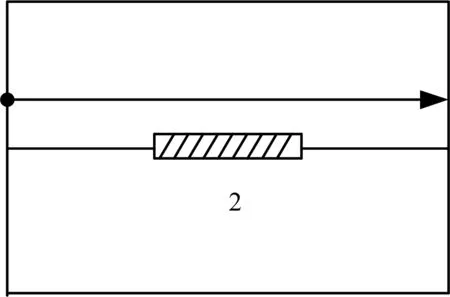
b) HF2

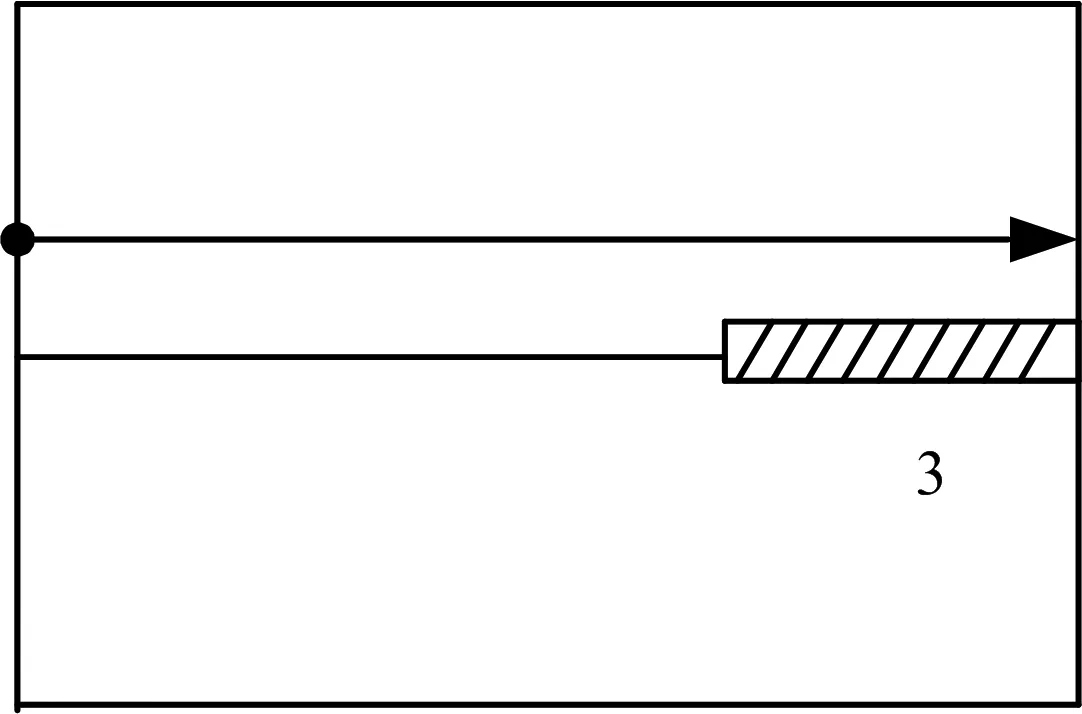
c) HF3

2)实际情况:在实际焊接过程中,需考虑前段焊缝对后段焊缝的预热影响,且变形不是简单地叠加,为了体现焊接过程带来的综合影响,令第1段焊缝角变形大小仍为V1=V,假设第2段角变形大小为V2=V·(1+L)·X,第3段为V3=V·(1+L+L2)·X(其中系数X体现焊接变形平稳增加的趋势),结合之前热弹塑性法计算结果,初步假定X=0.6.焊接方向影响因子K的推导方法跟L一致.

根据推导,文中T型接头第1道3段焊缝HF1～HF3对应的收缩力影响因子分别为1，(1+K)·X，(1+K+K2)X;角变形影响因子分别为1，(1+L)·X，(1+L+L2)·X;而第2道3段焊缝HF4～HF6的影响因子与HF1～HF3的影响因子一一对应.为了验证上述假设的合理性和正确性并求出最佳影响因子值,通过正交试验设计来进行验证计算.

4 正交试验方案设计及分析

4.1 正交表的选用

K，L，U3个因子分别体现了收缩力变化、角变形力变化、多道焊焊接顺序的影响,而收缩力和角变形力的变化同时体现了焊接方向的变化.通过分析,文中设计三水平三因素的正交设计试验,选用L9(34)正交表设计方案,共做9组计算试验,根据热弹塑性法计算的变形结果,初步确定3个影响因子值的范围,各取3个典型值,其中表1为正交设计试验方案.

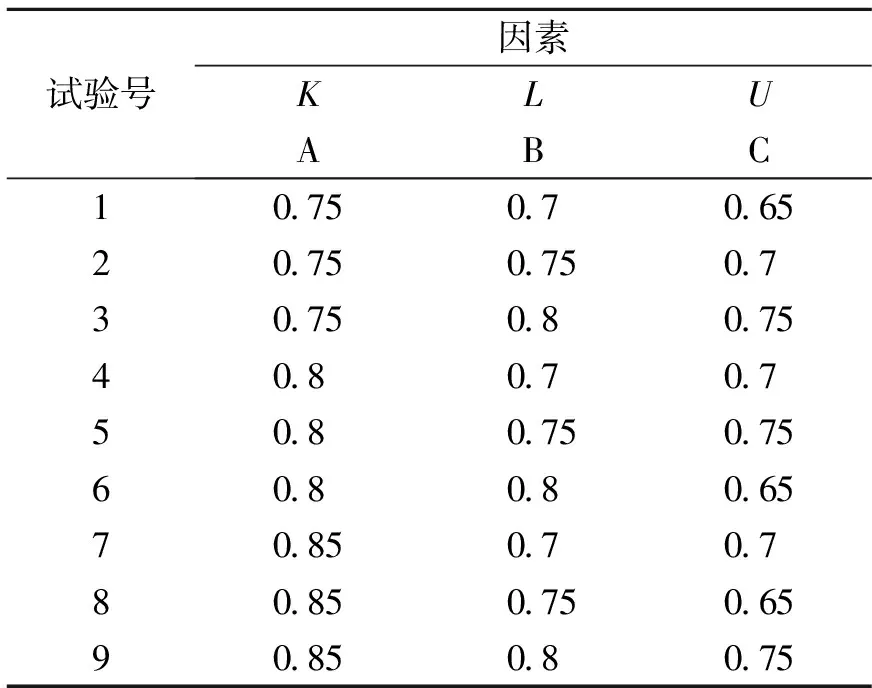
表1 正交设计试验方案Table 1 Scheme of orthogonal experiment design

4.2 正交试验结果计算及分析

根据每组试验的因素大小,通过式(5～8)得到每段焊缝对应的固有应变等效载荷力,第1组等效载荷力大小见表2,固有应变等效载荷加载方式如图3.

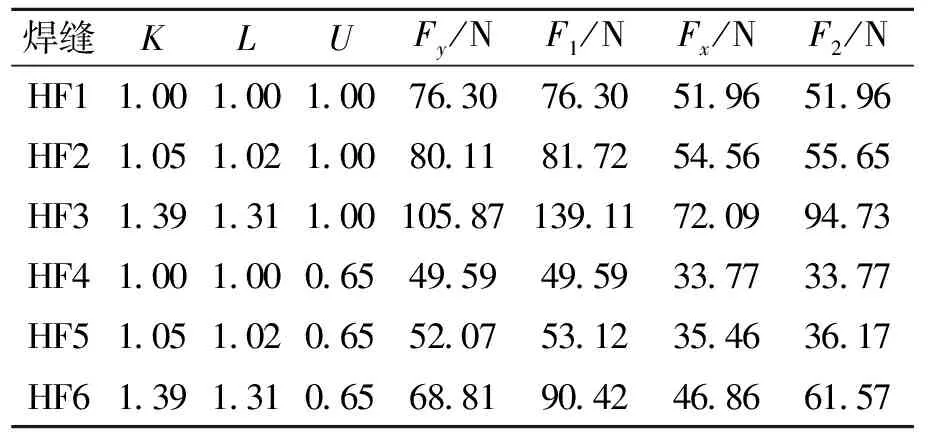
表2 HF1～HF6的焊缝等效载荷Table 2 Weld equivalent load of HF1～HF6

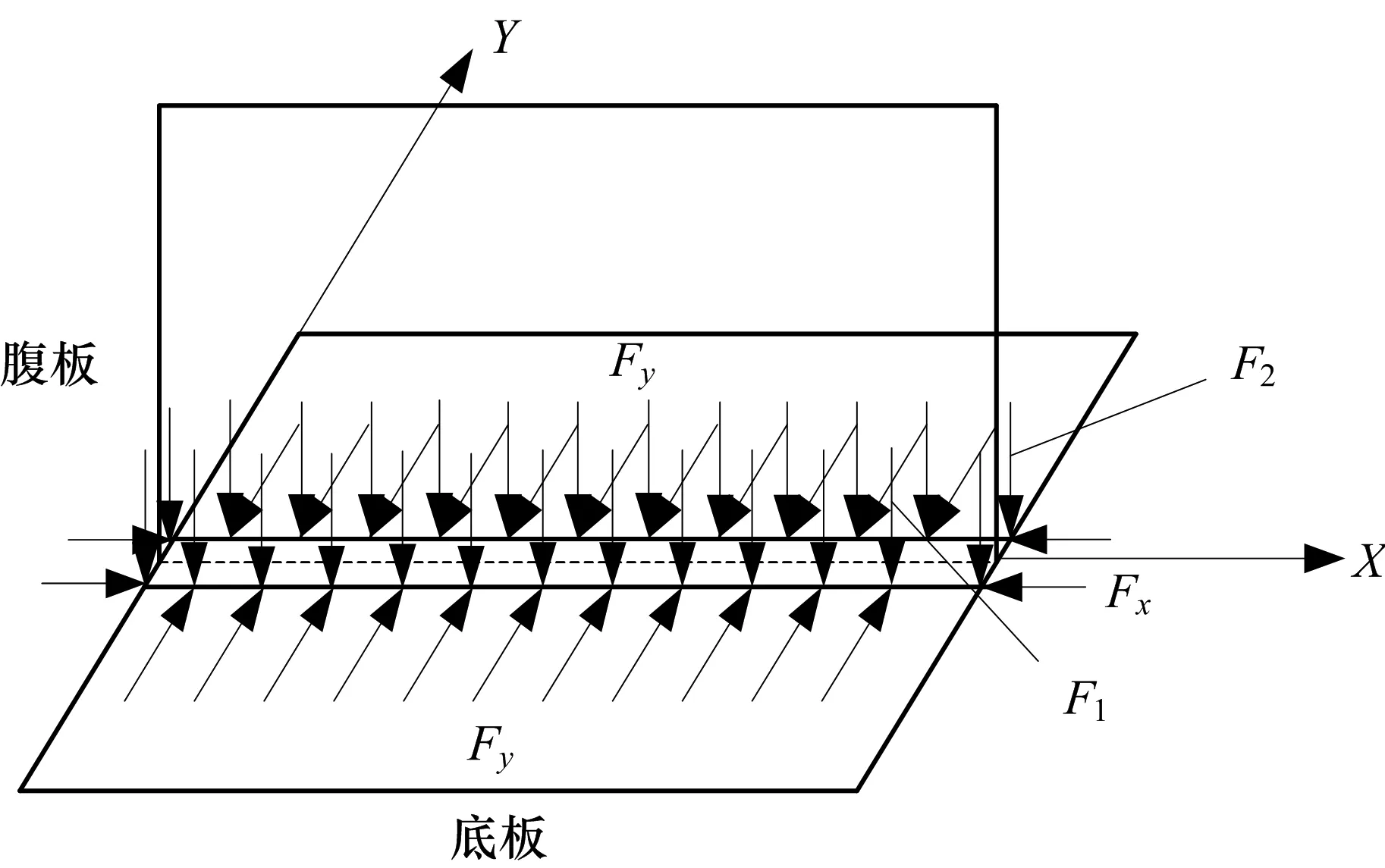
图3 等效载荷加载方式Fig.3 Loading mode of equivalent load

采用正交设计试验方法,以固有应变法与热弹塑性法在底板角变形的位移差为评价指标,即位移差越小,则固有应变法计算越准确.极差分析方法利用数理统计方法计算出正交表中每列的极差R值来判断影响因素的主次关系,寻找较优的水平组合[15].具体的计算为

tij=Tij/r

(9)

Rj=tij(max)-tij(min)

(10)

式中:i为水平数;j为正交表中的列数,即因素数;r为某因素中相同水平重复试验的次数;tij为第j列第i水平的试验平均值;Tij为正交表中第j列第i水平的试验结果;tij(max)为第j列中的最大的tij值;tij(min)为第j列中的最小的tij值;Rj为第j列的极差值.根据上述的极差分析原理,本次正交试验设计极差分析结果如表3.

根据极差分析结果可知,3种因素对位移差的影响的主次顺序为K,L,U,各因素的优化水平分别为K=0.8,L=0.8,U=0.65,最优组合是A2,B3,C1.

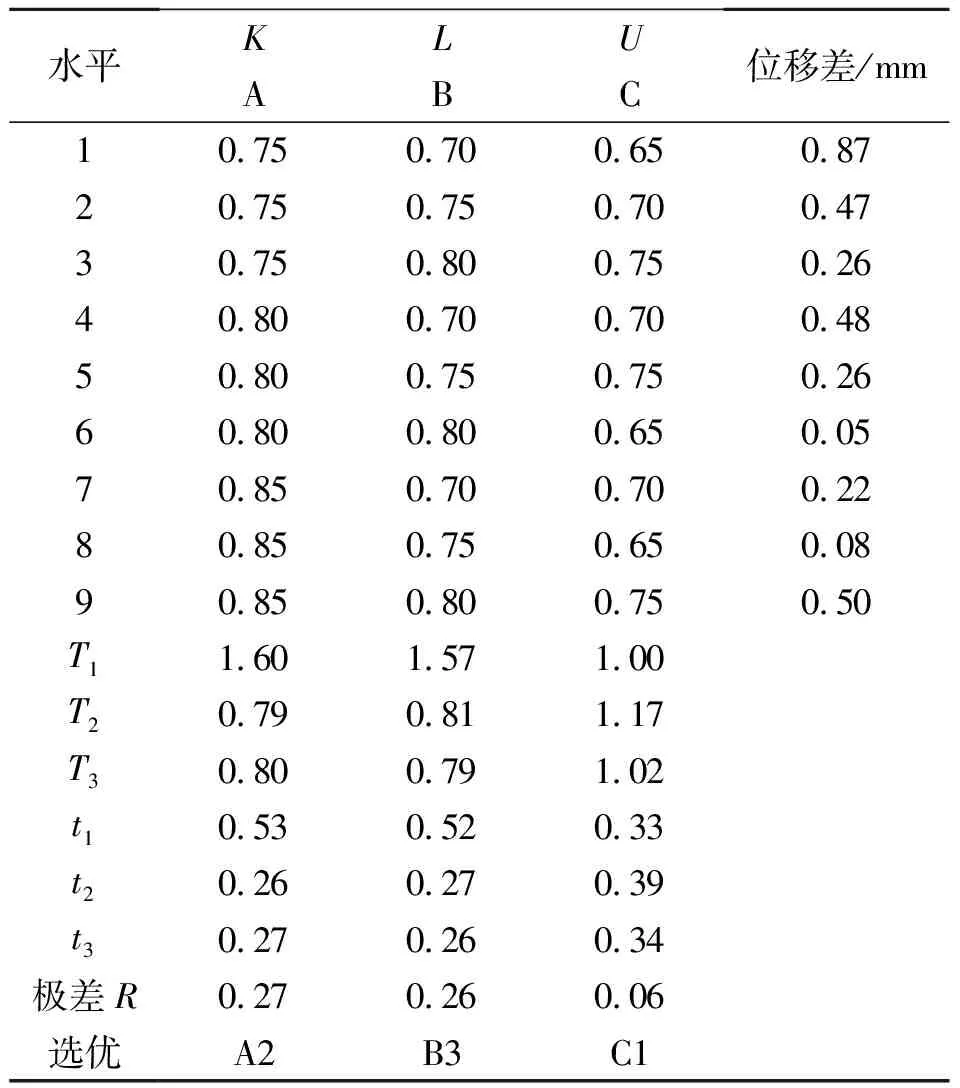
表3 极差分析表Table 3 Range analysis table

5 焊接变形结果分析

图4为最优组合对应的固有应变法计算云图,图5为已知三维热弹塑性计算变形云图,从两图对比可以看出,评定指标位移差为0.05 mm,计算结果比较接近.另外取底板从焊接开始到结束的角变形结果,两种计算方法结果对比见图6,可以看出角变形变化趋势基本一致,都是逐渐增大,从而可以验证正交试验设计方法所得到计算结果正确有效,并且能反映焊接顺序、焊接方向对于焊接变形的影响.

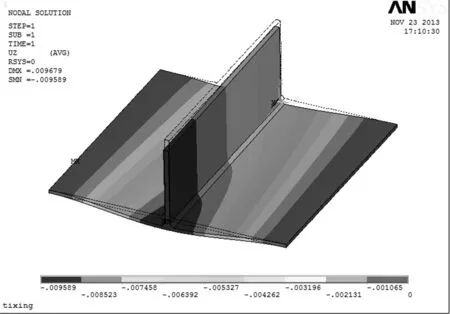
图4 固有应变法变形云图Fig.4 Contour of inherent strain calculation

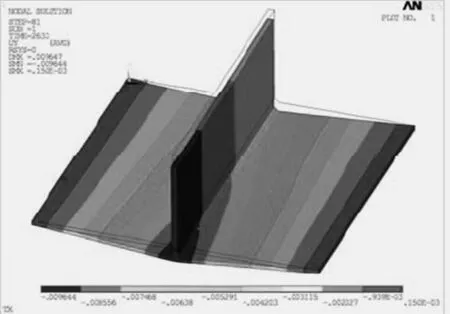
图5 热弹塑性法变形云图Fig.5 Contour of thermal elastic-plastic calculation

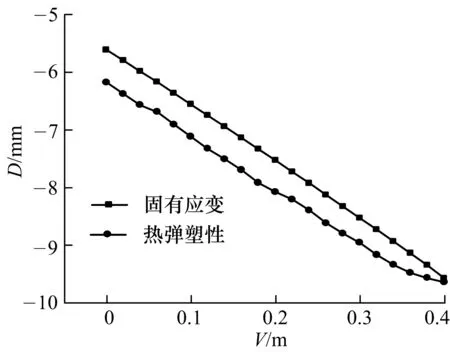
图6 角变形对比曲线Fig.6 Contrast diagram of angular deformation

表4为两种计算方法的比较,从表中可以看出固有应变法所得到的底板角变形量与热弹塑性有限元法的误差为0.57%,小于10%,但相对于热弹塑性有限元法,固有应变法大大缩短了计算时间,只需要45 s,从而验证了采用基于正交设计试验的固有应变法预测焊接变形不仅能够节省大量的计算时间,而且也能够获得较好的可靠性和准确性.

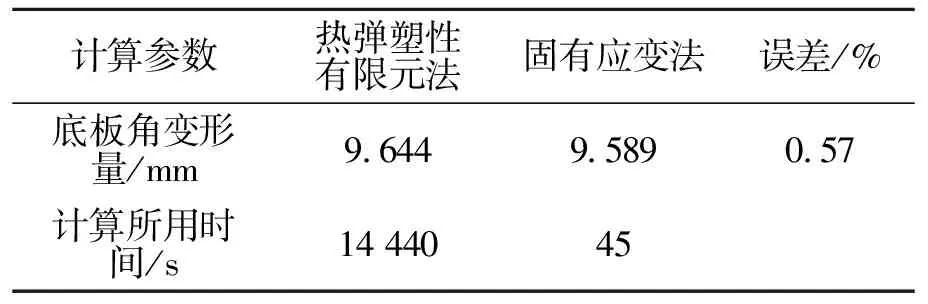
表4 热弹塑性有限元法和固有应变法计算的比较Table 4 Comparison between thermal elastic-plastic calculation and Inherent strain calculation

6 结论

1) 通过正交试验设计与数值模拟方法的结合,采用L9(34)正交表进行试验设计,共计9组试验,以位移差为评价指标,通过极差分析得出最优影响因子组合为K=0.8,L=0.8,U=0.65.

2) 通过变形云图和角变形曲线对比可以看出,热弹塑性和固有应变2种方法得到的焊接变形结果及角变形大小变化趋势基本一致,从而可以验证基于正交试验设计的固有应变法能体现焊接顺序、焊接方向对于焊接变形的影响.

3) 基于正交设计试验的固有应变法计算结果不仅可靠、准确，且能大大节省计算时间.

[1] 徐 琳,余昌莲,周旭春,等. 焊接变形预测的研究进展[J].机械工程师,2006,38(2): 27-29.

Xu Lin,Yu Changlian,Zhou Xuchun,et al.The research progress of welding distortion prediction[J].MechanicalEngineer,2006,38(2): 27-29. (in Chinese)

[2] 李鸿,任慧龙,曾骥,等. 预测船体分段焊接变形方法概述[J].船舶工程,2005(5): 56-58.

Li Hong,Ren Huilong,Zeng Ji,et al.General review of prediction methods of ships structures’ welding deformation[J].ShipEngineering,2005(5): 56-58. (in Chinese)

[3] Ueda Y,Murakawa H,Monhamed R A. Simulation of welding deformation for accurate ship assembling(report 1) in-plane deformation of butt welded plate[J].JournaloftheSocietyofNavalArchitectsofJapan,1992,171: 395-404.

[4] Ueda Y,Murakawa H,Monhamed R A. Simulation of welding deformation for accurate ship assembling(report 2) influence of initial imperfection to butt welded plate[J].JournaloftheSocietyofNavalArchitectsofJapan,1992,172: 559-566.

[5] Ueda Y,Murakawa H,Monhamed R A. Simulation of welding deformation for accurate ship assembling(report 3) out-of plate deformation of butt welded plate[J].JournaloftheSocietyofNavalArchitectsofJapan,1994,176: 341-350.

[6] Ueda Y,Murakawa H,Monhamed R A. Development of computer aided process planning system for plate bending by line-heating (report 4) decision making on heating condition,location,and direction[J].TheSocietyofNavalArchitectsofJapan,1994,174: 683-695.

[7] Jang C D,Lee C H,Ko D E. A study on prediction of deformation of plates due to line heating using a simplified thermal elasto-plastic analysis[J].JournalofShipProduction,1997,13(1): 22-27.

[8] Deng D,Murakawa H. Numerical simulation of welding distortion in large structures[J].ComputerMethodsinAppliedMechanicsandEngineering,2007,196: 4613-4627.

[9] Luo Y,Deng Dean,Xie Lei,et al. Prediction of deformation for large welded structures based on inherent strain[J].TransactionsofJWRI,2004,33(1): 65-70.

[10] 徐济进,陈立功,汪建华,等. 基于固有应变法筒体对接多道焊焊接变形的预测[J]. 焊接学报,2007,28(1): 77-79.

Xu Jijin,Chen Ligong,Wang Jianhua,et al. Prediction of distortion based on inherent strain method in multipass girth-butt welded pipes[J].TransactionsoftheChinaWeldingInstitution,2007,28(1): 77-79. (in Chinese)

[11] 魏天冬. T型构件焊接固有应变的研究及应用[D]. 河北:燕山大学,2011: 46-48.

[12] Deng D,Murakawa H,Liang W,et al. Prediction of welding distortion in a curved plate structure by means of elastic finite element method[J].JournalofMaterialsProcessingTechnology,2008,203(1/3): 252-266.

[13] 罗宇,鲁华益,谢雷,等. Tendon Force的概念及计算方法[J]. 造船技术,2004(4): 35-37.

Luo Yu,Lu Huayi,Xie Lei,et al. Concept and its computational method of Tendon Force[J].MarineTechnology,2004(4): 35-37. (in Chinese)

[14] 方洪渊. 焊接结构学[M]. 北京:机械工业出版社,2006:12-14.

[15] 张国栋,薛吉林,周昌玉. 基于正交试验设计的高温管道焊接工艺优化[J]. 焊接学报,2008,29(11): 54-56.

Zhang Guodong,Xue Jilin,Zhou Changyu. Optimization on welding procedure of high temperature pipeline based on orthogonal test design[J].TransactionsoftheChinaWeldingInstitution,2008,29(11): 54-56.(in Chinese)