基于小波变换的病灶心音信号识别

2013-11-19李丽胡方明

中国医疗设备 2013年2期

李丽，胡方明

西安电子科技大学生命科学技术学院，陕西西安 710071

0 前言

在我国，心血管疾病已对国民的健康造成了威胁，生活方式的转变不仅引发了高血脂、高血压、高血糖等危险因素，也使心血管疾病呈持续快速上升趋势，国家每年花费上千亿的经费用于心血管防治[1]。在心血管疾病诊断技术中，心音信号分析发挥着十分重要的作用[2]。通过心音诊断技术检测病灶信号可以实现无创诊断，及早发现疾病并做好早期治疗工作。

随着对小波变换的深入研究，小波变换应用日益广泛，在心音信号的提取和分析技术中起着重要的作用[3]。小波变换的优点是，能同时对信号时域和频域进行分析，具有良好的频域投射特点，因而能够将心音信号投射到不同尺度中进行能量分析。目前，心音信号基于小波包变换的处理算法复杂度高、处理速度慢，且对硬件要求高，因而实用性不强。本文提出了一种基于小波多尺度分解和能量变换分析的方法，通过对比相应尺度上的正常心音信号和非正常心音信号，准确检测出病灶信号。本文采用的是计算复杂度低的算法，因此具有较高的检测效率和实用性。

1 方法原理图

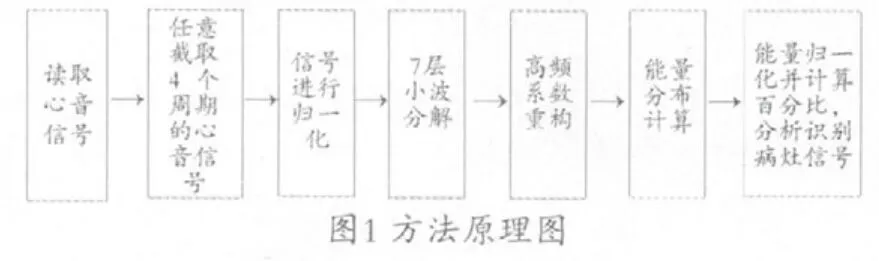
基于小波变换的病灶心音信号识别方法原理，见图1。本文首先读取4个周期长度的心音信号并进行小波变换，再将其投射到不同的频率段内，不同频率段信号代表不同的能量分布，计算每层的高频部分能量及分布，通过对比正常心音和非正常心音的分布来实现对病灶信号的识别。

2 心音信号提取

2.1 心音信号分析

正常心音包括4种成分，分别用S1、S2、S3、S4表示。正常情况下人工听诊能听到S1和S2，几乎听不到S3和S4。声音S1由二尖瓣和三尖瓣关闭产生，发生在心室收缩初期，是心室收缩期开始的标志。声音S2由主动脉瓣和肺动脉瓣的关闭产生，发生在心室舒张期，是心室舒张期开始的标志。一旦心脏功能出现异常，心音中将包含S1和S2以外的杂音，这些杂音的频率成分强度以及频率的分布都是研究的重点[4]。

通常心音的频域范围在 10～1000 Hz 之间，正常心音图，见图2。第一心音S1音调低，持续时间长，主要分布在中、低频范围，其波峰的低频范围为 10～50 Hz，中频范围为50～140 Hz。第二心音S2持续时间短，频率较高，在低、高频率范围内都有分布，其波峰的低频范围为 10～80 Hz，中频范围为 80～200 Hz，高频范围为 220～400 Hz[5]。

以前心脏疾病的诊断大部分是利用听诊器，个人主观因素对诊断结果影响很大，随着现在高灵敏传感器的使用和数字化处理技术的发展，利用心音信号进行疾病诊断更加客观和准确[6]。现代医学中利用小波变换的处理方式分析比较心音信号，使得心音诊断简单和准确。本文采用离散多尺度小波变换方法对截取的心音信号进行变换。

图2 正常心音图

2.2 离散小波变换

小波变换是信号处理领域中迅速发展的一个新领域，是傅里叶变换之后一个新的里程碑。与傅里叶变化和加窗傅里叶变化相比较，通过伸缩和平移对信号进行多分辨率的分析,很好地解决了时间分辨率和频率分辨率的矛盾[7]。小波变化分为连续小波变换和离散小波变换，在实际应用中，心音信号经过采集以后为离散的信号f（t），再结合离散小波变换特有的特点进行分析，小波ψa,b(t )变为：

离散小波变换定义为：

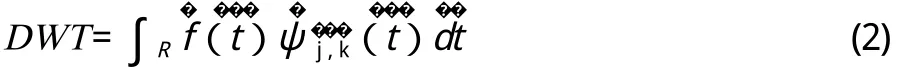
则心音信号通过的离散小波变换分解式为：

离散小波变化后的系数表示式为：

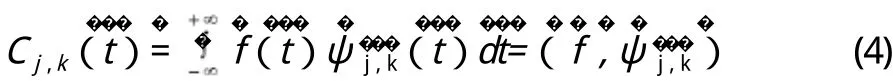
2.3 离散小波变换提取信号

在小波分析中，多分辨率分析是使用不同尺度的正交小波基对信号进行分解的，将信号分解到正交的不同频段上[8]。Daubechies小波为正交小波，也为双正交小波，并且为紧支撑，Φ(t)的支撑范围在t=0-(2N-l)，ψ(t)的支撑范围在(1-N)-N。小波ψ(t)具有N阶消失矩，ψ(Ω)在Ω=0处具有N阶零点。Daubechies小波db6的小波与尺度图形，见图3～4。

图3 db6的小波图形

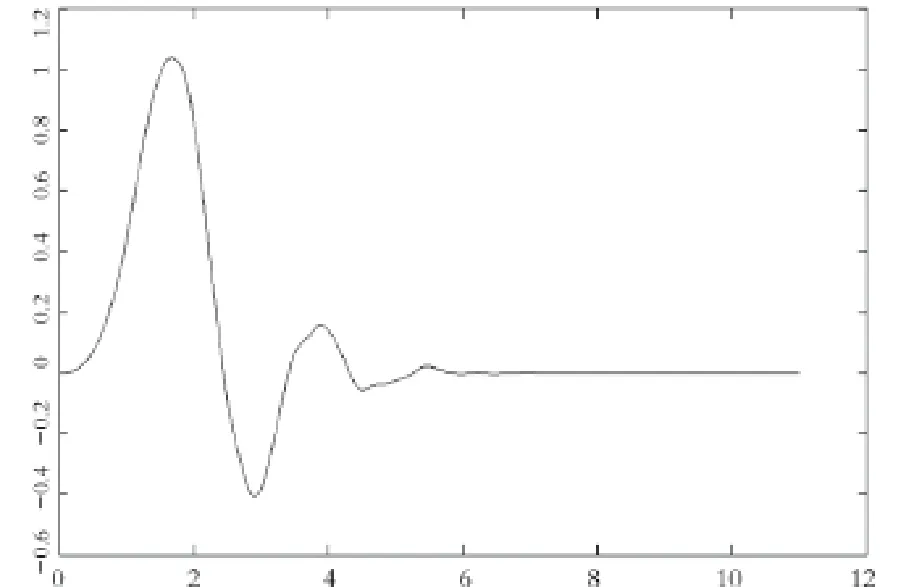
图4 db6尺度的图形

本文心音数据为教学用标准心音音频，其采样率为11025Hz，根据心音信号的特点，采用Dabbechies（db6）对心音信号进行7层分解，小波变换的空间划分示意图，见图5；离散小波变换的分解示意图，见图6。

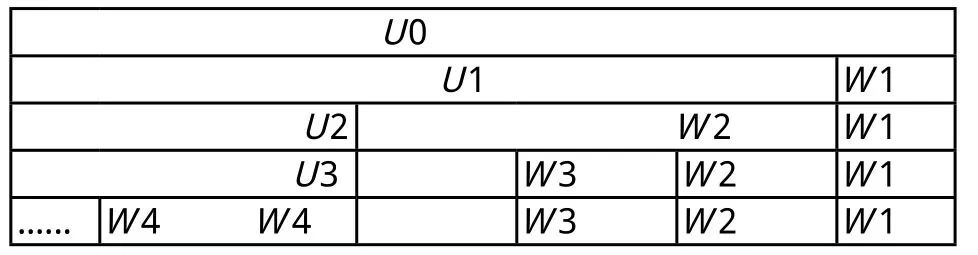
图5 小波变换的空间划分示意图

图6 离散小波变换的分解示意图

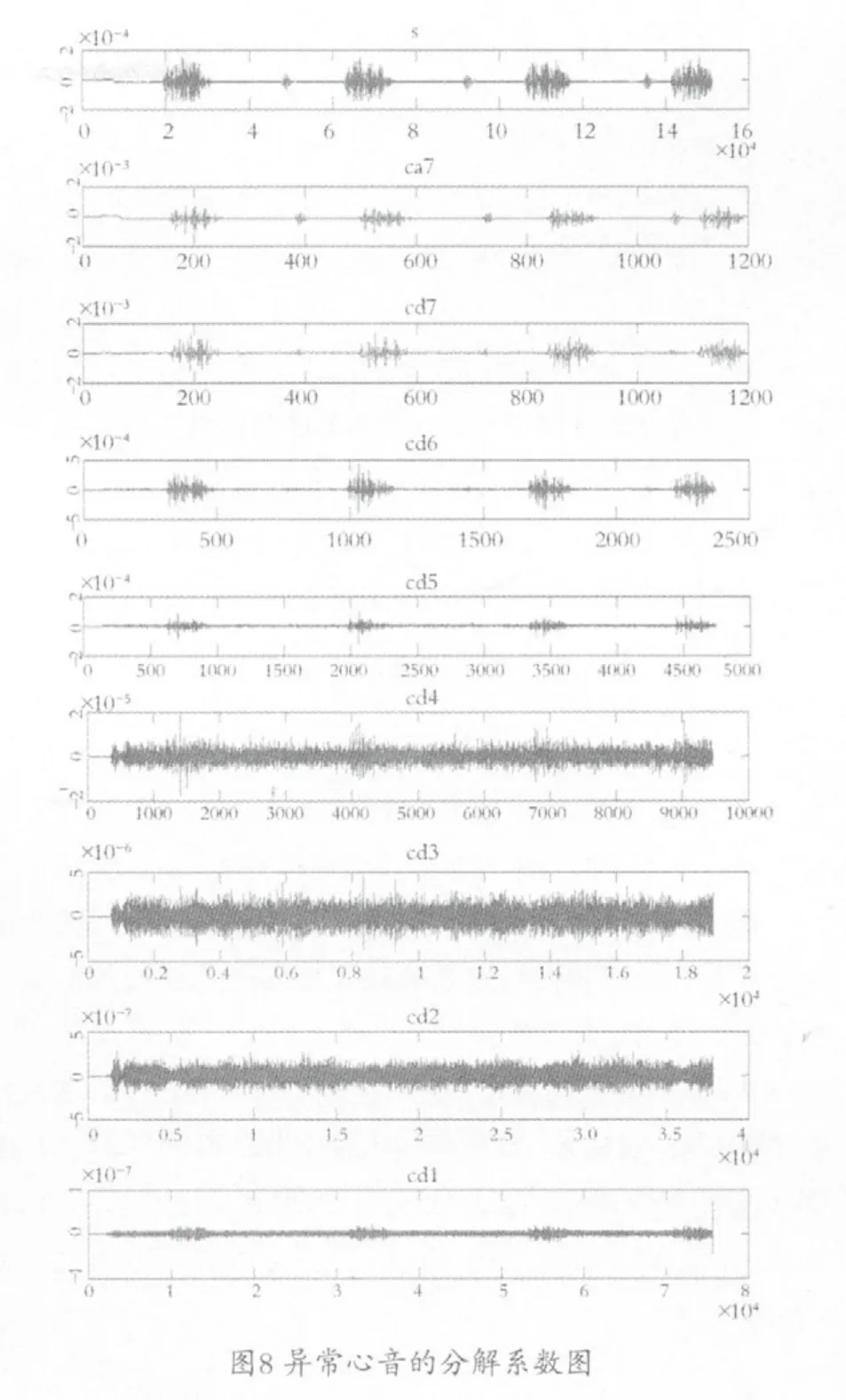
计算出每层的高频系数后，再根据心因信号的特点确定分解层数。本文仿真实验中，对心音进行7层分解，正常心音信号和异常心音的7层系数分布图，见图7～8。

从图中可以看出，噪声信号主要集中在cd1～cd4中，信号的部分能量也在其中。在5～7层中主要分布信号的能量，可以明显地看到心音信号能量的分布特点。

3 能量提取与数据分析

3.1 小波重构每层的高频能量处理

本文通过大量的仿真实验发现，病灶信号的异常能量主要集中分布在4～7层，具体算法步骤如下。

（1）计算每层的细节系数。本文中L=7，L为层数，利用小波基函数对截取的心音信号进行分解和重构。从前3层中可以看出主要集中的是外界的高频噪声，在第4～7层中病灶信号和正常信号的波形发生变化。

（2）对高频系数重构后计算每层能量。能量和信号之间相关性是信号识别最为重要的两个判断指标，由于外界噪声的影响，数据间的相关性发生较大的变化[9]。因此本文采用能量作为病灶信号的判断指标。

（3）计算每层能量在总能量中的比重。对能量进行归一化处理，以减少噪声对系统算法造成的影响，能量直方图，见图9～10；能量趋势图，见图11～12。

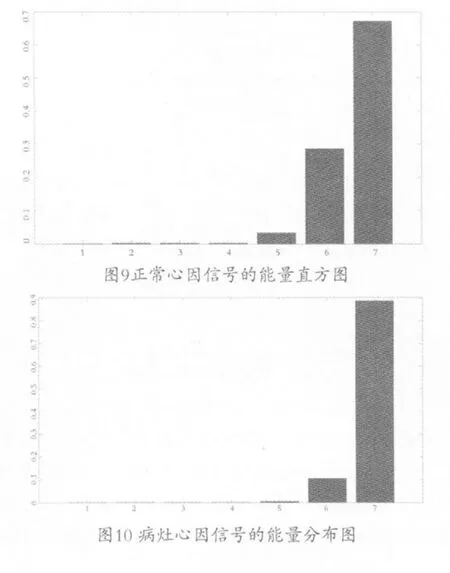
通过直方图，可以很直观地看到能量心音信号的能量分布特点，而趋势图可以明确地观察到不同心音的能量分布趋势，直观并且方便。

（4）进行能量的对比。进行能量的对比可以更好地区分正常和病灶心音信号，正常和病灶信号能量对比分布图，见图13。；加噪声之后的心音能量分布图，见图14。

由图13可以看出，正常和病灶心音可以被直接反映出来，通过计算能量特征向量的相关系数p，可以得出其相关性处于（0～0.97）之间，大量的实验证明其相关系数处于这个范围内便可检测为病灶信号，并且其检测率为98%，因此，本文提出的算法可以取得很理想的结果。由图14可以看出，加噪声和没加噪声的正常心音的能量分布图基本没有发生变化，因而得出结论：算法对于随机噪声就有良好的抗噪能力。这是本算法突出的优点。

3.2 仿真结果分析

在能量分析对比图中，可以看到病灶信号和正常心音信号，在前3层并没有很大的变化，这是由于前端传感器系统的噪声，表现为高频，叠加在任何信号上，因此在小波分解后前3层能量起伏变化很小；在4～7层中信号的能量大小发生较大的变化，通过病灶信号与正常信号的对比，说明病灶信号在4～7层的频率范围内能量与正常信号的能量有很大的差异，对比分析后可以准确的识别出病灶信号。本文通过大量的仿真可以得出本算法的识别率可以达到98%以上，具有很好的实用性。本算法还具有一定的抗噪能力，对环境的要求较低，实用性很强，且算法快速准确，适合应用于开发心音检测方面的便携式医疗器械。