水火弯板温度场理论分析和数值模拟
2013-11-18徐维铮郑卫刚
徐维铮 郑卫刚
(1.武汉理工大学交通学院,武汉 430063;2.武汉理工大学工程实训中心,武汉 430063)
水火弯板也称为线状加热冷却成形,即利用钢板局部受高温冷却后产生的局部热弹塑性变形而达到钢板整体的弯曲变形,属于温度场和变形场耦合的三维瞬态热弹塑性力学问题。水火弯板变形主要由温度场决定,对钢板温度场进行合理有效的分析至关重要。水火弯板温度场的研究方法主要有解析法、实验法和数值模拟法。在前人研究的基础上,本文通过理论分析结合数值模拟系统分析了水火弯板温度场。
1 高斯分布热流密度模型
高斯分布的热流密度模型见图1。
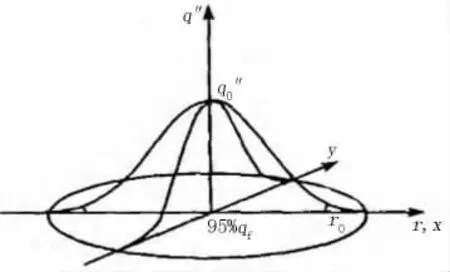
图1 高斯分布的热流密度模型Figure 1 Heat flux density model of Gauss dist ribution
在水火弯板的过程中,焊炬喷出的冲击射流是通过一定的作用面积给钢板加热的,这个作用面积称为加热斑点。加热斑点上的热量分布是不均匀的,中心多而边缘少。费里德曼将加热斑点上热流密度的分布近似地用高斯数学模型来描述,距加热中心任意点的热流密度可表示为如下形式:
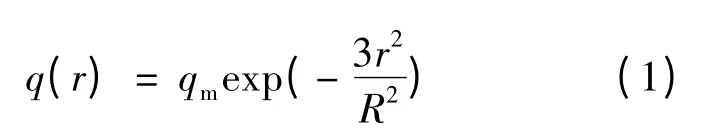
式中 qm——加热斑点中心的最大热流密度;
R——热源有效加热半径;
r——A 点距离焊炬加热斑点中心的距离。
对于移动热源:

qm的计算可以通过热流密度在整个加热区域上的积分等于总热输入量的条件来求。
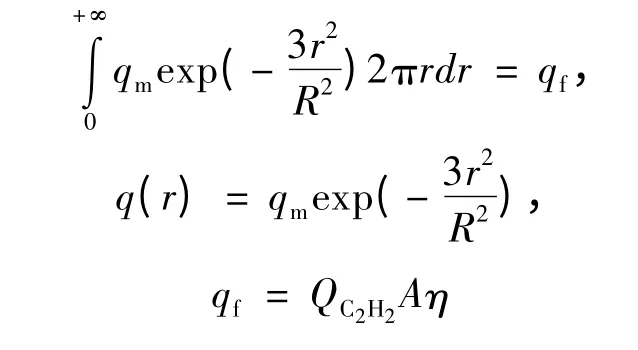
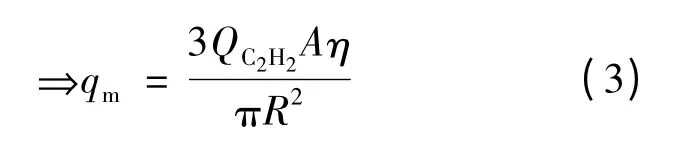
2 高斯分布热源模型的计算案例
2.1 参数列表
模拟样板的参数见表1。
2.2 高斯分布热流密度模拟图
高斯分布热流密度模拟图见图2。
3 钢板温度场的理论分析
3.1 微元六面体分析法
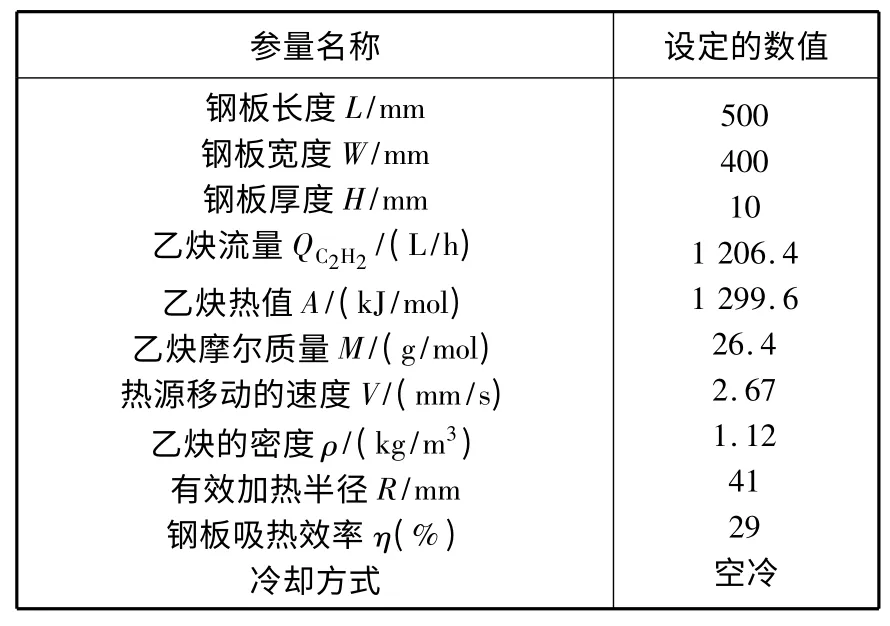
表1 模拟参数列表Table 1 List of numerical reference
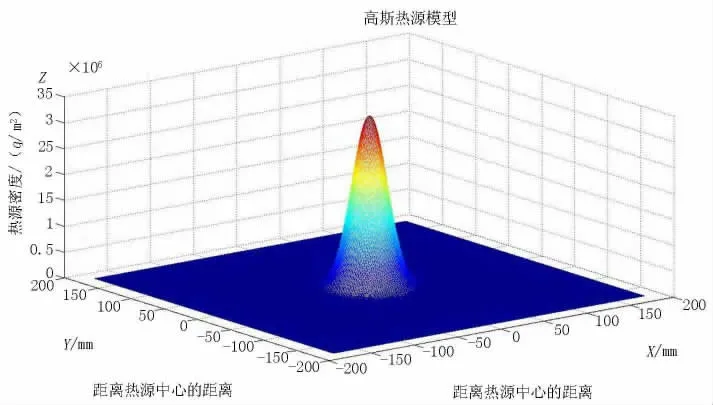
图2 高斯分布热流密度模拟图Figure 2 Simulative diagram of Gauss distribution heat flux density
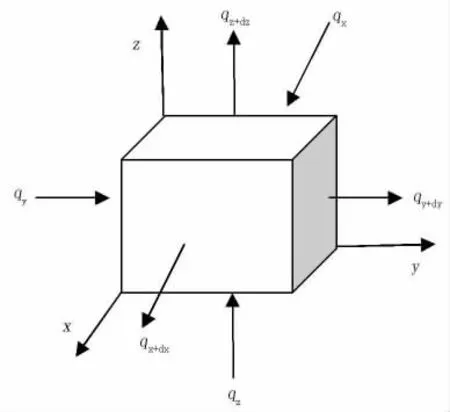
图3 微元六面体Figure 3 Micro hexahedron
图3 为微元六面体。在无内热源产生的情况下,净进入该微元六面体内的总热量等于该微元控制体内温度升高所吸收的总热量。
x 方向单位时间内净进入的热量:
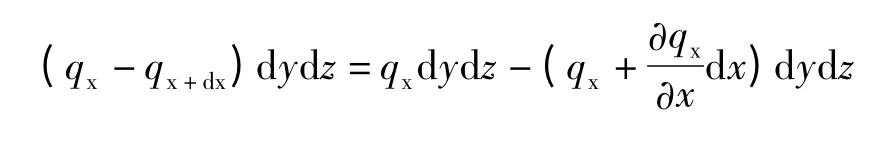
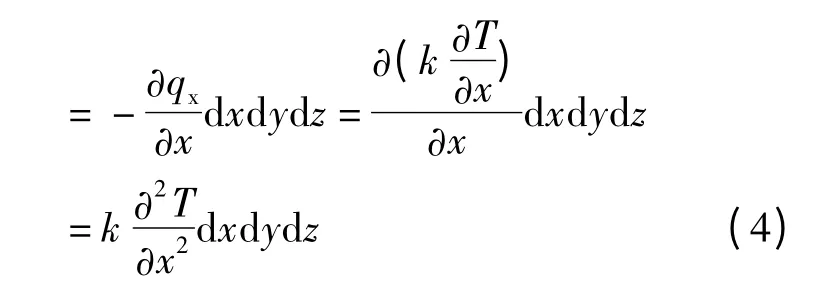
y 方向单位时间内净进入的热量:
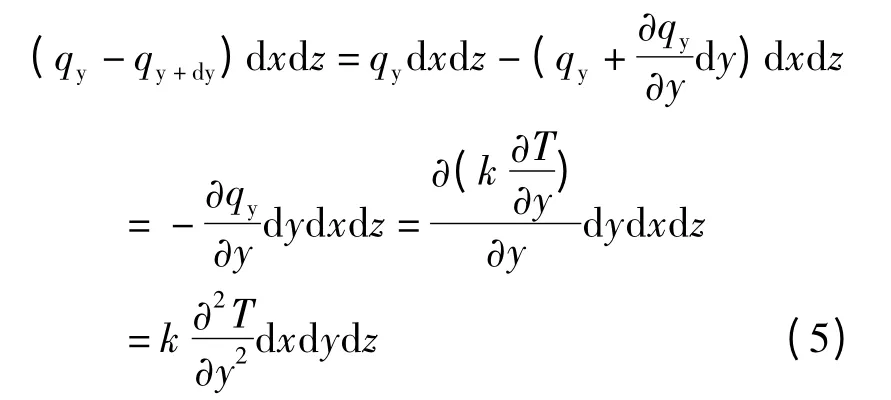
z 方向单位时间内净进入的热量:
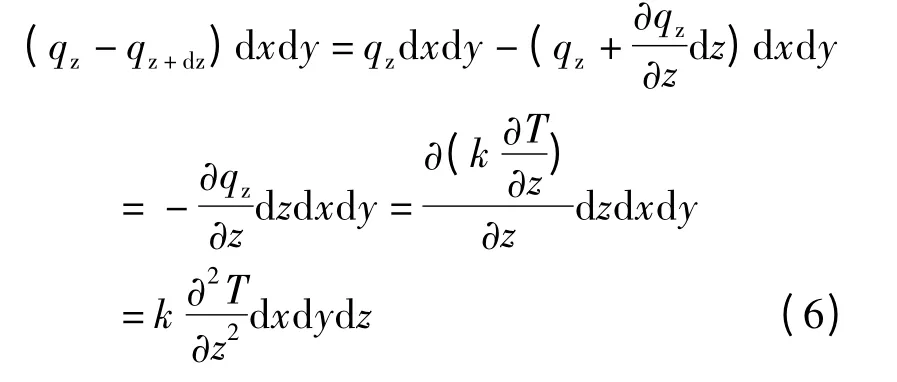
单位时间内净进入微元六面体的总热量:
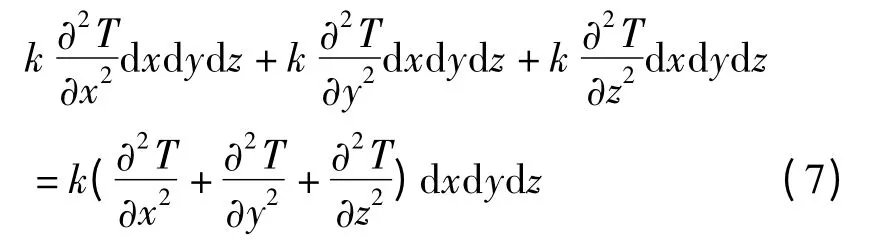
单位时间时间内微元控制体温度升高所需吸收的热量为:
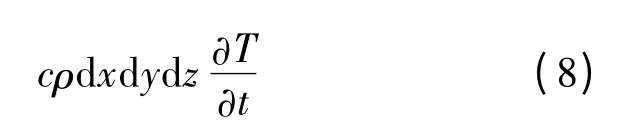
由热量守恒可得:
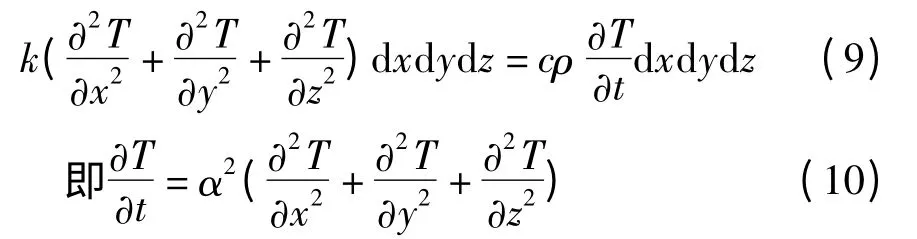
从理论上来说,给定初始条件和边界条件,可以求解上面的非线性二阶偏微分方程。求得的解析解就是钢板的温度场T(x,y,z,t),然而由于现有的数学工具还不能求得上述问题的精确解。
3.2 有限容积体分析法
通过上面的分析发现高斯热源模型不能解决对于一定氧乙炔流量的加热状况下,钢板变形的吸热效率是多少的问题。为了分析这个问题,从最基本的能量守恒原理出发,来推导钢板吸热效率的理论公式。由于钢板的上表面是直接受热面,因此我们在加热过程中的某一时刻t 取包含整个钢板的控制容积为研究对象(见图4)。
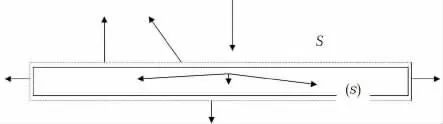
图4 钢板控制容积Figure 4 Steel plate control volume
(1)设dt 时间内热源输入给钢板表面的总热量为Qtot,dt 时间内通过钢板表面辐射出去的热量为Qrad,dt 时间内钢板表面通过与空气自然对流换热量为Qconv,dt 时间内钢板内部温度升高所需吸收的热量为Qabsorb。根据能量守恒,可得Qtot=Qrad+Qconv+Qabsorb。
(2)牛顿冷却公式:q=h(TS-T∞)。式中,h为对流换热系数;TS为钢板表面的温度;T∞为环境的温度。
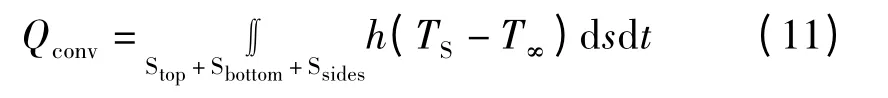
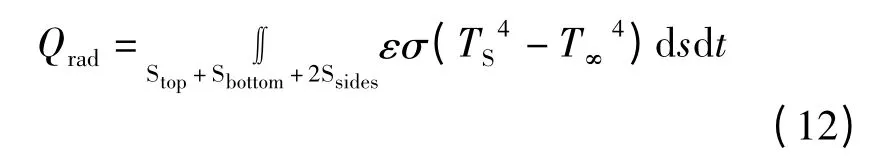
(4)钢板净吸收的热量使其内部的温度升高,在时间间隔[t,t+dt]内,钢板内部各点的温度从T(x,y,z,t)变化到T(x,y,z,t+dt),则V 内钢板温度升高所需吸收的总热量
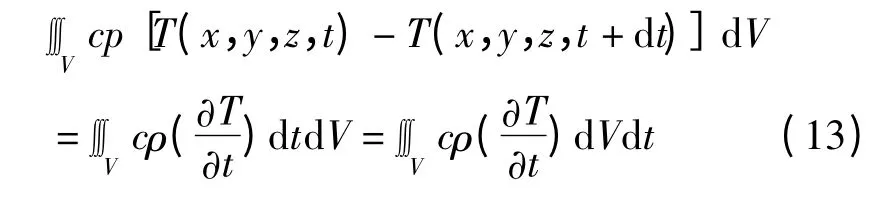
(5)净吸热效率:在钢板的加热过程中,设钢板沿着加热线运行的时间间隔为[t1,t2],则上面的各部分热量在不同的时刻都在变化,因此,将上面的各式对时间进行积分:
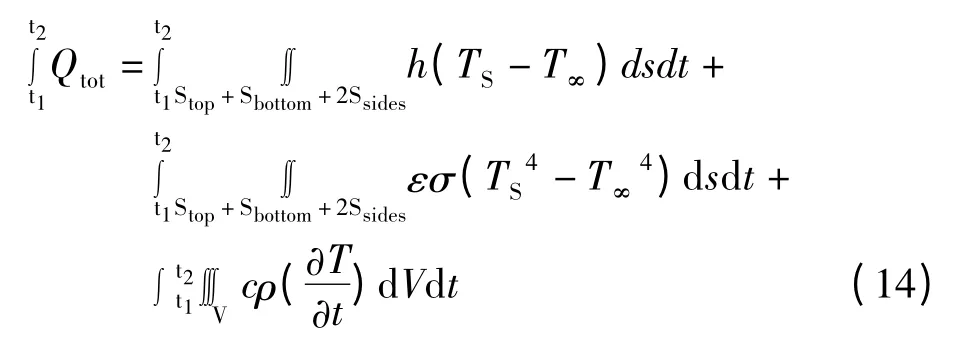
[t1,t2]时间内氧乙炔燃烧所放出的总热量:
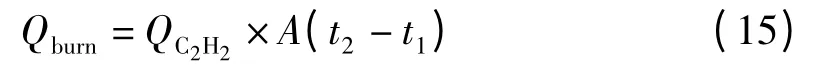
钢板的吸热效率:
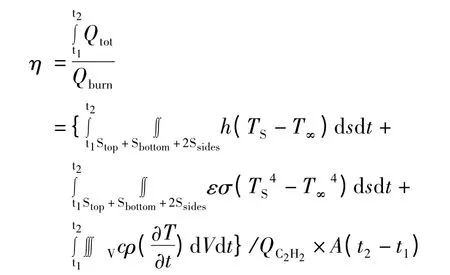
(6)要求解上式,需要知道钢板表面和钢板内部的温度场分布规律即TS(x,y,z,t)和Tin(x,y,z,t),以及相关的辐射和自然对流换热系数。
4 钢板表面温度场的ANSYS 模拟分析
4.1 实验模型的选取:
(1)温度区间的划分:为了提高计算精度,将钢板加热面划分为加热区、过渡区和平缓导热区三部分。实验和计算表明,水火弯板加工过程中,距离加热线100 mm 范围内的钢板温度变化相当剧烈,温度梯度大,当距离超过150 mm,钢板温度变化很小。因此,将加热区和过渡区建立在距加热线150 mm 范围内,其余区域为平缓导热区。
(2)材料参数的选取:进行水火弯板温度场分析必须确定的热物理性能参数有:导热系数λ(W/m2·℃)、对流换热系数β(W/m2·℃)、密度ρ(kg/m3)、比热容C(J/kg·℃)以及初始温度(℃)。在本数值模拟分析中,钢板的初始温度取为室温,即30℃。材料的热物理性能参数见表2。
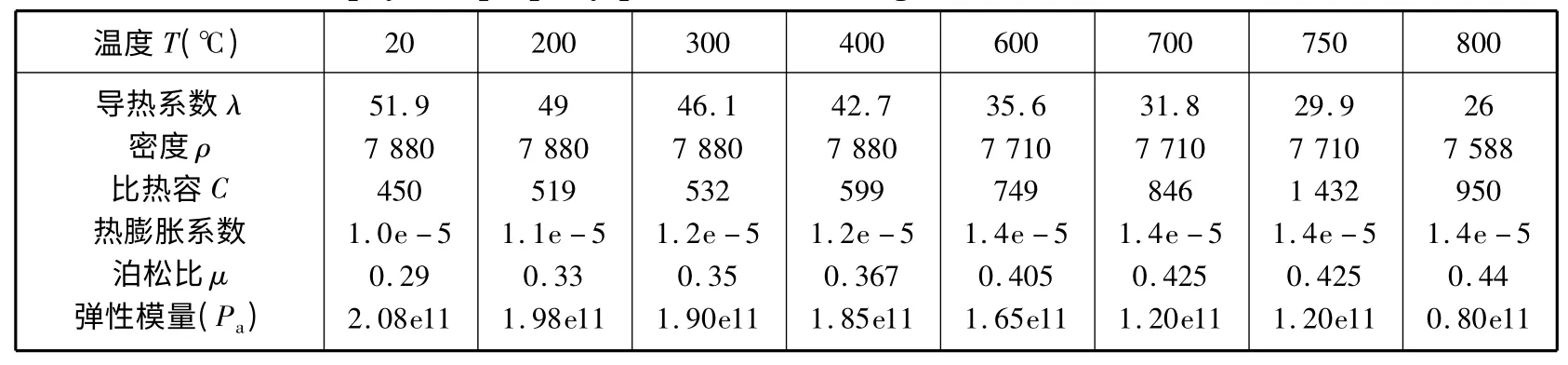
表2 普通船用低碳钢材料的热物性参数列表Table 2 Thermophysical property parameters list of geneal marine low carbon-steel material
(3)单元的选择:根据上述的原则,加热区和平缓导热区选用8 节点的70 号六面体单元,过渡区选用10 节点的87 号四面体单元。为了使热源热流加载到加热区的体单元,还需要建立一个用于承载热源热流的面,称其为载流面,将载流面紧铺于加热区上表面,载流面选用8 节点的152 号表面效应单元。
(4)热源的加载:利用ANSYS 软件的函数加载功能,在每个载荷步内,以热源中心点(a,b)为中心,按高斯热源的变化面上加载,随着热源的移动每个载荷步内的(a,b)也相应的改变,这样通过控制(a,b),使其随时间变化,也就是随载荷步变化,就可以模拟热源的移动。
4.2 表1 样板的网格划分
将表1 所示的模拟样板进行网格划分,见图5。

图5 样板网格的划分Figure 5 Grid division of templet
取热源的起点为全体笛卡尔坐标系的原点(0,0,0),热源沿加热线所沿y 轴方向移动,所以加工钢板表面在不同的时刻各点距热源中心距离为
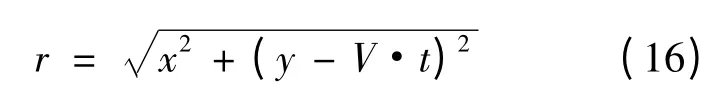
式中,V 为热源移动速度(mm/s),t 为热源移动的时间(s)。然后加载热源(冷却方式为空冷),设定初始条件,边界条件和载荷步,通过ANSYS 求解器P0ST1 求解,利用后处理器POST26 和时间历程处理器分析得到图6~图9 所示的温度场分布云图和拟合温度曲线。

图6 147 s 时钢板表面的温度场分布云图Figure 6 Temperature field distribution cloud chart on the surface of steel plate as 147 s
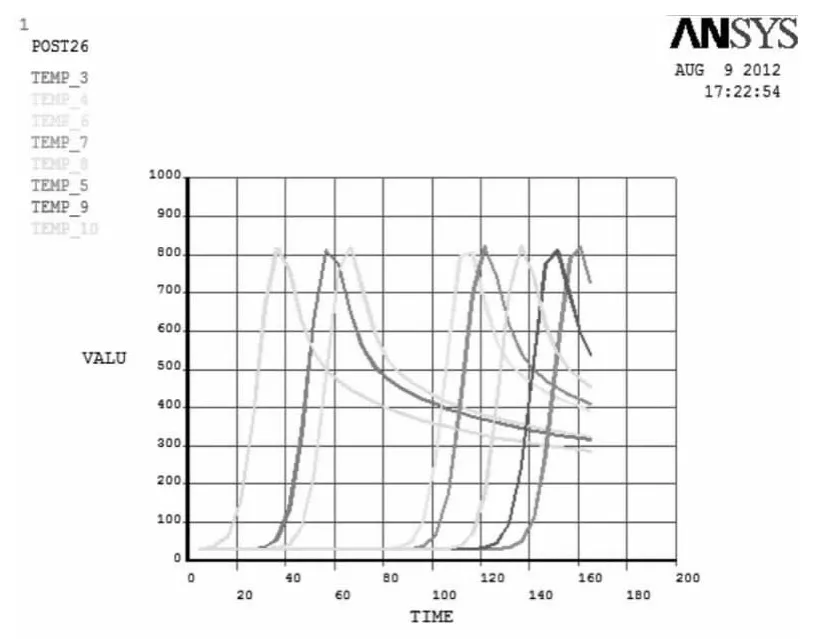
图7 钢板加热线上不同点温度随时间变化的的分布曲线Figure 7 Distribution curves of various points temperature according to time changed on steel plate heating path
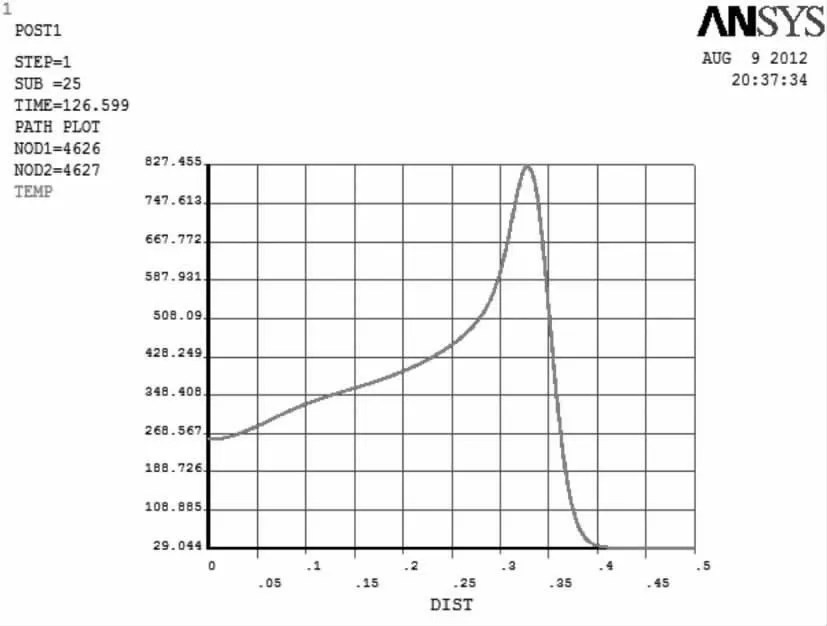
图8 钢板上表面沿加热线方向温度分布曲线Figure 8 Temperature distribution curve along heating path direction of steel plate top surface
5 结束语
(1)通过分析,对水火弯板过程中钢板表面吸热和温度变化机理有了更清晰的认识,为更加有效合理的加热钢板提供参考。
(2)高斯热源热流密度模型来源于对焊接温度场的研究,其优点是用热流密度的概念近似地描述了焊炬加热钢板过程中冲击射流火焰对钢板输入热流的宏观过程。该模型同时考虑到了实际加热过程中对流换热和辐射换热。其缺点是在进行数值模拟计算的时候,需要知道某一氧乙炔流量下的有效加热半径R,以及对钢板加热的效率η。而这两者即使进行试验测量也很困难。因此建立更有效合理的数学模型来描述钢板吸热的机理将更有现实意义。
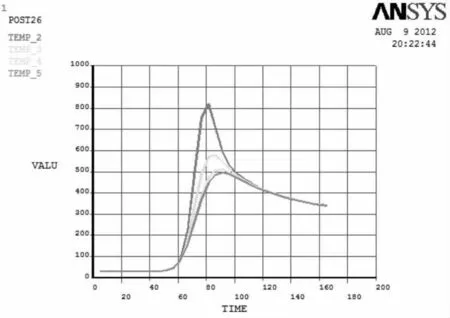
图9 沿厚度方向同一条线上的四个点的温度随时间变化曲线Figure 9 Four points temperature curves of same line along thickness direction as time changed
[1]H.H.雷卡林,著.徐碧宇,庄鸿寿,译.焊接热过程计算.北京:中国工业出版社,1958.
[2]D.拉达伊,著.熊第京,郑朝云,史耀武,译.焊接热效应——温度场、残余应力、变形.北京:机械工业出版社,1997.
[3]董大栓.水火弯板成形规律及加工参数的确定研究:[学位论文].上海:上海交通大学.2002.
[4]董大栓,柳存根,谭家华.水火弯板计算中高斯分布热源模型各参数的实验确定.上海交通大学学报,2001,35(10):1459.
