MCMC粒子滤波的GPS定位数据处理算法

王尔申 蔡 明 庞 涛

（沈阳航空航天大学电子信息工程学院，沈阳，110136）

引 言

目前，全球定位系统（Global positioning system，GPS）在军事和民用方面均得到了越来越广泛的应用。比如在汽车和船舰导航、交通管理、车辆监控、警车指挥、航空摄影、海洋捕捞作业和农业工程等应用领域，目前多采用动态单点式的GPS接收机或嵌入式单点GPS原始制造商（Original equipment manufacture，OEM）模块进行定位。动态单点定位方式在选择可用性（Selective availability，SA）政策取消后，其圆概率误差（Circular error probable，CEP）定位精度在理想情况下一般能达到10m左右。而在实际中，卫星的分布情况、天气情况、地理位置、接收机和天线等引入的系统误差的影响等都可能产生更大的误差值。尤其是在城市环境中，受到多径效应的影响，观测误差服从的分布不是严格的高斯分布［1］。另外，在GPS的技术指标中通常给定的是CEP误差值，因此对个别测量值的误差值达到几十米也并不少见。为了平滑定位输出数据，常用的滤波技术有卡尔曼滤波（Kalman filtering，KF）、扩展卡尔曼滤波（Extended Kalman filtering，EKF）和无迹卡尔曼滤波（Unscented Kalman filtering，UKF）等。这些算法均要求观测噪声和过程噪声为独立不相关的高斯白噪声，不能对非高斯的误差进行修正处理［2－3］。而粒子滤波（Particle filter，PF）算法作为一种非线性滤波方法，可以克服上述缺点，随着采样粒子数的增大，逐渐趋向状态的后验概率密度，在解决非高斯误差问题时具有明显的优势。因此，在处理非线性非高斯问题时得到了广泛应用，如：卫星系统姿态估计、目标跟踪等［4－6］。目前粒子滤波算法在GPS导航定位数据处理中也获得了广泛应用，将粒子滤波用于动态单点定位、高动态定位中等［7－8］，但在精确度方面仍可改善，抑制粒子退化是方法之一。

文中首先介绍粒子滤波的原理，接着详细地对马尔可夫链蒙特卡罗（Markov chain Monte Carol，MCMC）粒子滤波进行分析，给出所建立的系统动态状态空间模型与观测模型。结合实例与基本PF进行比较，实验结果表明：MCMC粒子滤波算法能有效降低GPS定位位置和速度误差，其滤波性能优于基本PF算法。

1 MCMC粒子滤波算法描述

PF是一种基于蒙特卡罗模拟和递推贝叶斯估计的滤波方法。Gordon提出基于蒙特卡罗方法的序贯重要性重采样PF算法以来，PF成为非线性非高斯系统状态估计问题的一个研究热点，广泛用于自动控制、机器人技术、统计信号处理等研究领域［9］。

假设描述动态系统的状态方程和观测方程为

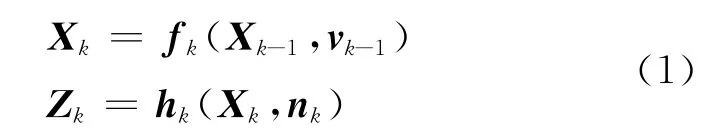
式中：Xk为状态向量，Zk为测量向量，fk为状态转移函数，hk为状态向量和观测向量之间的传递函数，vk－1为系统噪声，nk为观测噪声。

1.1 基于序贯重点采样的粒子滤波

PF的核心思想是利用有限个随机采样样本（这些样本被称为“粒子”）的加权和来近似表示状态变量的后验概率分布，从而得到状态的估计值［10］。

设k－1时刻有一组后验粒子集｛xk－1（i），ωk－1（i）；i＝1，2，…，N｝，其中N为粒子数目，xk－1（i）为k－1时刻的第i个粒子，ωk－1（i）为k－1时刻第i个粒子的权重。

（1）粒子集初始化，k＝0：

根据先验概率密度p（X0）抽取随机样本，为随机样本数）。

（2）当k＝1，2，…时，执行以下步骤：

（a）状态预测

根据系统的状态方程抽取k时刻的先验粒子：｛Xk｜k－1（i）；i＝1，2，…，N｝～p（Xk｜Xk－1）。

（b）更新

首先，进行权值更新。在获得测量值之后，根据系统的观测方程并利用式（2）计算粒子的权值

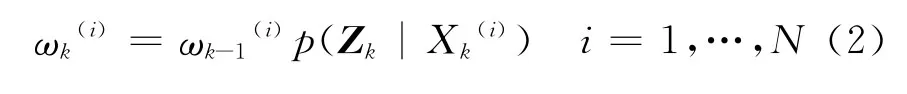
归一化权值为

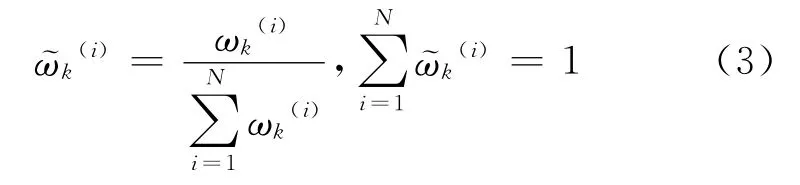
然后，计算有效粒子数，并与设定的阈值Nthres进行比较；如果＜Nthres，则对先验粒子集（Xk｜k－1（i））进行重采样，得到N个等权 值的粒子否则，执行下面的步骤。

（c）估计

计算当前时刻系统的状态估计值

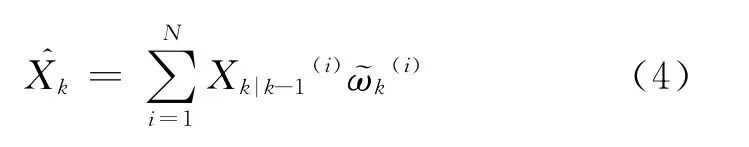
1.2 MCMC粒子滤波算法

PF的重采样抑制了权的退化，但也带来粒子不再独立，简单的收敛性结果不再成立，甚至会引起粒子贫化等问题。为此，对每个粒子引入MCMC移动步骤来解决粒子退化问题［11］。MCMC方法对每个服从后验概率的粒子实施核为的马尔可夫链变换，使得服从同样的概率密度，并且新的粒子已经移到不同的位置，分布更加合理，避免了粒子贫化问题。文中在PF基本算法基础中引入 Metropolis Hastings（M－H）抽样方法。具体过程为：

（1）从区间［0，1］按照均匀概率分布抽样得到门限值u，u～U［0，1］。

2 基于粒子滤波的GPS定位数据处理

由于GPS信号是视距传播，GPS信号易受到建筑物及树木等物体的遮挡，此时，GPS接收机定位误差将变大或者无法进行定位，降低了定位数据的可用性，加上GPS信号受地面反射的多径信号影响，都将引起定位误差变大，造成其在应用过程中定位偏离真实位置的问题，GPS的定位精度一般在10m以内，但有时定位误差会更大［12］。为此，引入PF算法对GPS数据进行处理，改善GPS定位效果。

2.1 运动状态的描述与状态方程

GPS接收机输出的参数包括经度、纬度、速度、方向角等信息。根据距离、速度以及加速度之间的关系，列出系统状态方程和系统输出方程。

选取状态变量为X＝ ［xE，vE，aE，xN，vN，aN］T，其中，xE，xN分别为运动载体东向和北向的位置分量；vE和vN分别为运动载体东向和北向的速度分量；aE和aN分别为运动载体东向和北向的加速度分量。则系统的状态方程为

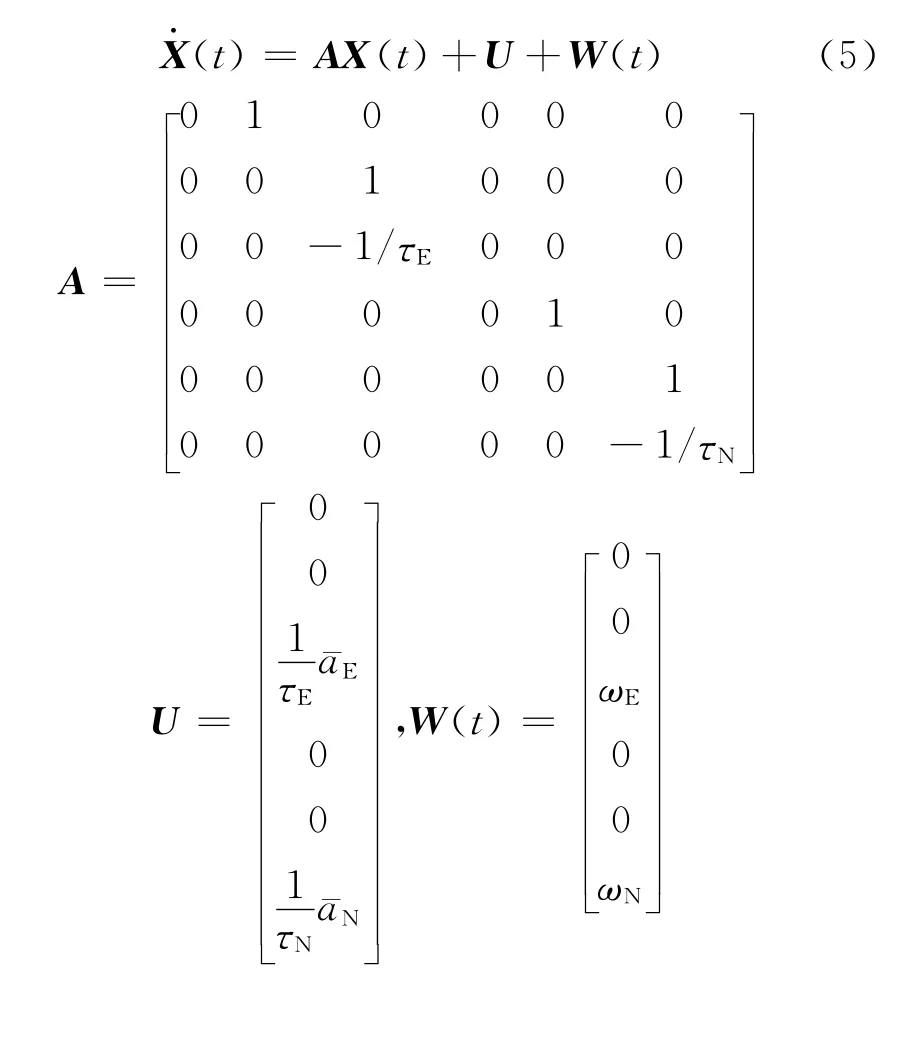
式中：ωE，ωN分别为的高斯白噪声；τE，τN分别为运动载体东向和北向的机动加速度变化率的相关时间常数分别为运动载体的东向和北向机动加速度分量的当前均值。

2.2 观测方程

将GPS接收机输出的东向位置信息zE、北向位置信息zN、速度v以及方向角θ作为观测量，即则，观测量和状态变量之间的关系如下

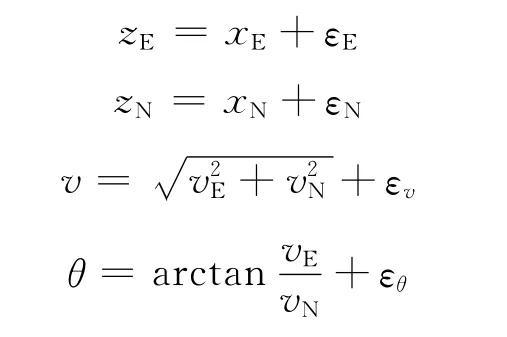
于是，系统的观测方程为

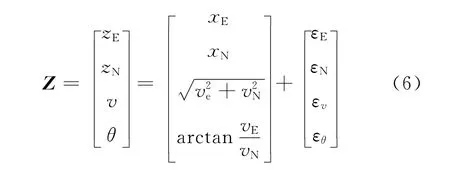
式中：εE，εN分别是GPS接收机输出的东向位置和北向位置的观测噪声，可近似为（0，σ2E），（0，σ2N）的高斯白噪声；εv，εθ为接收机输出的速度和方向角的观测噪声，可近似为（0，σ2v），（0，σ2θ）的高斯白噪声。

2.3 基于MCMC粒子滤波的GPS定位数据处理算法

PF用于GPS定位数据处理的算法描述为：

设k－1时刻有一组后验粒子集为｛xk－1（i），ωk－1（i）：i＝1，2，…，N｝，其中N为粒子数目，xk－1（i）为k－1时刻的第i个粒子，ωk－1（i）为k－1时刻第i个粒子的权重。

（1）粒子集初始化，k＝0：

在初始值X0点（载体的初始位置：东经123°24.15436′、北纬41°55.53523′），根据先验概率密度产生N个粒子，得到粒子集并设置初始化权值为ω0（i）＝1／N。

（2）Fork＝1，2，…执行以下步骤：

①状态预测根据系统的状态方程抽取k时刻的先验粒子｛Xk｜k－1（i）：i＝1，2，…，N｝～p（Xk｜Xk－1）。

②更新

（a）权值更新 在获得测量值之后，根据系统的观测方程并利用式（7）计算粒子的权值

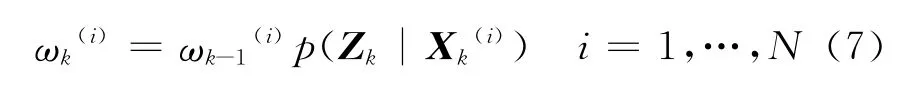
归一化权值为

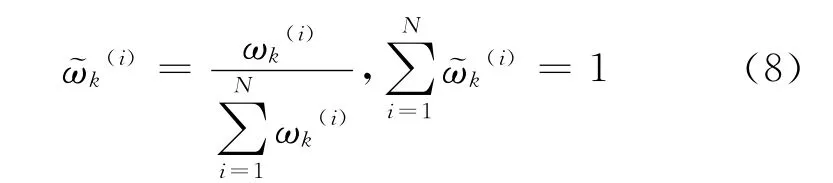
（c）M－H抽样利用 MCMC方法对（b）中得到的粒子进行M－H采样，得到新的粒子集｛，1／N；i＝1，…N｝

③估计计算当前时刻系统的状态估计值

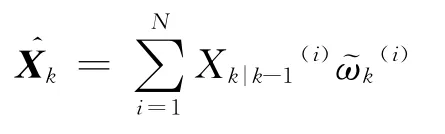
3 实测实验与结果分析

3.1 实验条件

利用 U－BLOX公司的RCB－4HGPS接收机作为实验数据采集设备，在沈阳航空航天大学操场绕椭圆形跑道一圈，采集的数据包括经度、纬度、速度、方向角等。采样频率设置为最大更新率4Hz，GPS接收机初始位置为东经123°24.154 36′、北纬41°55.535 23′、初始速度为0，方向角为164.22°，采集数据时间为5min。RCB－4H型GPS接收机，其定位精度为2.5m（CEP）。

3.2 实验数据处理与结果分析

首先对所采集到的经纬度数据进行预处理。由于实验中GPS数据采集系统移动范围相对较小，获取的位置经度和纬度数值仅以分的小数部分发生变化，而其度和分的整数部分不变。为此，为了使实验的结果更加直观，方便程序计算，对采集到位置的经度和纬度数据进行如下处理，具体为：去除经纬度数据中小数点前面的数据位，将小数点后面的数据扩大1 000倍。速度单位转换为m／s。如：其中一组数据为：经度为123°24.154 36′，纬度为41°55.535 23′，速度为1.046节／s，方向角为164.22°。预处理后数据为：经度154.36×10－3，纬度535.23×10－3，速度 0.538 1m／s，方向角164.22°。其他数据做类似的处理，不再赘述。

将采集到的数据作为实验数据，对这些数据分别利用文中1.1节的PF和MCMC粒子滤波进行处理，得到结果如图1所示。

图1中横轴为经度，纵轴为纬度，单位10－3′。图中，a点所示为运动的初始位置，b点附近由于操场看台遮阳棚的遮挡，数据采集平台未正常接收到GPS定位数据，故图中量测状态曲线在b点附近出现间断，PF和MCMC粒子滤波依然可以给出状态估计，说明在没有量测数据可利用的情况下，利用PF算法也可以根据以前的经验对状态X作出估计。但从图1可以明显看出，MCMC粒子滤波对状态的估计性能要优于基本PF。两种算法处理后的不同参数如表1所示。

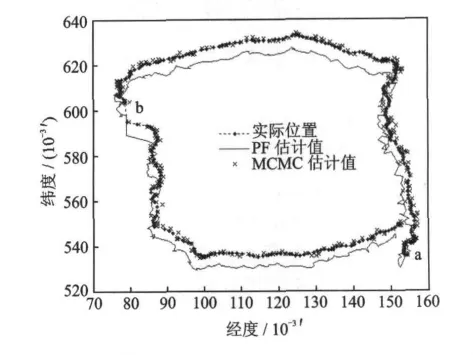
图1 MCMC粒子滤波和PF的结果对比

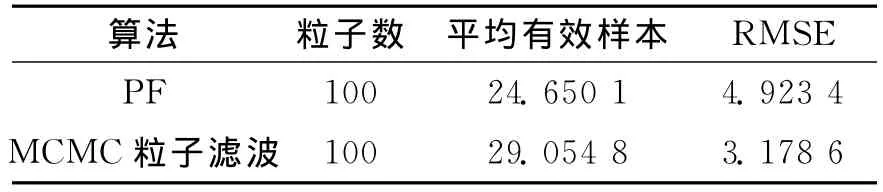
表1 采用不同算法处理后的参数比较

如表1所示，粒子数目同为N＝100，且过程噪声方差Q＝5、量测噪声方差R＝1时，MCMC粒子滤波算法的RMSE＝3.178 6，基本PF算法的RMSE＝4.923 4，说明 MCMC粒子滤波比基本PF算法估计精度高。此时，MCMC粒子滤波的有效样本为29.054 8，PF为24.650 1，说明 MCMC粒子滤波比基本PF更能有效地抑制样本退化，而且，在同等条件下，有效样本越多，估计精度越高。MCMC粒子滤波和基本PF在定位经纬度和速度的估计误差对比曲线如图2～5所示。

图2，3为PF的经度和纬度的估计误差对比曲线。图中横轴为时间，单位为s，纵轴为经度误差，单位为10－3′。图4和图5横轴为时间，单位为s，纵轴分别为东向速度误差和北向速度误差，单位为 m／s。

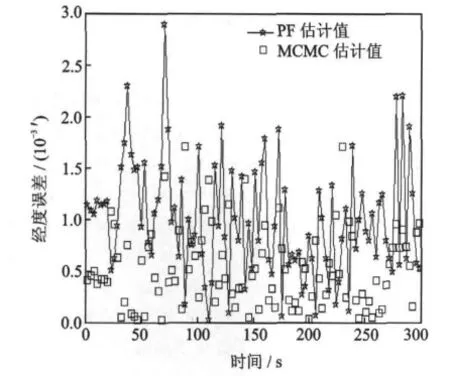
图2 MCMC粒子滤波和PF算法经度估计误差对比

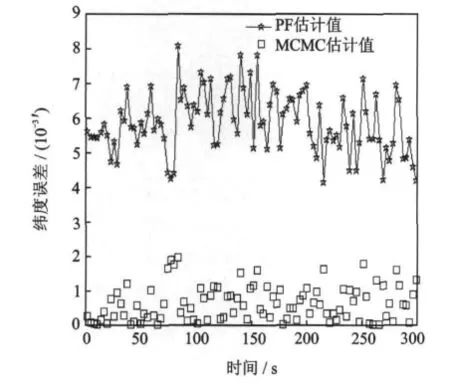
图3 MCMC粒子滤波和PF算法纬度估计误差对比

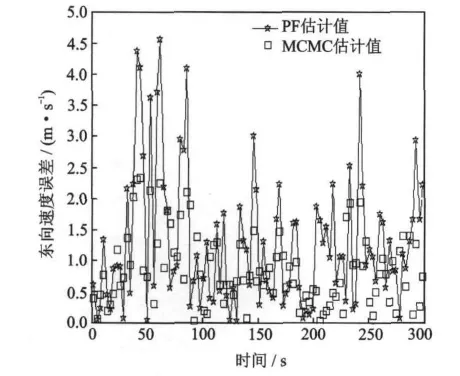
图4 MCMC粒子滤波和PF算法东向速度估计误差对比

从图2～5可知，MCMC粒子滤波算法在GPS定位的经纬度和速度的处理效果方面要优于基本PF，提高了GPS定位数据参数的可用性。该算法实现中的参变量不需要其他辅助设备，可用于汽车、轮船、航空等运动载体定位数据的滤波处理。

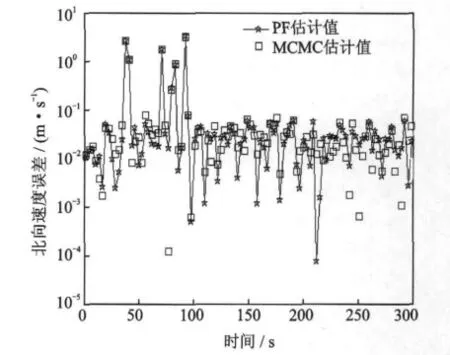
图5 MCMC粒子滤波和PF算法北向速度估计误差对比

4 结束语

将MCMC粒子滤波算法应用于GPS定位数据处理问题中，解决了PF算法在粒子抽样过程中粒子退化问题，提高了对接收机定位状态的估计精度。通过建立动态状态空间模型，利用GPS数据采集设备获取的实验数据分别对PF算法和MCMC粒子滤波算法的滤波效果进行了实验验证，结果表明MCMC粒子滤波可以有效地抑制样本退化，其滤波效果优于PF，提高了GPS定位数据处理的效果。同时，在GPS信号质量较差或者短时无法定位时，MCMC滤波算法作为一种辅助方案为系统提供了较准确的导航定位数据。本研究的实验表明MCMC粒子滤波算法在GPS定位数据处理和改善定位状况方面是可用的且有效的。

［1］Sayim I，Pervan B，Pullen S，et al.Experimental and theoretical results on the LAAS sigma overbound［C］／／Proceedings of the ION GPS.Portland，Oregon：［s.n.］，2002：29－38.

［2］Mojtaba Bahrami，Marek Ziebart.A Kalman filter based Dopper－smoothing of code pseudoranges in GNSS challenged environments［C］／／Proceedings of the ION GNSS 2011.Portland：［s.n.］，2011：1－11.

［3］Zhou Junchuan，Yang Yuhong，Zhang Jieying，et al.Applying quaternion－based unscented particle filter on INS／GPS with field experiments［C］／／Proceedings of the ION GNSS 2011.Portland：［s.n.］，2011：1－14.

［4］吴海亮，王惠南，陈志明，等.基于粒子滤波的微小卫星姿态确定算法［J］.中国惯性技术学报，2007，15（4）：426－430.Wu Hailiang，Wang Huinan，Chen Zhiming，et al.Particle filtering－based algorithm for micro－satellite altitude determination［J］.Journal of Chinese Inertial Technology，2007，15（4）：426－430.

［5］章飞，周杏鹏，陈小惠.基于粒子滤波的交互式多模型多机动目标跟踪［J］.数据采集与处理，2011，26（2）：181－187.Zhang Fei，Zhou Xingpeng，Chen Xiaohui.Interacting multiple model tracking algorithm of multiple maneuvering targets based on particle filter［J］.Journal of Data Acquisition ＆ Processing，2011，26（2）：181－187.

［6］程水英，张剑云.粒子滤波算法中的有限收敛界［J］.数据采集与处理，2008，23（4）：481－485.Cheng Shuiying，Zhang Jianyun.Limited convergence bound in particle filtering algorithms［J］.Journal of Data Acquisition ＆ Processing，2008，23（4）：481－485.

［7］聂建亮，杨元喜，吴富梅.一种基于改进粒子滤波的动态精密单点定位算法［J］.测绘学报，2010，39（4）：338－343.Nie Jianliang，Yang Yuanxi，Wu Fumei.An algorithm of dynamic precise point positioning based on modified particle filtering［J］.Acta Geodaetica et Cartographica Sinica，2010，39（4）：338－343.

［8］田世君，陈俊，皮亦鸣.粒子滤波在高动态GPS定位中的应用［J］.测绘学报，2007，36（3）：274－278.Tian Shijun，Chen Jun，Pi Yiming.Particle filtering and its application for kinematic GPS positioning with high speed movement［J］.Acta Geodaetica et Cartographica Sinica，2007，36（3）：274－278.

［9］Fredrik Gustafsson，Fredrik Gunnarsson.Particle filters for positioning，navigation，and tracking［J］.IEEE Trans on Signal Processing，2002，50（2）：425－437.

［10］Arulampalam M S，Maskell S，Gordon N，et al.Atutorial on particle filters for online nonlinear／non－Gaussian Bayesian tracking［J］.IEEE Transactions on Signal Processing，2002，50（2）：174－188.

［11］赵琳，聂琦，高伟.基于MCMC方法的正则粒子滤波算法及其应用［J］.仪器仪表学报，2008，29（10）：2156－2162.Zhao Lin，Nie Qi，Gao Wei.Regularized particle filtering algorithm and its application based on MCMC method［J］.Chinese Journal of Scientific Instrument，2008，29（10）：2156－2162.

［12］Kaplan E，Hegarty C.Understanding GPS：principles and applications［M］.2nd Edition.MA，US：Artech House，Inc，2006：239－264.