四元数数据投影DOA跟踪算法

陶 军 虞 飞 林智勇

（空军航空大学航空控制工程系，长春，130022）

引 言

电磁矢量传感器具有极化敏感特性，因而具有比传统的标量传感器更优越的性能。基于电磁矢量传感器阵列的数学模型目前有两种：一种是传统的复数域长矢量模型，它是将各个相互垂直的天线分量的输出数据按照阵列空间维数展开排列，从而形成一个长的数据矢量，故称之为长矢量数据模型。此模型的优点是可利用复数矩阵代数方法进行逐个分量处理，但由于该模型没有考虑矢量传感器内部各个天线分量的垂直关系，而是简单地将所有分量的输出数据排成一个列矢量，因此它破坏了各分量输出数据本身所具有的矢量结构［1］；另一种是四元数模型，它将每个阵元的各分量接收数据合成为一个四元数，突破了传统的基于复数域长矢量模型的局限性，利用四元数的正交特性很好地考虑了信号分量之间的垂直关系，从而对矢量传感器阵列进行了更全面的描述。在某些方面，四元数模型比基于复数域的长矢量模型更有利于矢量传感器阵列的信号处理。

近年来，基于四元数模型的矢量传感器阵列信号处理已经得到了长足的发展［1－5］。文献［1～3］已经成功地将多重信号分类法（Multiple signal classification，MUSIC）算法和旋转不变子空间算法（Estimating signal parameters via rotational invariance techniques，ESPRIT）算法引入到四元数框架下，得到了优于长矢量模型的估计性能，这些算法的一个共同特点是都用到了静态数据协方差矩阵的特征分解。由于实际应用中，目标（如飞机等）通常是移动的，需要对其波达方向（Direction of arrival，DOA）进行准确的跟踪估计。为了解决DOA跟踪问题，近年来，子空间跟踪算法［6－10］得到了广泛的研究。这些算法利用当前时刻接收数据对先前估计的子空间进行更新，具有较小的运算量。目前国内外对子空间跟踪类算法的研究主要是基于标量传感器阵列，而基于矢量传感器阵列的跟踪问题研究相对较少。文献［11］研究了利用叉乘（Cross product）算法对电磁波的跟踪问题，但该方法仅适用于单信号源情形。

针对上述问题，本文提出了一种基于四元数模型的数据投影（Quaternion data projection method，QDPM）跟踪算法，实现了利用矢量传感器阵列对多个信号的DOA进行跟踪。此算法对初始化条件引起的波动具有很强的鲁棒性，并且具有比常规DPM （Data projection method）算法更快的收敛速度，尤其在信号角度变化较剧烈时体现得更明显。此外，在低信噪比的情况下，QDPM算法比DPM算法具有更高的DOA跟踪精度。

1 阵列的四元数接收模型

假设均匀线性阵列（Uniform linear array，ULA）由L个沿y轴正方向排列的电磁矢量传感器组成，每个阵元采用沿x，y轴严格正交的电偶极子对，在空间同一点处放置，同时接收空间中x和y方向的电场分量，则此两分量简化矢量传感器的空间响应矢量为［4］

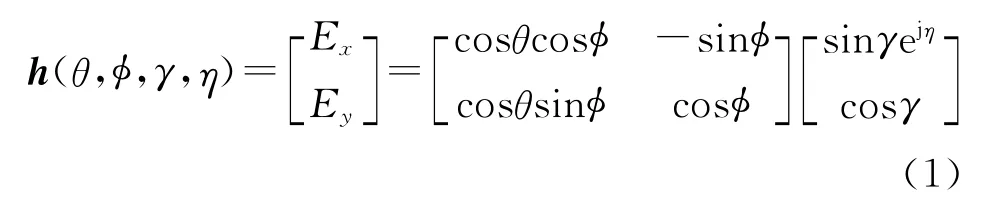
考虑一个窄带、远场电磁横向极化信号在各向同性、均匀介质中传播，则x和y轴方向上的电场强度分量分别为

式中s（t）是信号的复包络。将这两个方向上的电场分量合成为一个四元数，即

式中，p（θ，γ，η）是一个四元数，将四元数域记为“Q”。通过上述方式，将两个复数合成为一个四元数。下面，将上述单个两分量矢量传感器扩展到矢量传感器阵列情形。设上述均匀线阵以坐标原点上的阵元为参考阵元，则整个阵列的四元数空间响应表达式为

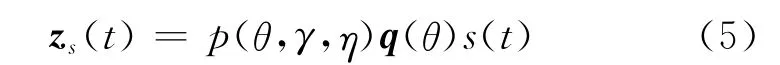
式中，q（θ）＝［q1（θ），…，qL（θ）］T为阵列的空域导向矢量，这里（·）T表示矩阵的转置。ql（θ）为第l个阵元的空间相移因子，且

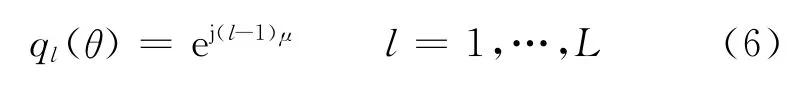
考虑K（K＜L）个远场、窄带完全极化电磁信号从不同方向入射到均匀线性阵列，同时考虑测量（接收）噪声的影响，则阵列输出矢量的四元数模型为

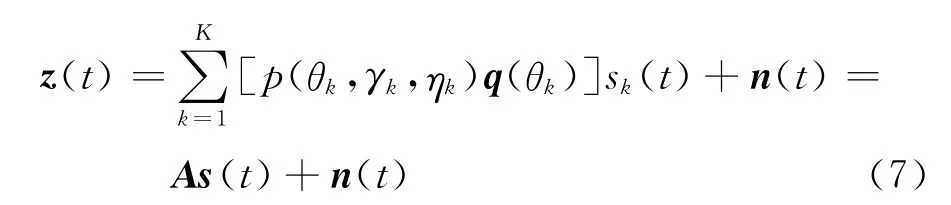
式中：A＝［p（θ1，γ1，η1）q（θ1），…，p（θK，γK，ηK）q（θK）］为阵列的L×K维四元数方向矩阵，且p（θk，γk，ηk）中包含了信号的角度和极化信息。s（t）＝［s1（t），…，sK（t）］T为信号的K×1维矢量，其中表示第k个信 号的复包络，pk表示第k个信号的功率，σk（t）是零均值单位方差的复随机过程，c表示波的传播速度，φk是第k个信号在［0，2π）之间均匀分布随机相位。n（t）＝［n1（t），…，nL（t）］T∈QL×1为阵列四元数加性噪声矢量，其中表示第l个矢量传感器的四元数加性噪声，而nlx（t）和nly（t）分别为x和y轴方向上的复数加性噪声分量。

2 基于四元数模型的数据投影跟踪算法

本文提出的QDPM跟踪算法是通过四元数矩阵的QR分解，来获得K个主特征向量，亦即信号子空间，使得在子空间更新过程中，各子空间向量之间的正交性得以保持，从而保证了DOA估计的精度。

引理［12］设Rt∈CL×L为一个对称非负定方阵，设λ1≥…≥λK＞λK＋1≥…≥λL≥0为其L个特征值，而u1，…，uL为其相应的特征向量。考虑L×K维矩阵序列｛Us（t）｝，定义迭代式

式中，orthnorm表示通过复数域QR分解或改进的Gram－Schmidt正交化等方法实现标准正交化。如果矩阵（0）［u1，…，uK］非奇异，则

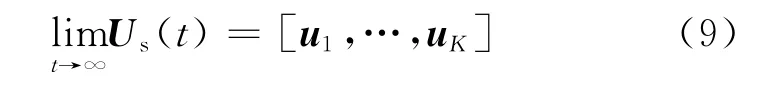
式中，（·）H表示复矩阵的共轭转置运算。文献［6］通过一种自适应处理实现了引理中的正交迭代过程

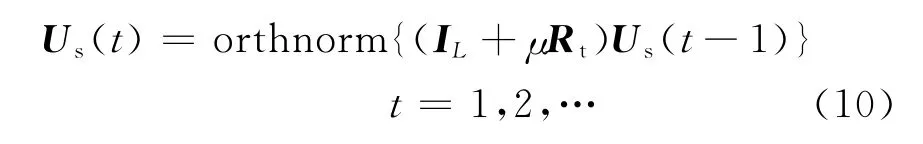
式中：μ是一个小标量参数，称为步长因子，IL表示L维的单位阵。在阵列信号处理中，引理中的非负定方阵Rt∈CL×L为阵列接收数据的协方差矩阵，Us（t）则为信号子空间在t时刻的更新值。对Rt的选择不同，得到的子空间跟踪算法也就不同了。本文的QDPM方法选择采用阵列在t时刻的瞬时接收数据的协方差矩阵来代替Rt，即Rt＝z（t）z◁（t），但应注意，此时Rt∈QL×L。

QDPM算法主要是通过L×L维的瞬时接收数据协方差矩阵Rt来实现对L×K维信号子空间的跟踪。在每一次迭代中，我们可以更新计算出当前时刻信号子空间的一组基向量，记为Us（t）。对Us（t）的更新计算包括数据压缩和压缩矩阵正交化两个步骤，即

这里，T（t）∈QL×K可以看作是一个L×1维数据矢量z（t）与一个K×1维的压缩数据矢量之间的互相关矩阵，而这个压缩数据矢量为

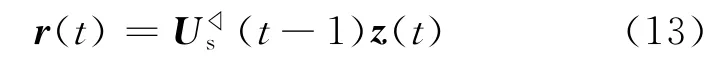
通过数据压缩过程，本文将T（t）∈QL×K和r（t）∈QK×1存入到数据存储空间，而不用像一般的子空间类算法一样需要存储数据协方差矩阵Rt∈QL×L和阵列接收数据z（t）∈QL×1，在DOA跟踪算法中，其节省的数据存储空间是很可观的。压缩矩阵的正交化的目的是确保在子空间的更新过程中，各子空间向量之间的正交性能够得到保持，以保证DOA跟踪估计的精度。综上分析可得到如下的QDPM算法：

对t＝1，2，…

（1）计算压缩数据矢量r（t）＝（t－1）z（t）；

（2）计算互相关矩阵T（t）＝（1－ρ）Us（t－1）＋ρz（t）r◁（t）；

（3）对互相关矩阵进行 QR分解，即T（t）⇒Q（t）R（t）；

（4）取正交矩阵Q（t）的前K列向量，构造的矩阵即为信号子空间Us（t）的更新值；

（5）通过四元数域的 ESPRIT 算法［3］估计出信号在t时刻的DOA；

算法初始化：根据引理可知，Us（0）只要是由K个线性无关的列向量构成的矩阵即可，只是收敛速度不同。一般可以设Us（0）＝［e1，…，eK］，式中ei表示单位矢量，除了第i个元素为1外，其余都为0。

需要注意的是，QDPM算法中的各种运算都是四元数值之间的运算，不同于DPM算法中的复数域运算，而在计算量方面，虽然四元数比复数的计算量大，但是，在QDPM算法中，四元数矩阵Us（t），z（t）和T（t）的行数都只是DPM 算法中对应矩阵分量行数的一半，因此，QDPM算法的计算复杂度与DPM算法一样，仍为O（L2K）。在第（2）步中小标量参数ρ满足0＜ρ＜1，称为遗忘因子，可以看出，遗忘因子ρ越大，前一时刻信号子空间的估计值对当前时刻信号子空间估计起到的作用越弱，反之作用越强。

3 仿真实验

考虑一个由5个排列在y轴上的二分量电磁矢量传感器构成的均匀线性矢量传感器阵列，相邻两个阵元的间距取为波长的一半，即：Δ＝λ／2。考虑两个等功率窄带独立、完全极化横向电磁（Transverse electromagmetic，TEM）平面波的信号源入射到上述阵列，且阵列对空间信号单次采样，加性噪声假设为零均值高斯白噪声，信噪比（Signal－to－noise ratio，SNR）定义为：SNR＝10lg（Ps／Pn），Ps和Pn分别为信号和噪声的平均功率。

3.1 遗忘因子ρ对QDPM跟踪性能的影响

假设两个信号相对于阵列初始DOA为：θ＝［30°40°］。信号源移动的角度变化律分别为：θ1＝30°－t×0.05°，θ2＝40°＋t×0.05°；两信号的极化参数（γ，η）分别为：（50°，30°），（30°，45°）；快拍数为300次；SNR＝15dB。图1（a，b，c）分别为遗忘因子取ρ＝0.01，ρ＝0.1，ρ＝0.5时 QDPM 算法对两个信号DOA跟踪曲线。

比较图1的3组仿真图可以看出，遗忘因子ρ越小，算法跟踪过程越稳定，且随着快拍数增大，跟踪曲线的波动越来越小，但此时跟踪受初始化条件的影响越大，导致算法的收敛速度下降。而随着遗忘因子的逐渐增大，算法，跟踪的稳定性有所下降，且跟踪估计值相对于实际DOA的偏差随着快拍数的增加并没有明显的收敛，波动较大，但此时算法的初始收敛速度加快了。这是因为，遗忘因子ρ越小前一时刻对信号子空间的跟踪结果在当前时刻迭代中的作用越大。

3.2 初始化条件对跟踪性能的影响

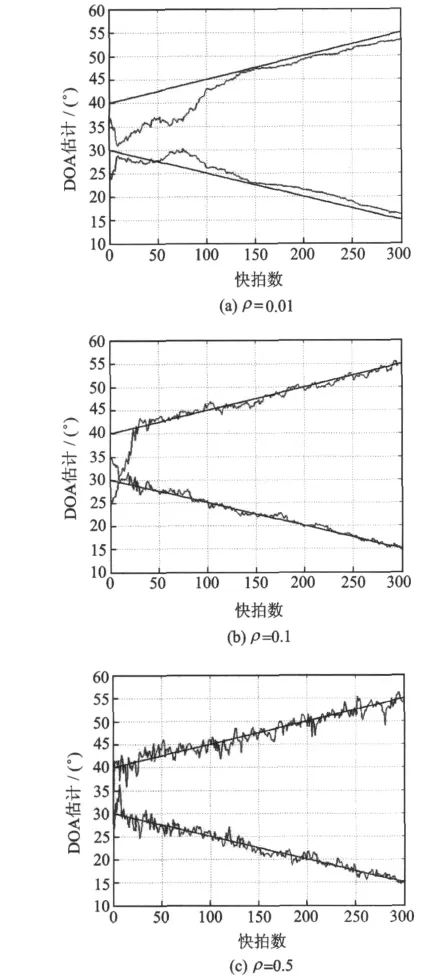
图1 QDPM对两个信号DOA的跟踪情况

假设两个信号源相对于阵列的初始DOA为：θ＝［30°40°］。信号源移动的角度变化律分别为：θ1＝30°－t×0.05°（平稳时变信号），θ2＝40°＋（周期变化信号）。两信号的极化参数（γ，η）分别为：（50°，30°），（30°，45°）。采样次数（快拍数）为50次。遗忘因子ρ＝0.1，信噪比取为SNR＝15dB。基于QDPM 算法、DPM 算法［13］和秩－1子空间跟踪（Rank－one subspace tracking，ROST）算法［14］分别进行仿真实验，图2中给出了DOA估计随快拍数的变化曲线。

从图2的仿真结果可以看出，在相同的初始化条件下，QDPM算法的波动最小，并且收敛总体最快（在第15次快拍时基本收敛），这说明QDPM算法对初始化条件引起的波动具有很强的鲁棒性，而DPM算法和ROST算法的初始波动范围很大，在收敛性方面，DPM算法在第25次快拍时才达到收敛，ROST算法虽然在平稳时变信号情况下的收敛很快，但是在角度变化较剧烈（如：周期时变信号）的情况下其收敛性明显不如前两种算法。

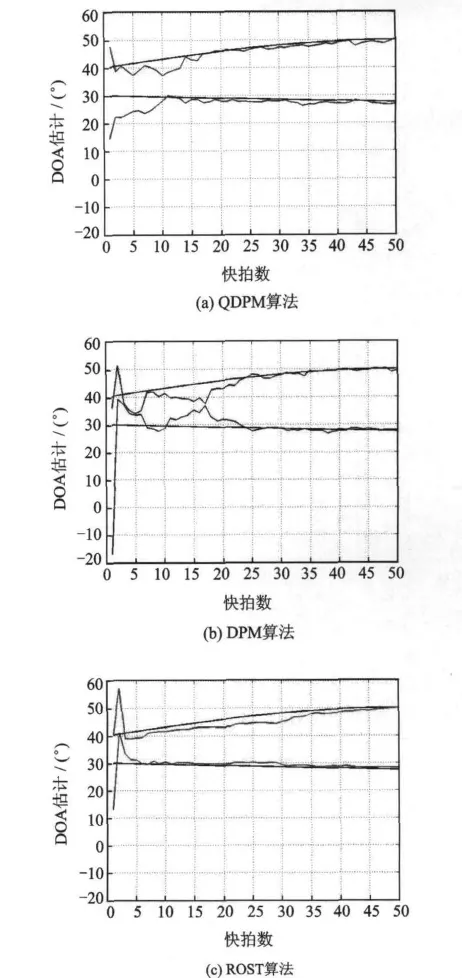
图2 3种跟踪算法的初始性能比较

3.3 DOA跟踪精度的比较

图3中给出了3种算法在跟踪区间内的DOA估计随快拍数的变化曲线，除了快拍数取300外，所有仿真条件同3.2节。由图3的3组仿真曲线可以看出，当信噪比与遗忘因子一定时，随着信号源方向的改变，3种算法都能实现对目标信号DOA的成功跟踪。在平稳时变信号的情况下，3种算法的跟踪精度相差不多。但是当角度变化较剧烈（如：周期时变信号）时，可以看出 QDPM算法对DOA的跟踪精度明显高于另外两种算法，DPM算法的弱点主要体现在当两个目标的DOA接近时，跟踪的误差较大，而ROST算法的跟踪曲线总体滞后于实际的DOA变化曲线，其跟踪误差显然最大。

图3 3种跟踪算法的跟踪精度比较

为了更直观地比较上述3种跟踪算法的跟踪精度，图4中给出了3种算法在跟踪区间内DOA估计的均方根误差（Root mean square error，RMSE）随SNR的变化曲线，除了SNR外，所有仿真条件同3.2节。这里取跟踪区间为t＝［25，300］，以消除初始化对跟踪的影响，从而更合理地评价3种算法的跟踪精度。

图4 DOA估计的RMSE随信噪比变化曲线

从图4的仿真结果可以看出，随着SNR的增加，这两种算法DOA估计的RMSE都是逐渐减小的，说明其跟踪性能越来越好。在同一SNR条件下，QDPM算法的RMSE曲线始终位于最下方，说明此时QDPM算法的跟踪精度高于DPM算法和ROST算法，尤其在低SNR情况下，这种优势更明显。

4 结束语

本文基于两分量简化矢量传感器阵列的四元数时域信号模型，提出了一种基于四元数模型的数据投影DOA跟踪算法，实现了利用矢量传感器阵列对多个信号的DOA进行跟踪。仿真结果表明：QDPM算法对初始化条件引起的波动具有较强的鲁棒性，在低SNR的情况下，QDPM算法对DOA的跟踪精度明显高于常规DPM算法。因而，QDPM算法非常适合于SNR很低以及对收敛速度要求较高的场合下对快变信号方向的跟踪。

［1］Miron S，Le Bihan N，Mars J.Quaternion－music for vector－sensor array processing［J］.IEEE Trans on Signal Processing，2006，54（4）：1218－1229.

［2］Le Bihan N，Miron S，Mars J.MUSIC algorithm for vector－sensors array using biquaternion［J］.IEEE Trans on Signal Processing，2007，55（9）：4523－4533.

［3］Gong Xiaofeng，Xu Yougen，Liu Zhiwen.Quaternion ESPRIT for direction finding with a polarization sensitive array［C］／／ICSP2008Proceedings.Beijing，China：Chinese Institute of Electronics，2008：378－381.

［4］崔伟，陶建武，徐惠斌.极化信号波达方向估计算法［J］.兵工学报，2010，31（7）：982－986.Cui Wei，Tao Jianwu，Xu Huibin.A new estimation algorithm of direction－of－arrival［J］.Acta Armamentarii，2010，31（7）：982－986.

［5］陶建武，常文秀.四元数最小均方误差算法及其在波束形成中的应用［J］.航空学报，2011，32（4）：729－738.Tao Jianwu，Chang Wenxiu.Quaternion MMSE algorithm and its application in beamforming［J］.Acto Aeronautica et Astronautica Sinica，2011，32（4）：729－738.

［6］Xenofon G D，George V M.Fast and stable subspace tracking ［J］.IEEE Trans on Signal Processing，2008，56（4）：1452－1465.

［7］Imran A，Doug N K，Taikyeong T J.A new subspace tracking algorithm using approximation of Gram－Schmidt procedure［C］／／International Conference on Information and Multimedia.Jeju Island，South Korea：IEEE Computer Society，2009：244－248.

［8］孟艳，汪晋宽，朱俊，等.基于子空间跟踪的空时多用户检测［J］.数据采集与处理，2008，23（6）：702－705.Meng Yan，Wang Jinkuan，Zhu Jun，et al.Spacetime multiuser detection based on subspace tracking［J］.Journal of Data Acquisition and Processing，2008，23（6）：702－705.

［9］Badeau R.Fast approximated power iteration subspace tracking［J］.IEEE Trans on Signal Processing，2005，53（8）：2931－2941.

［10］Toshihisa T.Fast generalized eigenvector tracking based on the power method［J］.IEEE Signal Processing Letters，2009，16（11）：969－972.

［11］Nehorai A，Tichavsky P.Cross－product algorithm for source tracking using an EM vector sensor［J］.IEEE Trans on Signal Processing，1999，47（10）：2863－2867.

［12］Golub G H，Van Loan C F.Matrix computation［M］.3rd Edition.Baltimore and London：The Johns Hopkins University Press，1996.

［13］Yang J F，Kaveh M.Adaptive eigen－subspace algorithm for direction or frequency estimation and tracking［J］.IEEE Trans Acoust Speech，Signal Process，1988，36（2）：241－251.

［14］陈辉，王永良.秩－1子空间跟踪算法［J］.电子与信息学报，2002，24（5）：626－630.Chen Hui，Wang Yongliang.A method of rank－1 subspace tracking［J］.Journal of Electronics and Information Technology，2002，24（5）：626－630.