基于平方根UKF双向滤波的单站无源定位算法

黄耀光 高 博 李建新 黄山奇

（1.解放军信息工程大学信息工程学院，郑州，450002；2.中国人民解放军65022部队，沈阳，110000）

引 言

随着现代电子战中隐身技术、反辐射导弹的广泛应用，有源定位系统面临严重的生存威胁。而无源定位技术因为隐蔽性强的特点，可以增强定位系统在电子战环境下的反侦察、反干扰、抗软硬杀伤力等能力。目前无源定位系统按照观测站的数目可以分为单站无源定位［1］和多站无源定位［2］，其中单站无源定位因具有设备简单、系统相对独立、机动性好等特点，成为当前无源定位领域的研究热点。

单站无源定位是一个典型的非线性滤波问题。其中如何提高滤波器的定位精度、稳定性和收敛速度一直是研究的重点。传统的非线性滤波算法主要包括扩展卡尔曼滤波（Extended Kalman filter，EKF）及其衍生算法，这些算法的核心是将非线性函数线性化，通过对非线性方程进行泰勒级数展开，并作一阶近似实现的。该类算法的缺点主要是非线性误差导致滤波器性能不稳定，容易发散。而无迹卡尔曼滤波（Unscented Kalman filter，UKF）通过选取一些确定性采样点来近似随机变量的概率分布，使计算精度至少能够达到二阶，避免了对非线性观测模型的线性化近似和雅克比矩阵的计算，性能优于 EKF及其衍生算法［3－8］。但是，在单站无源定位中，UKF算法由于数值计算舍入误差、可观测性弱（初始误差较大）和观测噪声大等因素的影响容易产生滤波性能不稳定、收敛速度慢和定位精度低等问题［9－10］。为解决以上问题，本文提出一种基于平方根UKF（Square－root UKF，SRUKF）双向滤波算法（Square－root unscented Rauch－Tung－Striebel smoother，SRURTS），新算法采用误差协方差阵的平方根形式代替协方差阵进行递推计算，保证了误差协方差阵的非负定性，从而提高该滤波算法的数值稳定性和运行效率；同时利用k时刻SRUKF滤波之后的状态估计值及协方差阵的平方根，对其采用URTSS后向平滑的方法，将得到的k－1时刻新的状态估计值及协方差阵的平方根作为初始值再对k时刻状态进行SRUKF滤波，并依次递推。新算法由于利用了k当前时刻测量量的信息，经反向预测得到的k－1时刻状态预测值一定比原来的状态预测值更接近k－1时刻状态的真实值，利用k－1时刻更精确的状态估计值作为初始条件滤波可以得到当前k时刻更精确的状态估计值。仿真结果表明，SRURTS算法较UKF算法和SRUKF算法，在算法的稳定性、收敛速度、定位精度，对初始值的鲁棒性方面都有所提高，是一种更加有效的单站无源定位算法。

1 单站无源定位模型

在三维直角坐标系下（见图1），k时刻观测站状态向量为目标辐射源状态向量为XA，k＝［xA，k，yA，k，

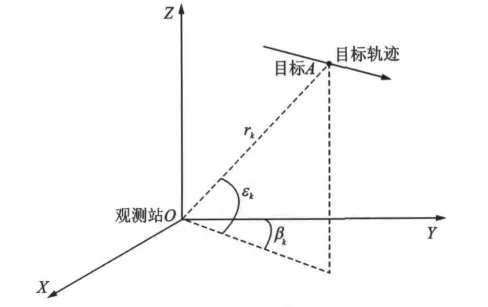
图1 观测站和目标在三维空间的几何关系图

1.1 系统状态方程

目标相对观测站作匀速运动，以观测站和目标辐射源相对运动状态向量Xk＝XA，k－XO，k＝［xk，为状态向量，则状态运动方程表示如下

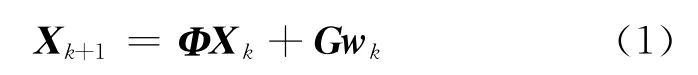
式中：xk，yk，zk为目标在坐标系中的位置分别为xk，yk，zk对时间t的导数，也就是速度变量，是状态转移矩阵，I3是3×3单位矩阵，03×3是3×3零矩阵，T是观测周期是状态噪声转移矩阵，wk是三维零均值高斯白噪声向量，协方差矩阵为Qw，那么状态噪声协方差矩阵为GQwGT。

1.2 系统测量方程

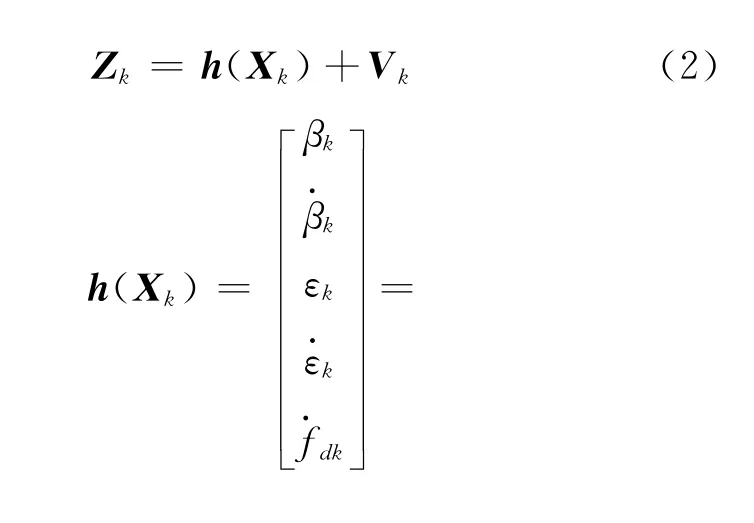
本研究以方位角βk及其变化率，俯仰角εk及其变化率，多普勒频率变化率作为观测量的单站无源定位方法为研究背景［11］，系统观测方程为式中：fT为目标辐射源频率，c为电磁波的传播速度为目标辐射源到观测站的径向距离，量测噪声Vk＝为零均值的高斯白噪声，其协方差矩阵为Rk。

2 基于SRUKF双向滤波递推算法

双向滤波递推算法是对当前k时刻状态进行SRUKF滤波，然后利用k时刻SRUKF滤波得到的状态估计值及协方差阵的平方根，对其采用URTSS后向平滑的方法，得到k－1时刻的新的状态估计值及协方差阵的平方根，将其作为初始值再对k时刻状态进行SRUKF滤波，并依次递推。

2.1 SRUKF滤波

SRUKF算法［12］只需要误差协方差阵的平方根，而不需要完整的协方差阵，因此，在计算中只需存储和运算平方根因数，这样可以降低计算负担，提高计算效率；另外，利用平方根得到的协方差阵一定是非负定的，避免了UKF算法由于误差协方差非正定而引起的滤波发散，提高了滤波稳定性。SRUKF算法流程如下：

（1）系统初始化

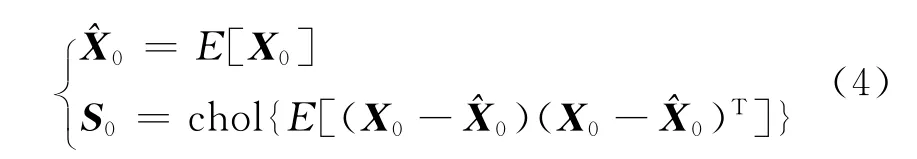
式中chol表示Cholesky分解。

（2）选取Sigma点及加权系数

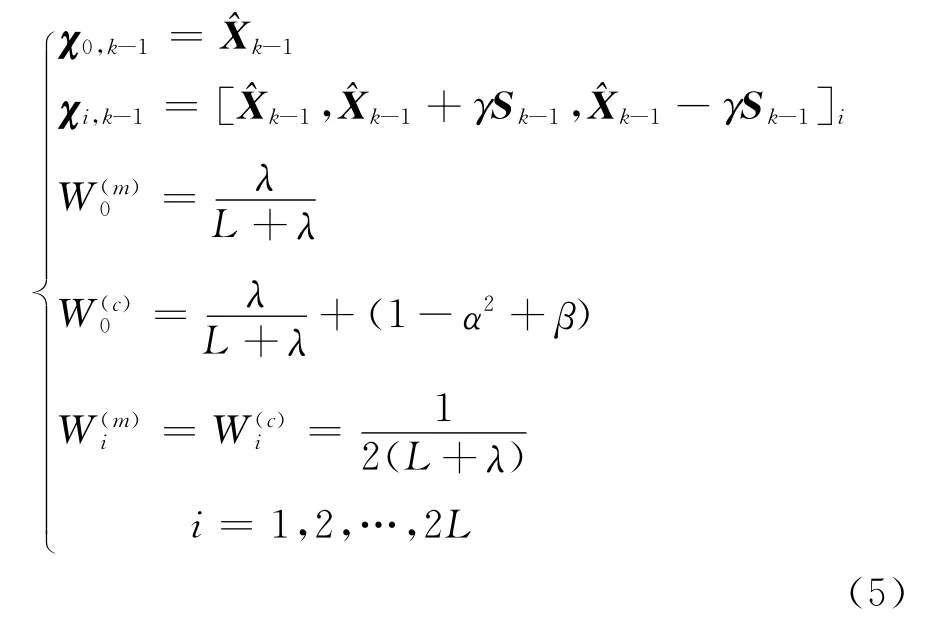
（3）时间更新

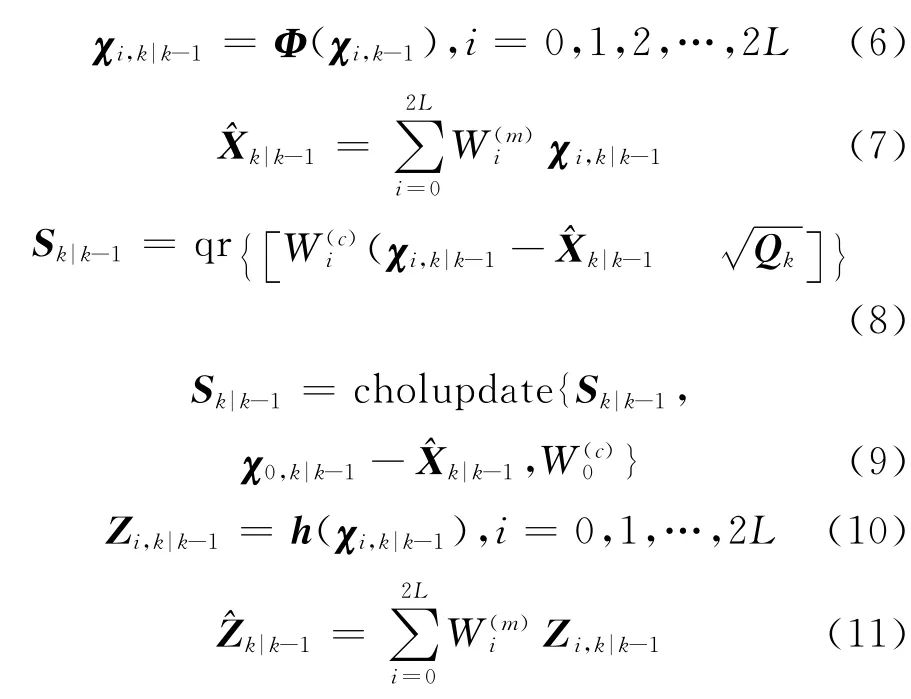
式中qr和cholupdate分别表示QR分解和Cholesky一阶更新，为标准的Matlab指令。

（4）量测更新

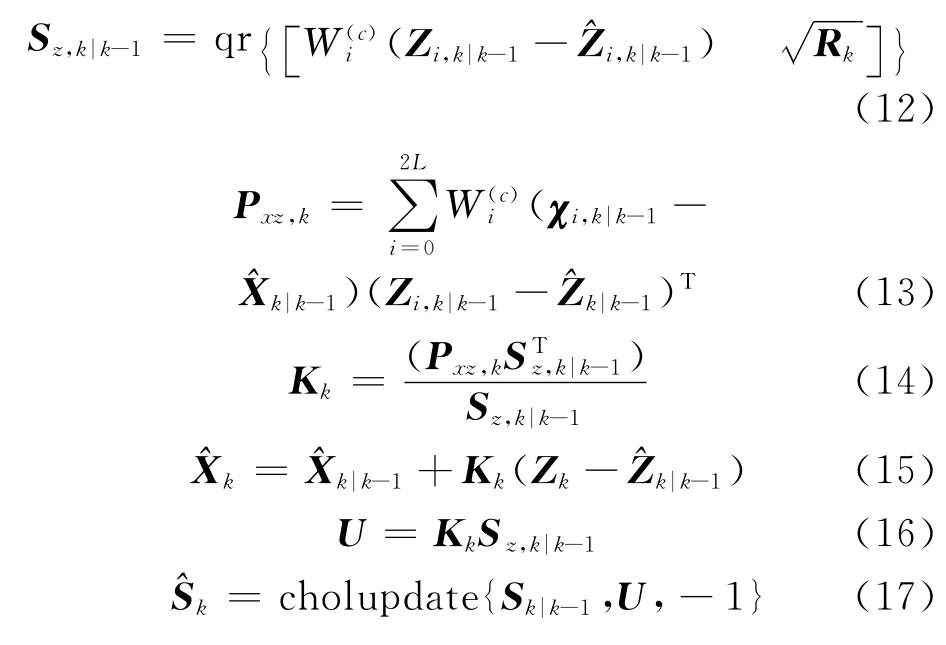
2.2 URTSS后向平滑方法

文献［13～14］给出了URTSS后向平滑算法如下

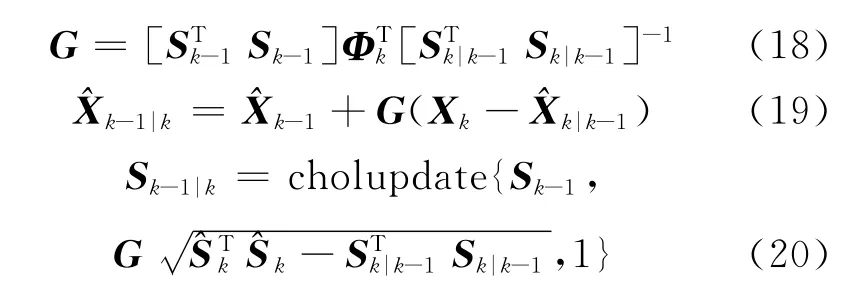
2.3 第二次SRUKF正向滤波

SRUKF双向滤波递推算法示意图如图2所示，图中① ② ③ 表示算法运算顺序，该算法的实现步骤总结归纳为：

（1）当k≥1时，按式（4～17）得到k时刻的状态估计值；

（2）根据式（18～20）进行 URTSS后向平滑，得到k－1时刻的状态预测值；

（3）将作为k－1时刻新的状态预测值，再按式（4～17）进行更新，得到状态估计值

按照以上步骤进行递推，就可以依次得到各个时刻的状态估计值。当k≥1时，每一个时刻的状态估计值有3个，两个是以前一时刻估计值为初始条件进行正向滤波得到的，另一个是以后一时刻估计值后向平滑滤波得到的，在这里把作为最终当前时刻的状态估计值。

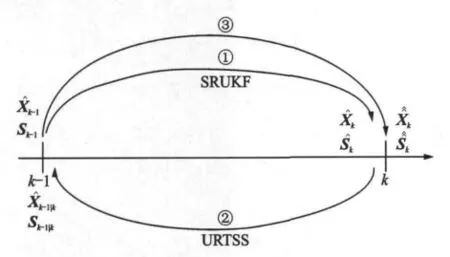
图2 算法示意图

3 算法仿真与结果分析

采用相对距离误差（Relative range error，RRE）来描述算法的收敛性能，其定义为

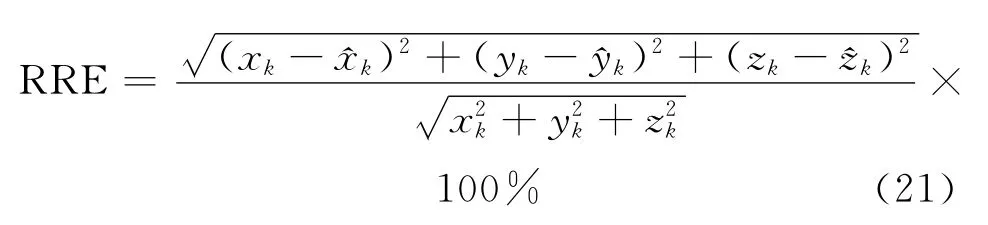
式中：（xk，yk，zk）为k时刻的真实位置（），为k时刻位置的估计值。

假设目标辐射源作带加速度扰动的匀速直线运动，目标真实的初始位置为x0＝180km，y0＝90km，z0＝8km，速度 为＝ －300m／s，＝100m／s＝0m／s，加速度扰动wk的协方差矩阵为diag［（0.1m／s2）2，（0.1m／s2）2，（0.1m／s2）2］。观测站位于坐标原点，辐射源信号载频为10GHz，观测周期T＝0.1s，观测时间持续100s。

为了检验本文算法（SRURTS算法）滤波的稳定性、收敛速度和定位精度，将其与UKF算法、SRUKF算法进行比较，在初始状态估计相对误差20%的条件下，给定3组不同的观测精度，参数的观测精度分别为：

（1）σβ＝2mrad，σ˙β＝0.15mrad／s，σε＝0.1mrad，σ˙ε＝0.1mrad／s，σ˙fd＝0.5Hz／s；

（2）σβ＝4mrad，σ˙β＝0.3mrad／s，σε＝0.3mrad，σ˙ε＝0.2mrad／s，σ˙fd＝1Hz／s；

（3）σβ＝10mrad，σ˙β＝0.5mrad／s，σε＝0.5mrad，σ˙ε＝0.9mrad／s，σ˙fd＝4Hz／s；

在不同的测量精度下作100次 Monte－Carlo实验，在定位跟踪结束时刻RRE＜15%则视本次实验收敛，否则视为发散。定位精度为跟踪结束时RRE的统计平均值，仿真结果如表1和图3所示（剔除发散的实验结果）。

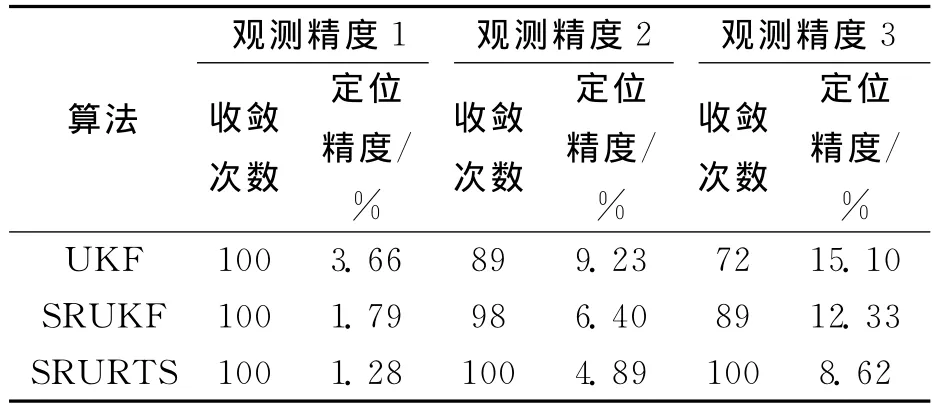
表1 初始状态估计相对误差为20%时不同观测精度稳定性与定位精度比较

由表1可以得知，在高精度观测时，算法的性能均有较好的表现，但随着观测精度逐渐降低，各算法的性能开始发生变化。各算法的定位精度随着观测精度的降低而降低，相比较SRURTS算法定位精度最高，SRUKF算法次之，UKF算法最差；同时随着观测精度逐渐降低，UKF算法和SRUKF算法发散次数开始增多，尤其UKF算法发散次数增加最多，即滤波稳定性最差，而SRURTS算法稳定性不受影响。

从图3可以很直观地得知，随着观测精度的逐渐降低，各算法的收敛速度变慢，其中UKF算法收敛速度影响最大；在不同的观测精度下，SRURTS算法的收敛速度最快，SRUKF算法次之，UKF算法收敛速度最慢。

此外，为了检验SRURTS算法对初始值的鲁棒性，在中等观测精度2的条件下，初始状态估计相对误差取从0到100%的11组值。在不同的初始状态估计相对误差下，作100次Monte－Carlo实验，定位精度为跟踪结束时RRE的统计平均值，仿真结果如表2和图4所示。

图3 初始状态估计相对误差为20%时不同观测精度各算法的统计平均曲线

表2 观测精度2时不同初始状态估计误差下各算法的定位精度 %

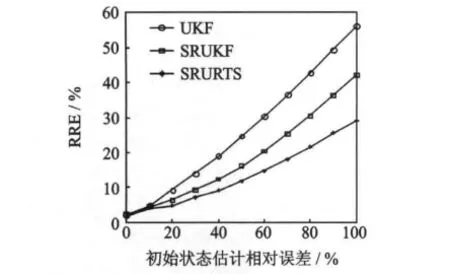
图4 观测精度2时不同初始状态估计误差下各算法的定位精度曲线

由表2看出，在初始状态估计无误差时，各算法的定位精度都较高，其中SRURTS算法的定位精度略高于UKF算法和SRUKF算法。随着初始状态估计误差的增大，各算法的定位精度逐渐降低。不论初始状态估计误差多大，UKF算法定位精度都是最低的，SRUKF算法次之，SRURTS算法的定位精度是最高的，而且即使初始状态估计相对误差为20%时，定位精度仍能在5%以内。

由图4可以看到，各算法随着初始状态估计相对误差增大时定位精度的变化趋势，各算法的定位精度均随着初始状态估计误差的增大而降低，其中UKF算法的变化趋势最快，也说明UKF算法对初始值是最敏感的，SRUKF算法次之，而SRURTS算法的变化趋势最慢，表明了该算法对初始值的鲁棒性最好。

归纳以上的分析可以得到，SRURTS算法在滤波的稳定性、收敛速度、定位精度及对初始值的鲁棒性上均优于SRUKF算法和UKF算法。

需要指出的是SRURTS算法的计算量有所增加，与SRUKF算法相比，由于增加了后向平滑和又一次SRUKF滤波的过程，计算量是SRUKF算法的2倍多。

在内存为2GB，CPU主频为2.9GHz的计算机上用Matlab软件运行各算法，得到各算法单次递推平均所需时间见表3。

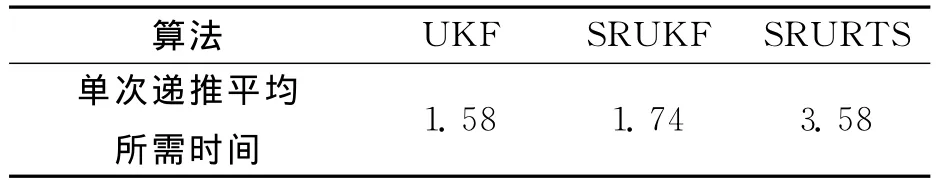
表3 不同算法实现时间比较 ms

由表3可知，尽管SRURTS算法增加了计算量，还是可以满足定位的实时性要求。

4 结束语

本文提出了一种基于平方根UKF双向滤波的单站无源定位算法（SRURTS算法），该算法在满足实时性要求的条件下，通过采用误差协方差阵的平方根形式进行递推计算和后向平滑的方法对UKF算法进行改进，适当增加了计算量，能够有效提高滤波的稳定性、收敛速度、定位精度及对初始值的鲁棒性。仿真结果也表明了SRURTS算法相对于UKF算法和SRUKF算法在初始状态估计误差大和低观测精度背景的条件下具有更好的定位跟踪精度和稳定性。该算法对单站无源定位系统工程化有较大的参考价值，同时也可以应用于其他无源定位和非线性滤波领域中。

［1］孙仲康，郭福成，冯道旺.单站无源定位跟踪技术［M］.北京：国防工业出版社，2008：98－100.Sun Zhongkang，Guo Fucheng，Feng Daowang.Single observer passive location［M］.Beijing：National Defense Industry Press，2008：98－100.

［2］何友，王本才.多站虚拟量测变换均值无源定位算法［J］.数据采集与处理，2012，27（1）：13－19.He You，Wang Bencai.Multi－sensor ME passive localization algorithm based on virtual measurement transform［J］.Journal of Data Acquisition and Processing，2012，27（1）：13－19.

［3］Julier S J，Uhlman J K.Unscented filtering and nonlinear estimation［J］.Proc of the IEEE，2004，92（3）：401－422.

［4］徐璟，何明浩，郁春来，等.固定单站被动目标跟踪算法性能分析［J］.电子信息对抗技术，2011，26（1）：29－33.Xu Jing，He Minghao，Yu Chunlai，et al.Analysis of single non－moving observer passive tracking algorithms［J］.Electronic Warfare Technology，2011，26（1）：29－33.

［5］宋骊平，姬红兵.多被动传感器UKF与EKF算法的应用与比较［J］.系统工程与电子技术，2009，31（5）：1083－1086.Song Liping，Ji Hongbing.Application and comparison of UKF and EKF algorithm in target tracking with multiple passive sensors［J］.Systems Engineering and Electronics，2009，31（5）：1083－1086.

［6］程水英.UKF与EKF在空对海单站TO－TMA中的应用［J］.数据采集与处理，2009，24（S1）：49－53.Chen Shuiying.Application of air－to－sea time－of－arrival only TMA based on UKF and EKF algorithm［J］.Journal of Data Acquisition and Processing，2009，24（S1）：49－53.

［7］Crassidis J L，Junkins J L.Optimal estimation of dynamic systems［M］.Boca Raton：CRC，2004：343－350.

［8］顾晓东，袁志勇，周浩.基于IMM－UKF的纯方位机动目标跟踪算法［J］.数据采集与处理，2009，24（S1）：88－91.Gu Xiaodong，Yuan Zhiyong，Zhou Hao.Bearingsonly tracking of maneuvering target based on IMMUKF algorithm［J］.Journal of Data Acquisition and Processing，2009，24（S1）：88－91.

［9］袁罡，陈鲸.基于UKF的单站无源定位与跟踪算法［J］.电子与信息学报，2008，30（9）：2120－2123.Yuan Gang，Chen Jing.An algorithm based on UKF for single observer passive location and tracking［J］.Journal of Electronics Information Technology，2008，30（9）：2120－2123.

［10］郁春来.利用空频域信息的单站无源定位与跟踪关键技术研究［D］.长沙：国防科学技术大学，2008.Yu Chunlai.Research on crucial technologies for single observer passive location and tracking via spatialfrequency domain information［D］.Changsha：National University of Defense Technology，2008.

［11］牛新亮，赵国庆，刘原华，等.基于多普勒变化率的机载无源定位研究［J］.系统仿真学报，2009，21（11）：3370－3373.Niu Xinliang，Zhao Guoqing，Liu Yuanhua，et al.Research on airborne passive location using Doppler changing rate［J］.Journal of System Simulation，2009，21（11）：3370－3373.

［12］Van Der Merwe R，Wan E A.The square－root unscented Kalman filter for state and parameter estimation［C］∥Proceedings of IEEE International Conference on Acoustics，Speech and Signal.New York：IEEE，2001：3461－3464.

［13］Liu H，Nassar S，El－Sheimy N.Two－filter smoothing for accurate INS／GPS land－vehicle navigation in urban centers［J］.IEEE Transaction on Vehicular Technology，2010，59（9）：4256－4267.

［14］S¨arkk¨a S.Unscented Rauch－Tung－Striebel smoother［J］.IEEE Transaction on Automatic Control，2008，53（3）：845－849.