基于修正STAP的高速空中机动目标检测方法

贾琼琼 吴仁彪 李 海

（中国民航大学天津市智能信号与图像处理重点实验室，天津，300300）

引 言

机载预警雷达，是预警机主要的传感器和情报来源。在信息技术日益发展的现代战争中，预警雷达发挥着重要作用。本文以相控阵机载预警雷达为背景，主要研究高速空中机动（本文仅考虑存在径向加速度的情况）目标检测问题。检测这类目标面临的主要难题有：（1）机载预警雷达下视工作时微弱目标信号往往淹没于因平台运动使多普勒谱展宽了的强地杂波中，仅用单个通道接收下来的回波信号（时域采样信号）进行多普勒处理的方法不能抑制与动目标相同多普勒频率的地物杂波［1－10］。（2）目标的高速运动会引起严重的距离走动，这会导致目标积累效果下降［11］。（3）目标的径向加速度引起的二次相位项会对回波信号产生时变调制（即产生多普勒走动），此时如果仍采用传统的相参积累方法处理线性调频信号（Linear frequency modulated，LFM）必然也会导致积累效果严重下降。

相位中心偏置天线（Displaced phase center antenna，DPCA）技术是同时利用多个通道接收的空时采样信号进行处理的方法，然而它容易受通道误差等各种非理想因素影响［1－4］。Brennan等人［5］提出了用空时二维采样信号进行自适应处理的方法（即STAP技术），其核心思想是利用杂波的空时耦合特性自适应地调节二维滤波器的响应滤除杂波，并保证对目标有足够的增益，它在一定程度上补偿了误差所造成的影响，大大改善了杂波抑制效果［1－10］。

但是，传统的STAP方法都是假设在相干处理时间（Coherent processing interval，CPI）内目标处于固定的距离单元（即不发生距离走动）。因此，必须设法对目标距离走动进行校正以提高动目标检测性能。Keystone变换可以在目标运动速度未知的情况下统一校正多个目标（包括地杂波）的线性距离走动，被广泛应用于雷达地面动目标成像［12－18］以及微弱目标检测领域［11，19］。

文献［20～22］在杂波不存在距离走动的前提下将Keystone变换与STAP相结合来实现高速微弱空中动目标的检测，并获得了良好的检测性能。但是，它仅仅针对的是匀速运动的高速目标，当目标作机动飞行时，径向加速度引起的二次相位项会对回波信号产生时变调制，此时文献［20～24］方法的检测性能将大大下降。针对目标存在多普勒走动时的目标检测，文献［23］提出了一种有效的方法，采用修正的导向矢量对多普勒走动项进行补偿，能够在目标存在多普勒走动的情况下，获得满意的动目标检测结果。但是该方法只针对目标低速运动（即不发生距离走动的情况下适用）。为了实现这类目标的有效检测，本文提出了一种用于机载相控阵预警雷达实现高速空中机动目标检测的新方法，其主要思想是先对回波数据进行杂波抑制，再利用Keystone变换校正目标距离走动，然后利用修正匹配滤波估计出目标加速度，接着根据所估计出的加速度对多普勒走动项进行补偿，最后进行常规空时二维波束形成实现目标能量积累。该方法不但避免了直接利用Keystone变换校正存在多普勒模糊的高速目标距离走动时影响杂波分布特性，进而降低STAP性能的问题［22］，而且补偿了由于目标加速度所造成的多普勒走动项，从而实现目标能量的有效积累。通过仿真实验验证了该方法的有效性。

1 问题描述

1.1 理想情况下的数据模型

考虑机载平台上沿航向方向放置的N元均匀线阵（Uniform linear array，ULA），阵元间距为d＝0.5λ，λ为工作波长，一个相干处理时间内发射K个脉冲，xnk为第n个阵元在第k个脉冲上对应的复采样值，则每一距离门上的接收数据可以写做一个如下的N×K矩阵［1］

假设在每个脉冲重复间隔内沿距离向的采样点数为L，则一个CPI的接收数据形成了一个N×K×L的三维数据块。将式（1）中的数据矩阵X按列排成一个NK×1的列向量，可记为x＝vec（X），就形成了一个空时快拍数据。假定单个距离门内最多存在一个目标，待检测单元的空时快拍（即一次数据）可写成

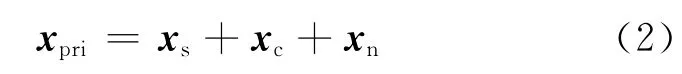
式中xs，xc和xn分别表示目标、杂波和噪声成分。xs可表示为

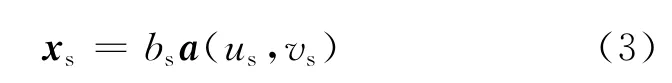
式中bs为目标回波复幅度，a（us，vs）为目标空时导向矢量，其归一化空间频率和时间频率分别为us＝2πdcosψs／λ和vs＝2πfd／fr，ψs表示目标来向角。其中空时导向矢量a（us，vs）有如下形式

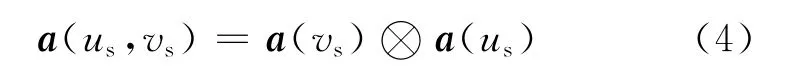
式中⊗表示Kronecker积，时域导向矢量a（vs）＝为K×1维列向量，空域 导 向 矢 量为N×1维列向量，（·）T表示转置运算。

1.2 机动目标数据模型

空中目标的高速运动会导致其回波处于不同的距离分辨单元，即产生了距离走动；并且，目标机动飞行时，还会导致多普勒走动。此时，将包含目标回波的一次数据记为

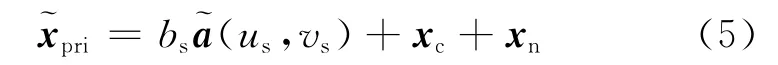
假设杂波无距离走动（载机运动速度不是很高时这一假设是合理的［21］），此时，杂波数据与目标不存在距离走动时相同，即式（5）xc和xn的分布特性与式（2）保持不变，而（us，vs）是存在距离走动和多普勒走动的目标导向矢量，有如下形式

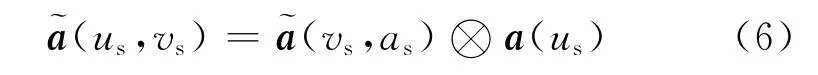
式中空域导向矢量a（us）保持不变，为了得到（vs），现考虑机动目标的时域回波模型，假设运动点目标的基带回波信号为

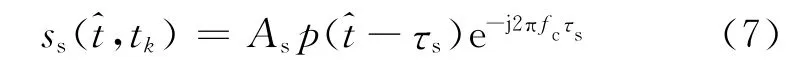
式中tk＝kT（k＝0，…，K－1）为慢时间，T为雷达发射脉冲重复周期。t＝t－tk为快时间，p（·）为回波包络，fc为载波频率，As为点目标回波的幅度，τs＝2Rs（tk）／c为回波时延，Rs（tk）为目标与雷达之间的瞬时距离。假设目标在CPI内做匀加速直线运动，则

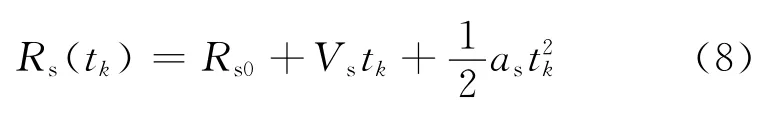
式中：Rs0为0时刻目标与雷达之间的距离，Vs为目标运动速度，as为目标运动的加速度。将式（8）代入式（7）可得

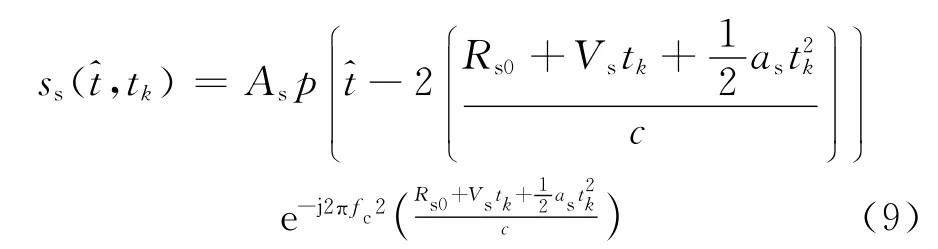
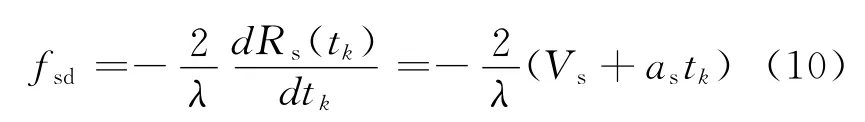
由以上分析可知

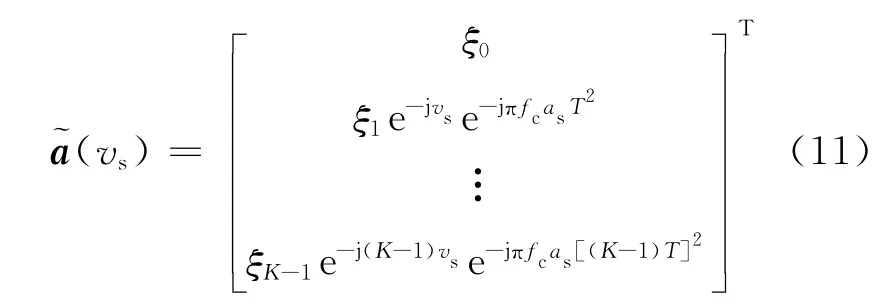
可以看出，当目标作匀加速直线运动时，目标时域导向矢量会发生变化，不利于目标能量积累。

2 高速空中机动目标检测新方法

高速目标存在严重的速度模糊，此时直接对回波数据进行Keystone变换的方法在校正目标距离走动的同时会对杂波特性产生影响进而降低后续STAP处理性能［21］，因此本节提出了一种新方法，该方法首先对回波数据进行杂波抑制，然后利用Keystone变换校正目标距离走动，从而避免了上述问题。并且对距离走动校正之后的数据进行修正匹配滤波估计出目标的加速度，然后根据估计值对由加速度所引起的多普勒走动项进行补偿，最后进行目标积累检测。下面介绍其原理。

2.1 杂波抑制原理

对干扰协方差矩阵R进行特征分解

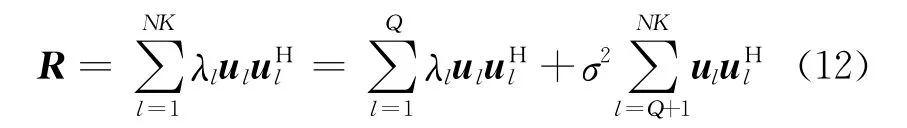
式中：λl（l＝1，2，…，Q）代表杂波特征值，σ2代表其余的NK－Q个噪声特征值，（·）H表示共轭转置运算。与杂波特征值对应的特征向量ul（l＝1，2，…，Q）张成杂波子空间Uc＝span｛u1，…，uQ｝，杂波子空间的正交补空间的投影矩阵为［1］

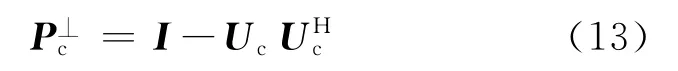
2.2 距离走动校正原理

对杂波抑制后的数据进行Keystone变换校正目标距离走动，首先将式（9）从快时间域变换到距离频率域，得

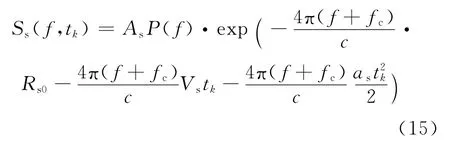
式中P（f）为p的傅里叶变换。式（15）的指数相位中第1项为常数项，它不影响后面的处理，第2项为距离走动项和多普勒偏移项，第3项为距离弯曲项和多普勒走动项。当第3项中的距离弯曲项可以忽略时，式（15）可以写成

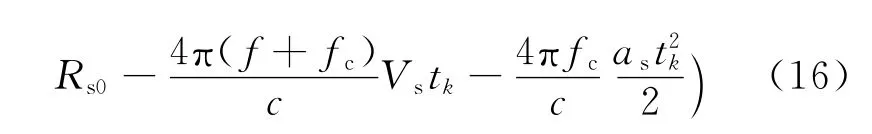
对于存在多普勒模糊的高速目标，Keystone变换与多普勒频率的模糊程度有关，目标的多普勒频率用fd表示，则fd与模糊后的多普勒频率fd0有如下关系

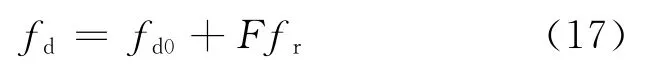
式中F为模糊数。定义一个虚拟时间ηk，令（fc＋f）tk＝fcηk，目标存在多普勒模糊情况下的 Keystone变换公式如下

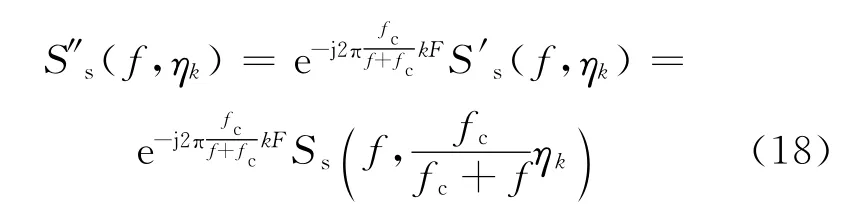
从式（18）可以看出，当动目标多普勒模糊数F取不同值时，意味着Keystone变换有不同的修正项将式（18）变换回快时间域可得

从式（19）可以看出，对于不同发射脉冲，目标回波信号峰值的位置始终是2Rs0／c，它只与初始时刻目标的位置有关，也就是说Keystone变换把原本位于不同距离单元的回波校正到同一距离单元，补偿了距离走动，此时式（20）中目标信号变成线性调制频率（Linear modulated frequency，LMF）信号。此时将一次数据记为xKproj，其中上标K表示经过Keystone变换。

2.3 多普勒走动项补偿原理

文献［19～20］中，目标距离走动校正后，直接进行常规空时二维波束形成能够有效地实现目标能量积累。但是，当目标机动飞行时，加速度引起的多普勒走动项使得上述方法不再适用。为此，本文采用修正的匹配滤波（即在常规匹配滤波器导向矢量中加入加速度项）对机动目标进行匹配检测，从而可以获得目标加速度估值。根据所获得的加速度值便可以补偿目标的多普勒走动。

修正匹配滤波器的权矢量定义为

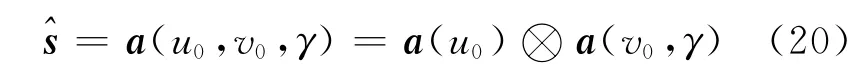
式中a（v0，γ）为修正的时域导向矢量

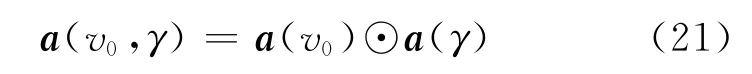
式中：a（v0）为初速度对应的时域导向矢量部分，a（γ）为加速度对应的时域导向矢量部分

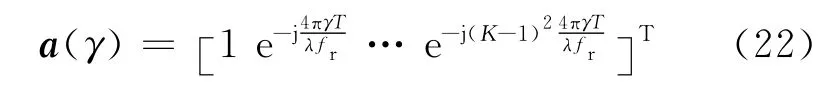
则修正的匹配滤波器输出为

图1为本文所提新方法流程图，具体步骤可归纳如下：

（1）利用估计得到的干扰空时二维协方差矩阵R的逆矩阵R－1来对雷达接收到的总回波数据进行杂波抑制；

（2）对抑制杂波后的数据进行Keystone变换校正目标距离走动；

（3）对步骤（2）的结果进行修正匹配滤波处理估计目标加速度，并根据所估计的加速度值补偿目标的多普勒走动项；

（4）对经上述处理后的空时二维数据乘以（a（us，vs））H，即进行常规空时二维波束形成，实现目标能量积累。

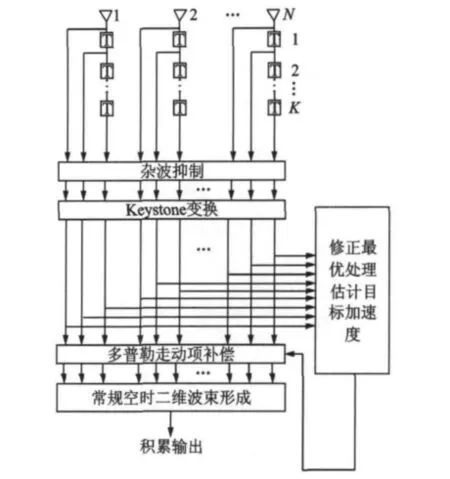
图1 本文方法实现框图

3 仿真实验

本节将通过仿真实验验证本文所提方法的有效性。仿真参数设置：天线阵为阵元数N＝16的正侧视理想均匀线阵，阵元间距d＝0.5λ，发射波长λ＝0.23m，相干处理脉冲数K＝64，载机速度Vp＝140m／s，输入信噪比（Signal－to－noise ratio，SNR）为－10dB，杂噪比（Clutter－to－noise ratio，CNR）为60dB，载机高度H＝8 000m，发射脉冲重复频率fr＝2 434.8Hz，雷达距离分辨率为ΔR＝10m，目标运动加速度为as＝1 000m／s2。根据上述参数计算可知，在相干处理时间内杂波的最大走动量为Rmax＝3.6m＜ΔR／2，可以忽略掉杂波走动的影响。

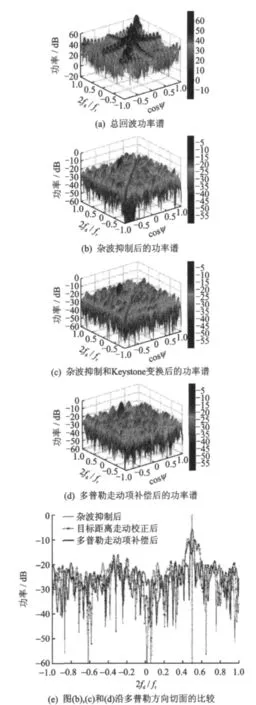
图2 Vs＝910m／s时回波数据的功率谱

图2给出了目标速度为910m／s，对应的多普勒模糊数为3时不同情况下回波数据的功率谱。图2中x横轴表示模糊后的归一化多普勒频率，y轴为空域锥角余弦，z轴表示功率值。图2（a）为总回波功率谱；图2（b）为经过本文所述方法抑制杂波后的功率谱；图2（c）为经过Keystone变换校正目标距离走动后的功率谱；图2（d）为经过本文所述多普勒走动项补偿后的功率谱。从图2（b）可以看出，尽管杂波被抑制，但是距离走动和多普勒走动项会导致目标主瓣展宽，目标能量非常微弱；经过Keystone变换校正目标距离走动后，目标回波被校正到同一距离单元，但是由于多普勒走动项的影响，目标仍未得到有效积累，如图2（c）；经过对由加速度引起的多普勒走动项进行补偿后能量得到了有效的积累，多普勒分辨率显著提高，如图2（d）。图2（e）沿多普勒方向分别取图2（b），2（c），2（d）的一个切面作对比，可以更加明显地看出，经过目标距离走动校正后，目标能量并未提高，但是目标信号形式发生了变化，变成一个线性调频信号的形式；经过多普勒走动项补偿后，目标能量显著增加，多普勒分辨率也大大提高。

图3比较了不同处理方法目标能量积累效果。其中两个目标速度分别为854m／s和910m／s，对应的多普勒频率（有模糊的归一化多普勒频率）分别为0.1和0.5。“直接最优处理”是直接经最优处理器处理的目标能量积累效果；“KF＋OAP”指先进行Keystone变换校正目标距离走动，再进行杂波抑制，最后利用修正最优处理器估计目标加速度并对其进行补偿；“新方法”是经本文所提方法处理后的目标能量积累效果。可以看出“直接最优处理”不能积累任何一个目标，这正是目标距离走动所导致的结果；“KF＋OAP”可以有效积累目标2，但不能积累目标1，这是由于目标存在多普勒模糊时，Keystone变换校正目标距离走动的同时导致杂波脊展宽和杂波抑制性能下降，且目标1处于展宽后的杂波脊上，因此不能被检测到；然而“本文方法”对两个目标均能够有效积累。

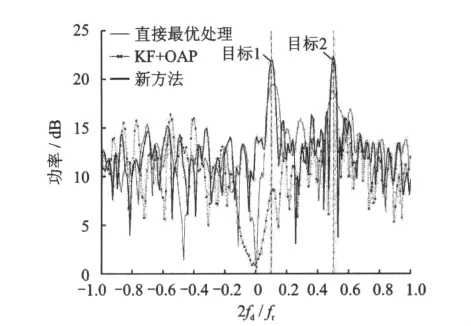
图3 目标能量积累效果比较

图4比较了不同处理方法的检测性能，图中横轴表示目标速度，纵轴表示改善因子。图4只给出了目标速度取正值的结果，当目标速度取负值时的结果与正值部分关于Vs＝0对称。“理想情况”指目标无距离走动的理想情况下STAP最优处理器处理的结果，它可以作为最佳性能的上界；其余各曲线所代表的含义同图3。可以看出，在目标存在距离走动和多普勒走动的情况下，若不考虑这些因素的影响将会导致严重的性能损失，如“直接最优处理”；由于目标存在多普勒模糊时，杂波和目标模糊数不同，此时直接利用Keystone变换校正目标距离走动会导致杂波脊展宽，这会降低主瓣杂波附近目标检测性能，并且随着目标多普勒模糊数的增大，Keystone变换导致杂波脊展宽更明显，因此“KF＋OAP”在主瓣杂波附近出现严重的性能损失的区域也逐渐扩大；而本文方法在整个区间内都能获得较好的性能。

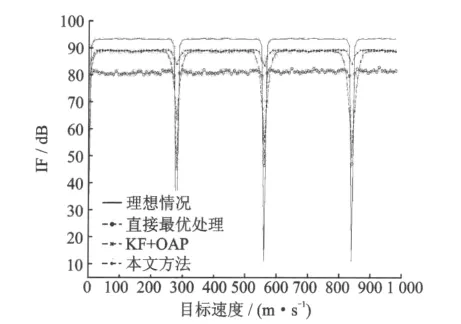
图4 不同处理方法改善因子比较

4 结束语

本文提出了一种先进行杂波抑制，再进行Keystone变换校正目标距离走动的新方法，从而避免了目标存在多普勒模糊时Keystone变换影响杂波分布特性，进而降低STAP性能的问题；然后利用修正匹配滤波器估计出目标的加速度，并根据所估计的值补偿目标加速度所引起的多普勒走动项；最后进行常规空时二维波束形成实现目标积累。仿真实验证明，当杂波不存在距离走动时，该方法较之传统方法性能显著提高。另外需要说明的是，本文方法只针对载机运动速度较低以及单目标（或模糊数相同的多个目标）的情况有效，当载机运动速度较高时会导致杂波也产生距离走动，这就需要进一步校正杂波距离走动；当存在多个模糊数不同的目标时，可采用基于Clean思想的方法，逐个校正并检测各模糊数不同的目标。

［1］Klemm R K.Principles of space－time adaptive processing［M］.London：The Institution of Electrical Engineers，2002：87－100.

［2］吴仁彪.机载相控阵雷达空时二维自适应滤波的理论与实现［D］.西安：西安电子科技大学，1993：9－21.Wu Renbiao.Space－time adaptive processing for airborne phased array radar：theory and implementation［D］.Xi′an，China：Xidian University，1993：9－21.

［3］Wang H S C.Mainlobe clutter cancellation by DPCA for space－based radars ［J］.1991IEEE Aerospace Applications Conference Digest，1991，28 （33）：1－128.

［4］王永良，彭应宁.空时自适应信号处理［M］.北京：清华大学出版社，2000：26－43.Wang Yongliang，Peng Yingning.Space time adaptive processing［M］.Beijing：Tsinghua University Press，2000：26－43.

［5］Brennan L E，Reed I S.Theory of adaptive radar［J］.IEEE Trans on Aerosp Electron Syst，1973，9：237－252.

［6］Klemm R.Introduction to space－time adaptive processing［J］.Electronics ＆Communication Engineering Journal，1999，2（5）：5－12.

［7］Ward J.Space－time adaptive processing for airborne radar［R］.Technical Report 1015，MIT Lincoln laboratory，1994.

［8］Dipietro R C.Extended factored space－time processing for airborne radar systems［C］∥Proceeding of the 26th Asilomar Conference on Signal，System，and Computers.1992：425－430.

［9］保铮，廖桂生，吴仁彪，等，相控阵机载雷达杂波抑制的时－空二维自适应滤波［J］.电子学报，1993，2（1）：1－7.Bao Zheng，Liao Guisheng，Wu Renbiao，et al.Adaptive spatial－temporal processing for airborne radars［J］.Acta Electronica Sinica，1993，2（1）：1－7.

［10］Barbarossa Sergio，Farina Alfonso.Space－time－frequency processing of synthetic aperture radar signal［J］.IEEE Trans Aerospace and Electronic Systems，1999，30（2）：341－358.

［11］张顺生，曾涛，邢孟道.基于Keystone变换的微弱目标检测［J］.电子学报，2005，33（9）：1675－1678.Zhang Shunsheng，Zeng Tao，Xing Mengdao.Weak target detection based on Keystone transform ［J］.Acta Electronica Sinica，2005，33（9）：1675－1678.

［12］Perry R P，Dipietro R C，Fante R L.SAR imaging of moving targets［J］.IEEE Transactions on Aerospace and Electronics Systems，1999，35（1）：188－200.

［13］原浩娟，高梅国，姜伟，等.基于Knab内插核的Keystone变换［J］.数据采集与处理，2010，25（4）：425－429.Yuan Haojuan，Gao Meiguo，Jiang Wei，et al.Keystone transform Using Knab interpolation kernel［J］.Journal of Data Acquisition ＆Processing，2010，25（4）：425－429.

［14］Xing Mengdao，Wu Renbiao.Migration through resolution cell compensation in ISAR imaging［J］.IEEE Geoscience and Remote Sensing Letters，2004，1（2）：141－144.

［15］Li Y，Wu R，Xing M，et al.Inverse synthetic aperture radar imaging of ship target with complex motion［J］.IET Radar Sonar Navig，2008，2（6）：395－403.

［16］Zhou F，Wu R，Xing M，et al.Approach for single channel SAR ground moving target imaging and motion parameter estimation ［J］.IET Radar Sonar Navig，2007，1（1）：59－66.

［17］Fienup J R.Detecting moving targets in SAR imagery by focusing ［J］.IEEE Trans Aerosp Electron Syst，2001，37（3）：794－809.

［18］朱圣棋，廖桂生，周争光，等.机载双通道SAR地面慢速运动目标参数估计方法［J］.系统工程与电子技术2009，31（12）：2048－2052.Zhu Shengqi，Liao Guisheng，Zhou Zhengguang，et al.Approach to ground slowly moving target parameter estimation for airborne dual－channel SAR system［J］.Systems Engineering and Electronic，2009，31（12）：2048－2052.

［19］Zhang S，Zeng T，Long T，et al.Dim target detec－tion based on Keystone transformation［C］∥IEEE 2005International Radar Conference，2005（9－12）：889－894.

［20］Zhou Zhi，Su Zhigang，Wu Renbiao.Method for detecting ground moving target with range migration［C］∥IET International Radar Conference.Guillin，China：［s.n.］，2009：1－4.

［21］Wu Renbian，Jia Qiongqiong，Li Hai.A novel STAP method for the detection of fast dim air moving targets［C］∥IEEE International Conference on Signal Processing.Beijing，China：［s.n.］，2010：2160－2163.

［22］吴仁彪，贾琼琼，李海.机载雷达高速空中微弱动目标检测新方法［J］.电子与信息学报，2011，33（6）：1459－1464.Wu Renbiao，Jia Qiongqiong，Li Hai.Detection of fast moving dim targets on airborne radar via STAP［J］.Journal of Electronics ＆Information Technology，2011，33（6）：1459－1464.

［23］王冬梅.机载雷达空中机动目标检测［D］.北京：中国民航大学，2010：27－33.Wang Dongmei.Maneuvering target detection on the airborne radar［D］.Beijing：Civil Aviation University of China，2010：27－33.

［24］Jia Q Q，Wu R B，Li H.Impacts of Keystone formatting on space－time adaptive processing in airborne radar［C］∥IEEE International Conference on Signal Processing.Beijing，China：［s.n.］，2010：2164－2167.