个人外汇市场最优组合研究——基于Markowitz均值方差组合模型

林应诚

（安徽财经大学国际经济贸易学院，安徽蚌埠 233030）

一、国内外研究现状

国外对投资产品选择理论的研究起始于1952年，由Markowitz Harry教授最早系统提出现代资产组合理论的概念，此前的投资大多针对个别投资对象，Markowitz Harry(1952)首次提出在投资中需要保持“高收益”和“确定收益”两个风险因素的平衡，分别用期望收益率和收益率方差来衡量收益率水平和不确定性，建立均值—方差模型，主张分散化投资来规避风险，[1]即“不要把鸡蛋放到同一个篮子里”。但Markowitz Harry提供的方法面临的样本量和计算量巨大，随着投资产品种类增多，其实用性也受到质疑。在此之后，William Shape(1963)提出建立“单因素模型”来简化计算，考察相应指数对受益变化的影响。[2]这一简化形式使得现代资产组合理论应用起来更为实际。Treynor Jack(1961)、Treynor Jack(1962)、William Shape(1964)、Lintner John(1965)和Jan Mossin(1966)通过对现代资产组合理论的衍生性研究，形成了著名的资本资产定价模型(CAPM),该模型主要研究资产的预期收益率与风险资产之间的关系，以及均衡价格是如何形成的，认为期望收益率由无风险利率和风险溢价组成，并以β系数衡量投资产品或组合的市场风险。[3]-[7]此后，Ross Stephen(1977)突破性的发展了CAPM，提出套利定价模型（APT），APT用套利概念定义均衡，不需要市场组合的存在性，所需的假设也比CAPM更少、更合理。[8]

国内对外汇投资产品选择的理论的研究起步较晚，徐焱，荣喜民(2003)运用Markowitz组合证券投资理论讨论了外汇投资组合的选择和外汇储备的最优调整模型，并给出了最优组合投资及最佳调整策略，结合历史资料分别进行了计算和分析。[9]张岩（2008）改进了均值—方差模型，运用ARMA-ARCH时间序列数据模型，分析了其中外币的滞后特征，为投资者规避外汇汇率风险，实现投资收益提供了现实意义。[10]赵永秀(2005)从总体上介绍个人投资理财的心理准备和理财规划，然后分门别类地介绍银行储蓄理财、证券投资、房产投资、保险投资、黄金珠宝投资、收藏品投资等理财领域和财技。[11]

本文将基于我国个人外汇市场投资产品现状，将外汇汇率引入Markowitz的均值方差模型，探讨个人外汇市场投资的最优模型及其影响因素，并结合实际案例研究分析。

二、我国个人外汇市场投资现状

据中国人民银行统计，2012年我国外汇储量总额为236669.93亿元人民币，较2011年的232388.73亿元增长了约1.84%，随着的居民外汇持有量的增加，外汇投资备受关注，逐渐成为除股票和债券之外最普遍的投资方式。自2005年7月21日中国人民银行实行汇改之后，个人外汇投资渠道逐渐多样化，现有的个人外汇投资渠道有外币存款、商业银行外币理财产品、QDII产品、投资B股、外汇掉期和远期外汇、外汇期权、外汇保证金交易、购买外汇保单、货币兑换等。[12]其中前四种投资方式在国内较为流行。因银行理财产品和QDII产品特征上有诸多相似，可以比较这四类产品的特征如表1所示。

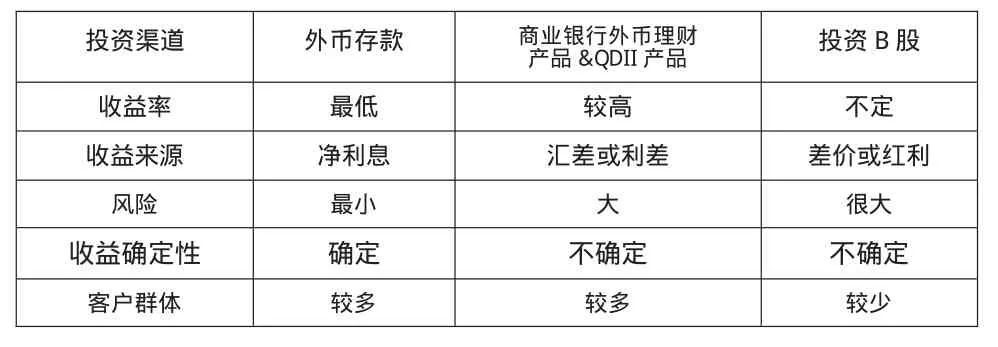
表1 个人外汇投资产品比较

三、Markowitz个人外汇市场投资组合模型的构建和分析

（一）模型假设

1.外汇投资市场是完全竞争市场，信息是完全的，外汇可以自由流动，买卖者众多。

2.投资者的决定仅仅依据外汇产品的收益和风险。即外汇组合的期望收益率和方差。

3.一种货币只有一种外汇产品，即外汇产品相对于币种是独一无二的，市场上有N种产品，且外汇市场不允许卖空。

4.总投资额用本币表示，外汇产品投资额用外币表示。

（二）符号说明

（三）模型构建

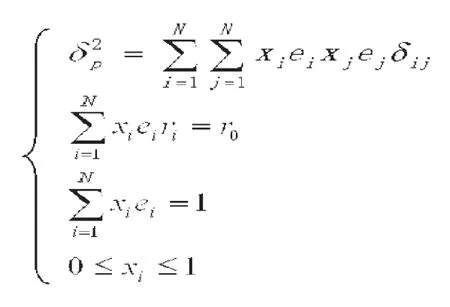
因此，构建该方程组的拉格朗日函数求解，具体如下：

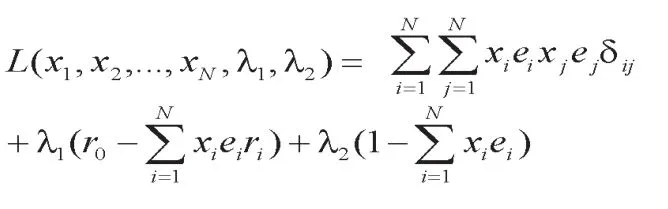
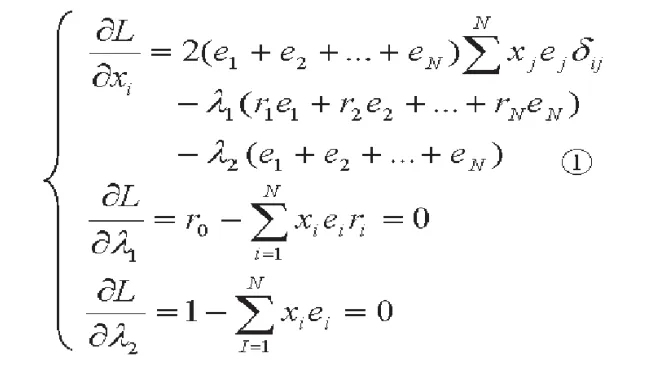
利用矩阵变换，将方程组中的①常数项（e1＋e2＋…＋eN）消掉，并拆分成方程组，得：

（四）模型结果分析

模型计算结果显示在一种外币对应一种外汇产品的个人外汇投资市场上，获得最优投资组合即收益最大或风险最小的条件是外汇汇率与投资比重成反比，外汇汇率上升时应该降低此外汇产品的投资比重，反之，则增加该外汇产品在投资组合中的比重。

四、案例分析

本文选取2013年1月1日至2013年4月30日共100天内美元、欧元、日元、英镑、澳元、港币六种外币每日收盘价作为原始数据，并计算日收益率的七天平均值作为相应的周收益率，日收益率计算公式如下：

其中et为日本外币市场汇率，et-1为上一日外币市场汇率。

用Eviews软件计算出周收益率协方差，为便于观察，将所得周收益率和周收益率的协方差数值都乘以100，以样本数据库中最后一周的周收益率代表预期的下一周收益率，得到期望收益表，如表2所示。

假设总投资额为10000元人民币，预期收益为100元人民币，即预期收益率1%，利用模型构建的方程组可以计算得到，不考虑其他外汇和交易条件，可以得到2013年4月30日各种外汇的最优投资组合，如表3所示。

表2 期望收益表

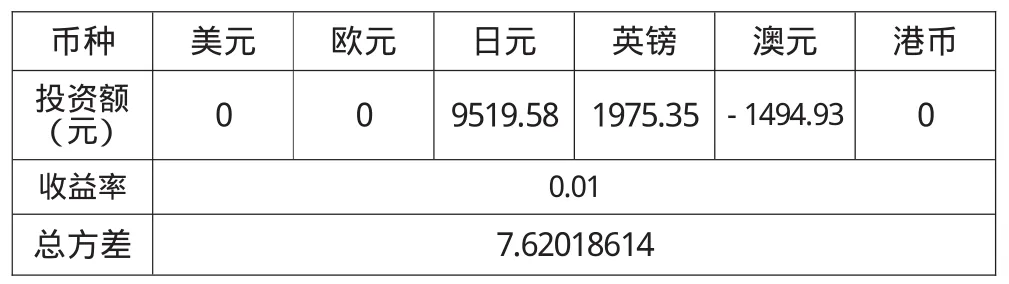
表3 最优外汇投资表

五、结论与展望

本文将外汇汇率引入Markowitz均值方差模型，构建最优外汇投资组合，有助于个人投资者规避外汇市场风险，实现收益最大化，有效杜绝了主观决策和非理性判断，对于实现外汇投资产品结构的量化分析具有重大意义，但由于Markowitz的均值方差模型使用选定的样本均值和方差预测预期数值，当模型应用于高频金融数据时，容易造成对预期值度量的偏差，加之模型假设条件的限制，模型的实用性稍显不足，这也是模型日后需要进一步改进的地方。

[1]Markowitz Harry.Portfolio Selection[J].The journal of Finance,1952,(1):77-91.

[2]William Shape.A Simplified Model for Portfolio Analysis[J].Management Science,1963,(2):277-293.

[3]William Sharpe.Capital asset prices:A theory of market equilib rium under conditions of risk[J].Journal of Finance,1964,(3)：425-442.

[4]Treynor Jack.Market Value,Time,and Risk[M].Unpublished manuscript,1961.

[5]Treynor Jack.Toward a Theory of Market Value of Risky Assets[M].Unpublished manuscript,1962.

[6]Lintner John.The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets[J].Re view of Economics and Statistics,1965,(1)：13-37.

[7]Jan Mossin.Equilibrium in a Capital Asset Market[J].Econo metrica,1966,(4)：768–783.

[8]Ross Stephen.The Capital Asset Pricing Model(CAPM),Shortsale Restrictions and Related Issues[J].Journal of Finance,1977,(1):177-183.

[9]徐焱,荣喜民.最优外汇组合投资及管理[J].天津轻工业学院学报,2003,(18):29-32.

[10]张岩.外汇投资组合决策研究[D].天津财经大学,2008.

[11]赵永秀.个人理财[M].深圳:海天出版社,2005.

[12]韩复龄.外汇交易工具与避险操作[M].北京:中国时代经济出版社,2006.