导流隧洞施工工期的模糊类比预测与评价方法研究

王仁超，周洪利

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

1 研究背景

工程施工工期确定方法有经验拟定法、工期定额法、网络进度法、工程类比法、模拟统计分析法等。其中，依据工程师经验的经验拟定法和工程类比法常常采用，属于定性分析法;工期定额法、网络进度法和模拟统计法属于定量分析法。但是由于制约工程施工工期的因素多样化以及某些因素具有不确定性、随机性，单纯的定性分析和定量分析均具有一定的限制性。定性与定量分析相结合方法是预测和评价工程合理工期的最好方法。实现定性和定量相结合，无疑模糊数学是一个较好的途径。例如在确定导流方式［1］，合理确定项目工期［2］、矿井建设工期预测［3］等诸多工程问题上成功应用了模糊数学方法。

隧洞导流作为水利水电工程施工导流常见的一种方式，近些年在许多大型水电工程中得到广泛的采用，而且导流隧洞施工往往处在施工进度的关键路径上，具有举足轻重的作用，因而确保导流隧洞施工工期的合理性和可行性具有重要意义。

导流隧洞施工工期与导流隧洞的规模、地质与水文地质、施工方法、施工队伍水平等诸多因素有关，其中地质与水文地质、工程施工队伍水平等因素具有不确定性和模糊性，施工环境因素具有随机性。

本文运用工程类比思想和模糊数学方法，在综合分析导流隧洞施工工期影响因素基础上，利用基于模糊因果聚类的模糊预测方法，通过对已建典型水电工程导流隧洞按工期进行聚类，实现了对拟建工程工期的模糊预测与评价。应用案例分析表明:本文提出的方法可以较好地预测和评价导流隧洞施工工期的合理性。

2 导流洞施工工期影响因素分析

工程合理施工工期是指工程自开工之日起至按工程合同完成约定的全部工程内容，综合考虑工程规模、工程结构形式、施工环境、地理位置以及施工单位资质条件、资金、人员、材料、设备力量等各方面的因素，以达到符合合同约定竣工验收条件，提交竣工验收申请报告之日止的持续施工时间。工程施工中常用的工期有合理工期、经济工期。合理工期不同于经济工期。经济工期仅与工程施工成本费用有关，因此，其概念是清晰的，确定方法也是非常直接的。从合理工期的定义可以看出:合理工期与工程规模、工程结构形式、施工环境、地理位置以及施工单位资质条件、资金、人员、材料、设备力量等各诸多方面的因素有关，且合理工期与这些因素之间的关系具有非线性、不确定性，其中某些因素本身就具有模糊性，因此，合理工期也具有一定的不确定性、模糊性和相对性。

具体而言，对我国大型水电站建设的研究发现，导流洞的建设多出于关键路径上，而且导流洞却应用于地势比较狭窄的地带，具有地质条件复杂，施工工期紧，工程量大，施工强度高等特点，影响施工的因素众多，是一项非常复杂的施工过程。因此施工工期总会受各种因素的制约和影响，综合考虑大致可以分为确定性因素和不确定性因素等，具体可见图1所示。

图1 影响施工工期因素图Fig.1 Factors affecting the construction period

确定性因素:确定性因素是指针对任何具体的实际工程，无论什么情况下，该种因素与施工工期构成一种稳定的因果关系，正是由于这种确定性因素的存在，才使得工程施工工期具有客观性、可预测性和基本稳定性。水利工程导流隧洞施工，决定施工工期的确定性因素主要体现在工程类型及工程规模方面。

不确定性因素:工程项目，尤其大中型项目是一项极其复杂的系统工程，施工进度必受到多种因素的制约，影响施工工期的不确定因素也必然存在，并且此类因素具有很强的随机性、偶然性和模糊性。影响导流隧洞施工工期的不确定因素则又可以分为随机因素和模糊因素。随机因素是指在工程建设过程中可以预知的结果，但不知道是哪些结果，所以往往具有动态性，不利于控制。随机性因素主要体现在施工过程中出现的意外情况，比如不利于施工的气象条件，施工机械出现故障，材料堆放不合理等。

在影响施工工期的因素中，除确定性因素和随机性因素外，不可预见的地质条件、地质资料勘探等对工期具有明显的影响［4］。导流洞所处地质条件的围岩类别及分布在很大程度上存在着模糊性和不确定性。另外，施工经验、机械设备的配置、管理水平等其他模糊因素对施工工期也会造成影响。

只有充分认识确定性和不确定性因素对施工工期带来的不同影响，才能对隧洞施工工期做科学预测，并对进度计划做统筹控制，编制合理的施工组织设计方案，为预测和评价合理工期提供理论依据，应对和处理突发情况。

3 施工工期预测原理及步骤

导流隧洞施工工期的模糊预测及类比评价是指在确定类比指标体系的前提下，选取若干已建导流隧洞作为研究样本和类比对象，采用基于因果聚类的模糊预测方法对研究样本作模糊聚类，在最佳聚类的基础上对拟建工程的导流洞施工工期做出预测并基于最相似工程案例予以评价。

3.1 类比评价指标的确定原则

类比评价指标是所选工程案例划分类别并对被预测对象进行参数预测与评价的前提。类比评价指标体系的确定需要遵循以下几点原则:①应是具有较强分辨力和代表性的特征参数;②所选指标应具有独立的物理意义，符合科学、可比、可测和简明的特点;③对导流洞施工工期具有客观明显影响性;④以已建导流洞的实践为参考，进行综合分析比较，搞清楚拟建导流洞的基本情况;⑤最终确定的类比评价指标体系在必要时可以进行修正。

3.2 样本聚类分析

样本的聚类分析是指按照一定的准则确定最佳分类结果，每一类中的样本都具有相似性、可比性和参考性。自1965年美国数学家L.A ZADEH创立模糊集合论后，又于1969年E.H RUSPINID引入了模糊划分的概念进行模糊聚类分析［5］。模糊聚类分析是在模式识别、医学、化学、农业等不同的学科和专业领域中经常采用的一种方法。它是研究事物分类的一种多元分析方法，能够很好地处理多样本分类问题，在无任何专家经验的基础上，也能够给出各个样本之间的关系。最终，确定样本的亲疏程度而实现分类。

运用模糊聚类分析方法解决工程实际问题，一般遵循以下几个步骤［6］:

(1)结合工程案例类比思想，根据类比指标体系确定原则建立统计指标，并选择需要聚类分析的样本［7］;

(2)为保证具有不同量纲的量能够进行比较，并且同时保证各统计指标数据在［0，1］区间上，对数据作标准化处理;

(3)对样本中的元素两两之间赋以区间［0，1］内的一个数，建立模糊相似矩阵;

(4)对模糊相似矩阵作计算处理，求得模糊等价矩阵;

(5)依据模糊等价矩阵，选取不同的截集水平对样本划分类别。

3.3 工期模糊预测方法

预测是对研究事物未知参数的估计，在工程应用中非常有必要并且意义重大。模糊预测是通过对以往类似工程的调查和分析，对拟建工程所求参数的定位，事先做出估计与评价。虽然拟建工程需要计算的指标参数有其自身的特点，但是建设的过程与其相似工程却有共通性，并且具有规律性，因此可以进行预测和类比评价。

模糊预测是建立在最佳聚类结果的前提下，建立特征模糊集，并利用专家打分法或层次分析法计算各类的特征模糊集的权重，最后构造以预测指标为参数的三角模糊数。最后，应用最大隶属度原则或择近原则方法，预测指标值。其计算步骤［8］如下:

(1)对作为研究样本的已建导流洞求得最佳聚类结果为

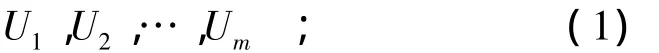
(2)建立模糊特征集

其中(ω1，ω2，…，ωn)为各指标的权重，由层次分析法求得。

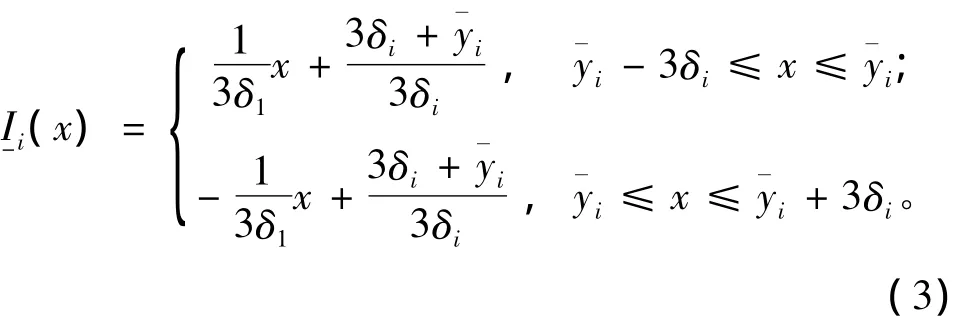
(4)模糊预测。假定对样本s的量α进行预测。如果s的状态因素是一个确定的点xs∈X，那么，对用“最大隶属度原则”，选出Pi0，然后以相应的Ii0作为样本s的量α的模糊预测值。

3.4 工程案例类比评价

工程案例类比法是指对实际工程案例进行深入系统的研究，通过对工程案例的描述，概况总结能够反映工程案例的若干工程特征作为类比的案例属性，在相同案例属性的基础上并对其赋以权重值，利用相关方法寻找与拟建工程比较类似的1个或几个工程案例，最终得出相似结论并对其他相关方面就相似或相同性进行合理的推理和评价。

本文将模糊数学理论与工程案例类比相结合，利用模糊聚类分析方法首先将研究样本依据相似程度划分类别，每一类中的几个样本都具有极高的可比性，然后在模糊预测过程中依据最大隶属度原则确定与被预测对象最为相似的样本所属类，最终根据最相似工程案例的实际情况对拟建工程就施工工期长短及在施工进度计划中的安排进行合理性评价。

4 实例分析

4.1 工期预测

本案例主要结合二滩、小湾、溪洛渡等3个已建工程的10条导流隧洞作为研究对象，充分考虑影响导流隧洞施工工期的各个因素，依照类比评价指标集的确定原则以及工程案例类比思想，选取合适的类比评价指标。由于评价指标集中随机因素在工程实施过程中的随机性比较大，因此忽略此类因素的影响。3个工程导流洞建设单位的施工经验和水平是相对发达和先进的，因此对工期的影响性比较接近。综上所述，根据类比评价指标集的确定原则并结合具体工程的实际条件，选取类比评价指标如表1。

表1 类比评价指标Table 1 Analogy evaluation indexes

4.2 建立样本指标矩阵

选取二滩、小湾、溪洛渡3个已建工程的10条导流洞作为研究样本。各样本的评价指标值如表2所示。

表2 样本类比评价指标值Table 2 Index values of the analogy evaluation of samples

该实例将导流隧洞的施工工期作为预测评价指标，并以各个样本的实际施工工期为依据。具体工程样本的实际施工工期为

4.3 确定最佳聚类

为保证计算结果具有说服力，现分2种情况分别进行计算分析。

情况一:

以导流隧洞s10作为预测的对象，其余9条导流隧洞作为聚类样本。

以s1—s9九条导流洞为初始的样本矩阵S为

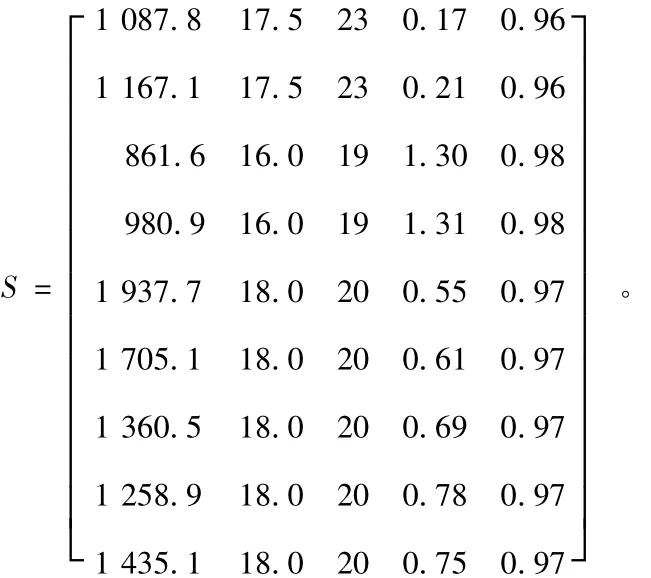
对初始样本矩阵做数据标准化、数据标定、传递闭包等计算，经历上述过程求得模糊等价矩阵T^1为

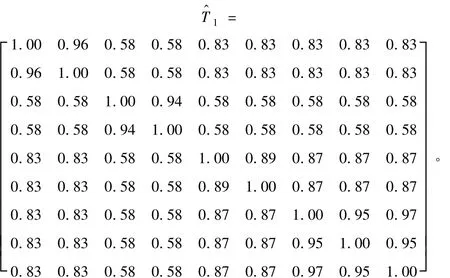
由于截集水平越小分类结果越模糊，截集水平越大分类结果越精确，故截集水平λ的值不宜过小或过大。根据经验，经多次试验取值最终确定截集水平λ=0.88，确定最佳聚类如下:

最佳聚类结果为:

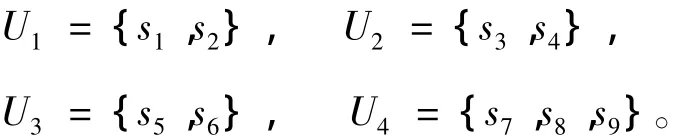
情况二:

以导流隧洞s9作为预测的对象，其余9条导流洞作为聚类样本。同理情况一求得最佳聚类结果为:

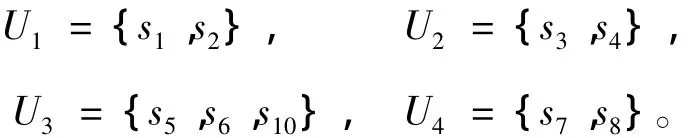
4.4 指标预测

情况一:

经模糊聚类分析后，最佳聚类结果为:

又有

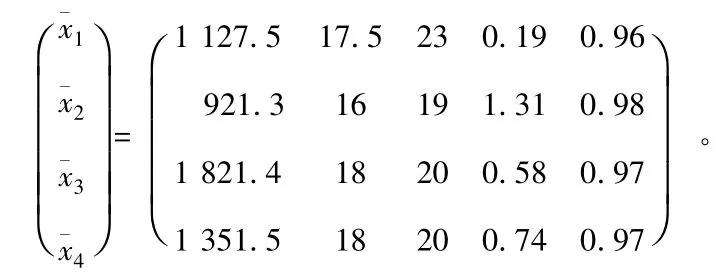
并且

经由层次分析法可求得各指标的权重为

则求得各类的特征模糊集为

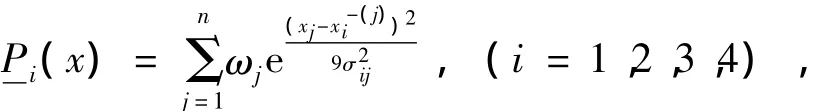
将 s10=(1 697.1，18，20，0.63，0.97)代入上式，计算得特征模糊集:由最大隶属度原则，应取对应的模糊数作为预测结果。

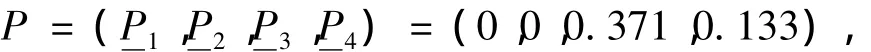
故导流隧洞10的预测工期应在33个月和33.5个月之间，取33.25个月的可能性最大。实际导流隧洞10的施工工期为33.5个月，所求结果与实际值非常接近。

同情况一的计算过程，可求得情况二时的特征模糊集为

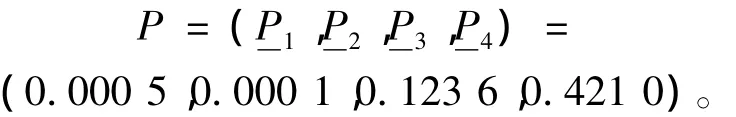
故导流隧洞九s9的预测工期应为31个月。实际导流隧洞9 s9的施工工期为31个月，所求结果与实际值完全吻合。

4.5 结果评价

经上述2种情况计算结果可以看出，预测结果与工程实际结果极为接近或相同，说明将工程案例类比思想与模糊数学的相关理论结合应用于工期预测中是可行的。那么，导流隧洞的施工进度计划是否合理呢?就情况一而看，样本s10的预测工期在33个月和33.5个月之间，由三角模糊数的隶属函数可得知s10的最可能取值为33.25个月。施工工期最短时当取值33个月，同时针对此案例而言，预测对象与样本s5最为相似，施工工期最长时当取值33.5个月，此时与s6最为相似。所以基于工程案例类比的思想，将预测对象在不同情况下与相似的2个样本进行类比。通过分析考虑样本s5，s6的具体施工情况，对于已建的s5，s6这2条导流隧洞在工期安排以及在整个施工进度计划中都是合理可行的，因此便可以大致地认为导流隧洞s10的施工工期是合理可行的。同理可分析得到情况二。

5 结论

通过以上基于因果聚类的模糊类比预测方法在导流隧洞施工工期预测和评价方面的初步应用研究，可以得到以下结论:

(1)本文综合分析影响导流洞施工工期的各个因素，从工程类比角度出发，建立了模糊类比评价指标体系，并将模糊数学理论应用到导流洞工期预测中。在工程实例应用中，情况一预测导流洞的工期为33.25个月，其实际工期为33.5个月，预测值与实际值非常接近，情况二预测导流洞工期为31个月，其实际工期为31个月，预测值与实际值完全吻合。2种情况下，证实本文提出的方法适用于导流洞工期预测。

(2)本文所求得的预测结果是建立在因果聚类的基础上，采用最大隶属度原则，故预测对象与特征集中最大特征数对应类中的样本具有最大相似度，因此与其具有可比性，并且可以作为对预测对象评价的依据。

［1］唐晓阳，冉崇辉.导流方式的模糊数学最佳选择［J］.水力发电，1997，(3):25－28.(TANG Xiao-yang，RAN Chong-hui.The Best Choice for Diversion Mode with the Help of Fuzzy Math［J］.Water Power，1997，(3):25－28.(in Chinese))

［2］谢忠镖.随机模糊方法研究合理确定工程项目工期［J］.数学的实践与认识，2006，36(10):41－45.(XIE Zhong-biao.Reasonable Determination of the Project Duration with Random Fuzzy Method［J］.Journal of Mathematics in Practice and Theory，2006，36(10):41－45.(in Chinese))

［3］张培建.模糊数学在矿井建设工期预测中的应用［J］.阜新矿业学院学报，1988，(增 1):28－33.(ZHANG Pei-jian.The Application of Fuzzy Mathematics in Mine Construction Period Forecast［J］.Journal of Fuxin Mining Institute，1988，(Sup.1):28－33.(in Chinese))

［4］张云波.工程项目工期延误原因分析［J］.华侨大学学报(自然科学版)，2003，24(4):369－373.(ZHANG Yun-bo.Reason Analysis of the Project Schedule Delays［J］.Journal of Huaqiao University(Natural Science)，2003，24(4):369－373.(in Chinese))

［5］孙 永.模糊聚类分析在机械故障诊断中应用评述［J］.云南农业大学学报，2008，23(5):698－700.(SUN Yong.The Application Comments in Machine Fault Diagnosis with Fuzzy Clustering Analysis［J］.Journal of Yunnan Agricultural University，2008，23(5):698－700.(in Chinese))

［6］许海洋，汪国安，王万森.模糊聚类分析在数据挖掘中的应用研究［J］.计算机工程与应用，2005，(17):177－179.(XUHai-yang，WANGGuo-an，WANGWansen.The Application Comments in Data Analysis［J］.Journal of Computer Engineering and Applications，2005，(17):177－179.(in Chinese))

［7］张 勤.模糊数学在工程地质类比中的应用［J］.河海大学学报，1990，18(4):1－5.(ZHANG Qin.The Application of Fuzzy Mathematics in Engineering Geological Analogy［J］.Journal of Hohai University，1990，18(4):1－5.(in Chinese))

［8］麻兴斌，唐林炜.基于因果聚类和模式识别的模糊预测方法及其应用［J］.山东科技大学学报，2004，23(1):76－79.(MA Xing-bin，TANG Lin-wei.Fuzzy Prediction Method and Its Application Based on Causal Clustering and Pattern Recognition［J］.Journal of Shandong Science and Technology University，2004，23(1):76－79.(in Chinese))