不平衡推力迭代法的改进
2013-11-13蔺宗宗
李 博,蔺宗宗,杨 柳
(兰州大学土木工程与力学学院,兰州 730000)
1 研究背景
不平衡推力法又称传递系数法或剩余推力法,是我国学者提出的一种边坡稳定性分析方法[1]。不平衡推力法是我国工民建和铁道部门在核算滑坡稳定性时使用非常广泛的方法,适用于任意形状的滑裂面[2]。由于该法能够计及土条界面上的剪力的影响,可以获得任意形状滑动面在复杂荷载作用下的滑坡推力,且计算简洁,具有适用且方便的优点[3]。但其分析结果在某些情况下会产生很大的误差,近年来不少学者对不平衡推力法做了改进,李建明[4]通过变倾角的方式对传递系数法(不平衡推力法)做了改进,并对条间作用力的倾角大小进行了定量化,但其定量的准确程度尚未可知。何木、赵其华[5]则通过对方向角的修正来改进传递系数法(不平衡推力法),其计算原理是考虑边坡整体的力矩平衡,但传递系数法在无附加荷载情况下自动满足整体力矩平衡[1],因此本文也是基于对方向角的修正,对不平衡推力迭代法进行了改进。
2 不平衡推力迭代法的基本原理
根据姜德义等[6]编写的《边坡稳定性分析与滑坡防治》书中介绍的不平衡推力迭代法,其基本原理如图1。
图1表示有n个块体,各块体作用力如图1所示。第i块体倾角为αi,块体上作用力分别为T'i,Ni,Wi,各块体相应滑动面均已处于极限平衡状态。设第i-1块体对第i块体的不平衡推力为Pi-1,其作用力方向与第i-1滑动面平行。
对于第i块体,在极限状态下时可由抗滑力等于下滑力,计算出不平衡推力Pi;同理,通过对第n块体的受力分析,可求得稳定系数的表达式,这样就可以得出稳定系数了。
其计算步骤为:首先要假定n为某一值,利用Pi表达式,按照i=1,2,…,n分别求出各块体间的不平衡推力,将所求得的Pn-1代入到稳定系数表达式中,即可计算出稳定系数n。如果假定的n值与所求得的n值相差很大,可利用计算所得的n值重新计算各块体间不平衡推力Pn-1,将所求得的Pn-1代入到稳定系数表达式,求得稳定系数n。如果相差仍很大,不满足要求时,应重复上述步骤逐次迭代,直到2次所得值相差在一定范围内为止,这时所得n值即为所求稳定系数大小。
当然,也可通过相关计算机程序求解,从而更加快速地计算出n值。

图1 不平衡迭代法计算示意图Fig.1 Schematic of calculating unbalanced thrust force using iterative method
3 基于方向角修正的不平衡推力迭代法的改进
3.1 不考虑地震力条件下的改进
传递系数法中假设第i块体对第i+1块体的不平衡推力Pi的作用方向与第i滑动面平行,这与实际情况是有出入的,所得出的稳定系数与实际情况会有误差存在。为了尽可能地减小误差,何木、赵其华[5]对传递系数法进行了改进,其基于对方向角的修正,通过工程实例验算结果表明,改进后较传统传递算法更精确,物理过程更合理,且可以满足工程精度要求。通过边坡整体力矩平衡进行求解,由图解法可求得滑坡稳定性系数。
本文也是基于对方向角的修正,对不平衡推力迭代法做了改进,推导出计算滑坡稳定系数的公式。
设第i-1块体对第i块体的不平衡推力为Pi-1,作用方向为第i-1块体滑动面与水平方向夹角的λ 倍(λ=0.1,0.2,…,1.5,1.6),为λαi-1,对于第i块体,其抗滑力与下滑力分别为:

根据垂直于滑动面上的平衡关系可得
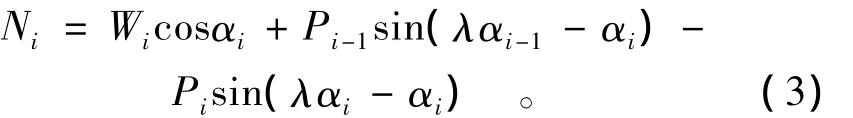
由块体上抗滑力与下滑力相等,即T'=T,可得

式(1)至(3)中:n为假定的滑坡稳定系数;i为块体编号;λ为方向角修正系数;T'为抗滑力;T为下滑力;T'i为极限平衡状态下第i块体滑动面上的抗滑力;Pi-1,Pi分别为第 i-1块体、第i块体所受法向支持力;αi-1,αi分别为第 i-1 块体、第 i块体的方向角;Ci为第i块体滑动面的内聚力;Si为第i块体滑动面的面积;fi为第i块体滑动面的内摩擦系数。
经过简化后可得
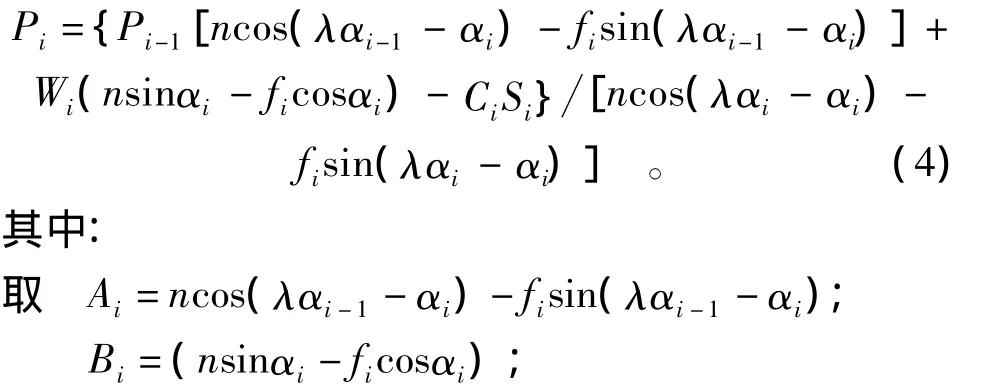

则(4)式可变为

第i块体的受力情况如图2所示。

图2 第i块体的受力示意图Fig.2 Schematic of forces acting on the i block
同理,第n块体的抗滑力等于下滑力,即

同理,由式(1),(2),(3)可得:

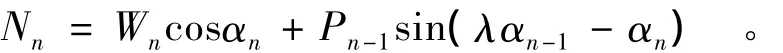
将 T,T'和Nn代入到T=T',化简后得

式(6)中n即为计算所得稳定系数。
第n块体的受力情况如图3所示。
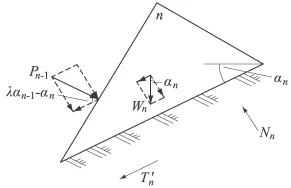
图3 第n块体的受力图Fig.3 Schematic of forces acting on the n block
3.2 考虑地震力的条件下的改进
对于第i块体,其抗滑力与下滑力分别为:

由抗滑力等于下滑力,即T'=T可得

式(7)中ks为水平地震影响系数;ksWi即为条块n中水平地震力大小。其中:

则(7)式可变为
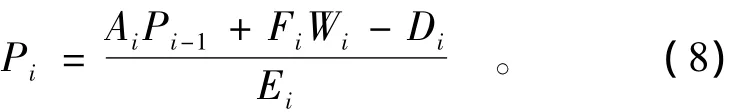
地震力条件下第i块体的受力情况如图4所示。

图4 地震力条件下第i块体的受力图Fig.4 Forces acting on the i block in the presence of earthquake force
同理,对于第n块体,其抗滑力和下滑力分别为:

其中

由 T=T',可得

地震力条件下第n块体的受力情况如图5所示。
该方法的计算模式是先假定λ的大小,其中λ=0.1,0.2,…,1.5,1.6,在计算中可中间插值,后续的具体计算步骤同改进前的方法。
4 工程应用
在文献[6]中,某边坡如图6所示,滑动土体根据滑动面形状可分为3个条块,各条块底面尺寸如图6所示。
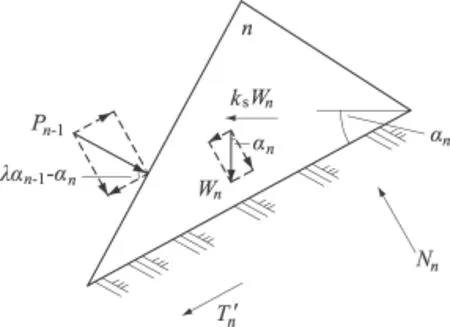
图5 地震力条件下第n块体的受力图Fig.5 Forces acting on the n block in the presence of earthquake force

图6 边坡剖面示意图Fig.6 Sketch of slope profile
4.1 边坡参数
据工程资料,边坡各条块的物理力学参数如下。
第1条块:

第2条块:

第3条块:

4.2 计算过程
由于推导后的公式中存在2个变量,分别是n和λ,如果采用手算,则计算过程过于复杂,因此,本文采用Visual Basic编程的方式解决。基于上述公式,以n和λ为自变量,首先找出合适的n值范围,在此范围内经过多次循环计算,由于程序编写中2个量不能用同一参数表示,因此,记带入n和λ后计算所得的n为x,以便于区分。经过循环计算,选取n的范围为0.9~1.0,再经过多次循环计算,即可求出稳定系数。当n=0.91时所得结果如表1。
在n=0.91,λ=1.217时,计算所得稳定系数为x=0.909 952 4,n与x最为接近。故最终的稳定系数的计算结果取为0.910。
4.3 结果分析
通过编程计算,其所得的结果表明,在λ=1.217的情况下,最终所得稳定系数为0.910,小于1,该边坡是不稳定的;当λ=1时,即为传统不平衡推力迭代法,通过计算可求得n=0.909;在姜德义、朱合华、杜云编写的《边坡稳定性分析与滑坡防治》一书中,取n=1.1,最终计算的不平衡推力大于0,边坡是不稳定的。

表1 不同λ值时的计算结果Table 1 Calculation results with differentλvalues
5 结论
(1)本文基于对滑块推力方向角的修正,对不平衡推力迭代法做了改进。论文中改进方法的推导过程是合理的,从理论上来说也是科学的,该方法具有一定的实用性,但尚需具体工程实例的验证。
(2)在具体算例的计算中,由于计算量较大,采用Visual Basic编程的方式进行计算,其结果表明利用改进后的方法比改进前的方法所得稳定系数偏大0.11%,二者是比较接近的。
(3)改进方法考虑了地震力作用的情况,使得应用范围更加广泛。
[1]孟庆银.用不平衡推力法快速计算边坡的稳定因数[J].土工基础,2010,24(6):53-55.(MENG Qingyin.Efficient Calculation of Slope Stability Factor with Unbalanced Thrust Force Method[J].Soil Engineering and Foundation,2010,24(6):53-55.(in Chinese))
[2]严绍军,唐辉明,项 伟.地下排水对滑坡稳定性影响动态研究[J].岩土力学,2008,29(6):1639-1643.(YAN Shao-jun,TANG Hui-ming,XIANG Wei.Study on Dynamics of Underground Drainage Effect on Landslide Stability[J].Rock and Soil Mechanics,2008,29(6):1639-1643.(in Chinese))
[3]张月英.基于改进不平衡推力模式的边坡稳定性分析及程序实现[D].长沙:湖南大学,2007.(ZHANG Yue-ying.Stability Analysis of Slope Based on Improved Imbalance Thrust Force Method and the Realization of Its Program[D].Changsha:Hunan University,2007.(in Chinese))
[4]李建明.变倾角传递系数法及其在水电站滑坡分析中的应用[J].水电站设计,2010,26(4):13-15,19.(LI Jian-ming.Variable Inclination Transfer Coefficient Method and Its Application in Landslide Analysis of Hydropower Station[J].Design of Hydroelectric Power Station,2010,26(4):13-15,19.(in Chinese))
[5]何 木,赵其华.基于方向角修正的改进传递系数法[J].地质灾害与环境保护,2010,21(1):79-82.(HE Mu,ZHAO Qi-hua.Improved Transfer Coefficient Method Based on Correcting Direction Angle[J].Journal of Geological Hazards and Environment Preservation,2010,21(1):79-82.(in Chinese))
[6]姜德义,朱合华,杜云贵.边坡稳定性分析与滑坡防治[M].重庆:重庆大学出版社,2005.(JIANG Deyi,ZHU He-hua,DU Yun-gui.Slope Stability Analysis and Landslide Control[M].Chongqing:Chongqing University Press,2005.(in Chinese))
