资源和环境约束下的共同物流运作风险SVM预测模型

周 敏，黄福华

(1．中南大学交通运输工程学院，湖南 长沙 410075;2．湖南商学院工商管理学院，湖南 长沙 410205)

一、文献综述

资源和环境是经济社会可持续发展的两大基础性要件和有力保障。我国是人口大国，也是资源消耗大国，近年来的“粗放式”发展模式严重超过了资源和环境的承载力，资源和环境正成为经济社会下一轮发展的重要瓶颈［1］。随着经济持续增长和城市化进程快速推进，人民生活水平日益提高，连锁超市、电视及网络购物等新型流通业态不断涌现，整个社会对物流服务规模和质量提出了更高的要求。从日本、德国等发达国家的发展经验来看，共同物流是提升物流效率、降低物流运作负面影响的有效方法之一。共同物流是经过长期发展和演变而形成的，是一种追求物流规模化和高效率的先进物流形式，对提高货车装载率、降低物流成本、缓解交通拥挤等方面具有重要意义［2］。

在资源和环境约束下，共同物流涉及主体多、运作环节多、各成员之间关系复杂，存在着较大的运作风险。国内外学者对共同物流的研究主要集中在共同物流内涵、运作形式、合作收益分配等方面［3］［4］，现有文献对共同物流运作风险研究以定性研究为主。关于风险评估的方法主要包括AHP 法、Fuzzy 法、OCTAVE 法、CORAS 法、PRA 法、ANN 法、综合分析法等［6］［7］［8］［9］［10］［11］，从定性或定量角度对物流企业进行风险评估。

定性分析无法给出风险的定量度量值，难以真实度量风险大小。现有的定量评估方法虽能对风险进行定量评估，但实施过于烦琐，而且数据需要人工整理，容易出错，不适应共同物流动态变化的特点。为提高共同物流运作风险评估的可信性和可操作性，本文提出基于支持向量机(support vector machine，SVM)的共同物流运作风险评估模型，并对共同物流运作风险进行科学预测。

二、资源和环境约束下的共同物流运作风险评价指标

本文采用模糊综合评价法，将定性与定量相结合，通过量化决策者的经验判断，使模糊概念具体化;解决结构复杂且缺乏数据的共同物流风险预测问题，相应得到的数学结果又能通过一定的方法转为语言描述，客观有效地描述指标体系反映的性质，有利于考察指标对最终风险的影响程度［12］。综合前人研究成果，本文将共同物流运作风险影响因素归纳成15项评价指标，以对共同物流运作风险水平进行评估:(1)合作伙伴能力风险;(2)质量风险;(3)道德信用风险;(4)物流与库存控制风险;(5)内耗风险;(6)信息传递风险;(7)信息技术与安全风险;(8)约束风险;(9)库存风险;(10)柔性风险;(11)价格波动风险;(12)政策与法律风险;(13)需求不确定性风险;(14)自然灾害风险;(15)社会环境风险。我们将可以量化的指标归一化处理，将不能量化的指标划分为5个级别——高、较高、一般、较低和低，其对应值分别为0.9、0.7、0.5、0.3、0.1。采用多位专家打分取平均的方法获得原始值，并进行归一化处理。假设总共有样本M个，每一个样本的每一个风险指标由N位专家打分，第m个样本的第i个指标平均得分Pm，i为:

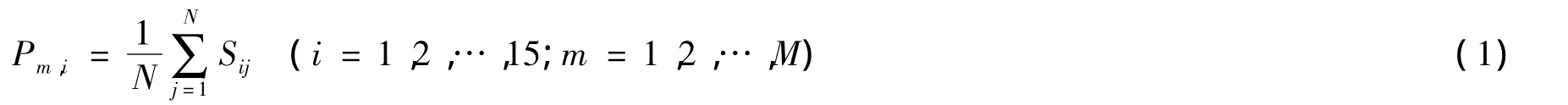
其中，Sij表示第j个专家对第i个指标打分的分值。我们把15个风险指标转化成1×15维行向量，即

三、SVM工作机理与共同物流风险预测步骤

(一)SVM基本原理

20世纪70年代末期，Vapnik等提出了一种新的神经网络——支持向量机。支持向量机通过某种事先选择的非线性映像 (核函数)将输入向量映像到一个高维特征空间，在这个空间中构造最优分类超平面。

图1中的圆圈和正方形分别代表两类样本，利用SVM方法将两类样本分开的基本思想就是寻找一条最优分类线H:wx+b=0(w为权变量)，从而把样本分为两部分，在H1、H2上的黑色样本为支持向量(SV，Support Vector)。将这一原理推广到高维空间中，如果两类样本可以被一平面正确分开且分类间隔最大，则图1中的最优分类线H就将扩展成为高维空间中的最优超平面(Optimal Separating Hyper-plane，OSH)。

考虑分类问题，根据给定的训练集T

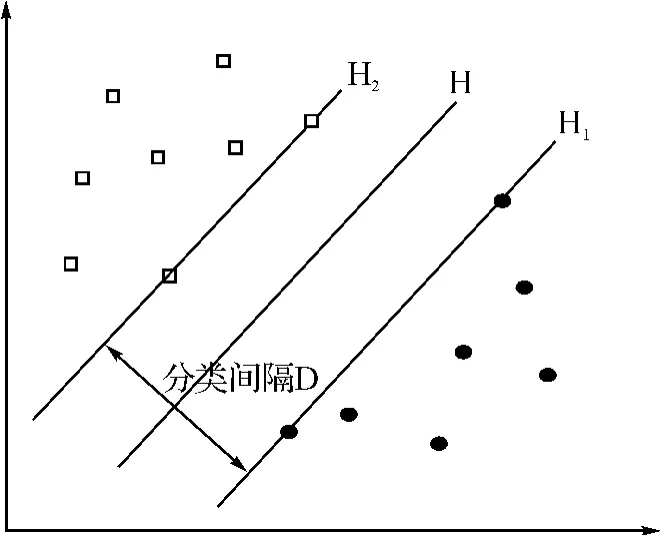
图1 利用SVM方法解决分类问题的基本原理

T={(x1，y1)，…，(xl，yl)}∈(X × Y)l(xl∈X=Rn，yl∈Y={1， －1}且 i=1，2，…，l)

分类问题需要寻找决策函数f(x)=sgn(g(x))，以便能推断任一模式条件下x相对应的y值。高维空间线性条件下的最优分类函数(即SVM决策函数)为:

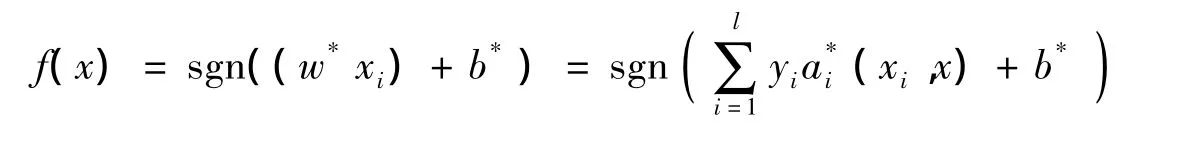
由于共同物流运作风险涉及因素多，且各因素之间存在复杂的非线性关系，因而本文采用非线性分类学习机。非线性分类学习机只需要在线性学习机基础上引入一种核函数K(x，xj)满足Mercer条件，即可将其转化为高维空间中的线性问题，这里采用径向基核函数:

通过改变σ和其他参数可以改善SVM的预测性能，直到最优效果为止。

(二)基于SVM的共同物流风险预测步骤

利用SVM方法进行共同物流风险评价的核心是要建立一个训练样本集，通过确定合适的核函数及参数，对已知样本集进行学习与训练，最后确定最优决策函数，并利用该函数进行风险评价和预测。SVM共同物流风险评价方法主要遵循以下的基本程序与步骤。

首先，为提高建模精度，本文采用如下方法进行预处理:

对于所有时间序列，取前面r个数值作为训练建模样本，其余的作为测试样本。为更有效地利用有限的数据，我们对其进行相空间重构，即将一维的实践序列转换为矩阵形式，以尽可能地挖掘数据的信息量。于是，我们得到用于向量机学习的样本，建立映射f:Rm→R。对于学习样本，我们按照如下的回归函数进行训练:

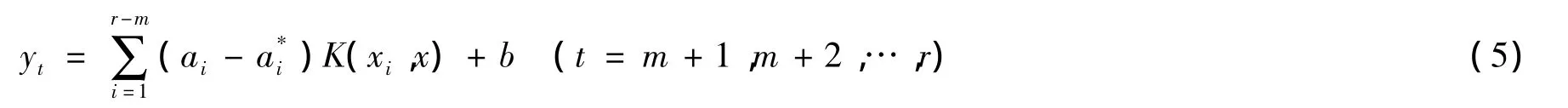
其中，ai，a*i为拉格朗日乘子，b为分类面阈值。

为了方便评价预测方法的准确性，我们引入均方误差MSE和均等系数EC两个指标:

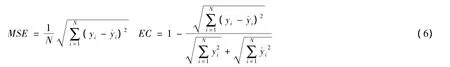
均值系数可形象地描述预测值和实际值的拟合度。一般地，拟合度在0.9以上可认定为较好的拟合。这两类指标分别从逐点比较和整体预测趋势两方面对预测方法进行评价，从而较为全面地判断预测的准确性。

四、实例分析与结论

(一)数据采集

首先，组建样本训练集。选择16个中部地区不同区县建立共同物流体系的样本，即湖南省(3个)、湖北省(3个)、河南省(3个)、山西省(2个)、安徽(3个)、江西省(2个)，并随机编号。将样本分为两类，序号1－12的12个企业作为训练样本，13－16的4个企业作为预测检验样本。经过标准化数据及其风险等级后组成训练集，其中评价指标值作为输入变量，风险等级为输出变量，归一化处理后得到的整个风险指标矩阵如表1所示。

(二)实例分析

本文将共同物流运作风险划分为5个级别——低(L)、中低(ML)、中等(M)、中高(MH)、高(H)，风险级别对应值分别为 ［0，0.2］、(0.2，0.4］、(0.4，0.6］、(0.6，0.8］、(0.8，1］。选择MATLAB 2010的SVM平台对我国典型共同物流运营风险进行评价。调用统一编辑的样本数据，选择径向基核函数，选取参数C=100和g=0.001，进行建模运算。

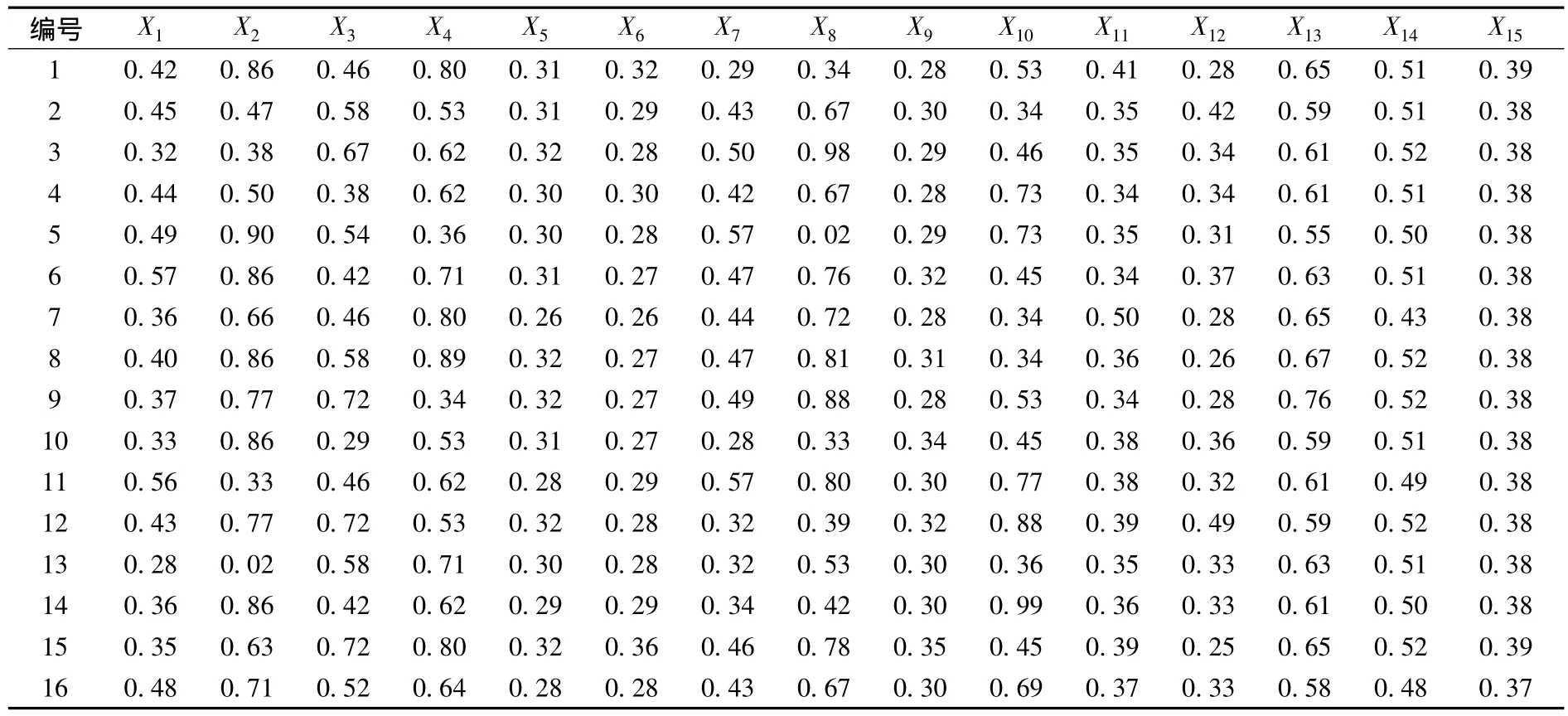
表1 2011年中部地区典型区县共同物流运作风险评价指标数据归一化处理

经过训练后，对序号为13－16号企业进行了分类预测，其首次分类预测结果如表2所示。采用SVM方法对典型共同物流运作风险评估后的结果如表3所示。

表2 基于SVM的典型共同物流运作风险等级测试结果

表3 基于SVM的典型共同物流运作风险等级

随着信号原始数据的不断丰富，相点密度会不断增大，预测值也将更趋于合理可信，从而有助于预测精度的提高。误差评价指标如表2所示，均方误差为2.67%，而均等系数为96.79%，达到了很高的拟合度，说明预测结果有较强的可信度。

五、结 论

通过对资源和环境约束下的中部地区典型区县共同物流运作风险分析及评价的研究，本文得出以下结论:1．资源和环境约束下的共同物流体系面临很大风险，风险预测是共同物流运作风险管理的重要手段之一。2．传统的共同物流运作风险评估方法在准确性和客观性上存在难题，不能适应资源和环境约束下共同物流成员企业约束条件多、动态性强的特点。3．SVM方法与其他共同物流运作风险评价方法相比，在样本数量、运算准确率和运算速度等方面都显示了明显的优势。该方法完全可以应用于资源和环境约束下的共同物流运作风险预测这一复杂的领域中，进而为共同物流参与主体、行业主管部门及时做出合理的风险预防和控制措施提供科学依据。

［1］ 王理．制度变迁与我国资源型区域可持续发展［J］．河南大学学报 (社会科学版)，2007，(1)．

［2］ 欧阳小迅，黄福华．共同物流的构建机理与模式选择［J］．财经论从，2011，(11)．

［3］ 黄福华，周敏．基于共同物流视角的湖南农产品物流发展分析［J］．农业经济问题，2008，(8)．

［4］ 姜海燕，侯淑霞．物流基础设施对吸引物流业FDI影响的实证研究［J］．财经论从，2012，(1)．

［5］ 彭国樑，姚俭．不确定性供应链风险的模糊综合评判［J］．上海理工大学学报，2010，(4)．

［6］ Zhao Dongmei，Wang Changguang，Ma Jianfeng．A risk assessment method of the wireless network security ［J］．Journal of Electronics，2007，24(3)，pp．428 －432．

［7］ Goseva Popstojanova K．K．，Hassan A．Architectural level risk analysis using UML ［J］．IEEE Transactions Software Engineering，2003，29(10)pp．946－959．

［8］ Bedford T．，Cooke R．Probabilistic risk analysis［M］．Cambridge University Press，2001．

［9］ 韩敏，殷佳．一种用于小波网络隐层节点选择的新方法［J］．系统仿真学报，2007，(17)．

［10］ 蒋有凌，杨家其，尹靓，杨俊．基于ANN的供应链风险综合评估模型与应用［J］．武汉理工大学学报(交通科学与工程版)，2008，(1)．

［11］ 查健禄，田钦谟，李盛德．综合评价问题的系统分析［J］．系统工程学报，2000，(2)．

［12］ 姚建明，刘丽文．企业物流外包决策动因因素的结构关系分析［J］．商业经济与管理，2010，(10)．