Alpha稳定分布噪声下MPSK信号调制识别算法研究
2013-11-12赵春晖杨伟超
赵春晖,杨伟超
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
通信信号识别是软件无线电和认知无线电的关键技术,在军用电子对抗和民用频谱监测中也有广泛的应用.传统的通信信号识别算法通常将信道噪声建模为高斯噪声,事实上,这种假设在某些情况下是不准确的,因为在实际的通信信道中还时常出现一些尖峰状脉冲噪声,这些噪声往往幅值较大,不能忽略.近年来的研究发现,Alpha稳定分布是描述这种尖峰状脉冲噪声的最佳模型,越来越多的研究人员也开始将噪声建模为Alpha稳定分布[1-5].
通信信号的四次方谱是一种有效的分类特征,根据不同调制方式,信号具有不同的谱线特征,可以对某些信号实现有效识别[6-7].但是Alpha稳定分布噪声不具有α(α为特征指数)阶及以上各阶统计量,所以当背景噪声为Alpha稳定分布噪声时,通信信号的四次方谱就会失效.针对这个问题,本文提出了广义四次方谱的概念,并将其应用到MPSK 信号调制识别中,在Alpha稳定分布噪声下获得了较好的识别效果.
1 广义四次方谱
Alpha稳定分布是唯一满足广义中心极限定理的分布,是高斯分布的推广,即高斯噪声是Alpha稳定分布噪声的一个特例.Alpha稳定分布的一个最主要特征是其不具有α(0<α<2,α=2时即为高斯噪声)阶及以上各阶统计量[8].不失一般性,本文采用标准对称Alpha稳定(SαS)分布作为噪声模型.对于SαS 分布噪声来说,由于不存在有限的二阶矩,致使噪声的方差变得没有意义,因此采用混合信噪比[9]:

对于混有Alpha稳定分布噪声的接收信号,假设其模型为

式中,s表示接收信号;x 表示发送端信号;n 表示加性的Alpha稳定分布噪声.四次方谱定义为信号四次方的傅里叶变换,接收信号的四次方可表示为
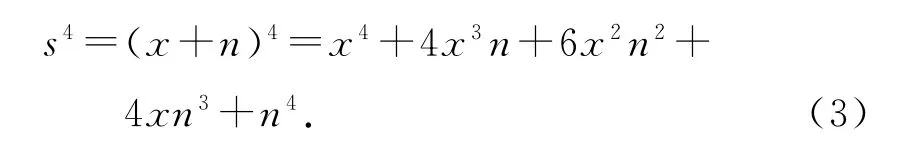
由式(3)可以看出,接收信号的四次方中含有6x2n2,4xn3和n4项,而由Alpha稳定分布噪声的性质可知,其不具有α 阶及以上各阶统计量,即6x2n2,4xn3,n4→∞,所以s4→∞.由傅里叶变换的约束条件可知,含有Alpha稳定分布噪声的接收信号的四次方谱不存在,或者说其四次方谱失效.图1给出了Alpha稳定分布噪声下(MSNR=15dB,α=1.5)BPSK 信号的四次方谱.由图1可以看出,由于噪声的影响,BPSK 信号的四次方谱被破坏.

图1 Alpha稳定分布噪声下BPSK信号的四次方谱Fig.1 Quartic spectrum of BPSK signal in the Alpha stable distribution noise
针对Alpha稳定分布噪声下信号四次方谱失效的问题,本文借鉴文献[10]的思想,提出了广义四次方谱的概念,定义如下:
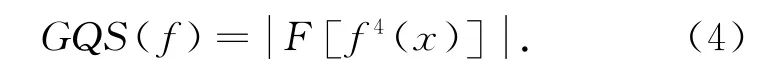
文献[10]通过推导说明了函数f(·)的主要作用是将含噪信号的幅值映射到一个有限区间,同时保持信号的相位不变,这样,接收信号的四次方就不再趋近于无穷大,可以对其进行傅里叶变换从而求得广义四次方谱.图2给出了和图1相同条件下的BPSK 信号的广义四次方谱.由图2可见,谱特性得到了极大的改善,可以将广义四次方谱作为Alpha稳定分布噪声下信号调制识别的分类特征.

图2 Alpha稳定分布噪声下BPSK信号的广义四次方谱Fig.2 Generalized quartic spectrum of BPSK signal in the Alpha stable distribution noise
2 特征提取与算法描述
本文选取MPSK 信号中使用较多且较难区分的BPSK,QPSK 和8PSK 信号作为待识别信号族.矩形脉冲成形的三种信号可以统一表示为
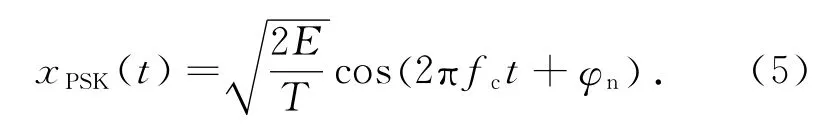
式中,E 表示信号能量;T 表示符号周期;fc表示载波频率;φn 表示受信息码元控制的相位参数,
由f(·)的性质可得

(1)对于BPSK 信号来说,φn∈{0,π},4φn∈{0,4π},2φn∈{0,2π},则

由式(8)可知,经过傅里叶变换后,BPSK 信号的广义四次方谱在零频率、±2fc和±4fc处会出现冲击谱线.
(2)对于QPSK信号来说,φn∈{0,π/2,π,3π/2},4φn∈{0,2π,4π,6π},2φn∈{0,π,2π,3π},则

式(9)第二项其实相当于载频为2fc的BPSK 信号,所以经过傅里叶变换,QPSK 信号的广义四次方谱在零频率和±4fc处有冲击谱线,另外还有中心位于±2fc处的sinc函数.
(3)对于8PSK 信号来说

式(10)第一项相当于载频为4fc的BPSK 信号,第二项相当于载频为2fc的QPSK 信号,则经过傅里叶变换,8PSK 信号的广义四次方谱除了有零频率处的冲击谱线外,还有中心分别位于±2fc和±4fc处的sinc函数.
图3给出了fc=0.15MHz的BPSK、QPSK和8PSK 信号的广义四次方谱图.由图3可以看出,三种信号的谱线特征和理论分析是相吻合的.
由图3及以上分析可知,三种信号的广义四次方谱中,二倍载频和四倍载频处的谱线特征是有效的分类特征,可利用其对三种信号进行分类识别.但是,如何区分冲击谱线和sinc函数是一个难点,本文定义了如下变量:


图3 MPSK信号的广义四次方谱图Fig.3 The generalized quartic spectra of the MPSK signals
因为谱线特征具有对称性,所以本文只取正半轴的谱线特征,即k1为对应于2fc的频率采样点,k1-1和k1+1为其相邻点;k2为对应于4fc的频率采样点,k2-1和k2+1为其相邻点.根据冲击谱线和sinc函数的性质可知,当2fc或4fc处为冲击谱线时,th1≫1,th2≫1;当2fc或4fc处为sinc函数的中心时,th1≈1,th2≈1.根据经验值,本文设定th1=th2=3 作为阈值来区分冲击谱线和sinc函数.
根据以上分析,算法简述如下:
(1)根据式(4)计算接收到信号的广义四次方谱;
(2)根据式(11)和式(12)分 别计算th1和th2;
(3)判断:当th1≥3时,判定为BPSK 信号;当th2≥3 时,判定为QPSK 信号;否则判定为8PSK 信号.
3 仿真实验与结果分析
为了验证算法的有效性,利用MATLAB 软件进行了相关的仿真实验.假设接收信号已经过预处理过程,即已估计出接收信号的载波频率,这部分不是本文的研究内容,不再赘述.实验中信号的载频fc=0.15MHz,采样频率fs=2.4MHz,码速率rs=24 000B/s,信号取8 192点.
实验1 验证基于广义四次方谱和四次方谱的识别算法在Alpha稳定分布噪声下的识别性能.采用本文提出的算法进行调制识别.因为信号的四次方和广义四次方有相同的相位,所以基于四次方谱的特征提取方法和基于广义四次方谱的特征提取方法相同.噪声为加性的标准SαS分布噪声,其中,取α=1.5.每种信号在每个混合信噪比下进行100次测试,正确识别的次数和总次数之比即为识别率.识别结果如图4所示.

图4 Alpha稳定分布噪声下的识别结果Fig.4 Recognition results in Alpha stable distribution noise
由图4可知,就基于广义四次方谱的算法而言,用于区分BPSK 信号和8PSK 信号的谱线特征比较明显,所以这两种信号在整个设定的混合信噪比范围内都有较高的识别率;QPSK 信号四倍载频处的冲击谱线幅值相对较小,容易受噪声的影响,所以信噪比较低时识别效果较差,当MSNR>10dB时,QPSK 信号的正确识别率大于80%.而基于四次方谱的算法中,BPSK 信号和QPSK 信号的识别率接近于零,算法失效,但是8PSK 信号的识别率较高.究其原因,主要是Alpha稳定分布噪声下四次方谱失效,导致其谱线出现如图1 所示的情况,这样,两个特征参数th1和th2都接近于1,致使算法将信号判断为8PSK 信号.从整体效果来看,仿真实验说明了Alpha稳定分布噪声下基于广义四次方谱的算法优于基于四次方谱的算法.
实验2 验证基于广义四次方谱和四次方谱的识别算法在高斯分布噪声下的性能.噪声为加性的高斯白噪声.每种信号在每个信噪比下进行100次测试,正确识别的次数和总次数之比即为识别率,实验结果如图5所示.

图5 高斯噪声下的识别结果Fig.5 Identification results in Gaussian noise
由图5可以看出,基于广义四次方谱和四次方谱的算法在所设定的信噪比范围内性能相当,当MSNR>8dB时,两种方法都可以对三种信号实现有效识别.说明基于广义四次方谱的算法在高斯分布噪声下也有良好的性能.
实验3 除了信噪比以外,Alpha稳定分布噪声的α 值也是影响算法性能的一个重要因素,本实验评估算法在不同α 值情况下的识别性能.噪声模型为加性的标准SαS分布,仿真当α 在区间[0.1,1.9]上以0.2为步长变化时,基于广义四次方谱的识别算法的性能.混合信噪比设定为15dB,每个α 值下进行100次测试,正确识别的次数和总次数之比即为识别率,实验结果如表1所示.

表1 不同α 值情况下的正确识别率Table 1 The correct recognition rate in the case of differentαvalues %
由表1可知,当特征指数α>1时,基于广义四次方谱的识别算法可以对BPSK 信号和QPSK信号实现有效识别,而8PSK 信号在整个α 区间都有较好的识别率,主要是因为α 值越小,Alpha稳定分布噪声的尖峰特性越明显,导致广义四次方谱二倍载频处和四倍载频处的谱线特征退化,所以对BPSK 信号和QPSK 信号影响较大,而对8PSK 信号几乎没有影响.实际通信信道中的尖峰脉冲噪声主要是α>1的Alpha 稳定分布噪声,α≤1的强尖峰脉冲噪声很少出现,所以本文所提算法适合在实际中应用.
从实验中可以看出,在Alpha稳定分布噪声下,虽然所提算法较基于四次方谱的算法性能有所提高,但是其运算过程中增加了广义化变换过程,其中涉及反正切和希尔伯特变换运算,致使算法的运算复杂度增加.
4 结 语
本文提出了一种基于广义四次方谱的MPSK 信号调制识别方法.利用信号广义四次方谱中二倍载频处和四倍载频处的谱线特征差异对所选信号进行识别.仿真结果表明,本文提出的算法在Alpha稳定分布噪声背景下和高斯噪声背景下都有较好的识别性能.算法的不足之处在于需要根据经验值来判定二倍载频处和四倍载频处的谱线是冲击谱线还是sinc函数,如何避开经验值,更智能地判别冲击谱线和sinc函数有待于进一步研究.
[1]Gu G D,Zhang Y S,Tian B.Estimation of LFM Signal's Time Parameters under the Alpha-stable Distribution Noise[C]∥Proceedings of IEEE Circuits and Systems International Conference on Testing and Diagnosis,Chengdu,2009:1-4.
[2]Rajan A,Tepedelenlioglu C.Diversity Combining over Rayleigh Fading Channels with Symmetric Alpha-stable Noise [J].IEEE Transctions on Wireless Communications,2010,9(9):2968-2976.
[3]Xia W J,Zhu L D,Xiong X Z.Fractional Lower Order Statistics based Generalized Constant Modulus Algorithm for Blind Multi-user Detection in DS/CDMA Systems[C]∥Proceedings of the International Conference on Wireless Communications and Signal Processing,Suzhou,2010:1-6.
[4]顾陈,何劲,朱晓华.冲击噪声背景下基于最小归一化均方误差的波束形成算法[J].电子学报,2010,38(6):1430-1433.(Gu Chen,He Jin,Zhu Xiaohua.Minimum Mean Square“Normalized-Error”Beamforming Amid Heavy-Tailed Impulsive Noise of Unknown Statistics [J].Acta Electronica Sinica,2010,38(6):1430-1433.)
[5]罗康生,赵明生.对称α 稳定分布噪声下的Turbo均衡[J].清华大学学报:自然科学版,2010,50(5):784-788.(Luo Kangsheng,Zhao Mingsheng.Turbo Equalization in Symmetricα-stable Noise Environments[J].Journal of Tsinghua University:Science and Technology,2010,50(5):784-788.)
[6]曾磊,陈铖,郭虹.卫星测控链路中PM,BPSK,QPSK 调制实时识别算法研究[J].现代电子技术,2009,32(17):59-62.(Zeng Lei,Chen Cheng,Guo Hong.Study of Real-time Modulation Recognition of PM,BPSK and QPSK Signals in TTC of Satellite Links [J].Modern Electronics Technique,2009,32(17):59-62.)
[7]吴月娴,葛临东,许志勇.常用数字调制信号识别的一种新方法[J].电子学报,2007,35(4):782-785.(Wu Yuexian,Ge Lindong,Xu Zhiyong.A Novel Identification Method for Commonly Used Digital Modulations[J].Acta Electronica Sinica,2007,35(4):782-785.)
[8]Jiang J L,Zha D F,Zhang Q.A Fast Algorithm of Logarithm-form Fractional Lower-order Spectrums[C]∥Proceedings of the Second International Conference on Computational Intelligence and Natural Computing,Wuhan,2010(1):29-32.)
[9]Guo W Q,Qiu T S,Tang H,et al.Performance of RBF Neural Networks for Array Processing in Impulsive Noise Environment[J].Digital Signal Processing,2008,18(2):168-178.
[10]赵春晖,杨伟超,马爽.基于广义二阶循环统计量的通信信号调制识别研究[J].通信学报,2011,32(1):144-150.)(Zhao Chunhui,Yang Weichao,Ma Shuang.Research on Communication Signal Modulation Recognition based on the Generalized Second-order Cyclic Statistic[J].Journal on Communications,2011,32(1):144-150.)
