目标函数带有阻塞率的输电阻塞成本控制优化模型及其求解

刘 斌，董秀娟，姜 囡，井元伟

（东北大学 信息科学与工程学院，辽宁 沈阳 110819）

随着电力市场的逐渐开放，输电网络阻塞问题变得日益严峻［1］.由于电力系统本身电力输送容量的限制，不能满足电能输送的要求，通常会发生输电线路或变压器的有功潮流超过允许极限，或是节点电压越限等情况［2］.同时，市场环境下的自由竞价及双边合同等因素也会增大不确定性，这些都需要合理地分摊风险成本，用正确的市场信号来引导利益不同的各市场方，达到降低风险的目的［3-5］.于是，设计损失最小的最优调整策略是必须要重视的问题.

针对经济负荷分配问题，文献［6］给出了一个优化问题的模型，并采用遗传算法给出了模型的解.针对超短期阻塞管理问题，文献［7］给出了在线管理模型和算法的设计.文献［8］则给出了一个相对简单的电力市场输电阻塞管理优化模型并设计了相应的阻塞费用计算规则.文献［9］提出了一种电力系统发电机调整费用最小的优化阻塞管理模型.文献［10］讨论了基于灵敏度分析的输电阻塞管理模型，给出了相应的算法.针对交流潮流模型，文献［11］提出了一种基于阻塞分布因子的区域电力市场阻塞管理问题的解决方法.

将潮流百分比即输电阻塞率作为目标函数或作为基本约束条件，是传统输电阻塞管理优化模型的特点之一［12］.传统的阻塞管理模型虽然能很好地反映电力系统的实际运行特征，但其求解从理论上来讲不是很容易的［13］.考虑单独开放发电侧的情况和同时开放发电侧与负荷侧的情况，本文分别讨论了阻塞管理的建模问题，建立了新的阻塞费用优化模型，让输电阻塞率参与到阻塞费用的计算当中.利用免疫遗传算法［14］对模型进行求解，得到了最优解.针对负荷分别为982.4和1 052.8MW的两个模型进行了仿真，结果表明所提出的改进阻塞费用模型与算法能更好地降低发电成本.

1 问题描述

假设一个电网内有s 条主要线路.一般情况下，将电网中每条线路上的有功潮流超过限值的百分比用来衡量输电阻塞的程度，亦即所谓的输电阻塞率，记为αk，具体计算公式为

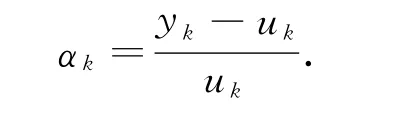
式中，k＝1，…，s为电网线路数，yk为线路k 上的有功潮流，uk为线路k的潮流限值，即安全裕度.输电阻塞率有时亦称为潮流比例系数.

当线路k 上的有功潮流小于安全裕度时，输电阻塞率αk＜0，电网处在正常运行状态；当有功潮流达到安全裕度时，αk＝0，电网处于提醒界限；而当线路上的有功潮流超出安全裕度时，αk＞0，此时电网已发生输电阻塞的情况，但还可以有效运行.当有功潮流持续增大，达到某一正数时，就会使系统瘫痪或崩溃，这一正数可称为极限裕度，记α＝maxαk，k＝1，…，s.

由于本文主要考虑输电阻塞发生时的情况，因此，可以认为总有αk＞0.

再假设此电网内有n 台发电机组，通过观察数据进行曲线拟合，各条线路上的有功潮流yk，k＝1，2，…，s与各机组出力xi，i＝1，2，…，n 之间的关系表达式如下

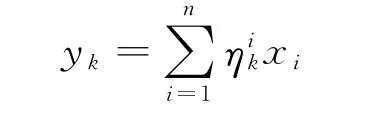
针对此类电网要考虑的问题是，如何调整调度方案，检查是否有阻塞发生，优化阻塞管理策略，使系统发电总成本最小.

2 基于输电阻塞率的阻塞管理模型

为了能更好地体现改进模型的特点和功能，本文将传统的输电阻塞控制模型作以简单介绍.

2.1 传统输电阻塞控制模型

这里只介绍如下的两个模型.

（1）基于节点电价法的阻塞控制模型.节点电价模型实质上是一个基于集中调度的最优潮流（Optimal Power Flow，OPF）问题［10］.

根据电力市场开放程度不同，OPF 模型的目标函数包括发电侧开放和用户侧亦开放两种.前者的OPF目标函数为系统总发电成本最小，即

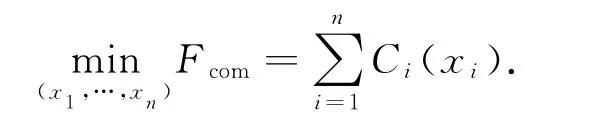
式中，Ci（xi）为发电机组i的发电成本报价，Fcom为系统发电总成本.

而后者的OPF目标函数为社会效益最大（或社会成本最小），即

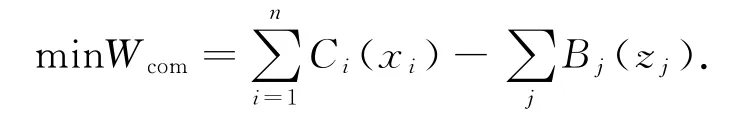
式中，zj为用户j的负荷功率，Bj（zj）为用户j的效用函数，Wcom为社会成本.

（2）发电侧费用最小模型.此类模型的目标函数为

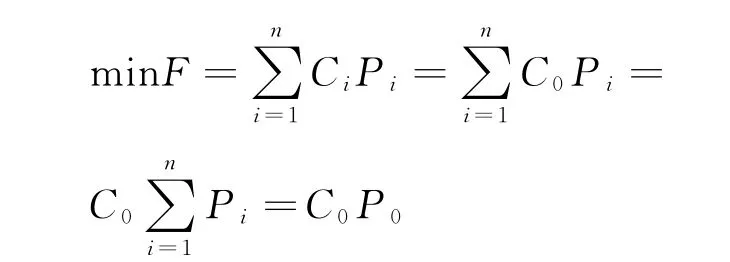
式中，各变量及参数的含义参见文献［15］.该模型是以网方的购电费用最小为目标函数的，并没有考虑线路的安全等情况，而在约束条件当中体现的也多是硬件上的约束.约束条件如下：

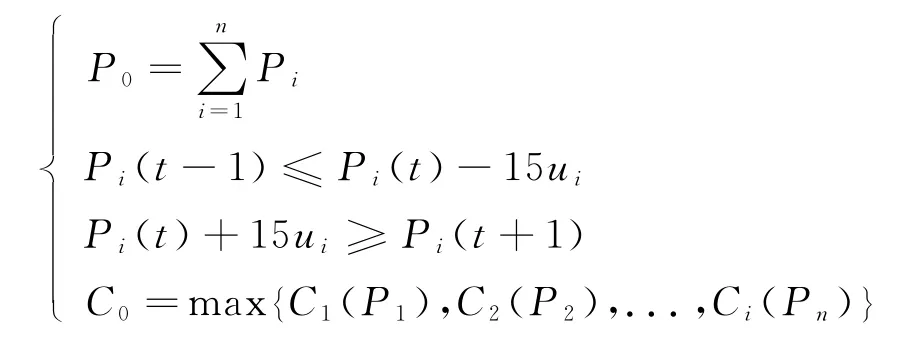
式中，Pi为机组i的预出力，Ci为机组i 出力Pi时的报价，P0为负荷需求量，ui为机组i的爬坡速率.

以上模型以传统的方式只考虑了发电侧的阻塞费用，而没有体现用户侧存在可中断负荷的情况.那么当用户侧可中断负荷存在时，模型就需要进行改进以适应这种情况.

2.2 改进的输电阻塞控制模型

仅将潮流越限作为约束条件或者作为目标函数之一时，并不能完全体现潮流对阻塞费用的影响.为此将输电阻塞率α 引入费用模型的目标函数当中.当潮流阻塞不可避免时，输电阻塞率越大，相应的阻塞费用则越多.

（1）发电侧单独开放.这时只需在发电侧进行调整，目标函数为发电机调整费用最小，同时将输电阻塞率α 作为影响目标求极小的反向因素加入目标函数中.在输电阻塞率α 对目标影响最大的情况下求取最佳出力调整方案，使系统的目标成本值最小.模型具体形式为

式中，xi为机组i 在下一时段分配预案中的出力，Pi为机组i出力xi所在段对应的段价，λi为机组i在发生阻塞后的出力改变量，B为下一时段预报的负荷要求，Ci为机组i 当前出力，T为一个时段的时间长度，dij为机组i 在线路j的容量，eij为如下形式的二值函数：

第1个条件和第2个条件是为确保预测负荷满足需求.即，当负荷需求为B 时，各发电机组出力总量不论在调节前还是在调节后都应该正好满足负荷需求.第3个条件表示，如果在预案中当前预测的出力为Ci，那么下一时段的出力的调整分配量xi就会落在与机组爬坡速率相关的区间［Ci-Tui，Ci＋Tui］内.第4个条件约束了机组的出力容量，即机组的出力不能大于该机组在各线路的出力之和.

在模型的目标函数中引入反向作用的量，这就使得问题转化为一类极小极大问题.这类问题考虑了最不理想（或最坏）情况，从而适用范围更广，得到的结果更具普遍性.

（2）负荷侧与发电侧同时开放.对于此类模型，要考虑由于负荷中断所造成的相应补偿问题.假设Qj为补偿价格，γj为调整的中断负荷，那么γjQj就表示了因负荷中断需要补偿的费用.类似于单独开放发电侧的情况，结合输电阻塞率α 对阻塞费用的影响，以调整费用最小为目标建立如下的优化模型.

式中，l为参与可中断负荷管理并在辅助服务市场竞标成功的用户个数，其他符号意义同前.

当输电阻塞率增大时，出力的调整量λi也相应增加，调整费用的成本就会上升，而本文的最终目标是降低阻塞费用，因此这是个典型的对策问题，在下一节将针对所建立的模型进行求解，以验证模型的安全可靠性.

3 基于免疫遗传算法的模型求解

免疫遗传算法可用来求解这类优化问题，但它又有收敛方向无法控制的缺陷.为此将目的函数和制约条件作为抗原，就能够保证所生成的抗体直接与问题相关联，收敛方向能得以控制.所生成的抗体能有效地排除无用抗原，这就等价于求得了问题的最优解.将与抗原亲和力高的抗体进行记忆，可促进快速求解，即当遇到同类抗原时，可以快速生成与之对应的抗体.

免疫遗传算法中，初始解是算法的起点.在输电阻塞模型中，若确定了各机组重新分配预案的出力矩阵中各元素的解区间和其他相应的约束条件，就可以给出满足约束条件的解作为初始解.

设各机组重新分配预案的出力矩阵为X＝［x1，x2，…，xn］，这是一个s×n 矩阵.在具体求解的过程当中，先根据已知数据和不等式约束条件，将机组i的出力约束在［ai，bi］内.并将第n台机组的出力用其他机组的出力表示，以满足等式条件约束，即：

结合免疫遗传算法的具体流程，对输电阻塞模型求解的算法框架可以描述如下：

（1）编码（机组排列）.对于输电阻塞问题，抗体就是对应满足约束条件的可行解.采用二进制符号串来表示群体中的个体，满足各机组的约束条件，取8位2进制表示一台机组，n 台机组即8n 位2进制码.

（2）选取初始种群.对于初次应答，初始种群随机产生，而对于再次应答，则借助免疫机制的记忆功能，部分初始抗体可从记忆单元当中获取.这里初始群体随机产生符合约束条件的n 台机组出力.

（3）计算适应度和抗体浓度.将目标函数取作适应度函数，通过计算抗体间的亲和度，进而计算抗体的浓度.

（4）概率选择策略.为了保证抗体的多样性，并且保证优秀抗体能够进入下一代，采用基于抗体浓度和适应度的概率选择策略，增加算法的搜索空间，将优秀抗体更好地保存和繁殖.

（5）遗传操作.在交叉过程的开始，先从（0，1）范围内产生一个随机数Rk，并与交叉概率Pc进行比较，若有Rk＜Pc，则进行交叉运算.否则不进行交叉操作.变异过程首先按如下公式确定每个抗体进行变异的位数.式中，bit是要进行变异的位数，f 是要进行变异操作的抗体的亲合度，fmax和fmin分别是整个群体的最高亲合度和最低亲合度，μ 和ν 是预先设定的最大和最小的变异位数.

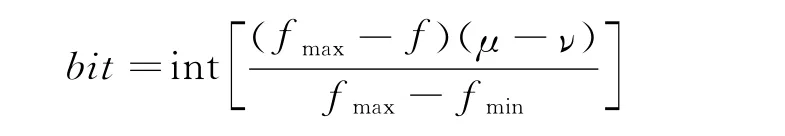
（6）免疫操作.对种群进行概率Pm的免疫操作.

（7）终止.条件判断，输出寻优结果，在此终止条件为算法规定最大迭代次数.

4 仿真分析

在仿真中假设有n＝8，s＝6，那么机组8的出力用其他机组的出力来表示，则有

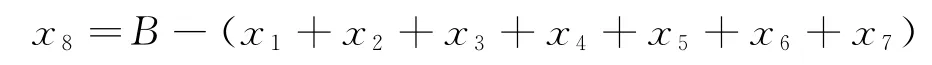
根据多次试验，选择Pc＝0.8，Pm＝0.001，取迭代200次基本上就会达到较好效果，同时由于阈值太大或太小都会减慢收敛速度，因此选浓度阈值η＝0.6.

算例1 负荷需求为982.4MW

考虑负荷需求预测B＝982.4MW 情况下的仿真问题.表1给出了当前机组的出力值以及爬坡速率.表2则给出了各机组出力及对应的报价情况.

表2给出的预案是根据电力市场的交易规则而确定的，此为出力预案不变时机组的数据.那么有

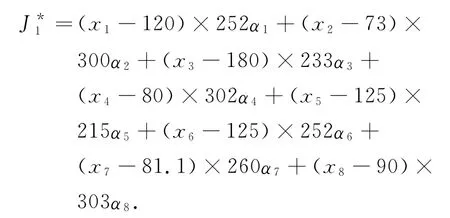
取αk为0.02，可得到由于负荷需求增加而需要支付的原始费用为597.694元.

表1 各机组当前出力及爬坡速率Table 1 The present output and climb rate of generators

表2 各机组分配预案Table 2 Thepre-distribution scheme of each generator

首先是初始化群体，经过MATLAB 运算得到阻塞费用随迭代次数而变化的仿真曲线，如图1所示.

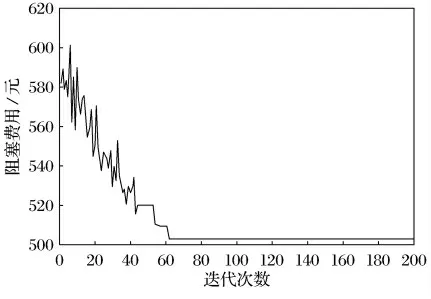
图1 负荷需求为982.4MW 时的费用成本曲线Fig.1 The adjustment cost when load is 982.4MW

求解得到调整出力后的最小费用为502.64元.对应的可节约费用为95.004元.各机组出力结果如下：

算例2 负荷需求为1 052.8MW

考虑负荷需求预测B＝1 052.84MW 情况下的仿真问题.表3 是当负荷需求为1 052.8MW时的预出力分配方案.

取αk为0.07，可得由于负荷需求增加而需要支付的原始费用为3 845.814元.

首先设最大循环次数t＝200，种群个体个数M＝8，适应度比较时的N＝6，交叉概率Pc＝0.8，变异概率Pm＝0.001，时段长度Ti＝15，浓度阈值η＝0.6.取迭代次数为算法终止条件.

表3 对应机组预出力Table 3 The generator forecasting output

经过MATLAB运算得到阻塞费用随迭代次数而变化的仿真曲线，如图2所示.

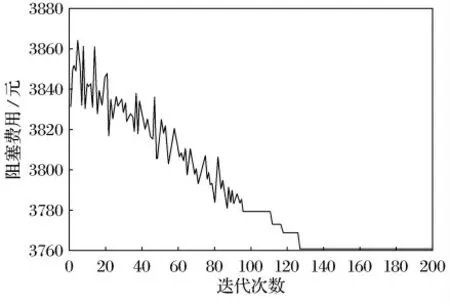
图2 负荷需求为1 052.8MW 时的费用成本曲线Fig.2 The adjustment cost when load is 1 052.8MW

可得调整出力后的最小费用为3 758.7 元，对应初始预案的可节约费用为107.114元.优化后的各机组出力如下：

从图1和图2中可以明显看出，当负荷需求增大时，对应的发电成本费用也相应的增加.因此本文在此时考虑采用可中断负荷来实现高负荷需求时的费用管理.

基于表3给出的相同的预出力的分配方案，且同样考虑负荷需求为1 052.8MW，同文献［8］和文献［16］做以比较.文献［8］建立了双目标规划模型，并将阻塞率因子作为目标函数之一，文献［16］将阻塞率因子引入目标函数中，两者都是应用模拟退火算法调整机组出力，求得的阻塞费用为6 640.8元和3 780.9元.通过和图2中的结果相比较，可见本文将阻塞率因子直接引入输电阻塞管理优化模型中并应用免疫遗传算法求得的需要支付的调整费用3 758.7元，因此，本文的优化方案确实可以更加节省调整成本.

算例3 可中断负荷模型

现在假设当前出力不变仍为表1所示，负荷需求为1 052.8MW.此时根据可中断协议，用户端存在可中断负荷，且中断量为30.4MW.由于实行了中断负荷，各机组出力按中断后剩余的负荷需求实行出力预案的分配，那么此时对应的αk最大值为0.02.经过运算可得由于中断所需要支付的费用为

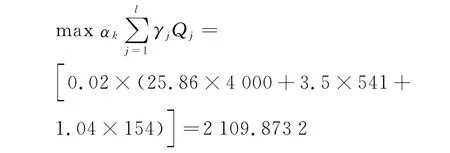
经过MATLAB 仿真得到费用成本曲线如图3所示.

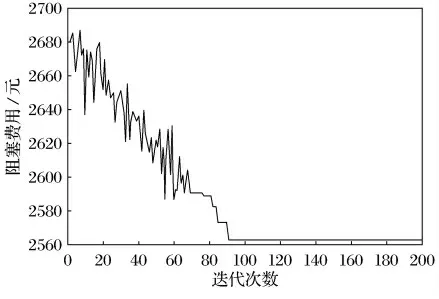
图3 存在可中断负荷时的费用成本Fig.3 The adjustment cost when existing the interruptable load

经计算得到发电成本为2 562.8 元，与未采用可中断负荷模型时得到的发电成本费用3 780.9元相比，发电成本费用有大幅度的削减.此时机组出力为

由此可见，合理地签订用户中断协议可以显著削减阻塞费用，提高社会效益.

5 结 论

本文针对发电侧单独开放以及负荷侧与发电侧同时开放两种情形，讨论了输电阻塞成本管理问题.改进了阻塞费用优化模型，实现了将潮流越限的情况进行责任化，同时可以简化求解过程.利用免疫遗传算法对负荷分别为982.4MW和1 052.8MW 时的模型进行了算法设计和仿真验证，结果表明所提模型可以显著降低发电成本.由于随着负荷需求增加，阻塞费用也相应增多，进而采用可中断负荷模型，有效地缩减和控制了调整费用.

［1］张永平，焦连伟，陈寿孙，等.电力市场阻塞管理综述［J］.电网技术，2003，27（8）：1-9.（Zhang Yongping，Jiao Lianwei，Chen Shousun，et al.A Survey of Transmission Congestion Management in Electricity Markets［J］.Power System Technology，2003，27（8）：1-9.）

［2］Christle R D，Wollenberg B F，Wangensteen.Transmission Management in the Deregulated Environment［J］.IEEE Trans on Power System，2000，15（2）：171-195.

［3］Shrestha G B，Fonseka P A.Congestion-driven Transmission Expansion in Competitive Power Markets［J］.IEEE Transaction on Power System，2004，19（3）：1-8.

［4］Mendez R，Rudnick H.Congestion Management and Transmission Rights in Centralized Electric Markets［J］.IEEE Transaction on Power System，2003，19（2）：889-896.

［5］王丹，李彦平.基于激励策略自报电量的电价算法研究［J］.沈阳大学学报：自然科学版，2012，24（1）：20-24.（Wang Dan，Li Yanping.Power Pricing Algorithm of Consumption Report Model based on Incentive Strategy［J］.Journal of Shenyang University：Natural Science，2012，24（1）：20-24.）

［6］何大阔，王福利，贾明兴，等.遗传算法在电力系统经济负荷分配中的应用［J］.东北大学学报：自然科学版，2006，27（11）：230-233.（He Dakuo，Wang Fuli，Jia Mingxing，et al.Application of Genetic Algorithm in Economic Dispatch of Power Systems［J］.Journal of Northeastern University：Natural Science，2006，27（11）：230-233.）

［7］吴政球，朱民茂，王良缘，等.超短期在线输电阻塞管理模型及算法［J］.电力系统及其自动化学报，2007，19（6）：109-113.（Wu Zhengqiu，Zhu Minmao，Wang Liangyuan，et al.Online Transmission Congestion Management Model and Algorithm［J］.Journal of Electric Power System and Automation，2007，19（6）：109-113.）

［8］易兆麟.电力市场的输电阻塞管理的优化模型［J］.衡阳师范学院学报，2006，27（3）：22-25.（Yi Zhaolin.The Optimize Model on Management of Transmit Electricity Block in the Electric Power Market［J］.Journal of Hengyang Normal University，2006，27（3）：22-25.）

［9］Lei J，Deng Y，Zhang R.Congestion Management for Generation Scheduling in a Deregulated Chinese Power System［C］.IEEE Society Winter Meeting on Power Engineering，2001，3：1262-1265.

［10］王秀丽，甘志，雷兵，等.输电阻塞管理的灵敏度分析模型及算法［J］.电力系统自动化，2002，26（4）：10-13.（Wang Xiuli，Gan Zhi，Lei Bing，et al.Sensitivity Analysis Approach to Transmission Congestion Management［J］.Automation of Electric Power Systems，2002，26（4）：10-13.）

［11］Kumar A，Sristava S C，Singh S N.Anovel Congestion Management Approach Using AC Transmission Congestion Distribute Factor［J］.Electric Power Systems，2004，72（1）：85-93.

［12］孙勇智，韦巍.基于人工免疫算法的电力系统最优潮流计算［J］.电力系统自动化，2002，26（12）：30-34.（Sun Yongzhi，Wei Wei.Solution of Optimal Power Flow Problem Based on Artificial Immune Algorithm ［J］.Automation of Electric Power Systems，2002，26（12）：30-34.）

［13］毛伟明，周明，李庚银.多时段下计及可中断负荷的电网输电阻塞管理［J］.电网技术，2008，32（4）：72-77.（Mao Weiming，Zhou Ming，Li Gengyin.Multi-period Power Transmission Congestion Management Considering Interruptible Loads［J］.Power System Technology，2008，32（4）：72-77.）

［14］李茂军.人工免疫算法及其应用研究［J］.控制理论与应用，2004，2l（2）：153-157.（Li Maojun.Artificial Immune Algorithm and its Applications ［J］.Journal of Control Theory and Applications，2004，21（2）：153-157.）

［15］Singh H，Hao S，Papalexopoulos A D.Transmission Congestion Management in Competitive Electricity Markets［J］.IEEE Transactions on Power Systems，1998，13（2）：672-680.

［16］刘斌，姜囡，井元伟.基于模拟退火算法的电力系统输电阻塞成本控制［J］.控制与决策，2010，25（8）：1184-1188.（Lin Bin，Jiang Nan，Jing Yuanwei.Cost Control of Transmission Congestion Management in Electricity Systems based on Simulated Annealing Algorithm［J］.Journal of Control and Decision，2010，25（8）：1184-1188.）