非线性不确定时变时滞中立系统的非脆弱控制
2013-11-12胡何丽
胡 何 丽
(沈阳大学 装备制造综合自动化重点实验室,辽宁 沈阳 110044)
现实系统中广泛地存在着滞后现象.无论是工程技术领域,还是物理学、化学、生物医学等领域,基于实际问题提出的数学模型都含有典型的滞后信息.尤其是带有反馈的自动控制系统装置,在系统的控制输入信号和收到系统的反馈信号之间,显然有一个时间延迟,即时滞.因此,采用传统的微分方程来描述系统,得到的只能是系统状态的一种近似行为,并且如果达不到系统的性能的要求,则会出现错误、故障,甚至使得系统崩溃.特别是,由于系统元器件的老化和现场恶劣的环境等诸多因素的影响,可能使得系统控制器参数的微小变化导致系统性能的下降甚至使得控制器起不到作用,完全失效[1-3].因此,人们对实际工程控制系统提出更高的要求,不但要求系统的模型相当准确的描述系统的行为,而且要求系统的控制器能较快并允许一定的摄动来实现系统的稳定等性能.于是,考虑系统带有不确定项,并且考虑控制器参数具有摄动情况的这类实际系统,得到了广大学者的广泛关注.文献[4]提出一种混合LQ/H∞非脆弱模糊控制器的设计方法,研究当控制器存在可加性摄动时仍能保持对系统的镇定并满足给定的LQ/H∞性能指标.文献[5]针对变机翼后掠角NSV 设计了多模型软切换保性能非脆弱控制方案,根据可测前提变量将系统工作空间利用划分为多个子区域,并将各局部控制器在模糊子区域的的边界上进行切换,系统的控制器由各局部控制器按照模糊加权得到.
中立系统是一类特殊的时滞系统,其主要特征是:系统中既含有状态变量的最高阶导数,还含有带有时滞的状态变量的最高阶导数[6].实际工程系统中广泛存在着这样的中立型微分方程,例如化工过程的双级溶解槽、人口免疫反应、薄的运动体的连续热感应、全波等效电路、无损电线传输等.文献[7]提供了一个用来描述无损电线传输中,电压和电源的波动模型四维线性中立型时滞系统.另外,中立型时滞系统亦出现在涡轮喷气式飞机引擎系统,人口动态以及血液中的白蛋白分布等问题的研究中.因此,近年来中立型时滞系统的理论研究备受研究者的青睐[8-19].Quan等人[8]研究了在一类临界情况下即:中立项系数矩阵的谱半径等于1时的线性中立系统的稳定性问题,得到的稳定性判据符合当系统的中立项系数矩阵具有Jordan块时系统不稳定的事实.在文献[9]中,Moezzi和Aghdam 考虑了具有不确定项的时滞中立系统的自适应鲁棒镇定问题,提出(4一)个新颖的无记忆自适应状态反馈控制器,同时引入一个自适应策略用于估计系统不确定项的界.Wang[10]等人开发了一种代数矩阵方程方法来有效处理全阶观测器设计问题,确保误差动态系统指数稳定.然而,由于中立系统自身的复杂性,关于中立系统的非脆弱控制研究的文献却较少.
本文考虑系统状态、控制输入均含有时变时滞的非线性不确定中立系统在控制器存在摄动的情况下系统的鲁棒控制问题.考虑的系统的非线性扰动仅可知其幅值界,同时采用灵活的矩阵分解和放大技巧,并引入一个积分不等式用于放大因求取Lyapunov泛函的导数产生的积分项,得到保证系统渐近稳定的基于线性矩阵不等式的稳定判据.另外,给出保证系统渐近稳定的对含有不确定的中立项系数的约束条件.通过数值例子和仿真结果展现本文结果有效性.
1 问题描述
考虑如下一类非线性不确定中立系统:

式中,x(t)∈Rn和u(t)∈Rm分别为系统的状态和控制输入向量;A,Aσ,Aη,B 和Bδ为已知的适当维数的矩阵;φ(t)是系统的初始条件;σ(t),η(t)和δ(t)表示时变时滞.
假定存在满足如下约束条件的常数f0,g0,h0,f,g,h 和l:
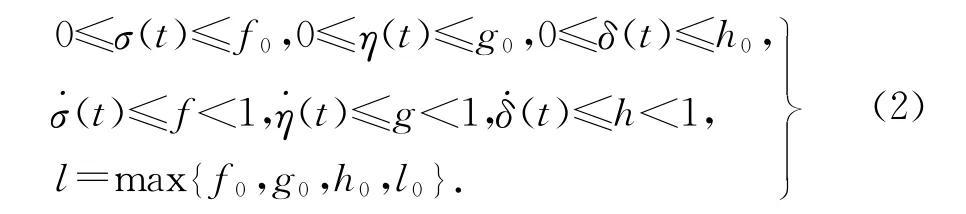
时变参数不确定项ΔA(t),ΔAσ(t),ΔAη(t),ΔB(t),ΔBδ(t)具有如下形式:
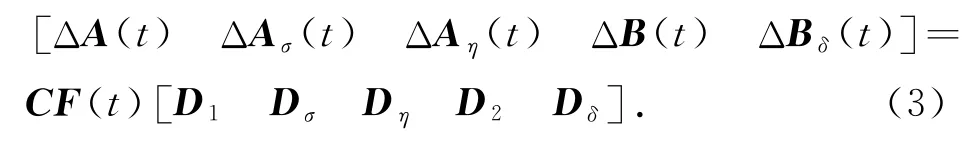
式中,C,D1,Dσ,Dη,D2和Dδ是适当维数的常数矩阵;F(t)为满足如下约束的未知矩阵:
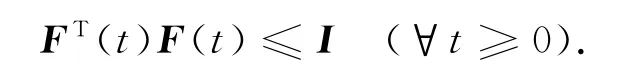
假定时变非线 性扰动ω(t,x(t),x(t-τ(t)))幅值有界,满足
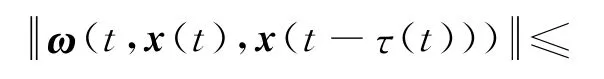

构造如下状态反馈控制器:

式中,K∈Rm×n是要设计的控制器增益,并且ΔK是控制器增益扰动,ΔK=M¯F(t)N,M 和N 是适当维数的常数矩阵,¯F(t)为满足如下约束的未知矩阵:

本文的目标是对在具有约束(2)、(3)、(4)下的系统(1),设计形如(5)的控制器,使得闭环系统渐近稳定.若这样的控制器存在,则控制器(5)是考虑系统的非脆弱控制器.
引理1 对于任意的矩阵P>0和适当维数的可微向量x(t),有
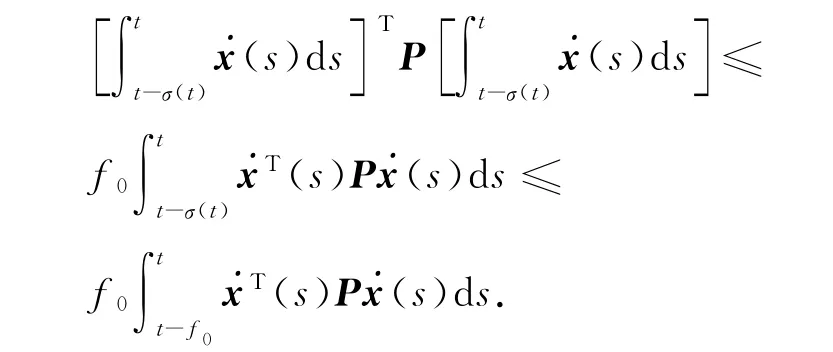
引理2 假定Z、X、S 和Y 是适当维数的矩阵,且Z 是对称矩阵,STS≤I,那么Z+XSY+YTSTXT<0成立当且仅当存在ε>0,满足如下不等式:

2 主要结果
定理 在具有约束(2)、(3)、(4)下的系统(1)是渐近稳定的,如果存在正数ε1、ε2、ε3、ε4,对称正定矩阵Q0、Q1、Q2、Q3和矩阵X,使得如下线性矩阵不等式(LMI)成立:

那么控制器(5)是系统(1)的非脆弱控制器.其中,控制器增益K的表达式为K=,并且
与廖仲结婚前,买房时,我选择了大家公认的完美方案:买在公公婆婆居住的小区,中间隔着6栋房子,看不到彼此,但能以最快的速度出现在彼此家中。我心想,这样一来,以后蹭饭、照顾孩子、照应老人都方便。



显然,对于所有的x(t)≠0,有V(x(t),t)>0.对V(x(t),t)的导数应用约束(2)、(3)、(4)和引理1,并经过简单推导,易得

式中

对式(10)左乘YT,右乘Y,其中
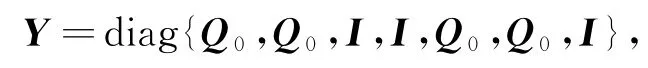
得到

式中,


式中,

对矩阵进行分解,得到如下表达式:
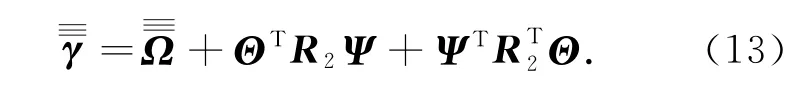


依据引理2 和Schur Complement公式,不等式(6)Γ<0 等价于式(13<0.而对式(13)应用引理2 和Schur Complement公式,得到<0.条件<0 意味着<0.再一次对<0应用Schur Complement公式,得到γ<0.因此,存在常数ρ>0,使得如下不等式成立:
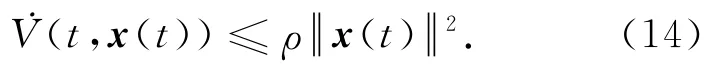
对不等式(7)应用Schur Complement公式并采用矩阵的分解技巧,易知不等式(7)等价于

因此,若LMIs(6)和(7)成立,则不确定非线性中立系统(1)是渐近稳定的.
3 仿真例子
考虑非线性不确定系统(1),系统的参数如下:

求解LMIs(6)和(7),得到如下计算结果:


进一步地,系统的控制器增益为
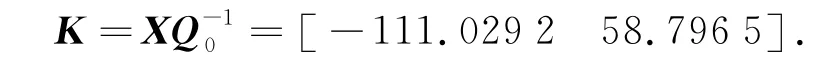
当系统的初始条件和未知矩阵F(t),¯F(t)分别如下取值
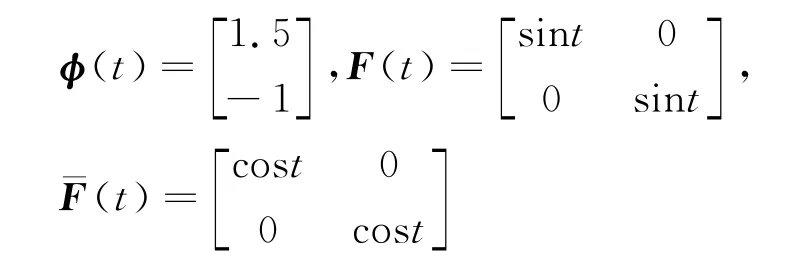
时,对系统(1)采用如上数据进行仿真,仿真结果如图1和如图2所示.

图1 开环系统的状态曲线Fig.1 State curve of the open loop system
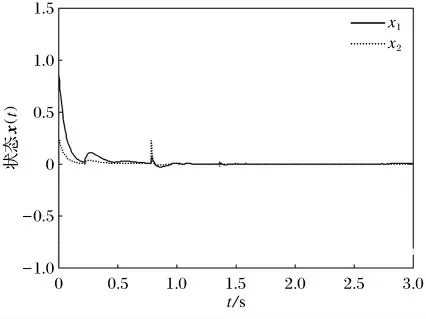
图2 闭环系统的状态曲线Fig.2 The state of the closed-loop system curve
从图1可以看出,不含有控制器的开环系统(1)是发散的;施加了控制器(5)后,系统(1)迅速收敛,在1s时几乎达到了很好的收敛效果(图2).
4 结 语
研究带有时变时滞的非线性中立系统的鲁棒控制问题相当复杂,具有一定的挑战性.本文在Lyapunov稳定性理论框架下,设计具有加性扰动的控制器,采用灵活的矩阵分解和放大技巧,并引入一个积分不等式,推导出确保考虑的系统具有渐近稳定性的判据.通过求解LMI,可以方便地得到系统的状态反馈控制器增益矩阵.数值例子和仿真结果进一步验证了所设计非脆弱控制方法的有效性.
[1]Yang G H,Che W W.Non-fragile H∞Filter Design for Linear Continuous-time Systems[J].Automatica,2008,44(11):2849-2856.
[2]Keel L H,Bhattacharyya S P.Robust,Fragile,or Optimal[J].IEEE Transactions on Automatic Control,1997,42(8):1098-1105.
[3]王丹,李彦平,郝彬彬.基于随机交叉机制的同步优化网络模型[J].沈阳大学学报:自然科学版,2012,24(3):43-46.(Wang Dan,Li Yanping,Hao Binbin.Synchronizationoptimal Network Model based on Random Interchanging Mechanism[J].Journal of Shenyang University:Natural Science,2012,24(3):43-46.)
[4]陈珺,刘飞.离散模糊时滞系统的鲁棒LQ/H∞非脆弱控制[J].系统工程与电子技术,2010,32(1):126-132.(Chen Jun,Liu Fei.Robust LQ/H∞Non-fragile Control for Discrete-time Fuzzy Systems with Time Delay[J].Journal of Systems Engineering and Electronics,2010,32(1):126-132.)
[5]王宇飞,姜长生,吴庆宪.近空间飞行器多模型软切换保性能非脆弱控制[J].控制理论与应用,2012,29(4):440-446.(Wang Yufei,Jiang Changsheng,Wu Qingxian.Multimodel Soft-switching Cost-guaranteed Non-fragile Control for Near-space Vehicle [J].Control Theory &Applications,2012,29(4):440-446.)
[6]Kolmanovskii V B,Richard J P,Tchangani A P.Stability of Linear Systems with Discrete-plus-distributed Delays:Application to Some Model Transformations[C]∥Proceedings of MTNS.Padova,1998.
[7]Salamon D.Control and Observation of Neutral Systems[M].Boston:Pitman Advanced Publishing Program,1984.
[8]Quan Q,Yang D,Cai K.Linear Matrix Inequality Approach for Stability Analysis of Linear Neutral Systems in a Critical Case[J].IET Control Theory and Applications,2010,4(7):1290-1297.
[9]Moezzi K,Aghdam A.Adaptive Robust Control of Uncertain Neutral Time-delay Systems [C]∥2008 American Control Conference.Seattle,2008.
[10]Wang Z,Lam J,Burnham K.Stability Analysis and Observer Design for Neutral Delay Systems[J].IEEE Transactions on Automatic Control,2002,47(3):478-483.
[11]Xu S,Chu Y,Lu J W,et al.Exponential Dynamic Output Feedback Controller Design for Stochastic Neutral Systems with Distributed Delays[J].IEEE Transactions on Systems,Man,and Cybernetics:Part A:Systems and Human,2006,36(3):540-548.
[12]Baser U,Kizilsac B.Dynamic Output Feedback H∞Control Problem for Linear Neutral Systems[J].IEEE Transactions on Automatic Control,2007,52(6):1113-1118.
[13]Darouach M.Reduced-order Observer for Linear Neutral Systems[J].IEEE Transactions on Automatic Control,2005,50(9):1407-1413.
[14]Mahmoud M S.Robust H∞Control of Linear Neutral Systems[J].Automatica,2000,36(5):757-764.
[15]苏春华,刘思峰.一类区间随机分布时滞系统的p-阶矩指数稳定性[J].应用数学,2009,22(2):413-420.(Su Chunhua,Liu Sifeng.p-Moment Exponential Stability for a Class of Interval Stochastic Distributed Delay Systems[J].Mathematica Applicata,2009,22(2):413-420.)
[16]Park J H,Choi K.Guaranteed Cost Control of Uncertain Nonlinear Neutral Systems via Memory State Feedback[J].Chaos Solitons and Fractals,2005,24(1):183-190.
[17]Sun X,Zhao J.Robust Adaptive Control for a Class of Nonlinear Uncertain Neutral Delay Systems[C]∥Proceeding of the 2004 American Control Conference.Boston,2004.
[18]Rodriguez S,Dugard L,Dion J,et al.On Delaydependent Robust Stability under Model Transformation of Some Uncertain Neutral Systems[J].Kybernetika,2009,45(5):825-840.
[19]Fridman E.New Lyapunov-Krasovskii Functionals for Stability of Linear Retarded and Neutral Type Systems[J].Systems &Control Letters,2001,43(4):309-319.
