HHT算法在电力系统谐波分析中的应用研究

程 琼 ，陈明德

(湖北工业大学电气与电子工程学院， 湖北 武汉 430068)

谐波检测的关键在于准确检测出谐波的频率、幅值等属性．但由于电力系统谐波具有固有非线性、随机性、分布性、非平稳性和影响因素的复杂性等特征，给谐波的检测带来极大困难．常用的谐波分析方法主要有[1-3]：模拟滤波器法、瞬时无功功率法、傅里叶变换以及小波变换等．模拟滤波器法对电路元件参数要求较高，实时性差，精度也比较低；瞬时无功功率法的检测结果误差大，对于单相电路的检测算法复杂，不易实现；基于傅里叶变换及其改进的方法存在一定的频谱泄漏和栅栏效应，且对暂态信号难以检测；基于小波变换的检测法只对低频段进行分解，造成高频段分辨率较低，降低了高次谐波的检测精度．因此，研究一种能在非线性、非平稳的电力系统谐波信号中准确提取谐波参数的方法十分重要．文献[4]提出了Hilbert-Huang (Hilbert-Huang Transform,HHT)变换；文献[5]将HHT应用于电力系统的电能质量检测中．HHT具有不受非稳态信号限制、多分辨率等优点，近年来在各领域中的应用研究越来越多[6-8]．

本文概述了HHT的基本理论，进而将其应用于电力谐波分析中．通过EMD(Empirical Mode Decomposition)分解，实现各次谐波的提取和区分．通过Hilbert变换得到各次谐波的瞬时幅值和瞬时频率，并能准确得到谐波信号突变的时刻．

1 基于HHT算法的谐波分析原理

1.1 HHT的基本原理

HHT变换是一种具有一定自适应的信号分析方法，首先采用EMD算法将复杂信号x(t)分解为若干个IMF(Intrinsic Mode Function)分量之和[9-11]，即

(1)

式(1)中i表示经过EMD分解后得到的IMF模态的顺序编号．对信号x(t),定义它的Hilbert变换为

τ.

(2)

经过反变换，得解析信号z(t)=x(t)+jy(t)．由解析信号，可求出信号对应的瞬时幅值a(t)、瞬时相位φ(t)和瞬时频率f(t)，即

(3)

(4)

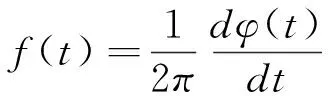
(5)

HHT算法流程图见图1．

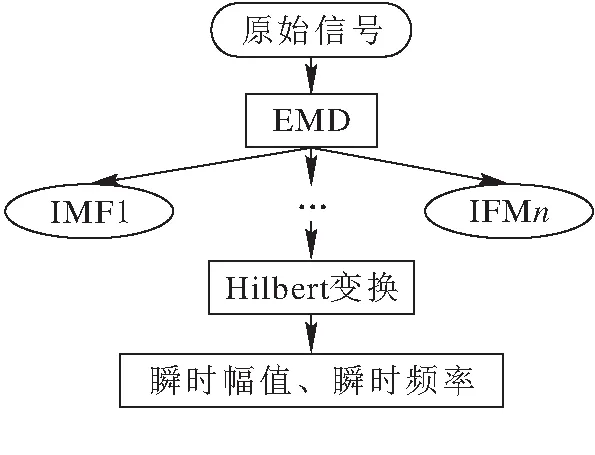
图 1 HHT算法流程图

1.2 基于HHT的谐波分析方法

电力系统中的电压和电流谐波信号可以表示为

π×fnt+αn),

(6)

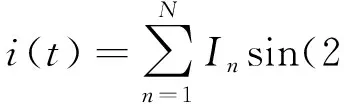
(7)

式(6)、(7)中：Un、In表示第n次谐波电压和电流的幅值；αn、βn表示谐波相位；n表示谐波次数；N表示谐波最高次数；fn表示第n次谐波频率[12-13]．

将电压信号进行EMD分解，即可得

(8)

同理，根据式(3)(4)(5)即可依次得电压、电流信号中各次谐波的瞬时幅值、相位和频率．

2 谐波检测算法的仿真分析

2.1 稳谐波信号的分析

对于平稳谐波信号，设仿真信号x(t)=sin(2π×50t)+(1/3)×sin(2π×150t)，采样频率为12 800 Hz，采样时间为0.2 s，对其进行EMD分解，得到各IMF分量见图2．再对各IMF分量进行Hilbert变换，得到相应的瞬时频率和瞬时幅值，见图3．

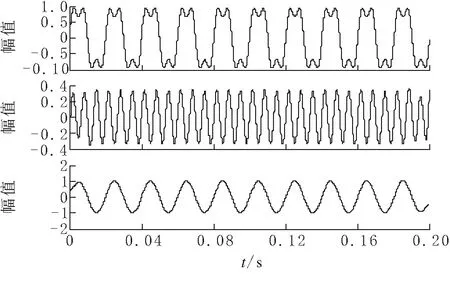
图 2 平稳谐波信号的EMD分解图

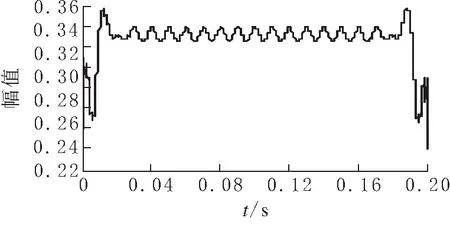
(a)imf1分量瞬时包络

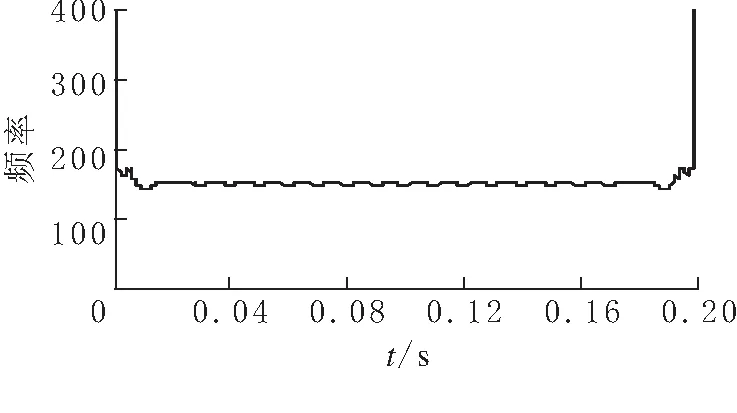
(b)imf1分量瞬时频率

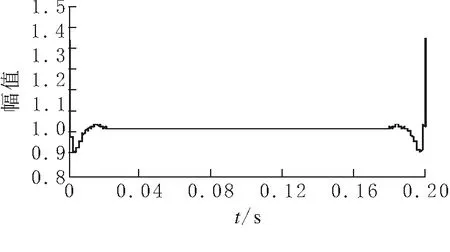
(c)imf2分量瞬时包络

(d)imf2分量瞬时频率图 3 平稳谐波信号的各IMF分量的Hilbert变换结果

由图3仿真结果可知，谐波信号中含有频率为150 Hz和50 Hz的分量，即含有三次谐波和基波，其幅值分别为0.33和1，结果与所设仿真信号参数一致．

2.2 突变谐波信号的分析

HHT谐波分析方法对突变扰动信号同样具有很好分析和处理能力，设仿真信号为突变信号，其表达式为(9)式所示

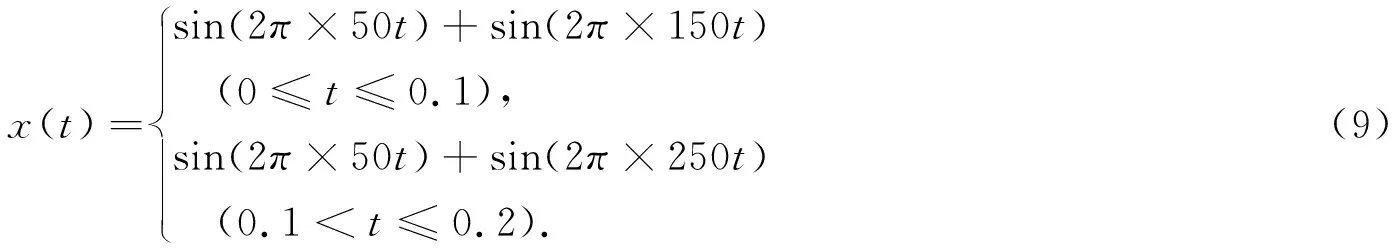
采样频率为12 800 Hz，采样时间为0.2 s，对其进行EMD分解得到各IMF分量及余项如图4所示．由图4可知基波和谐波与输入信号是一致的．

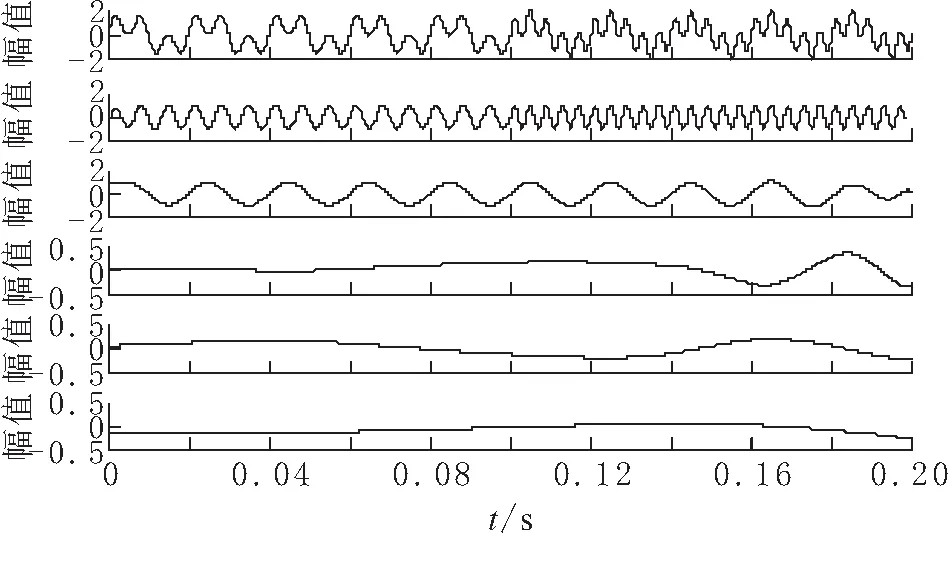
图 4 突变谐波信号的EMD分解图

将得到的各IMF分量进行Hilbert变换得到的瞬时频率和瞬时幅值如图5所示，信号所含频率成分有50 Hz、150 Hz和250 Hz，对应的幅值均为1．并且从IMF1的瞬时频率和瞬时幅值可得信号突变时刻为0.1 s．由此表明，HHT不仅可以得到谐波信号的幅值和频率，而且能够准确地辨别谐波信号的突变时刻．

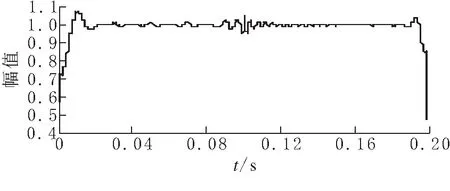
(a)imf1分量瞬时包络

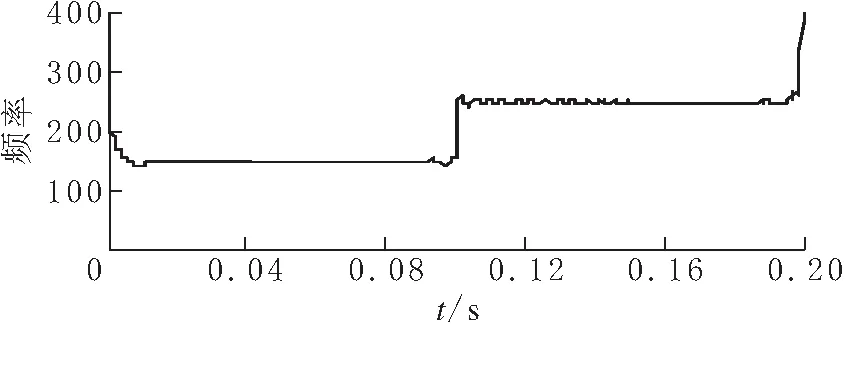
(b)imf1分量瞬时频率

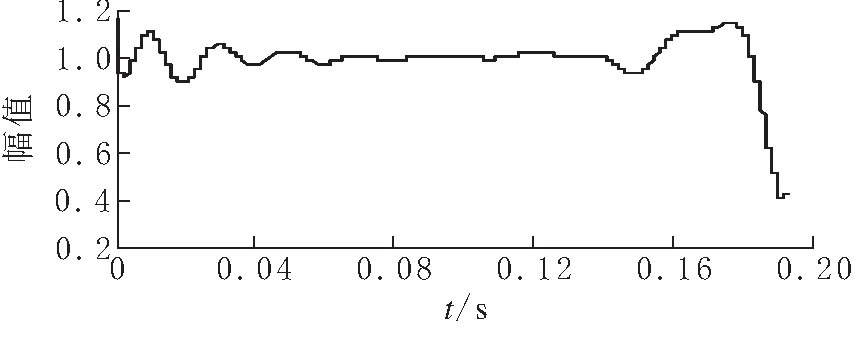
(c)imf2分量瞬时包络

(d)imf2分量瞬时频率图 5 突变谐波信号各IMF分量Hilbert变换结果

2.3 电力系统谐波源的分析与仿真

电力电子装置是电力系统中主要的谐波源．通过Simulink搭建三相感性不可控整流桥作为谐波源(图6)．

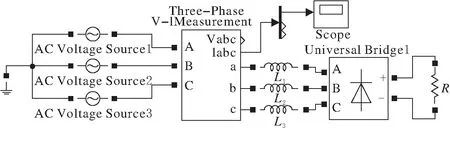
图 6 基于Simulink的谐波源模型

取电感L1=L2=L3=30 mH,负载R=100 Ω，当供电端电压为220 V，频率为50 Hz时，得到A相电流信号的波形见图7．

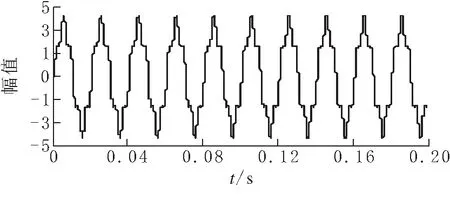
图 7 仿真电流信号

对电流信号进行滤波与采样，采样频率20 000 Hz，时间0.2 s．对信号作HHT分析，得到信号的EMD分解图和各分量Hilbert变换结果分别见图8和图9．

图 8 电流信号的EMD分解图

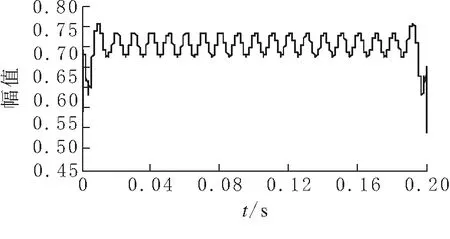
(a)imf1分量瞬时包络

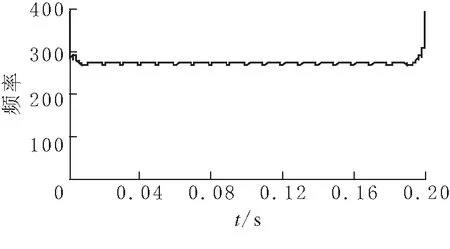
(b)imf1分量瞬时频率

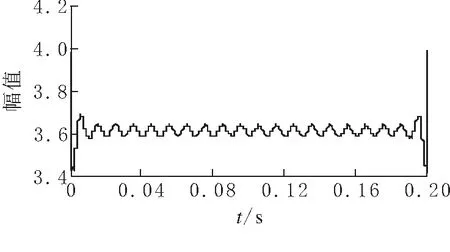
(c)imf2分量瞬时包络

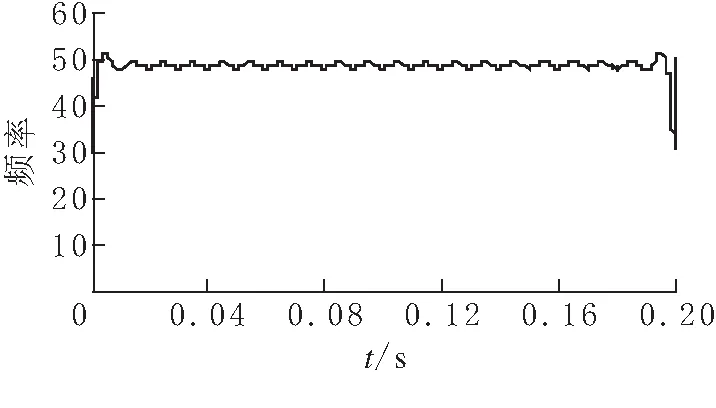
(d)imf2分量瞬时频率图 9 电流信号各IMF分量Hilbert变换结果

根据仿真结果，分析出信号中基波分量的幅值为3.65，谐波频率为250 Hz、幅值为0.71，这与理论谐波次数6k±1(k为整数)相一致．而且通过HHT算法得到的是谐波信号的瞬时幅值和瞬时频率，相对于传统的FFT算法，HHT算法更能反映出信号的幅值与频率随时间变化的关系．

3 结束语

HHT算法对电力系统谐波分析的仿真结果表明，该算法既适于稳态谐波信号分析又适于非稳态谐波信号分析，而且可以准确地得到谐波信号中各次谐波的频率和幅值．对于信号的波动能准确得到波动时间，比较适合时变信号的分析．并且用此方法得到每个单谐波分量的瞬时频率和幅值是随时间变化的，得到的瞬时参数更精确，为电能质量问题提供了分析依据．

[参考文献]

[1] 刘德利.HHT算法及其在电力系统中应用研究[D].哈尔滨：哈尔滨工业大学图书馆,2011.

[2] 李小龙.基于HHT的电力系统谐波检测方法研究[D].长沙:长沙理工大学图书馆,2012.

[3] 姚 强.基于FPGA的电力系统谐波检测系统的研究与设计[D].南京：南京理工大学图书馆,2012.

[4] Norden E.Huang. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc R Soc Lond A,1998:903-998.

[5] 李文帆.基于HHT的电能质量检测系统研制[J].电力系统保护与控制,2011,39(23):123-127.

[6] 李天云,超 妍.HHT方法在电力系统故障信号分析中的应用[J].电工技术学报,2005,20(06):87-91.

[7] 宋明零,周力行.HHT与傅立叶变换在电网故障分析中的仿真比较研究[J].电瓷避雷器,2011,12(06):21-30.

[8] 江 辉.基于希尔伯特-黄变换的电压闪变测量方法[J].电网技术,2012,36(09):250-256.

[9] Zhong Wu. Some considerations on physical analysis of data[J].Advances in Adaptive Data Analysis,2011, 3(01):95-113.

[10] Gabriel Rilling. One or two frequencies? The empirical mode decomposition answers[J]. Signal Processing, 2008,56(01):85-95.

[11] 王 群.电力系统谐波分析算法研究[D].东北大学图书馆，2009.

[11] 肖儿良.改进的HHT算法在电力系统谐波检测中的应用[J].电力学报,2012,27(12):119-122.

[12] 李婉娉.基于HHT的微网中谐波与间谐波的检测与分析[J].电网技术,2012,20(01):20-24.