一维非齐次弦振动方程cauchy问题的解法

张丹丹

(湖北文理学院 数计学院，湖北 襄阳 441053）

0 引言

弦振动方程又叫一维波动方程，其分为齐次波动方程与非齐次波动方程两类[1]。对于非齐次波动方程的cauchy问题，在本文中我们首先由线性叠加原理，将问题转化为两个定解问题的求解，其中一个为求解齐次波动方程的cauchy问题，另一个问题的求解我们除了用特征线法和算子法[2]外还可以运用green积分法以及齐次化原理。特征线法是将方程作特征变换，再沿特征线积分。算子法如上转化为求关于一阶线性偏微分方程的特解问题。green积分法是运用green公式对特征线与X轴围成的三角区域进行积分。green积分法则是对公式的扩展运用。对于非齐次波动方程的cauchy问题，将方程化为对于齐次波动方程的问题是常见的思想，而齐次化原理[3]正好就解决了这个难题。

1 非齐次弦振动方程的cauchy问题

下面是非齐次弦振动方程的cauchy问题的一般形式：

由线性叠加原理，我们知道，问题（1）的求解可以转化为如下两个问题的求解，即若函数 u1(x，t)，u2(x，t)分别为定解问题：

则函数u=u1+u2为定解问题（1）的解。

而由D′Alembert公式可求得（3）的解，则求（1）的解即可转化为求（2）的解，我们一共有4种方法求（2）的解，下面将一一作详细的介绍：

1.1 齐次化原理：

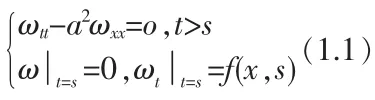
设 t′=t-s，利用 D′Alembert公式求（1.1）式的解为：

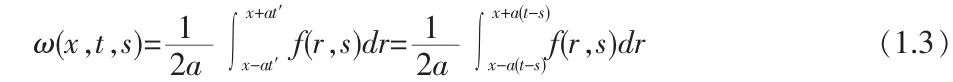
代入（1.2）式得

其中G为ros平面过点（x，t)向下作两条特征线与Or轴所夹的三角形区域。

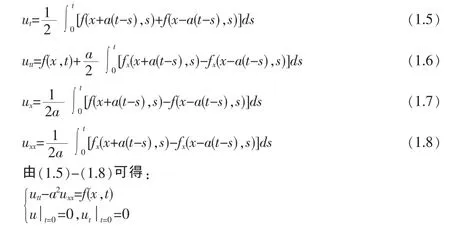
定理证毕。

1.2 特征线法：

将（1.9）积分可得

其中积分下限是任意的常数，它相当与积分常数[5]。

任意给定点(x0，t0)，设：

则（1.10）式有特解：

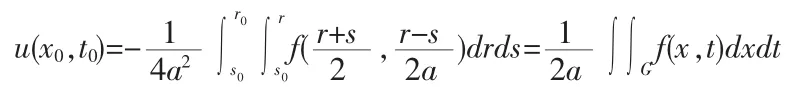
其中G为ros平面过点（x，t)向下作两条特征线与Or轴所夹的三角形区域。

1.3 算子法

将方程 utt(x，t)-a2uxx(x，t)=f(x，t)写成如下算子形式：

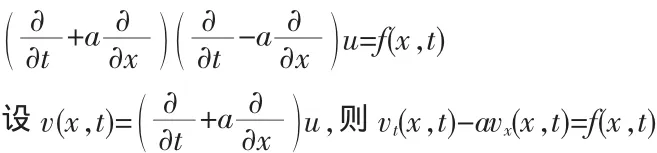
由此得到如下一阶线性偏微分方程：

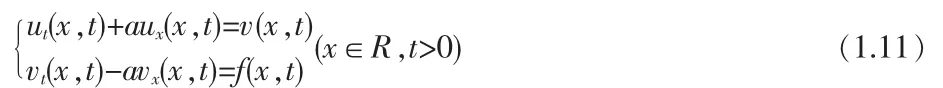
方程（1.11）可化为

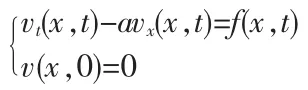
运用齐次化原理得：

1.4 green积分法

设(x0，t0)是区域{(x，t)｜-∞0}内的一点，过(x0，t0)向下作两条特征线与OX轴分别相交于点(x0-at0，0)与点(x0+at0，0)，且设这两条特征线与OX轴围城的三角形区域为G，边界为l0∪l1∪l2

在G上积分问题中的非齐次方程，我们有：

由此得出非齐次弦振动cauchy问题（1）的解为：

1.5 平行四边形性质：

设u(x，t)为弦振动方程utt-a2uxx=f(x，t)在平面区域Ω中的一个古典解，而∏为各边均为弦振动方程utt-a2uxx=f(x，t)特征线的一个平行四边形（包括平行四边形内部），其顶点依次为A，B，C，D.则u(A)+u(C)=u(B)+u(D)

解：取A的坐标为(x′，t′)，过点A作弦振动方程的特征线.

由于弦振动方程为utt-a2uxx=f(x，t)，其特征方程为(dx)2-a2(dt)2=0

即其特征方程为x+at=c1，x-at=c2.

在 x+at=c1和 x-at=c2上分别取两点 BB(x′+ar，t′+r)，DD(x′-at，t′+t)，

则 C 点坐标为(x′+ar-at，t′+r+t)

由D′Alembert公式解U在对顶上的值的和是相等的。

即：u(A)+u(C)=u(B)+u(D)

2 应用举例

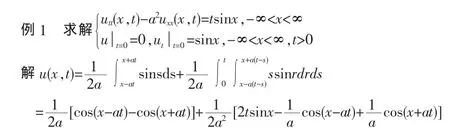
注：弦振动方程具有平行四边形性质，运用该性质也可求解弦振动方程。

解：由弦振动方程的平行四边形性质知：

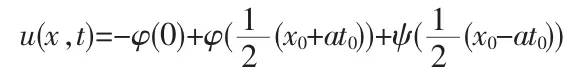
[1]谢鸿政，杨枫林.数学物理方程[M].科学出版社，2003.

[2]张丹丹.一维波动方程问题解[J].科技信息，2012，33:44-37.

[3]汪德新，数学物理方法.2版[M].华中科技大学出版社，2001：150-155.

[4]F.John.Partial Differential Equations.(4th ed.)[M].Springer.

[5]A.Friedman.Partial Differential Equations of Parabolic Type[M].Prentice-Hall.1964.

[6]D.Gilbarg and N.Trudinger.Elliptic Partial Differential Equations of Second Order(2nd ed.)[M].Springer,1983.