基于腰部加速度计的行走能耗建模实验研究

孙 泊，刘 宇，庄 涛，孙明运，李旭鸿

1.Liaocheng University，Liaocheng 252059，China；2.Shanghai University of Sport，Shanghai 200438，China；3.Zhejiang Research Institute of Sport Science，Hangzhou 310036，China.

许多方法可以获取身体活动的能耗，如调查表、心率监视器（利用心率计算能耗）、雷达、双标水技术，但各有优、缺点［18］。到目前为止，加速度计已成为测量大样本人群体力活动最适合的方法之一。加速度计小而轻，不具有侵入性，可以直接测定身体活动的强度和持续时间［3，4，19］。

由于运动方向不能从加速度计中直接获取，但是当行走和跑步的循环模式、直线方向、行走速度是稳定状态时，分析和解读步态数据变得相对容易。在这种情况下从理论上看，正、负加速度绝对值应该是相等的，加速度代数和趋向于零。许多研究用加速度的均方根（RMS）转换数据，建立RMS和其他步态参数相关关系，不管怎样，由于原始加速度值均数等于零，RMS 就成为和标准差等价的测量离散程度的指标［12］。Bouten等人研究发现，在行走过程中腰部三维加速度3 个方向加速度积分值与活动能耗［1－3］、活动强度［8］呈较高的相关关系。步态周期性的运动模式隐含着每一步都有加减速，这种特定的活动为加速度计的使用提供条件。许多研究显示，加速度和身体活动的能耗存在显著的相关关系［5］，同时，有研究表明，加速度计测量值比心率更能有效地反映日常运动时的能耗［11］。

Schutz等人［19］利用放在腰椎位置的前、后方向的单轴加速度计推估出运动速度模型（r＝0.93），并计算出在日常生活运动中加速度值的均方根和能耗之间的回归模型。他采用个性化的建模方式，不管是在实验室还是在自由生活的环境，Schutz认为，固定在躯干的便携式单轴加速度计能够准确地预测行走的速度，用于能耗评定的同时，还可以评估日常生活的活动方式。Kumahara 等人［7］使用代谢室（respiratory chamber）验证只有一个垂直方向的单轴加速度计测量人体能量消耗的情况，发现尽管加速度推算的能耗低于实际测量值，但加速度计测量能耗是比较可靠的。

近年，一些商用的能耗仪（监视器）利用加速度测量原理计算能耗应用广泛，如ActiGraph 以及Tritrac－R3D，这种被称为加速度计的能耗仪，包括加速度计（或称为加速度传感器）、储存卡、能耗估算模型以及液晶显示屏等，它们通过固定在人体上（腰部、手腕或足底等位置）的加速度计测量数据计算人体运动路程、步速和能耗等［17］。然而，一些商用的监视器数据处理的算法并不为消费者所了解，此外，利用加速度计评价身体活动还没有具体标准［15］。因此，有必要了解这些能耗仪的运算模型怎样建立，如何估算人体活动的能耗。本研究主要目的是考察腰部加速度及其衍生变量中哪些能更好估算行走的能耗，是加速度信号的均方根值还是积分值？在使用单轴加速度传感器估算人体运动的速度以及能耗时垂直轴和前后轴哪个轴更敏感、更精确？

1 研究方法

1.1 研究对象

选取普通大学生志愿者作为受试者8 名，身体健康，下肢没有病史，受试者的年龄为20.89±0.60岁，身高为171.89±3.37cm，体重在63.00±2.18kg，BMI（Body Mass Index）为21.34±0.90kg／m2，从受试者的BMI来看，受试者的体重处于正常范围（18.5～23.9kg／m2）。实验前让受试者了解整个实验过程以及应该注意的问题。

1.2 实验仪器

H／P／COSMOS，Gaitway一维测力跑台（德国）1 台，用于控制运动速度；测试前对跑台的带速进行标定。使用运动心肺功能测试仪Vo2000（美国），采集耗氧量（ml／min）、能耗消耗（kcal／day）；心率遥测仪POLAR 表（芬兰）用来测定心率；由于走、跑主要是在人体矢状面的运动，在此选择两轴加速度计（biaxial accelerometer）1 个（德 国Biovision 公司）进行测量，量程±20g，14×14×14 mm，重量20g，信噪比（信号／噪音）小于1μV，带宽：DC－500 Hz，放大频率（gain）：100～1 000，输入阻抗：10GOhm，共模抑制比（CMRR）：130dB，采样频率1 000 Hz，采集软件DASYLab 10.0；秒表1块。

1.3 实验方案

首先测量身高、体重、腿长，佩戴仪器装备，受试者静坐休息5min，然后测量安静时的能耗Erest（Resting Metabolic Rate）与心率，然后熟悉跑台至少6min［9，10，22］，休 息 至稳定状态。稳定状态判断［10，16］：1）心率达到安静时心率±5%；2）耗氧量和安静状态下一致；3）受试者自身的感觉。

跑台速度设定：行走速度为0.6m／s、0.8m／s、1.0m／s、1.2m／s、1.4m／s、1.6m／s、1.8m／s和2.0m／s；实验过程实时观察和监控受试者的心率、耗氧量、呼吸商（维持在1以下）。能耗的采集过程中采用速度逐步递增的方式，每一个速度档次测试时间至少6 min，耗氧量曲线以及心率曲线稳定时间为3min，采用后2min的能耗参数进行统计计算。受试者疲劳时停止实验并进行休息，疲劳判断：心率检测、自我感觉、外表观察。在跑台上要求受试者的头部保持一定姿势，视线方向向下与眼睛水平面夹角15°附近［21］，尽量与日常生活中的行走方式一致。

加速度计固定在背后第一骶椎上缘位置。在正常的行走中，健康人上体在矢状面和额状面的旋转分别达到1°～2°和2°～4°［6］。加速度计的X轴的正方向对准身体前进的方向，Z轴的正方向对准在身体的垂直轴向上的方向，测量第一骶椎上缘位置前后方向和垂直方向的加速度；加速度放在此位置的好处是对于正常人来说在走跑运动的时候躯干的前后倾的角度较小，扭转角度也比较小，这样加速度计前后方向的加速度比较接近人体前进的方向，加速度计上、下方向基本与重力加速度的方向一致，再没有方向传感器的情况下，这应该是比较好的选择。

1.4 数据处理

数据处理采用Matlab 7.0编程计算，采用单因素回归分析，使用Matlab 7.0的Stepwise Regression工具箱进行统计。运动时能耗比体重标准化处理［20］：AEE＝（Egross－Erest）／M（单位：cal／kg／min），其中，AEE 是运动时的净能耗（Active energy expenditure），Egross是运动时的总能耗（Gross energy expenditure），Erest是受试者静坐时的能耗（Rest energy expenditure），M 为体重（Mass）。加速度积分值的单位为：counts／min，为每分钟的加速度积分值［3］，是与能耗值截取时间相对应的一段时间的平均值。

信号处理，采用二阶截止频率17 Hz巴特沃斯低通滤波器对原始信号进行滤波，加速度原始信号积分值用来计算平均加速度。加速度信号去趋势前后比较如图1 所示，黑色的曲线是去趋势前的加速度信号，灰色的曲线是去趋势后的加速度信号，去趋势后的加速度信号曲线向零点偏移，可有效地去除重力加速度的影响，使用公式（1）和（3）数据处理方式为去趋势处理。

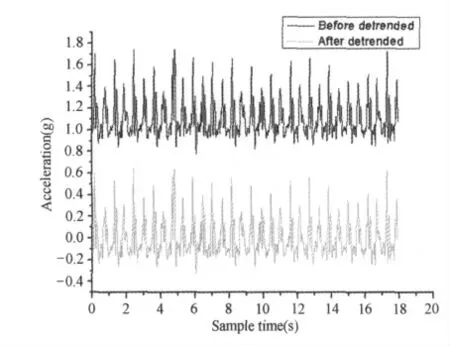
图1 本研究垂直方向加速度去趋势前、后比较示意图Figure 1.Comparison of Vertical Acceleration before and after Detrended

使用下面计算公式进行数据处理：

垂直方向或前、后方向的去趋势后加速度均方根值（RMS）［14，19］：

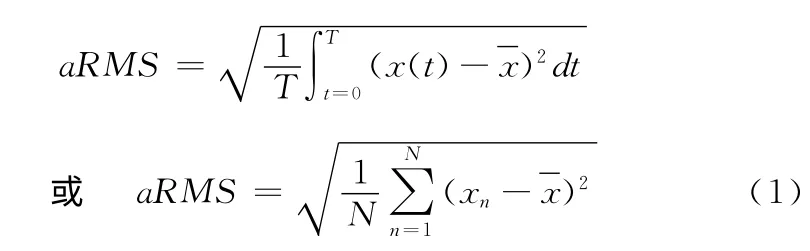
前、后方向的加速度的均方根（RMS）计算公式：

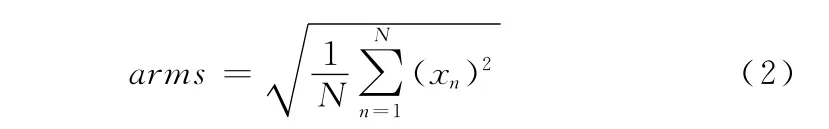
前、后方向或垂直方向的加速度去趋势以后积分计算公式：

前、后方向加速度直接积分计算公式：

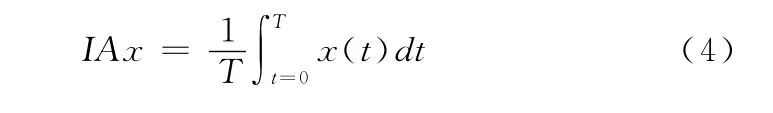
垂直方向加速度去重力加速度后积分计算公式：

加速度衍生变量的表示如下：

zRMS：去趋势（减去均值）以后的垂直方向加速度的均方根，单位：g；

xRMS：去趋势（减去均值）以后的前、后方向加速度的均方根，单位：g；

xrms：未去趋势前、后方向的加速度均方根值，单位：g；

Iaz：垂直方向加速度去趋势以后每分钟的积分值，单位：counts／min；

Iax：前、后方向加速度去趋势以后每分钟的积分值，单位：counts／min；

IAtot：（IAtot＝Iaz＋Iax）前、后方向加速度去趋势后积分值与垂直方向的加速度去趋势以后积分的和，单位：counts／min；

IAz：垂直方向的加速度减去重力加速度以后的每分钟积分值，单位：counts／min；

IAx：前、后方向的加速度每分钟积分值，单位：counts／min；

IAAtot：（IAAtot＝IAx＋IAz）前、后方向加速度积分与垂直方向的加速度积分的和，单位：counts／min。

统计结果变量的表示：Intercept：截距；RMSE：均方根误差；Coeff.：系数（斜率）；R－square：复相关系数；Adj Rsq：调整后的复相关系数。

2 结果与分析

2.1 净能耗与加速度均方根、积分值之间相关关系

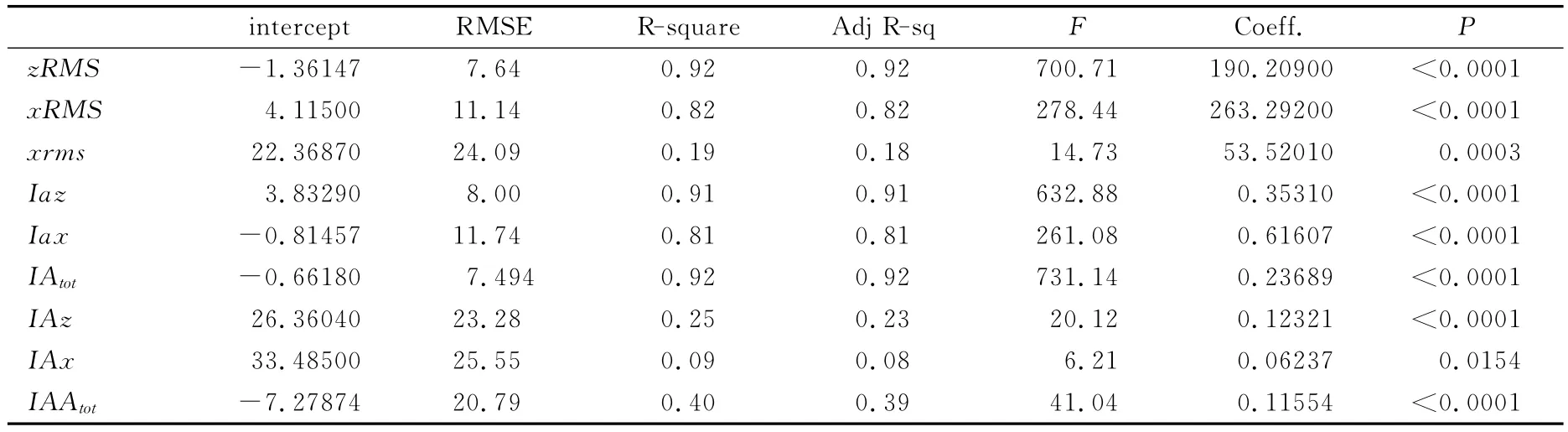
表1 本研究行走的净能耗与加速度衍生变量之间的线性回归结果一览表Table 1 Linear Regression Variables between Walking Net Energy Expenditure and Acceleration Derived Variables

表1列举了因变量（行走时的净能耗）与每个自变量之间的一元线性回归结果，若均方根误差越小、相关系数越大、F值越大，表明2 个变量之间的相关程度越高。从加速度衍生出来的单一变量来看，去趋势以后2 个方向加速度积分值之和（IAtot）与运动的能耗（AEE）之间相关度最高，其中均方根误差最小，复相关系数最大，F值也最大（F＝731.14）（图2）。线性回归方程为：

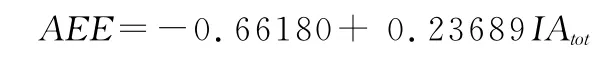
图2 本研究行走的净能耗与去趋势后的加速度积分和之间的相关关系示意图Figure 2.Relationship between the Sum of Detrended Acceleration Integration and Walking Net Energy Expenditure

对于去趋势后垂直方向加速度均方根值（zRMS）与加速度积分值之和（IAtot）相比，2 个变量推估能耗回归方程的复相关系数几乎相同，R－square＝0.92，其 中，zRMS对应的F值为700.71，仅次于IAtot对应的F值（图3），线性回归方程为：

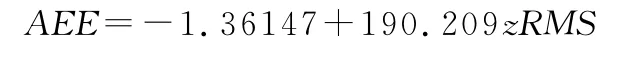
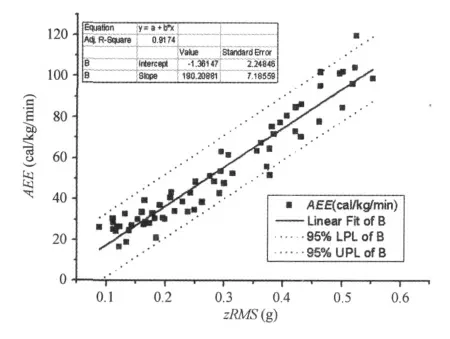
图3 本研究行走的净能耗与垂直方向的去趋势后加速度均方根之间的相关关系示意图Figure 3.Relationship between Walking Net Energy Expenditureand the RMS of Detrended Vertical Acceleration

2.2 速度与加速度均方根、积分值相关关系

表2显示，行走速度与去趋势后的加速度积分和、去趋势后垂直方向的积分值、均方根都有较高的线性关系。行走速度与去趋势后的加速度积分和的散点图见图4，线性回归方程：

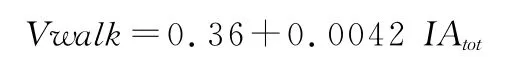
表2 本研究行走速度与加速度衍生变量之间的线性回归结果一览表Table 2 Linear Regression Variables between Walking Speed and Acceleration Derived Variables

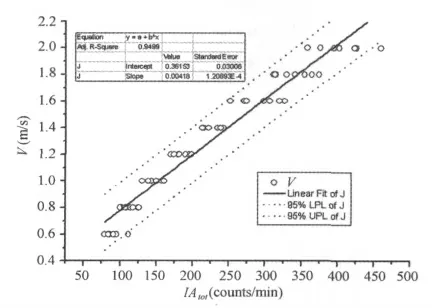
图4 本研究行走速度与去趋势后的加速度积分和之间的相关关系示意图Figure 4.Relationship between Walking Speed and the Sum of Detrended Acceleration Integral Value

行走速度与去趋势后垂直方向的加速度积分之间关系的散点图如图5所示，回归方程：

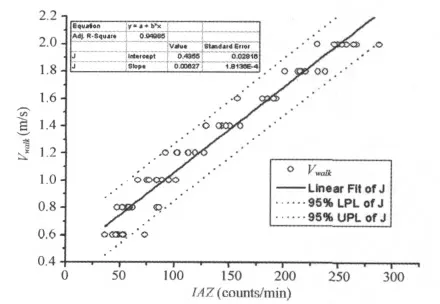
图5 本研究行走速度与去趋势后的垂直方向加速度积分之间的线性相关关系示意图Figure 5.Relationship between Walking Speed and the Integral Value of Detrended Vertical Acceleration

行走速度与去趋势后垂直方向的加速度均方根之间的散点图如图6所示，回归方程：

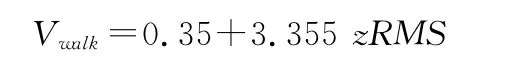
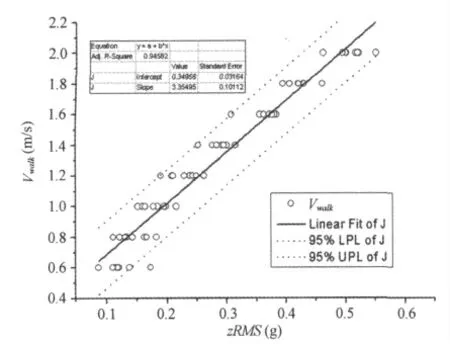
图6 本研究行走速度与去趋势后垂直方向加速度均方根之间的相关关系示意图Figure 6.Relationship between Walking Speed and the RMS of Detrended Vertical Acceleration

3 讨论

走模式下，运动的净能耗与两轴的去趋势后加速度积分的和具有较高的线性关系（R2＝0.92，F＝731.14），其次是去趋势后垂直方向的加速度的均方根（R2＝0.92，F＝700.71）。去趋势后的垂直方向和前、后方向的加速度积分值与运动的净能耗也具有较高的相关（R2＝0.91，F＝632.88；R2＝0.81，F＝261.08）。没有去趋势的加速度均方根以及积分值与净能耗的复相关系数都较低。为什么去趋势以后计算得到的数值与运动的净能耗有较高的相关关系呢？首先，尽管在安装加速度计的时候尽量使2个敏感轴对准人体行进的前、后方向以及重力加速度方向，但是2个轴与受试者前、后方向以及垂直方向仍会存在一定的角度。其次，由于重力加速度的存在，重力加速度在2个轴都存在分量，导致加速度计的敏感轴测量值不完全是所对应的前、后方向以及垂直方向的加速度实际值。再次，受试者佩戴加速度计时，固定可能产生差异；受试者具有个性差异，行走过程中身体重心的起伏以及身体的扭转存在一定个体差异，最终导致数据离散较大。去趋势后可使加速度均值平移到“0”点，加速度计敏感轴的重力加速度分量会得到一定程度的去除，使去趋势后的加速度均方根以及积分值与能耗、速度具有较高的线性相关关系。

Schutz等人［19］利用去趋势这种处理数据方法，使用单轴加速度计，得出前、后方向的加速度均方根能有效推估运动时的净能耗。而Kumahara等人［7］证实了一个垂直方向的单轴加速度计测量能耗的可靠性。针对前人的2种不同的研究结果，从表1知道，去趋势后垂直方向的加速度均方根（zRMS）估算能耗回归方程的复相关系数（R2）为0.92，均方根误差为7.64；而去趋势后的前、后方向加速度均方根（xRMS）估算能耗回归方程的复相关系数（R2）为0.82，均方根误差为11.14，复相关系数越高说明相关性越高，均方根误差越小说明精确度越高，尽管去趋势后的前、后方向加速度均方根与能耗的相关性也较高，但是去趋势后的垂直方向的加速度均方根估算能耗更精确。把加速度信号去趋势后，在前、后方向上以及垂直方向上加速度信号与能量消耗以及运动速度都具有较高的线性关系，如果只使用单轴加速度计的话，垂直方向的敏感轴优于前、后方向的敏感轴。表1显示使用去趋势后的加速度积分变量估算能耗也得出相同的结论。

从理论上讲，只要加速度计的敏感轴对准人体行进的方向，应该是使用没有去趋势的加速度值推估能耗效果更好，但是，实际情况正好相反，在前、后方向上，只使用原始数据与净能耗之间相关关系较低，同样在垂直方向上，去趋势后的加速度积分值推估能耗（R2＝0.92）要比垂直方向的加速度减去重力加速度后的积分值推估能耗（R2＝0.39）精确的多。由于人体行走的能耗与行进速度高度相关［20］，本研究结果表明只要加速度及其衍生变量与能耗相关性较高（表1），也与速度变量有较高的相关性（表2），这也从侧面验证了人体行走的能耗与速度密切相关。

完全校正生活中佩戴的加速度计重力分量几乎是不可能的，影响加速度信号的因素还有：割草机、公交车以及皮肤的震动等。加速度计放置的位置、年龄以及个体对估算能耗的影响都有待于进一步研究。

不足之处在于，跑台是测量步态的比较便利的工具，但在跑台上与地面上的行走步态参数存在一定的偏差，相同运动速度下在跑台上的能耗可能稍高于地面上的能耗［4，13］，本研究中受试者都有跑台上运动的经历，在测试前都经过一段时间来适应跑台，尽量减小跑台与地面上的步态以及能耗的差异，在跑台上与地面上的测试可能不会完全相同，但不会对实验结果造成较大的影响。

4 结论

1.使用腰部加速度计能较好地估算人体行走过程中的速度及能耗。多轴加速度计估算能耗的精度高于单轴。

2.加速度信号去趋势处理以后的均方根值以及积分值与运动速度以及能耗具有较高的线性相关关系。

3.垂直方向以及前、后方向的敏感轴都能较好地估算人体活动的能耗以及步速，但使用单轴加速度计时，垂直方向的敏感轴优于前、后方向的敏感轴。

［1］BOSCH S，MARIN－PERIANU R，HAVINGA P，etal.Energy－Efficient Assessment of Physical Activity Level Using Duty－Cycled Accelerometer Data［J］.Procedia Computer Sci，2011，（5）：328－335.

［2］BOUTEN C V，WESTERTERP K R，VERDUIN M，etal.Assessment of energy expenditure for physical activity using a triaxial accelerometer［J］.Med Sci Sports Exe，1994，26（12）：1516.

［3］BOUTEN C V C，KOEKKOEK K T M，VERDUIN M，etal.A triaxial accelerometer and portable data processing unit for the assessment of daily physical activity［J］.Biomed.Eng（NY），1997，44（3）：136－147.

［4］DAL U，ERDOGAN T，RESITOGLU B，etal.Determination of preferred walking speed on treadmill may lead to high oxygen cost on treadmill walking［J］.Gait Posture，2010，31（3）：366－369.

［5］ESTON R G，ROWLANDS A V，INGLEDEW D K.Validity of heart rate，pedometry，and accelerometry for predicting the energy cost of children＇s activities［J］.J Appl Physiol，1998，84（1）：362－371.

［6］FRIGO C，CARABALONA R，DALLA MURA M，etal.The upper body segmental movements during walking by young females［J］.Clin Biomech，2003，18（5）：419－425.

［7］KUMAHARA H，SCHUTZ Y，AYABE M，etal.The use of uniaxial accelerometry for the assessment of physical－activity－related energy expenditure：a validation study against whole－body indirect calorimetry［J］.Br J Nutr，2004，91（2）：235－244.

［8］KURIHARA Y，WATANABE K，YONEYAMA M.Estimation of walking exercise intensity using 3－D acceleration sensor［J］.IEEE Trans Syst Man Cybern C Appl Rev，2012，42（4）：495－500.

［9］LAVCANSKA V，TAYLOR N F，SCHACHE A G.Familiarization to treadmill running in young unimpaired adults［J］.Hum Mov Sci，2005，24（4）：544－557.

［10］MATSAS A，TAYLOR N，MCBURNEY H.Knee joint kinematics from familiarised treadmill walking can be generalised to overground walking in young unimpaired subjects［J］.Gait Posture，2000，11（1）：46－53.

［11］MEIJER G A，WESTERTERP K R，KOPER H，etal.Assessment of energy expenditure by recording heart rate and body acceleration［J］.Med Sci Sports Exe，1989，21（3）：343－347.

［12］MENZ H B，LORD S R，FITZPATRICK R C.Acceleration patterns of the head and pelvis when walking on level and irregular surfaces［J］.Gait Posture，2003，18（1）：35－46.

［13］MEYER T，WELTER J P，SCHARHAG J，etal.Maximal oxygen uptake during field running does not exceed that measured during treadmill exercise［J］.Eur J Appl Physiol，2003，88（4－5）：387－389.

［14］MOE－NILSSEN R.Test－retest reliability of trunk accelerometry during standing and walking［J］.Arch Phys Med Rehabil，1998，79（11）：1377－1385.

［15］MOTL R W，MCAULEY E，SNOOK E M，etal.Validity of physical activity measures in ambulatory individuals with multiple sclerosis［J］.Disabil Rehabil，2006，28（18）：1151－1156.

［16］PARVATANENI K，PLOEG L，OLNEY S J，etal.Kinematic，kinetic and metabolic parameters of treadmill versus overground walking in healthy older adults［J］.Clin Biomech，2009，24（1）：95－100.

［17］PRILL T，FAHRENBERG J.Simultaneous assessment of posture and limb movements（e.g.，periodic leg movements）with calibrated multiple accelerometry［J］.Physiol Meas，2006，27（10）：47－53.

［18］SCHUTZ Y，DEURENBERG P.Energy metabolism：overview of recent methods used in human studies［J］.Ann Nutr Metab，1996，40（4）：183－193.

［19］SCHUTZ Y，WEINSIER S，TERRIER P，etal.A new accelerometric method to assess the daily walking practice［J］.Int J Obes Relat Metab Disord，2002，26（1）：111－118.

［20］STOQUART G，DETREMBLEUR C，LEJEUNE T.Effect of speed on kinematic，kinetic，electromyographic and energetic reference values during treadmill walking［J］.Clin Neurophysiol，2008，38（2）：105－116.

［21］VALLIS L A，PATLA A E，ADKIN A L.Control of steering in the presence of unexpected head yaw movements.Influence on sequencing of subtasks［J］.Exp Brain Res，2001，138（1）：128－134.

［22］ZENI J A，JR.，HIGGINSON J S.Gait parameters and strideto－stride variability during familiarization to walking on a splitbelt treadmill［J］.Clin Biomech，2010，25（4）：383－386.