人口红利与我国经济发展的实证研究*

□ 郭晓芳

(福建师范大学经济学院，福建 福州 350007)

一 引言

在经济增长理论分析中，人们通常在研究影响经济增长因素的时候将劳动力、资本、技术等基础要素考虑在内，但除此之外，我们也不能忽视因人口年龄结构变化带来的劳动力资源结构不断改善而创造出的人口红利对经济增长的额外促进作用。所谓人口红利，是指一个国家在一个时期内人口生育率的迅速下降在造成人口老龄加速的同时，少儿抚养比亦迅速下降，总人口中劳动年龄人口比例上升，从而在老年人口比例达到较高水平之前，将形成一个劳动力资源相对丰富、抚养负担相对较轻、于经济发展十分有利的黄金时期。在这一时期内，总人口的年龄结构呈现“中间大，两头小”的状态，使得劳动人口比例较高，保证了经济增长中的劳动力需求，社会负担较轻，财富积累速度比较快，对社会经济的发展十分有利。

改革开放30多年以来，我国经济发展取得了举世瞩目的成就，不少学者认为人口红利在这过程中起着重要的推动作用。计划生育政策严格实施以来，我国经济快速发展，我国人口再生产类型亦从“高出生率、高死亡率和低自然增长率”迅速转变成“低出生率、低死亡率、和低自然增长率”的阶段。在这一阶段的转变过程中，总人口形成了劳动年龄人口比重大而少儿人口和老年人口比重小的年龄结构特征，从而使经济增长面临着抚养负担系数下降和劳动力资源丰富的有利人口时机。我国正是抓住了人口红利这一有利的机遇，利用本国的成本优势，对丰富的劳动力资源加以充分的利用，从而促进经济的快速增长。越来越多的国际经验同样证明了人口年龄结构变化和经济高速增长之间表现出了非常强关联性，人口年龄结构转变产生的人口红利给经济增长带来了正面效应。因此，对我国经济发展中存在着的人口红利效应进行研究，挖掘人口红利中的潜力，对于推动我国经济发展具有重要的实践意义。

二 我国人口年龄结构现状分析

社会总抚养比是衡量社会人均劳动年龄人口的抚养负担的指标，也是社会人口红利的表现形式。社会总抚养比等于14岁以下人口数与65岁以上人口数之和除以15～64岁劳动年龄人口数。一个经济体的总抚养比越低，人口红利就越高，意味着劳动力的抚养负担就越轻。国外学者一般认为最适合经济发展的总抚养比应为50% ～60%，这时消费与就业关系最为合理，经济社会发展较为理想，当社会总抚养比下降到50%以下时，则称为人口机会窗口开启，也就是人口红利期的形成。表1列出了我国历年的人口抚养比情况。

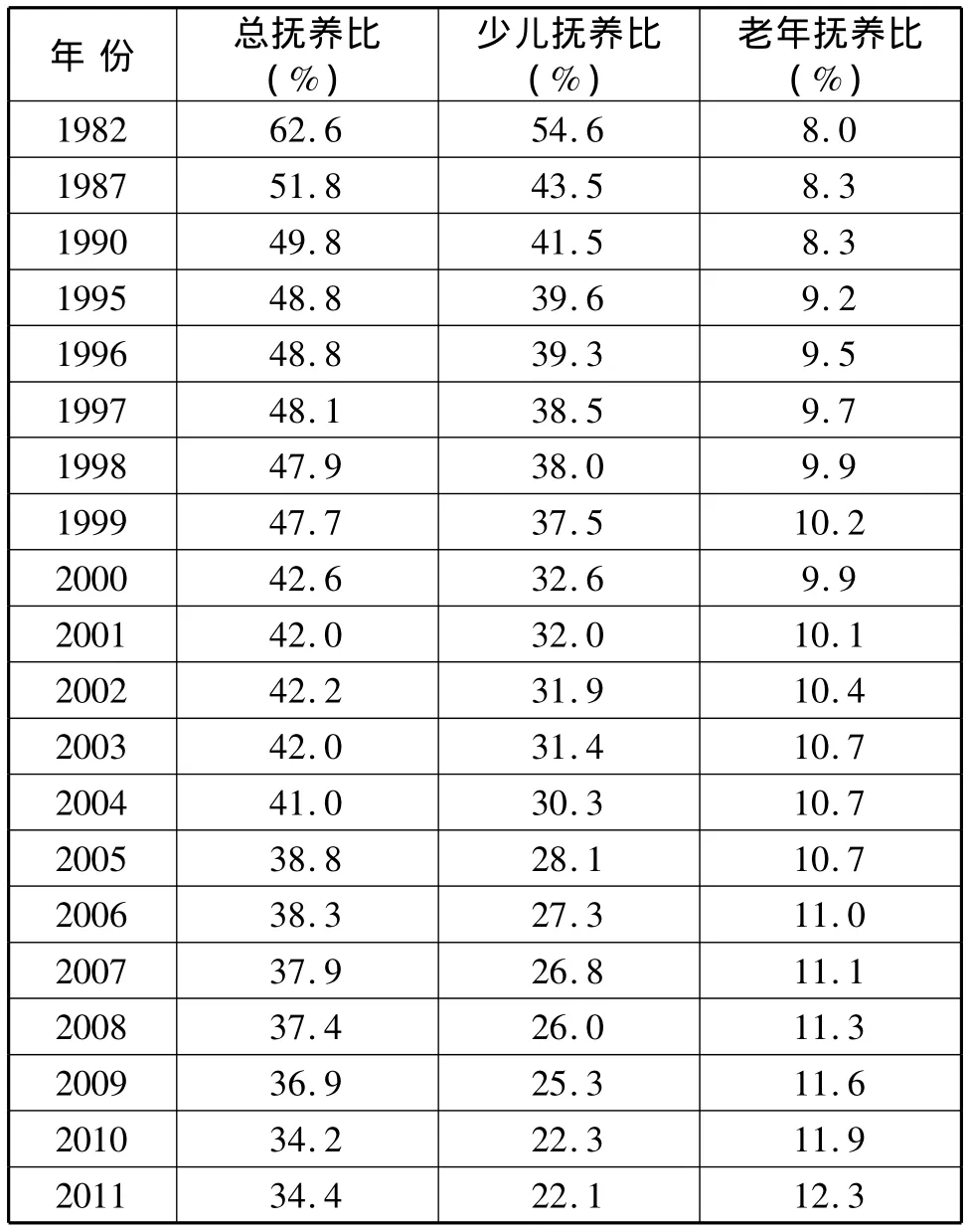
表1 我国历年抚养比情况

改革开放以来，我国经济有了飞跃性的发展，城镇化水平不断提升。而随着计划生育工作的各项服务与措施的进一步落实，晚婚、晚育、少生、优生的生育政策已经深入民心，这都使得群众的生育观念发生了根本性的转变，为稳定低生育水平提供了有利的外部条件。我国在低生育水平保持稳定的同时，人口年龄结构也相应地发生了明显变化。

从表一中我们可以看到，首先，随着我国计划生育政策的有效实施，出生率得到明显的控制，加上群众生育观念的变化，少儿抚养比呈逐年下降的趋势。从1982年到2011年这29年期间，少儿抚养比从54．6%下降到22．1%，下降了32．5个百分点。其次，我国老年抚养比呈逐步上升的趋势。老年抚养比从1982年的8%上升到2011年的12．3%，增加了4．3个百分点。老年抚养比呈逐年提升的现象也从另一个侧面说明了我国已经处于老龄化阶段。根据联合国人口老龄化的标准，一国国家60岁及以上的老年人口占人口总数的比例超过10%或者65岁及以上老年人口总人口的比例高于7%，这个国家就进入老年型社会或老年型国家。从2000年开始，我国65岁以上老年人口占我国总人口数的比例开始达到7%，且此后都逐年提升。根据联合国人口老龄化的标准，我国已明显迈入老龄化社会。最后，我国社会总抚养比逐年降低，从1990年开始社会总抚养比水平就低于50%，我国明显已经进入了人口红利期。此时，我国劳动力资源供给充足，社会抚养负担相对较轻，有利于社会经济的发展。

三 人口红利对我国经济发展的实证分析

(一)模型构建

在构建模型时，首先要考虑解释变量是否能够直接体现我国人口红利现状的各个因素，并且能够增加模型的解释力度。人口红利对我国经济发展的影响途径在不同层面上会有所不同，但最终还是可以归结为储蓄率、总抚养比和就业率这三个方面。本文的研究思路是在理论分析的基础上对各个相关变量进行平稳性检验和协整检验，并根据检验结果建立误差修正模型，最后对回归结果进行分析。

本文选择一下以下变量构建模型:

国内生产总值GDP:用以衡量过我国经济发展水平;国民储蓄率RS:用以衡量我国储蓄相对水平;社会总抚养比GDR:用以衡量我国人口总体中劳动人口负担的指标，是衡量人口年龄结构对社会经济发展影响的重要统计指标;

就业人口数TL:我国就业人口数量。基本模型如下:

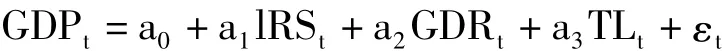
(二)数据来源

为了保证所获得数据的一致性、可获取性，本文所用的数据均来自2012年中国统计年鉴、国家统计局的统计资料，所选数据包括1991～2011年我国GDP，储蓄率RS、社会总抚养比GDR、就业人口数TL等指标的年统计数据。为了减少样本数据时间序列引起的异方差性和避免因数据变化带来的剧烈变动，本文在实际分析时均对相关变量进行了自然对数处理。

(三)实证结果分析

1、简单线性回归。

运用Eviews6软件，采用普通最小二乘法(OLS)对模型进行回归分析，得到:

从上述的回归结果可以看出，R2均大于95%，变量的解释能力较强，拟合优度良好，F检验表明模型整体显著性较好。但是，上述回归结果中D-W值偏小，甚至小于R2，说明了简单线性回归模型可能存在伪回归。因此，我们可对模型中的多变量数据进行平稳性检验和协整检验，以寻找其平稳性，消除伪回归现象。

2、单位根检验。

为了检验所选择时间序列数据的平稳性，避免Granger所提出的的伪回归问题，本文采用ADF检验法对所选数据进行了单位根检验，检验结果见表2。

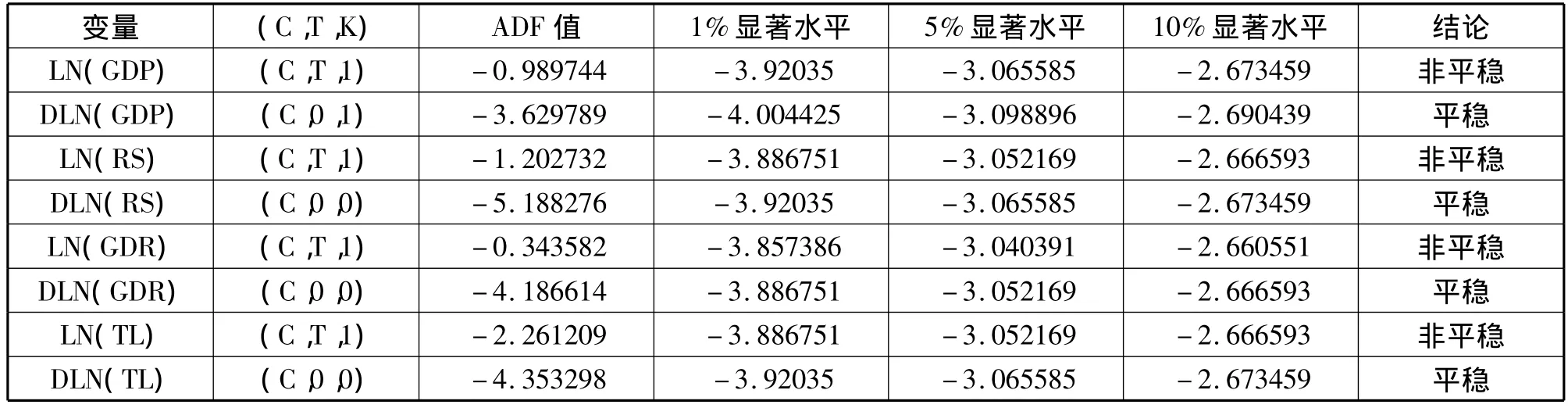
表2 ADF检验结果

由表2的ADF检验结果可知，LN(GDP)，LN(RS)，LN(GDR)，LN(TL)在10%的显著性水平下不平稳，因此，这些原始数据的时间序列是非平稳的。但是对 LN(GDP)，LN(RS)，LN(GDR)，LN(TL)进行一阶差分后的数据 DLN(GDP)，DLN(RS)，DLN(GDR)，DLN(TL)都是平稳的，即各变量都是稳定的一阶单整I(1)序列，满足协整检验的前提，因此可以进一步判断各变量之间的协整关系。

3、Johansen协整检验。

实际应用中大多数的时间序列是非平稳的，但是它们的线性组合却有可能是平稳序列。因此，根据协整理论，各变量间是否存在长期稳定的线性关系，则需要进行Johansen协整检验。对4个主要变量间的Johansen协整检验结果见下表3。

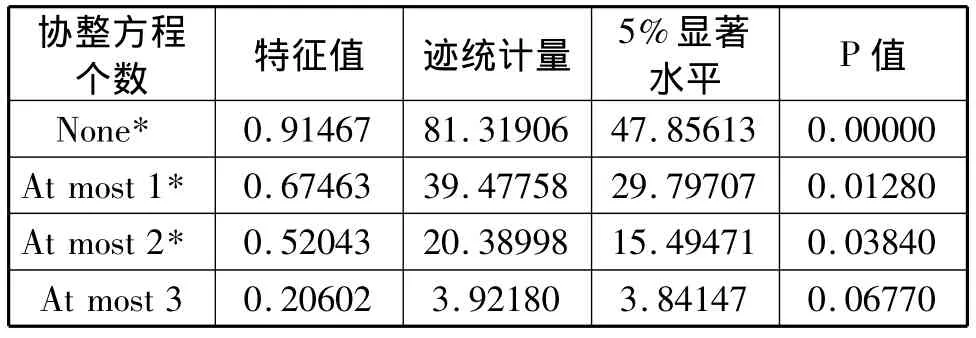
表3 Johansen协整检验结果

由表3的检验结果可以看出，在5%的显著性水平下至少存在两个协整关系，说明我国的国内生产总值、储蓄率、社会总抚养比、就业人口数之间存在着长期稳定的协整关系。

4、误差修正模型(ECM)。

非平稳的时间序列数据可能存在伪回归问题，但是可以通过差分的方法消除其趋势，形成平稳的时间序列，然后进行经典的线性回归分析。而简单的差分线性回归的结果往往只是反映自变量和因变量之间的短期关系，因此，我们可以通过误差修正模型把自变量和因变量间的长期均衡关系再差分回归中描述出来。

由于 LN(GDP)与 LN(RS)，LN(GDR)，LN(TL)之间均存在协整关系，根据对误差修正项的定义，把误差项纳入回归方程中，最终得到以下误差修正模型:

纳入误差项后得到的误差修正模型与简单的线性回归结果相比，模型的R2下降，变量的解释力度有所降低，但是该模型中D-W=1．363054大于1，说明模型中的残差不存在自相关，模型中的伪回归现象被消除了。在误差修正模型中，差分项反映了短期波动的影响，误差修正项ECM系数的大小则反映了对偏离长期均衡的调整力度。误差修正项ECM系数-0．83520体现了对偏离长期均衡的修正，上一期偏离越远，本期修正的量就越大，即系统存在误差修正机制。

5、回归结果分析。

对误差修正模型进行经济意义的解释，可知当国民储蓄率和就业人数增长1%，则国内生产总值GDP分别增长0．27136%、3．42912%，而当社会总抚养比增长1%，则GDP会相应的增长0．04230%。劳动力数量增加对经济增长的带动作用最大，其次为储蓄率，社会抚养比对经济增长的影响并不显著，贡献最小。

四 结论与建议

本文从实证研究的角度考察了人口红利和经济增长之间的关系，实证分析结果表明，社会总抚养比与经济增长之间并没有显著的线性关系，但如果劳动年龄人口能够充分的转变为就业人口，能够被就业市场吸收接纳，则就会对经济增长产生较为明显的推动作用。同时，人口结构变化将会改变国民收入中消费和储蓄的分配比例，使得社会出现高储蓄率，而高储蓄率亦是我国经济快速增长的重要助推力量之一。

目前，我国正处于人口红利时期，但是人口红利效应并不会长期存在。随着人口自然增长率下降、劳动参与率降低等人口结构的变化，我国的人口红利终将逐渐消失，而未来我国经济增长也会因人口红利趋于消失而减速。因此，为应对人口年龄结构变化带来的挑战，挖掘一些有利于经济增长的潜在因素，比如提高劳动参与率与生产率等，采取一系列措施，抓住发展机遇，以避免中国未来的发展进入“老龄化陷阱”或“人口负债陷阱”。

［1］蔡昉．人口转变、人口红利与经济增长可持续性—兼论充分就业如何促进经济增长［J］．人口研究，2004，(2)．

［2］蔡昉．人口转变、人口红利与刘易斯转折点［J］．经济研究，2010，(4)．

［3］马春文，武赫．人口红利对经济发展影响的实证研究［J］．统计与决策，2012，(23)．

［4］张辽．人口红利、结构红利与区域经济增长［J］．中国人口·资源与环境，2012，(22)．