数学文化在实践中的渗透应用——以微积分及教学为例*
2013-11-09肖勇
□肖勇
(宁德职业技术学院,福建 福安 355000)
数学文化不仅包涵数学的知识成分 (命题、方法、问题、语言),也包涵数学的观念成分(数学的精神、思想)。对数学文化的认识需要积极地探讨,形成优质的数学文化理论和数学文化思想。微积分数学文化在数学文化形成中的价值是不可忽视的,微积分数学文化的数学思想可以提高学生的文化素养,学生需要提高运用微积分数学文化来提高数学文化认识。
一 微积分数学文化在日常生活中的应用
一般人们一提起数学,都会用抽象、精确等等词来形容,仿佛它是一座不可逾越的高山。然而,随着社会的进步,科技的发展,数学方法比任何一种科学方法的应用范围都更为广泛,或者说,任何一门学科的发展都必须引进和应用数学方法。可以说,目前只存在尚未运用数学方法的领域,而不存在不能运用数学方法的领域。许多相同形式的数学模型可用于不同的实际问题,并且具有重要的类比和借鉴意义。
在人们的日常生活中,经常接触到的是具体的极限、连续与间断问题。例如在购买商品时,当某种商品的价格不变时,购买的商品数量X,就决定了应该支付的货币Y,即Y=f(x)。如果某种商品的单价为P,则无论要购买多少商品,对应于某商品数量x的每个变动△x,就会有相应的支出额y的变动△y。这些在我们平时都习以为常的买卖过程中,其实就蕴涵了很多的数学知识在里面。再如,公路运输中,当运距在10公里以内时,运价要高一些,10公里至100公里则要低一些,100公里以上的长途运输运价就更低一些。假设10公里以内的运价为5元 /吨公里,10公里至100公里为3元/吨公里,100公里以上为2.5元/吨公里、并设运输工具的载重量都是1吨。则此时,作为一个公司的老板,就必须考虑如何分配货物的运输,才能使得总收益减去总成本后的总利润最大。这些问题的解决,无不体现微积分数学文化在实际应用中的价值[1]。
微积分的数学文化在各方面的应用越来越广泛,比如在养老金领域、贷款领域、医保领域都发挥重要的作用,所以,各种各样的贷款方式铺天盖地,如何选择一种既实惠又符合自己实践能力的贷款方式,成为想贷款买房的人首先应该考虑的事情。
二 微积分数学文化对培养人的能力上的价值
在微积分数学文化的实践中,我们主要是运用“具体——抽象——具体”、“联想 —— 变换 ——联想”、“观察——思考——归纳”、“概念——升华——应用”等方法,经过这样长时间的训练,可以提升人的综合能力,比如在运算能力、自学能力、推理能力、思维方法等方面发挥重要的作用。对人进行知识体系建设具有关键作用,数学模型设计过程中需要把知识和文化结合在一起,把其实际价值结合在一起,提升数学综合应用管理水平[2]。
(一)自学能力的培养
我们知道,微积分数学文化中最基本的概念就是极限的概念,要求一个极限或者证明一个极限问题时,有时候方法会很巧妙。
(二)推理能力的培养
1、极限推理过程中,需要注重函数的连续性,然后通过数学方法的转化,把极限方法得到合理的利用,保证复杂的极限问题得到有效的解决。

2、在极限算法推导过程中需要根据定理和推论的要求,进行各个级别的函数问题分析,通过变换模式可以实现极限的预算,保证极限函数能够在一定的区间范围内进行特征分析。


(三)各种运算能力、运算过程的培养
(三)综合能力的培养
1、导数概念,综合能力培养过程中需要根据数学情况进行变量测算,在各个变量之间形成函数的关系,保证函数具有一定的连续性。同时对函数之间的增量进行分析,增量在商业银行贷款领域得到广泛的应用,要全面理解微积分中增量信息。同时在实践过程中还需要全面掌握边际方面的问题,保证其的变化率符合增强的要求。保证增值率和导数进行关联,从而能够建立有效的微积分方程[3]。
2、微积分方程设计过程中需要根据微积分思想融入在一起,让微元思想能够和数学文化思想结合在一起,在现实生活中发挥重要的价值作用。
3、微积分导数思想和极限设计过程中需要保证利润问题能够很好的解决,现实生活中经常谈到利润,在工作学习中也需要考虑利润、库存、费用方面的问题,根据微积分建立网络,从而能够选择一个最佳路径。
在联系到我们的实际生活,有个新产品销售模型:一种新产品面市,厂家和商家总是采取各种措施,包括大做广告等,促进销售。他们希望对产品的销售速度与销售数量做到心中有数,以便于组织生产、安排进货。我们运用微积分数学文化的知识就可以建立一个数学模型来描绘产品推销速度,并由此分析出有用的结果,以指导生产和销售。
三 微积分数学文化教学实践领域的应用
众所周知,当今数学的应用几乎遍及所有的科技领域,数学的应用不仅在工程技术方面发挥作用,同时也在自然科学方面发挥作用。随着人类社会的不断发展,各类高新技术不断涌现,也提出了更高的要求,由于微积分是数学的重要分支,在高职教学过程中需要发挥关键性作用[1]。
(一)微积分数学文化中的导数理论在学生实践中的应用
例如:高职学生实际学的边际成本C二定义为:增加一个单位产品引起总成本CT的变化。边际收益定义为:附加销售一个商品引起总收益RT的变化。总成本和总收益都是产量Q的函数。所以,边际成本和边际收益在数学上可以表达为各自总函数的导数[2]。也就是:若:Cr=Cr(Q),Rr=Rr(Q),则 Cm数的导数。
(二)微积分数学文化中的极值理论在实践中的应用
例如:设某厂成本C关于产量Q的函数为:C(Q)=5Q+200(元),收人函数为:R(Q)=325Q-Q2(元)。问每批生产多少件产品才能使利润L(Q)最大?
要解决此类高职学生实践中的极值问题,则必须用到微积分数学文化中的极值理论。
解:L(Q)=R(Q)-C(Q)=320Q-Q2=-200
L'(Q)=320-2Q
令 L'(Q)=0,得 Q=160(件)
∴ L"(Q)=-2<0,∴L(160)=25400(元)为极大值,也就是最大值。即每批生产160件产品时,利润最大。
(三)积分数学文化理论在学生实践中的应用
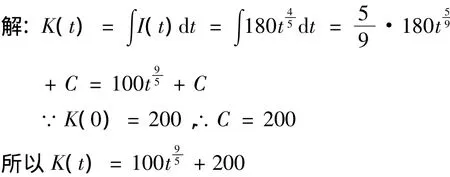
(四)微分方程理论在学生实践中的应用
例如:某市工农业总产值y随时间t的变化率为:-0.002y+0.00203 ,假定y(0)=0,求该市工农业总产值y与时间t的函数关系。

[1]张敬书.数学文化与数学课程改革[J].重庆师范学院学报(自然科学版).2002,(3):85 ~88.
[2]贾晓峰.微积分与数学模型(上)[M].北京:高等教育出版社,1999.
[3]卢达平.《微积分》在经济管理中的应用[J].龙岩学院报,2006,(3):109~111.
