共晶生长理论模型研究现状及应用

赵 素

(上海电机学院 机械学院， 上海 200245)

共晶生长理论模型研究现状及应用

赵 素

(上海电机学院 机械学院， 上海 200245)

综述了共晶生长理论模型的发展，介绍了JH、TMK、KT、LZ和含少量第三组元的过冷共晶生长理论模型在阐述凝固行为、组织形成机制方面的作用。现有的过冷共晶理论模型有一定的局限性，主要表现为非平衡态下溶质截留对晶体生长过程的影响缺乏考虑。

共晶生长理论模型; 定向凝固; 自由凝固

晶体的生长不仅和材料本身的性质有关，同时也取决于固/液界面前沿的溶质扩散、热扩散、表面张力及界面原子附着动力学。深入研究共晶生长规律，控制晶体生长过程，对于构筑理想的材料组织，改善材料性能具有重要意义；因此，人们通过实验研究不断总结出与晶体生长相关的理论模型。虽然理论模型不能完全取代实验，但可以用来指导实验，并不断完善理论假设，从而促进理论和实验的发展。

共晶凝固是从一均匀液相同时析出两个或多个固相的过程，其固液界面形态的建立、演化与相关固相的晶体学特征、固相体积分数、工艺过程参数有关。如果共晶凝固的结果使所有固相在三维空间遵循一定的规律分布，就成为规则共晶；固相的杂乱分布则导致非规则共晶。人们对共晶生长的理论描述主要是针对二元规则共晶合金。1966年，Jackson和Hunt[1]两人首次对二元规则共晶合金的凝固过程进行数学解析，建立了经典的共晶凝固JH理论模型，描述了共晶凝固过冷度、生长速度与规则共晶层片间距之间的关系。但JH模型只适用于较低过冷度下的凝固，随着快速凝固技术的出现，Trivedi等[2]解除了JH模型中生长速度远小于溶质扩散速度的假设，建立了局域平衡凝固的TMK理论模型。随着晶体生长速度的增加，凝固过程愈加远离平衡态。Kurz、Trivedi在TMK模型和非平衡凝固溶质截留理论[3]的基础上，建立了共晶生长的KT理论模型[4]。李金富等[5]在TMK模型的基础上考虑了界面原子附着动力学和过冷合金液相中存在着明显的热扩散，建立了过冷合金共晶生长LZ理论模型。近年来，又发展了添加少量第三组元的过冷共晶合金凝固理论模型[6]。综上可知，根据传热条件，共晶生长的理论模型主要分为2类，分别为定向凝固条件下和自由凝固条件下的共晶生长理论。本文更为全面地对共晶凝固相关理论模型进行介绍。

1 定向凝固条件下的生长理论模型

1.1JH模型

该模型是在近平衡凝固，稳定生长状态下建立的，并假设共晶溶质Péclet数Pe=vλ/(2D)远小于1(v为生长速度，λ为层片间距，D为溶质在液相中的扩散系数)，即共晶层片间距远小于溶质扩散距离。该模型在晶体生长过程中主要考虑了溶质扩散场和凝固界面的曲率效应，从而确定过冷度ΔT、生长速度v和层片间距λ之间的相互关系为

ΔT=ΔTc+ΔTr

(1)

ΔT=K1vλ+K2/λ

(2)

式中，ΔTc为成分过冷度;ΔTr为曲率过冷度;K1、K2是和合金性质有关的常数。

利用JH模型中假定共晶在最小过冷度条件下生长的极限条件，对式(2)中的λ求导数，可得出层片间距和共晶生长速度的相互关系为

λ2v=K2/K1

(3)

JH模型的主要贡献是系统地研究了二元规则共晶组织在生长固/液界面为平界面、慢速凝固情况下，其层片间距的选择机制和共晶组织的形态转变问题。

1.2TMK模型

当凝固速度较大时，JH模型再用来指导共晶生长就会产生较大的误差;因此，1987年，Trivedi等[2]将JH模型扩展到较快速的凝固过程，在近平衡凝固和较大Péclet数的条件下建立了TMK理论模型。该模型认为JH模型中的K1应为共晶Péclet数的函数f(Pe)。该模型主要考虑了2种不同相图情况(任一共晶相的液相线和固相线在共晶温度下的亚稳延长线相互平行；共晶两相的平衡分配系数相等)及在晶体生长过程中溶质扩散场、凝固界面的曲率效应。确定了过冷度ΔT、生长速度v和层片间距λ之间的相互关系为

ΔT=f(Pe)vλ+K2/λ

(4)

利用共晶在最小过冷度条件下生长的极限条件，对式(4)中的λ求导数，可得出层片间距和共晶生长速度的相互关系为

λ2v=K2/f(Pe)

(5)

TMK模型在JH模型的基础上进行了改进，也已得到了广泛地应用。但随着快速凝固技术的发展，可以得到从每秒数微米到每秒数百毫米的共晶生长速度。当共晶生长速度v大于溶质原子的扩散速度vD时，共晶凝固的固液界面将偏离平衡条件，而处于非平衡凝固的状态[3]。局域平衡的破坏意味着液固相线的斜率和溶质分配系数将成为变量。同时，生长速度将会提高，固液相线逐步向T0线靠拢，分配系数趋向于1。为了充分考虑动力学效应对溶质再分配和界面过冷的影响，新的KT[4]模型被提出。该模型考虑到许多共晶体系在高速非平衡条件下仍以共晶方式生长，故该模型是在TMK模型和依赖于生长速度而变化的溶质分配系数、液固相线斜率的基础上而建立的。

1.3KT模型

根据Aziz[3]的研究结果，KT模型在TMK模型的基础上，考虑了生长速度对溶质非平衡分配系数和非平衡条件液相线斜率的影响，建立了非平衡条件下共晶生长理论模型，共晶的过冷度仍由溶质过冷度和曲率过冷度两部分组成。

1.4李周模型

TMK模型虽然对JH模型做了进一步的完善，但不足的是仍未考虑界面动力学过冷的影响。因为形成共晶的相可以有许多种类型，其生长时的动力学特性因晶格构造和界面结构的不同，可以在非常宽的范围内变化[7-8]。同时，随着生长速度的增大，界面动力学过冷将变得越来越重要。鉴于TMK模型的不足之处，李金富等[9]把界面动力学过冷度引入TMK模型中，考察了各种结构类型相形成共晶时的动力学效应，发现动力学相的引入扩大了共晶耦合生长的过冷度范围，降低了共晶生长速度。共晶的过冷度由溶质过冷度、曲率过冷度和界面动力学过冷度3部分组成。

界面动力学过冷直接为液相原子向周围固相表面的附着提供驱动力，可表示为

ΔTk=V/μ

(6)

式中，μ为动力学参数，与相关相的熔化热、熔点温度、界面温度以及特征生长速度等有关。

该模型并没有考虑快速凝固非平衡条件下的溶质截留效应，所以运用在近平衡凝固的情况下比较合理。

2 自由凝固条件下的生长理论模型

2.1LZ模型

在过冷凝固的实验中，热量主要排向周围的过冷液体中；因此，热过冷度应该作为总过冷度的一部分，改变生长行为。李金富等[5]提出了过冷条件下共晶凝固的LZ理论模型。该模型结合了TMK模型和单相枝晶生长的LKT[10]理论模型，在近平衡凝固条件下，考虑了溶质扩散场、热扩散场、凝固界面的曲率效应和界面动力学过冷现象。

界面过冷度由溶质过冷度、曲率过冷度和动力学过冷度3部分组成，共晶两相具有相同的界面过冷度。熔体总的过冷度包括4个部分，即溶质过冷度、曲率过冷度、动力学过冷度和热过冷度。即

ΔTi=ΔTc+ΔTr+ΔTk

(7)

ΔT=ΔTi+ΔTt

(8)

式(7)和(8)中，ΔTt是热过冷度；ΔTi为界面过冷度。

假设枝晶尖端是抛物面形状，则根据Ivantsov[11]分析得出热过冷度(界面温度和远离界面的液体远处温度之差)为

(9)

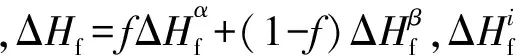
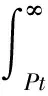
二元共晶合金在过冷熔体中稳态生长，每个相的成长将排出另外一个组元，并在固液界面前沿造成溶质富集区，该富集区的厚度较窄，仅是层片厚度的数量级，它们对于横向扩散造成一定的浓度梯度，这对共晶两相的同时长大是必要的。当枝晶尖端半径远大于层片间距时，其对枝晶形态形成的影响可以忽略，固液界面前沿的热扩散是形成共晶枝晶形态的主要因素[12]。和单相合金相似，共晶枝晶生长使枝晶尖端半径尽可能的小，从而容易排出凝固潜热，但Gibbs-Thomson作用会阻止枝晶尖端半径的减小。热扩散和溶质扩散的扰动随不同的振幅和波长发展，故溶质扩散对枝晶的形态的影响可以忽略，因此可以把枝晶作为热枝晶来处理。

采用边缘稳定性分析及结合LKT模型[10,13]，可以计算出热枝晶尖端半径为

(10)

式中，

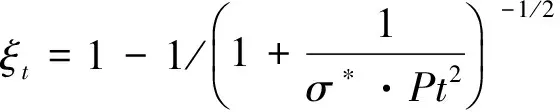
2.2含少量第三组元过冷共晶合金凝固的理论模型[6]

向二元共晶合金中添加少量的第三组元，当第三组元固溶于共晶产物中，不会有新相产生，致使生长界面前沿的较长距离内形成成分过冷区，从而影响到共晶合金的凝固行为。该模型是在LZ模型的基础上建立起来的，其假设共晶界面以树枝状方式进行生长，第三组元的添加不改变共晶两相S/L界面能以及共晶合金熔体中共晶组元的互扩散系数，第三组元在共晶两相中的溶质再分配系数都小于1。这样第三组元在S/L界面前的液相中同时存在垂直于生长界面的扩散以及在两个共晶相之间的横向扩散。在建立模型的过程中，需要同时考虑这两种扩散对共晶合金凝固的影响。

过冷共晶合金熔体凝固时晶体的生长由溶质扩散、热扩散、界面曲率效应以及界面原子附着动力学4个方面因素共同决定，总的熔体过冷度相应包含4个部分，即

ΔT=ΔTc+ΔTr+ΔTk+ΔTt

(11)

共晶枝晶尖端处的成分过冷度ΔTc由共晶主要组元富集导致的过冷度和第三组元富集导致的过冷度共同组成。

计算共晶枝晶尖端半径R时，第三组元的溶质扩散将和热扩散以及界面能共同对共晶枝晶尖端半径的选择起作用。随着第三组元的添加，在共晶生长界面前形成了较长距离的溶质扩散场，枝晶尖端半径随着第三组元添加量的增加而减小。当过冷度足够高时，热扩散将再次成为共晶枝晶尖端半径的主要控制因素，此时，第三组元的影响将减弱。

3 晶体生长理论模型的应用

JH模型可以预测定向凝固过程中一定温度梯度下生长速度和过冷度的关系，通过实验验证了该模型预测结果的正确性[14]。Wei等[15]实验测得低过冷度下共晶的生长速度与过冷度的关系同TMK理论模型预测完全一致，得出了共晶层片生长的临界过冷度和临界生长速度。实验结果验证了理论模型的正确性。当实验条件不能够测量生长速度等参数时，可以利用模型进行预测，得到过冷度分别与生长速度及层片间距的关系曲线。

基于共晶和枝晶竞争生长想法，BCT枝晶生长理论和TMK/KT共晶生长理论模型可以结合在一起，通过比较竞争相的生长速度来计算共晶耦合区[16-19]。共晶耦合区是合金成分和界面温度组成的一个区域，在该区域内，晶体以共晶的方式生长。耦合区表明了大多数共晶合金中层片共晶向反常共晶转变是普遍存在的现象，其可以预测：如果过冷度足够大，反常共晶能够完全取代层片共晶；因此，通过耦合区的计算，可以解释不同过冷度下的组织形成机制等[20-21]。

近年来，Li等[22-23]结合过冷共晶的LZ生长理论、BCT枝晶生长理论模型预测了过冷度和晶体生长速度的曲线关系，解释了反常共晶的形成机制。

4 晶体生长理论模型中尚需解决的问题

生长理论模型的建立到应用再到成熟需要一个过程，即：结合实验结果验证模型的正确性→利用模型预测实验结果→模型的不断完善。迄今为止，过冷单相合金的模型已经得到完善，但对于定向凝固或者自由凝固的共晶合金，当生长速度非常快，必须考虑溶质截留的情况下，溶质分配系数和液相线斜率都不再保持为常数，而是随着生长速度的变化而变化；因此，溶质过冷度的变化会很大，对凝固过程的影响较大[24]。也可以说，当生长速度很快、发生溶质截留的情况下，近平衡凝固条件下得到的生长理论模型不再和实验结果相吻合，此时则需要考虑进一步完善现有的相关理论模型。

[1] Jackson K A,Hunt J D.Lamellar and rod eutectic growth[J].Transaction of the Metallurgical Society of AIME,1966,236：1129-1142.

[2] Trivedi R,Magnin P,Kurz W.Theory of eutectic growth under rapid solidification conditions[J].Acta Metallurgica,1987,35(4)：971-980.

[3] Aziz M J.Model for solute redistribution during rapid solidification[J].Journal of Applied Physics,1982,53(2)：1158-1168.

[4] Kurz W,Trivedi R.Eutectic growth under rapid solidification conditions[J].Metallurgical Transactions A,Physical Metallurgy and Materials Science,1991,22 A(12)：3051-3057.

[5] Li J F,Zhou Y H.Eutectic growth in bulk undercooled melts[J].Acta Materialia,2005,53(8)：2351-2359.

[6] Liu L,Li J F,Zhou Y H.Solidification of undercooled eutectic alloys containing a third element[J].Acta Materialia,2009,57(5)：1536-1545.

[7] Turnbull D.Metstable structures in metallurgy[J].Metallurgical Transactions.B,Physical Metallurgy and Materials Science,1981,12 A(2)：217-230.

[8] Li M,Kuribayashi K.Nucleation-controlled microstructures and anomalous eutectic formation in undercooled Co-Sn and Ni-Si eutectic melts[J].Metallurgical and Materials Transactions A：Physical Metallurgy and Materials Science,2003,34(12)：2999-3008.

[9] 李金富,周尧和.界面动力学对共晶生长过程的影响[J].中国科学·E辑,2005,35(5)：449-458.

[10] Lipton J,Kurz W,Trivedi R.Rapid dendrite growth in undercooled alloys[J].Acta Metallurgica,1987,35(4)：957-964.

[11] Lipton J,Glicksman M E,Kurz W.Dendritic growth into undercooled alloy melts[J].Materials Science and Engineering,1984,65(1)：57-63.

[12] Goetzinger R,Barth M,Herlach D M.Growth of lamellar eutectic dendrites in undercooled melts[J].Journal of Applied Physics,1998,84(3)：1643-1649.

[13] Trivedi R,Kurz W.Morphological stability of a planar interface under rapid solidification conditions[J].Acta Metallurgica,1986,34(8)：1663-1670.

[14] Koçak Y,Engin S,Böyük U,et al.The influence of the growth rate on the eutectic spacings,undercoolings and microhardness of directional solidified bismuthelead eutectic alloy[J].Current Applied Physics,2013,13(3)：587-593.

[15] Wei B,Herlach D M,Sommer F,et al.Rapid solidification of undercooled eutectic and monotectic allo-ys[J].Materials Science and Engineering: A,1993,A173(1-2)：355-359.

[16] Liu X R,Cao C D,Wei B.Microstructure evolution and solidification kinetics of undercooled Co-Ge eutectic alloys[J].Scripta Materialia,2002,46(1)：13-18.

[17] Cao C D,Xie W J,Wei B.Microstructural characterization of cobalt-antimony eutectic alloy droplets solidified in drop tube[J].Materials Science and Engineering A,2000,283(1-2)：86-93.

[18] Yao W J,Wang N,Wei B.Containerless rapid solidification of highly undercooled Co-Si eutectic alloys[J].Materials Science and Engineering A,2003,344(1-2)：10-19.

[19] Yao W J,Wei B.Nucleation and growth of βCu3Sb intermetallic compound in undercooled Cu-31% Sb eutectic alloy[J].Journal of Alloys and Compounds,2004,366(1-2)：165-170.

[20] Han X,Yao W,Wei B.Microstructural evolution of rapidly solidified Co-Mo and Ni-Mo eutectic alloys[J].Journal of Materials Science and Technology,2003,19(6)：553-556.

[21] Liu F,Chen Y,Yang G,et al.Competitions incorporated in rapid solidification of the bulk undercooled eutectic Ni78.6 Si21.4 alloy[J].Journal of Materials Research,2007,22(10)：2953-2963.

[22] Li J F,Jie W Q,Zhao S,et al.Structural evidences for the transition from coupled to decoupled growth in the solidification of undercooled Ni-Sn eutectic melt[J].Metallurgical and Materials Transactions A：Physical Metallurgy and Materials Science,2007,38(8)：1806-1816.

[23] Zhao S,Li J F,Liu L,et al.Eutectic growth from cellular to dendritic form in the undercooled Ag-Cu eutectic alloy melt[J].Journal of Crystal Growth,2009,311(5)：1387-1391.

[24] Zhao S,Li J F,Liu L,et al.Effect of solute trapping on the growth process in undercooled eutectic melts[J].Acta Metallurgica Sinica,2008,44(11)：1335-1339.

Theoretical Models of Eutectic Growth: Progress and Applications

ZHAOSu

(School of Mechanical Engineering, Shanghhai Dianji University, Shanghai 200245, China)

The progress in the theoretical models of eutectic growth is reviewed.The roles of theoretical models (JH, TMK, KT, LZ, etc.) in solidification behavior and formation mechanism of microstructure are introduced.The existing eutectic models have their limitations，mainly in the lack of considerations on the effect of solute trapping on the growth process.

theoretical model of eutectic growth; directional solidification; free solidification

2095-0020(2013)06 -0336-05

O 781

A

2013-07-17

国家自然科学基金资助项目(50571068)；上海高校知识服务平台建设项目资助(ZF1225)；上海高校青年教师培养项目资助(ZZSDJ12006)；上海电机学院重点培育项目资助(12C112)；上海电机学院教师科研启动经费项目资助(13C417)

赵 素(1980-)，女，讲师，博士，主要研究方向为凝固技术与新材料及钢铁材料，E-mail：wellzs@163.com