数据探测法在轴线复测中的应用

卞士挺 楼立志

(同济大学测绘与地理信息学院，上海 200092)

0 引言

地籍测量中，常会遇到一些圆形建(构)筑物如水塔、水池、储油罐等，要准确确定其边界及面积，就必须通过实测圆曲线上若干点来拟合圆方程，即用LS估计求得圆心坐标和圆半径［1-3］。但是在具体的工程测量中，由于环境或人为因素的影响，使得观测值难免存在粗差，若不及时处理粗差，将使LS估计结果受到严重的扭曲。为此，自20世纪60年代起，对粗差的研究一直是测量数据处理的重要课题之一。

Baarda于1967年～1968年提出了测量可靠性理论和数据探测方法，奠定了粗差理论研究的发展基础。Baarda所提出的数据探测法，其前提是假设一个平差系统只存在一个粗差，采用统计假设检验探测粗差，在剔除第一个粗差后，循环迭代继续剔除下一个粗差。

本文将数据探测法应用到轴线复测中，应用结果表明，数据探测法对轴线复测的粗差检测效果非常好。

1 基本原理和过程

在建筑物施工后，原建筑轴线已经被建筑物覆盖(见图1)，P1，P2为建筑角点，但已经修成承重柱子，所以要想测量P1和P2点坐标已经不可能，可通过测量柱子外围1个～7个点坐标，通过拟合方法获得P1，P2点坐标。其本质在于圆曲线拟合。

1.1 圆曲线拟合模型

拟合模型是测量平差中常遇到的一种特殊的函数模型，是一种函数逼近型或统计回归型模型［4］。

在圆曲线或圆柱上采集若干个点(如图1所示)作为独立观测量，通过求该圆的曲线方程可得出圆心坐标及圆半径，由于采集点有误差，各个点并不在同一条圆曲线上，要在这些采集点上拟合出一条最佳圆曲线。

在半径未知的情况下，设采集点个数为m，以圆心的坐标平差值、半径平差值和圆心至各采集点的方位角平差值为参数，圆曲线的参数方程为:

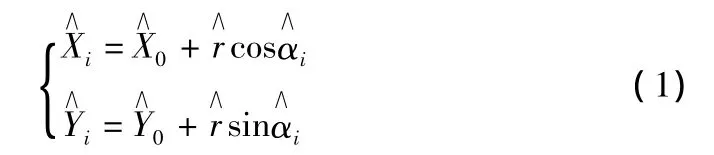
将式(1)线性化，得误差方程为:

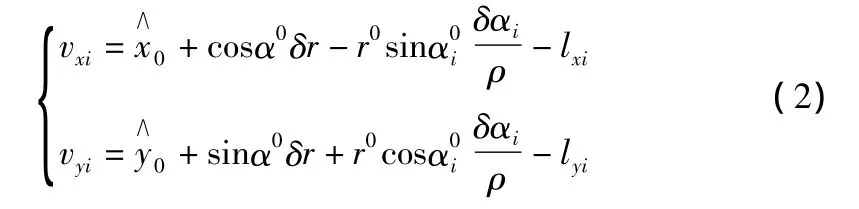
式(2)中:

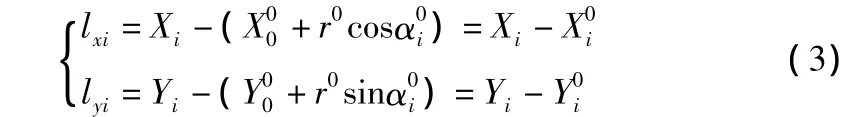
若半径已知，则误差方程如下:

1.2 数据探测法

观测值含有粗差，从其本身来看是无法识别的，要探测和剔除粗差可以根据平差的结果来检验。

测量数据处理中，比较简单的粗差探测方法是残差检验法。

由间接平差原理可知，观测值的改正数V是偶然误差，服从正态分布，即，标准化后则有构造统计量，在显著水平 α 下，拒绝域为若取 95%的置信度，则，所以误差大于 2σ 的事件是小概率事件，当残差大于2σ时可认为该观测值含有粗差。但由于粗差会对平差结果有很大影响，通常情况下会导致验后单位权中误差比正常值大得多，各观测值的残差都受到影响，虽然含有粗差的观测值残差一般会大于没有粗差的残差，但往往会出现不超过2σ的情况，因此残差检验法并不能很好地剔除粗差。经实践验证，荷兰Baarda教授提出的数据探测方法能够有效地探测粗差，已被广泛应用到测量平差中。

数据探测法的前提是假设一个平差系统只存在一个粗差［5，6］，检验探测粗差，从而剔除该粗差。根据间接平差原理，误差方程为:

式(6)中:

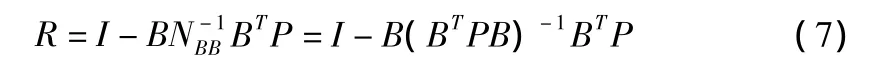
改正数的协因数阵为:

式(7)可写成:

由此可见，R值取决于系数阵B和权阵P，它与观测值无关。在给定观测权的情况下，R反映了网形结构。

R与式(6)是研究粗差探测和可靠性理论的一个重要的关系式。

令:

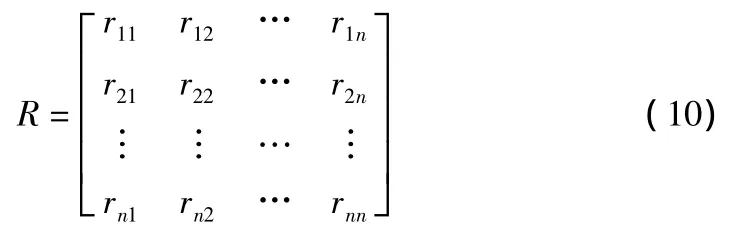
则式(6)可写成显式为:

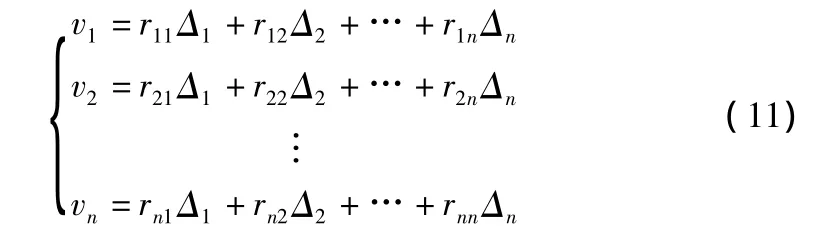
由于|R|=0，所以由上式的n个改正数vi不能解出n个Δi。对式(6)两边取数学期望得:

当Δ仅是偶然误差不含粗差时，E(Δ)=0，故E(V)=0，V是Δ的线性函数，两者的概率分布相同，因此当Δ是偶然误差时，V为正态随机向量，其期望为零，方差为D(V)=。

数据探测法的原假设是H0∶E(vi)=0，即观测值Li不存在粗差，考虑，于是可作标准正态分布统计量:

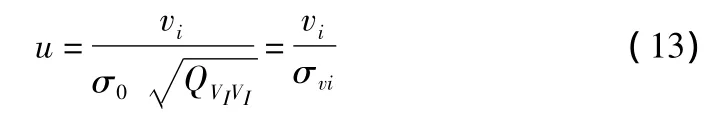
利用数据探测法，一次只能发现一个粗差，当要再次发现另一个粗差时，就要先剔除所发现的粗差，重新平差并计算统计量。逐次不断进行，直至不再发现粗差。

数据探测法并未顾及各改正数之间的相关性，检验可靠性受到一定的限制。

2 算例分析

模拟一组均匀分布的轴线复测观测数据(如图2所示)，采集点为20个，点号顺时针依次为i=1，2，3…，采集精度约为±5 mm的数据。

采用以下三种方法进行解算:

方法1:

在没有粗差的情况下解算。

方法2:

对第1和第12这两点施加±20 mm的粗差，不经粗差检验，采用最小二乘平差进行解算。

方法3:

对第1和第12这两点施加±20 mm的粗差，采用Baarda数据探测法剔除粗差，重新进行最小二乘解算。

三种方法的解算结果如表1所示。

表1 粗差检验拟合精度

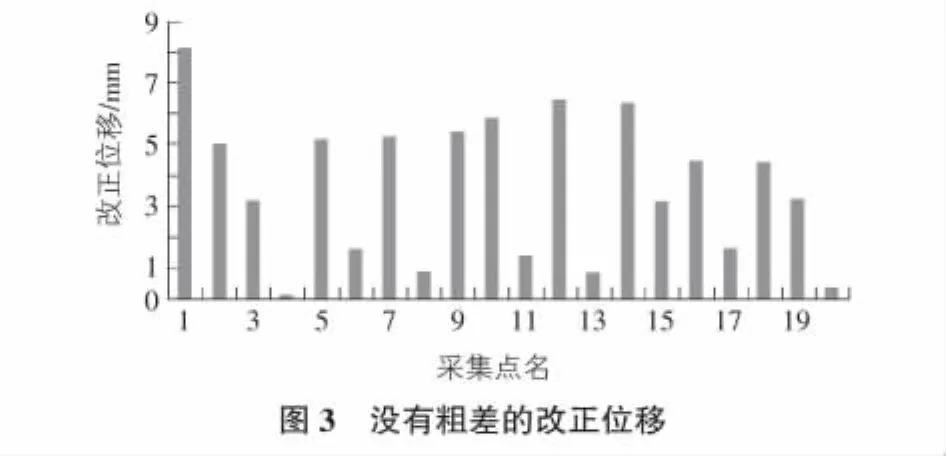
图3反映，在没施加粗差的平差结果中，各采集点的改正数没有出现异常大的数值。

图4反映，当在第1个和第12个点添加粗差后，方法2的解算结果中这两点的改正数比其他点大了好几倍。

图5反映，当在第1个和第12个点添加粗差后，使用数据探测法能发现这两个点存在粗差并进行剔除，解算结果与没加粗差的解算结果基本一致。

表1反映，存在粗差的平差结果失真。一般来说，采集点的精度为±5 mm，那么平差后的单位权中误差应该在±5 mm附近。粗差的存在使得单位权中误差与圆心点位中误差过大，经粗差检验后，结果恢复正常，由此验证了数据探测法的可行性。

3 结语

本文将数据探测法应用到轴线复测中，结果表明，数据探测法能够比较有效地探测出粗差，对检验观测值质量和提高精度有一定的作用，对实际的工程测量数据质量检测也具有一定的参考意义。

［1］潘国荣，谷 川，施贵刚.空间圆形物体检测方法与数据处理［J］.大地测量与地球动力学，2007(3):28-30.

［2］陈基伟.工程测量中一类参数曲线的拟合［J］.大地测量与地球动力学，2007，27(1):100-103.

［3］许正文，姚连璧.基于稳健估计的直接最小二乘椭圆拟合［J］.大地测量与地球动力学，2008(2):77-80.

［4］陈乃辉.随机自变量多项式回归函数的估计问题［J］.系统科学与数学，2009(3):297-308.

［5］彭军还.L1范估计的巴尔达型检验及其可靠性［J］.测绘学报，2015(3):208-212.

［6］方 坤，贺 磊，高俊强.巴尔达粗差探测法在地铁限界测量中的应用［J］.测绘工程，2012(2):47-49.