基于目标舷角分布范围的拖线阵声纳左右舷分辨推理模型

2013-11-09孙永侃林宗祥

指挥控制与仿真 2013年3期

孙永侃，林宗祥，周明

(海军大连舰艇学院，辽宁大连 116018)

被动拖曳线列阵声纳(简称拖线阵声纳)存在左右舷模糊的问题，需要通过母舰的转向机动(简称本舰机动)进行分辨。本舰机动分辨目标左右舷的推理规则为［1］:1)本舰向左转向，若目标舷角增大，则目标在右舷，若目标舷角减小，则目标在左舷;2)本舰向右转向，若目标舷角增大，则目标在左舷，目标舷角减小，则目标在右舷。以上规则是在不考虑本舰转向机动过程中敌我相对运动的理想情况下得到的。实际上，本舰转向完成后测得的目标舷角不但与本舰转向角度大小有关，还与敌我相对运动有关。若运用以上推理规则进行分辨，可能存在误判的问题［2］。本文建立了更加符合实际的模型进行判断。

1 目标舷角分布范围解算模型

本文以目标位于右舷，本舰向左转向为例建立本舰转向完成后的目标舷角分布范围解算模型［3］。如图1所示，T0时刻，本舰位于W0点，航向Cw0，A为拖线阵声纳中心，拖线阵声纳探测中心距我舰距离为d。本舰旋回角速度为ω，旋回半径为r，T0时刻拖线阵测得目标所处舷角为θ0(相对于拖线阵中心A点，目标实际位置为S0)，根据现场水文条件估算敌我距离为R0。此时，本舰开始转向机动，转向角度为α。T1时刻本舰完成转向，此时本舰到达W1点。又经过一段时间航行后，拖线阵被拉直恢复正常听测，T2时刻重新测得目标方位，此时本舰到达W2点，拖线阵声纳中心为B点，则本舰旋回到预定航向所耗费的时间t1为

本舰完成转向到重新测得目标方位所耗费时间t2为

由于目标初始航向未知，假设目标航向在0～360°范围内均匀分布，则经过t1+t2时间后，目标的可能位置分布在以S0(或S0')为圆心，以rq为半径的圆内，称此圆为目标方位圆，则

由几何关系可得

图1 目标在右舷本舰向左转向

在ΔW0AS0中，由余弦定理可得

在ΔW1W0S0中，由余弦定理可得

在ΔBW1S0中，由余弦定理可得

综合以上分析，当目标在右舷本舰向左转向时，T2时刻目标舷角θ1范围为

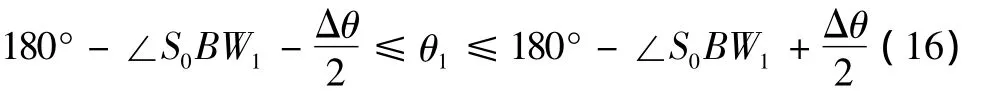
同理，若目标位于本舰左舷，也可求得本舰转向完成后T2时刻目标舷角θ1范围。

2 基于目标舷角分布范围的左右舷分辨推理模型

假设目标位于本舰左舷，本舰转向完成后目标舷角 θ1的最大值、最小值分别为 θL－min、θL－max;目标位于本舰右舷，本舰转向完成后目标舷角θ1的最大值、最小值分别为 θL－min、θL－max。则本舰完成转向后 θ1的取值范围为

将区间［θL－min， θL－max］记为区间 1，［θR－min，θR－max］记为区间 2。

1)区间1和区间2的组合情况分析

如图2所示，理论上区间1和区间2可以有以下七种组合:

根据区间1和区间2的组合情况，实际测得的θ1有两种情况。第1种情况是θ1只落在区间1或区间2中的一个区间;第2种情况是θ1同时落在区间1和区间2，此时，区间1和区间2必然存在重叠区域。这两种情况需要建立不同的判断模型。若为第1种情况，则判断模型如下:

①若区间1和区间2为图2(a)和图2(g)组合，则推断目标左右舷的判断规则为:

如果 θ1∈［θR－min，θR－max］，则目标在右舷;

如果 θ1∈［θL－min，θL－max］，则目标在左舷;

②若区间1和2为图2(b)组合，则推断目标左右舷的判断规则为:

如果 θ1∈［θL－min，θR－min)，则目标在左舷;

图2 区间1和区间2的可能组合

如果 θ1∈ (θL－max，θR－max］，则目标在右舷;

③若区间1和2为图2(c)组合，则推断目标左右舷的判断规则为:

如果 θ1∈［θL－min，θR－min)，则目标在左舷;

如果 θ1∈ (θL－max，θR－max］，则目标在右舷;

④若计算结果为图2(d)组合，则无法推断目标所处舷侧。

⑤若区间1和2为图2(e)组合，则推断目标左右舷的判断规则为:

如果 θ1∈［θR－min，θL－min)，则目标在左舷;

如果 θ1∈ (θR－max，θL－max］，则目标在右舷;

⑥若区间1和2为图2(f)组合，则推断目标左右舷的判断规则为:

如果 θ1∈［θR－min，θL－min)，则目标在左舷;

如果 θ1∈ (θR－max，θL－max］，则目标在右舷。

3)第2种情况的判断模型

第2种情况为θ1落在区间1和区间2的重叠区域，如图3所示。

图3 θ1落在区间1和区间2的重叠区域

此时，令 θL、θR分别为区间 1、2 的中心值，则

假设区间 1、区间2 的重叠区域为［θmin，θmax］。令 U=［θmin，θmax］为论域，L 表示U上的模糊集“贴近θL”，R表示U上的模糊集“贴近θR”。

定义1:当θ1落在区间1和区间2的重叠区域时，模糊集L在θ1处的隶属度为［4］

显然，μL∈［0，1］。当 θ1= θL时，μL=1;当 θ1=θL－min或 θ1= θL－max时，μL=0。

定义2:当θ1落在区间1和区间2的重叠区域时，模糊集R在θ1处的隶属度为

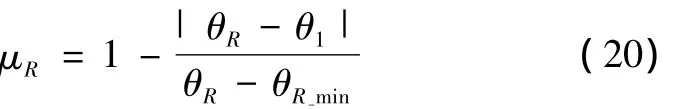
显然，μR∈［0，1］。当 θ1= θR时，μR=1;当 θ1=θR－min或 θ1= θR－max时，μR=0。

显然，θ1越“贴近”θL，目标越有可能位于左舷;θ1越“贴近”θR，目标越有可能位于左舷。当μL＞ μR时，表示θ1与θL更贴近，则有理由推断目标位于左舷的可能性更大。μL与μR相差越大，目标位于左舷的可能性也越大。当 μR= μL时，表示 θ1与 θR、θL的贴近程度相同，则目标位于左舷与位于右舷的可能性相同。当μR＞μL时，表示θ1与θR更接近，则有理由推断目标位于右舷的可能性更大。μR与μL相差越大，目标位于右舷的可能性也越大。当μR= μL时，表示θ1与θR、θL的接近程度相同，则目标位于右舷与位于右舷的可能性是相同的。

定义3:当θ1落在区间1和区间2的重叠区域时，模糊集“更贴近θL”在θ1处的隶属度μL/R为

则μL/R具有以下性质:

① μL/R∈［0，1］;

② μR一定时，μL越大，则 μL/R越大;

③ μL一定时，μR越大，则 μL/R越小;

④ 当 μL=0 时，μL/R=0;当 μR=0 时，μL/R=1。

当μL/R＞ 0.5时，则有μL＞ μR，即θ1“更贴近”θL;当μL/R＜ 0.5时，则有 μL＜ μR，即 θ1“更贴近”θR。根据μL/R的性质，运用μL/R的推断规则如下:

① 若μL/R＞0.5，则目标很可能位于左舷，其概率为μL/R;

② 若μL/R＜0.5，则目标很可能位于右舷，其概率为1－μL/R;

③若μL/R=0.5，则目标位于左舷与位于右舷的概率相等，难以推断目标左右舷。

3 算例验证

假设T0时刻，本舰拖线阵测得目标所处舷角为θ0=82°，根据当时战场态势指挥员决定向左转向分辨目标左右舷。取目标速度Vd=6kn，根据目标舷角分布范围解算模型可得本舰完成转向后的目标舷角分布范围如表1所示。

表1 转向完成后目标舷角的最大值和最小值(°)

若目标初始距离R0=15km，则本舰转向角度α分别为6°、7°、8°时，转向完成后的目标舷角区间1和区间2均不重叠。根据本舰转向完成后实际测得的舷角θ1，采用第一种情况的判断模型即可分辨目标左右舷。例如，若本舰向右转向角度 α=6°，实测得到 θ1=97.4°，则有 θ1∈［θL－min，θL－max］，目标位于本舰左舷;若实测得到 θ1=88.7°，则有 θ1∈［θR－min，θR－max］，目标位于本舰右舷。

若目标初始距离R0=10km，则本舰转向角度α分别5°、6°时，转向完成后的目标舷角区间1和区间2重叠。若实际测得的目标舷角θ1没有落在区间1和区间2的重叠区域，则采用第1种情况的判断模型即可。例如，若本舰向右转向角度α=5°，实测得到θ1=103.4°，则有 θ1∈［θL－min，θL－max］且 θ1∉［θR－min，θR－max］，因此，目标位于本舰左舷;若实测得到 θ1=94.7°，则有 θ1∈［θR－min，θR－max］且 θ1∉ ［θL－min，θL－max］，目标位于本舰右舷。

若实测得到θ1落在区间1和区间2的重叠区域，例如θ1=97.8，显然，θ1∈ ［θR－min，θR－max］且 θ1∈ ［θL－min，θL－max］，此时，应采用第2 种情况的判断模型，通过计算式(21)的值进行判断。由表1 得，θL－min=96.7，θL－max=109.5，θR－min=86.8，θR－max=100，根据式(17) ～式(21)计算得 θL=103.1，θR=93.4，μL=0.1719，μR=0.2787，μL/R=0.3815，μL/R＜ 0.5，因此，目标位于右舷的可能性大，其概率为61.85%。