基于微分对策的潜艇鱼雷攻击占位问题研究*

2013-11-09孙华春

指挥控制与仿真 2013年3期

张会，吴鹏，孙华春

(海军潜艇学院，山东青岛 266071)

1 潜艇鱼雷攻击可占位条件分析的微分对策模型

成功占领攻击阵位是潜艇对目标实施鱼雷攻击的前提条件。假设潜艇P预对定速定向机动的目标E进行鱼雷攻击占位，ve为目标E的速度，vp为P的速度，vy为鱼雷速度。攻击阵位域为以目标前方距离ved/vy的点O为圆心的圆形区域［1-5］，称为攻击阵位圆，称点O为命中点。为简化推导，将潜艇鱼雷攻击占位问题看成针对命中点O的追逃问题，并称O为影子目标。以O为原点，目标运动方向为x轴正向，x轴正向顺时针旋转90°为y轴正向，建立坐标系，潜艇相对于影子目标的运动方程为

其中，函数u(t)为x轴到潜艇运动方向角，顺时针为正。占位成功条件，即目标集合表示为

根据定性微分对策理论和方法［5，6］，可推导潜艇能成功占位的条件。构造汉密尔顿函数:

其中，γ→=(γ1，γ2)T。

令

同时，让

得到潜艇的最优策略:

对应的汉密尔顿函数值为

将目标集边界x2+y2=d2表示成参数形式:

其中，s为与x轴正向夹角，~t为发现目标时刻。目标集边界指向决策空间的单位法向量为

将式(5)代入式(3)，得到E的最优策略在目标集边界上的值为

对应的汉密尔顿函数值为

由式(7)可知，当vp≥ve时，H(x*，y*，u*，γ)恒大于零，故整个决策空间都是可占位区域。当vp＜ve时，存在不可占位区域。首先考虑上半平面，即0≤s≤π对应部分。记s0=arccos(-vp/ve)，则目标集边界上的点对应于0≤s≤s0的所有点为UP，而对应于s0的点为BUP。以s0对应的点为起点构造界栅，伴随方程和初始条件为

得

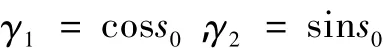
倒向状态方程及其初始条件为

得

其中，τ=~t-t。

对式(10)消元可得界栅表达式:

再考虑下半平面，记s0=-arccos(-ve/vp)，可得以s0对应点为起点的界栅表达式

根据式(11)和式(12)可绘制出潜艇可占位区域如图1所示。图1中α=arcsin(vp/ve)，直线QAM、直线QBN的方向角分别为 ±α，故|QO|=ved/vp。射线AM、射线BN和沿逆时针的圆弧AB，所围成的圆外非封闭区域为可占位区域。

由前述分析可知，给定占位速度条件下，潜艇最佳占位机动方案为匀速定向机动。后面用目标运动方向到潜艇占位机动方向角(顺时针为正)q表示占位方案，并称其为占位方向角。

图1 鱼雷攻击可占位区域图

2 可占位情形下的占位方案优化

当潜艇可成功占位时，为尽快实施攻击，应尽量缩短占位时间。以式(1)为约束条件，式(2)为目标集，取目标函数为

建立占位方案优化微分对策模型，称所求得的最优方案为最短时间占位方案。其中，tf为占位过程结束时间。根据定量微分对策和最优控制理论对最优占位方案进行分析［6，7］，可得潜艇最优策略 u*为

可知，最短时间占位方案的机动方向与潜艇到达攻击阵位圆时潜艇位置点到命中点的向量方向一致。潜艇最优占位方向和相对于影子目标的运动如图2所示。图2中，O为命中点，M为潜艇开始占位时的位置点;D为影子目标距离(潜艇到命中点的距离);φ为影最短时间占位方案速度向量。|TP|=vp，其相对运动由ΔSON相似于ΔPTM，可依次得到:

式中，vx和Dx分别表示最佳占位方案对应的相对运动速度和相对运动航程。

图2 最短时间占位方案计算方法示意图

3 仿真验证

取 D=10nmle，φ =arctan(d/D)+ π/10，Vp=10节，Ve=18 节，Vy=45kn，d=5nmle。由前述可占位条件可判定，潜艇可以实现成功占位。取一个足够长时间tmax，对潜艇采用不同占位方向角q进行机动的过程分别进行仿真，仿真结束当且仅当潜艇占领攻击阵位或仿真时间到达tmax，即仿真结束时间:

绘制出q和tend关系曲线如图3所示。图3中，横坐标为q，纵坐标为tend，“*”号表示的点为用式(17)和式(18)计算出的点(q，tf)。

4 结束语

本文使用微分对策理论对潜艇鱼雷攻击占位问题进行研究。与初等数学方法相比，使用微分对策理论对鱼雷攻击占位问题进行研究的意义主要有两点:1)没有首先将潜艇的规避机动限定为直线运动，而是假设潜艇可以以任意方式机动，通过理论分析证明在给定规避速度大小的条件下，潜艇的最佳规避策略为直线运动;2)给出了给定占位速度大小条件下潜艇最短时间占位方案的解析计算公式，在进行此公式推导时使用了潜艇最佳机动策略的有关结论，目前还未见到使用初等数学方法完成此公式推导的文献。