超声速钝锥三维分离条件的数值分析

李 沁，张涵信

（1.中国空气动力研究与发展中心，四川绵阳 621000；2.北京航空航天大学国家计算流体力学实验室，北京 100083）

0 引 言

分离和旋涡是常见的流动现象。对于二维分离，流场通常会出现逆压梯度，并产生分离旋涡等流动结构；三维分离则复杂得多，首先会存在不同的分离类型，如开式分离与闭式分离；与此相联系，分离起始会出现不同的奇点形态，如正常点起始、鞍点起始以及鞍结点组合起始；旋涡的涡轴既可以与来流垂直（与二维情况接近），也可能与来流平行。在实际问题中，在一定迎角下的机翼分离、二维拐角／台阶分离都属于二维情况下的分离，逆压梯度引起的压力增加对流体力学特性尤其是气动性能产生重要影响；而三维分离产生的旋涡，既可能增加升力——如流向涡产生的涡吸力，又可能由于分离流态的变化，引起气动性能的降低，如涡轴抬升以及涡破裂。因此，准确预测分离，开展分离发生、发展的理论研究，具有重要的实际意义。其中分离理论的研究成果，可以直接用于计算结果的检验和分析；同时当前数值计算所采用的边界条件，由于在分离点附近理论上不严格、数值上存在误差，往往造成计算得到的分离与实验存在较大差距，从而影响气动特性的准确计算；分离理论研究将有助于这些难题的解决。

不可压二维分离的理论由Prandtl［1］给出，其标志是Prandtl分离条件，该条件既被用在定常也被用在非定常的表面分离；对于更为复杂的物面外分离，Moor、Rott和Sears提出 MRS准则［2］。张涵信院士对此也作了研究并得到更为一般的形式［3］。三维定常分离的研究学者主要有Hesieh、K Wang、Tobak和Peake等，其中关于分离线性质的研究曾经存在长时间的争论，最后由张涵信院士给出的结果平息了学术争论［3－6］，更为重要的是研究还给出了分离判则。在文献［7］中，张涵信院士给出了关于流动分离详细和完整的理论。

最近张涵信院士［8］通过将非定常流动中密度影响吸收转换为一个类似速度梯度项，从而利用定常分离的研究成果来阐述非定常分离。比较非定常分离判则和定常分离判则，可以发现非定常分离的前三个条件实际上与定常分离是一致的，所以深入开展定常分离的数值分析仍然具有必要性。

关于如何开展三维定常分离理论的数值分析，目前有两个技术性问题：第一个是三维分离判则给出的结论基于分离坐标系，三个坐标轴分别是分离线、分离线法向和物面法向，而实际计算曲线坐标系除个别简单情况外，坐标系与分离坐标系之间缺乏直接联系，对分离判则进行计算分析与验证较为困难；第二个是密度的影响问题，密度在高马赫数下的分离判则中所起作用需要深入开展研究。

本文的研究正是基于这样的考虑，开展了15°半锥角钝锥超声速层流分离条件的数值研究。来流马赫数为1.8和10.6，迎角从10°到40°。研究一方面探索分离条件的数值分析方法，给出分析的结果并与理论进行比较；另一方面也研究不同马赫数对分离形态的影响，并给出不同情况下流动的具体分离特征。

在第1节，首先介绍数值模拟使用的方法并给出验证算例；在第2节给出三维数值分离判则的数值分析方法；应用数值分析方法，在第3节中对超声速钝锥计算结果进行了分析，对各种条件下分离特征进行了研究；最后在第4节给出研究结论。

1 数值方法

1.1 计算方法

数值模拟控制方程为守恒型的积分Navier－Stokes方程：

其中U是守恒变量向量，F是控制体边界上的通量向量。V和S是控制体的体积和边界面面积是S的法向单位向量。采用通常基于六面体的有限体积方法进行离散，控制方程可表示为：

式中，V代表网格单位的体积，F、Fv、S分别代表网格边界面上的无粘、粘性通量和面积向量；由于所采用方法为标准有限体积算法，文中将不对这些变量作详细解释。进一步，有限体积求解采用格心法，即流动参数控制点取在控制体中心，单元边界面上的流动参量需要插值格式得到。对于无粘通量，其计算方法采用MUSCL格式，具体形式为：

其中，κ和b是格式调节因子，1≤b≤，κ为时格式为三阶精度；通量F（UL，UR）采用了耗散小的有限差分裂Roe格式。粘性通量采用中心差分进行计算。时间算法部分，由于求解问题为定常问题，采用LU－SGS隐式进行迭代求解。

物面速度边界条件为无滑移条件，在M＝1.8情况下，温度边界条件为绝热壁条件；在M＝10.6情况下，为等温壁条件，壁面温度为294.44K。外边界为无反射边界条件。

1.2 数值验证

由于本文所选取的钝锥外形，国外曾经在M＝10.6、迎角为20°时开展过验证实验（Cleary［9］），本文也针对该状态进行验证计算，其目的是通过考察程序对CFD的难点——热流的计算准确性来开展程序验证。该算例Re数为1.1×105，流动为层流，计算条件详见3.1节。

图1给出了用驻点热流归一化后的热流分布及其与实验结果比较，其中φ＝0°子午线为背风区物面对称线。比较显示计算与实验符合良好。

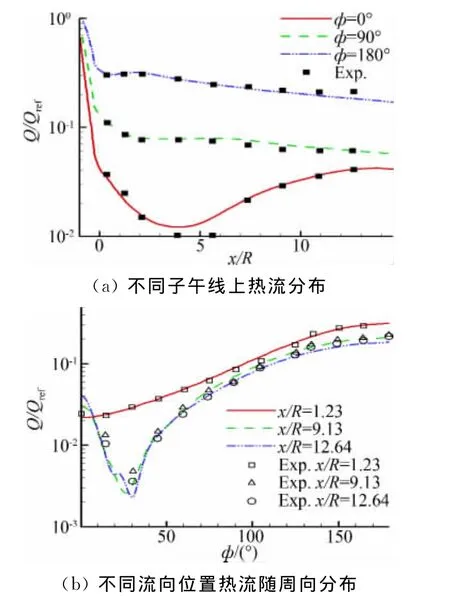
图1 计算热流与Cleary实验［9］比较Fig.1 The comparison of heat flux between the computation and Cleary’s experiment［9］

验证结果表明，计算具有较高的数值模拟精度，可以用来开展进一步的钝锥分离研究。

2 三维分离判则的数值分析

虽然在文献［3－7］中，张涵信院士早就给出了三维定常分离的判则，但由于分析是在分离坐标系下进行，所以除了一些十分规则的几何外形外（如方腔），分离判则的直接数值分析存在一定困难。本节拟通过对分离判则开展分析，得到不依赖于具体坐标系的、易于数值验证的形式。

图2给出了理论分析所用的曲线坐标系，其中y轴沿分离线，轴正方向为分离线流向，x轴为与y轴垂直的物面曲线，z轴为与x、y正交的曲线坐标；速度u、v、w分别与x、y、z轴对应。值得注意的是，z轴通常并不位于分离流面。再附理论分析所用坐标系与之类似。

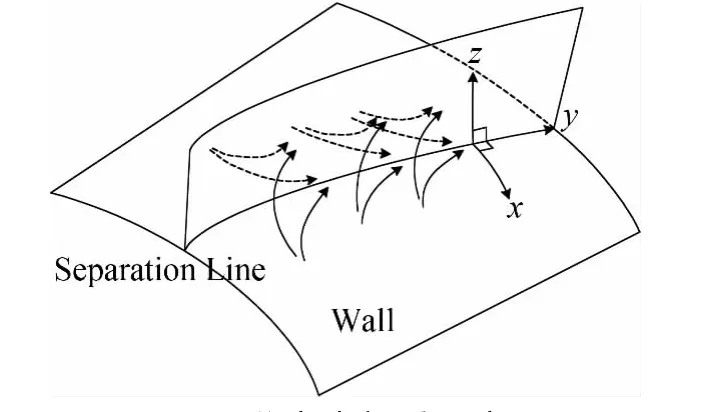
图2 分离坐标系示意图Fig.2 The schematic of the coordinate system of the separation

文献［3－7］给出的三维定常分离条件为：流动在物面分离线上满足

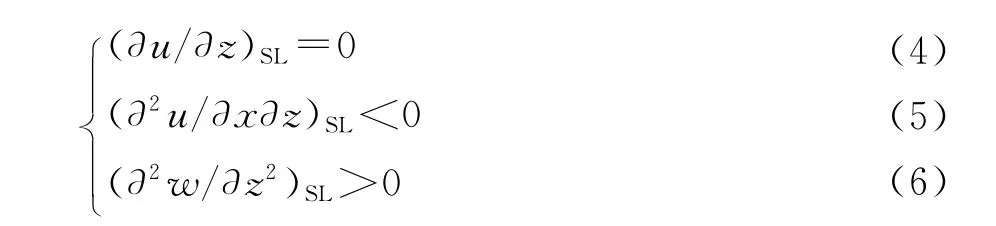
其中下标“SL”表示分离线。

与之对应，三维定常再附条件为：流动在物面再附线上满足

其中下标“AL”表示再附线。通常计算中观察到的是第一类再附（（∂2u／∂x∂z）AL＞0）。

从式（4）～式（9）可以看出，分离和再附条件的关键变量是：∂u／∂z、∂2u／∂x∂z和∂2w／∂z2。下面分别对这些变量与式（4）～（9）中的基本关系进行分析，讨论分离判则在一般计算坐标系下的数值分析方法。

2.1 ∂u／∂z＝0

为了能够脱离具体的分离坐标系，考虑到分离坐标系下速度矢量的正交性，首先补充v、w的速度梯度组成正交的空间矢量：（∂u／∂n，∂v／∂n，∂w／∂n）＝∂V／∂n。如果去掉矢量的法向部分，则可得到∂V／∂n在物面切平面上的投影。“∂u／∂z＝0”表示投影矢量在分离线上将与该线相切。为此考虑位于物面切平面的新矢量：ℑ＝∂V／∂n－n（n·∂V／∂n），分离条件（4）意味在分离线上ℑ与之相切；新矢量脱离具体的坐标表达，可以方便在计算坐标系下计算。

2.2 ∂2u／∂x∂z＞0与∂2u／∂x∂z＜0

考虑式（4）或式（7），如果面向分离坐标系y轴的正方向，∂2u／∂x∂z＜0意味着在y轴两侧ℑ有指向y轴的分量。这样考虑2.1节的分析，如果在分离线附近以ℑ为“速度场”画表面流线，则流线将向分离线汇聚，所画出的极限流线或包络线应该与分离线重合。这个结论可以用来数值验证前两个分离条件的正确性。实际上ℑ对应表面摩擦力确定的矢量场［7］，所以如果分离线由速度场确定的极限流线给出，分离条件式（4）、式（5）也表述为：极限流线与摩擦力线给出的分离线相同。类似地，对于与∂2u／∂x∂z＜0条件对应的再附线，可知用矢量场ℑ画出的表面流线将由分离线向两侧发散，再附线是ℑ矢量场的不稳定轨线。

2.3 ∂2 w／∂z2

类似地，考虑矢量（∂2V／∂n2）w＝（∂2u／∂n2，∂2v／∂n2，∂2w／∂n2）w，其中∂／∂n表示物面法向的方向导数、“w”表示物面，则分离坐标系下的∂2w／∂z2可表示为：n·∂2V／∂n2，该式脱离具体坐标表达，可由数值计算结果方便地得到。具体地，根据n·∂2V／∂n2大于零或小于零将物面进行“二值化”着色，通过考察分离线和再附线所在区域开展与理论的对比分析。

3 钝锥三维分离条件的数值分析

3.1 计算条件与网格生成

计算外形为15°钝锥，头部半径为1，球心到底部长15。网格为含奇性轴的旋成体网格。具体计算条件见表1。

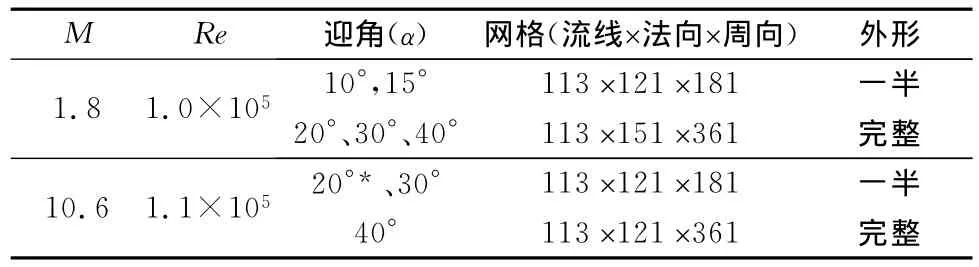
表1 计算条件与网格Table 1 The condition of computation and grids

其中“＊”表示该状态同时用于1.2中的验证计算。

3.2 钝锥M＝1.8、Re＝1×105下系列迎角分离拓扑

以下将分三方面对该条件下的钝锥分离进行分析。其中在图例中，“S”或“SP”表示鞍点，“N”表示结点，“SL”表示分离线，“AL”表示再附线。

3.2.1 基本分离特性

对于旋成体有迎角表面分离形态，可以根据两个基本特征进行分类：分离类型和多次分离的级数。图3给出了不同迎角下极限流线表示的流动表面分离。结果显示，钝锥分离由两个基本组成部分构成：头部分离和锥体分离。

（1）头部分离。在球锥头部，起始分离类型为闭式分离；分离由对称子午线上的鞍点开始，结束于结点（螺旋点、正常或退化结点）。其中10°迎角为背风区分离刚刚开始的情况（图3a），头部分离由位于对称子午线上的结点开始，通过鞍、结分叉，发展出“鞍点→分离线→结点”结构的典型闭式分离形态。随着迎角的增大，头部分离发展出更加复杂的形态（将在下面讨论），起始分离鞍点不在对称子午线上，流动不对称，但闭式分离的基本特征仍然保持。

（2）锥体分离。由于锥体分离随迎角的增大会出现多次分离，所以锥体分离仅讨论最外侧的主分离。锥体主分离类型在15°、20°和30°为正常点起始的开式分离；当迎角增大到40°时，锥体主分离发生鞍结点分叉，分离线分裂成两部分，第一部分一侧仍为由正常点起始的开式分离，另一侧则由鞍点起始，分离在退化结点结束；第二部分由同一鞍点起始，分离线移植延伸到钝锥地面，如图3（d）所示。

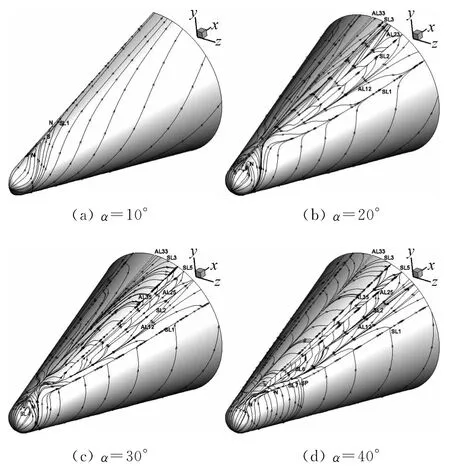
图3 系列迎角下速度极限流线给出的表面分离拓扑Fig.3 The surface separation topology by limiting streamlines at series of angles of attack（α）

从表面流线看，锥体的多次分离由10°迎角的主分离出现开始，逐渐发展出两个二次以上分离（20°下的SL2和SL3），进一步发展出三个二次以上分离（20°下的SL2、SL3和SL5），复杂程度不断增加，但是新出现的多次分离都呈近似直线分布，体现类锥形流特征。

3.2.2 分离线的奇点分布规律

文献［7］给出分离线上奇点分布规律：分离线上若存在奇点，则为交替分布的鞍点和结点；若分离由奇点开始，则奇点为鞍点；若分离线进入奇点结束，则奇点为结点。下面以钝锥头部分离线上奇点分布为例，对分布规律开展数值对比分析。

图4显示的10°迎角背风区表面极限流线给出了十分少见的、分离刚开始的结构。头部流线拓扑由鞍点开始，结束于对称子午线上的稳定结点；鞍点上方、对称子午线上存在不稳定的结点；鞍点向上的奇轴构成一段很小的分离线。鞍点和结点通过鞍点的奇轴连接。

图4 10°迎角头部表面分离的奇点分布Fig.4 The singular－point distribution of the surface separation atα＝10°

随着迎角的增大，在一定范围头部分离线奇点逐渐形成稳定的拓扑结构，该结构以迎角20°状态为代表，如图5所示。图中头部分离线分别起始于对称子午线上方两侧和下方线上的两个鞍点，结束于螺旋点。在分离线上，鞍、结点交替分布。进一步的分析（见3.2.3节）倾向于认为对称子午线两侧、向下延伸的收敛曲线是第二类再附线［7］，计算显示该曲线的演化是与分离线结合。值得提出的是，上、下鞍点的奇轴并没有直接连接，因此不违背结构稳定性的要求。当迎角增大到40°时（图6），头部表面分离变得非常复杂，出现两个主控的不稳定节点，但仍然可以通过鞍点的奇轴将奇点连接起来，在连接线上，鞍、结点交替分布；同时底部的分离线仍由鞍点开始，结束于退化的结点；左右两侧分离结构相似但不对称，尤其是，底部分离线上、原来在对称子午线上的鞍点已移动到头部右侧。

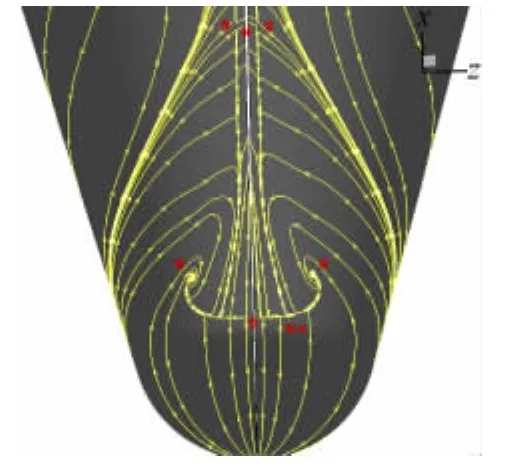
图5 20°迎角头部表面分离的奇点分布Fig.5 The singular－point distribution of the surface separation atα＝20°

图6 40°迎角头部表面分离的奇点分布Fig.6 The singular－point distribution of the surface separation atα＝40°

通过数值分析表明，分离线上的奇点符合文献［7］给出的拓扑规律。

3.2.3 分离、再附判则的数值分析

由分析可知，如果分离线和再附线用计算给出的速度极限流线表示（图7中用黄色线条显示），则式（4）、（5）、（7）和（8）表明它们应该与由矢量场ℑ给出的分离和再附线（图7中用黑色线条显示）重合。在这样的思路下，我们将后者作为背景，将速度极限流线给出的分离、再附图像叠加在背景上来进行比较。图7以40°迎角为代表，给出了比较结果。结果表明，矢量场ℑ给出的分离和再附线与速度极限流线得到的结构几乎完全重合：黄色线条完全覆盖黑色线条，这表明计算与分离条件式（4）、（5）和再附条件式（7）、（9）相符，彼此得到相互印证。

关于条件式（5）和（9），可以利用数值结果直接计算n·∂2V／∂n2，并在物面用红色显示大于零的区域、用灰色显示小于零的区域，得到结果以30°迎角为代表，如图8所示。在头部区域，闭式分离的分离线始终处于n·∂2V／∂n2大于零区域，对称子午线两侧、向下延伸的收敛曲线由于在靠近头部位置位于小于零区域，分析倾向认为该线是第二类再附线；主分离线始终位于n·∂2V／∂n2大于零区域，二次以上分离线也基本位于大于零区域——有时该区域仅表现为一条窄缝，而分离线恰好从中间穿过；锥体部分的再附线，基本位于n·∂2V／∂n2小于零区域，说明流场中再附线主要为第一类再附线。计算结果与理论分析基本上是一致的。

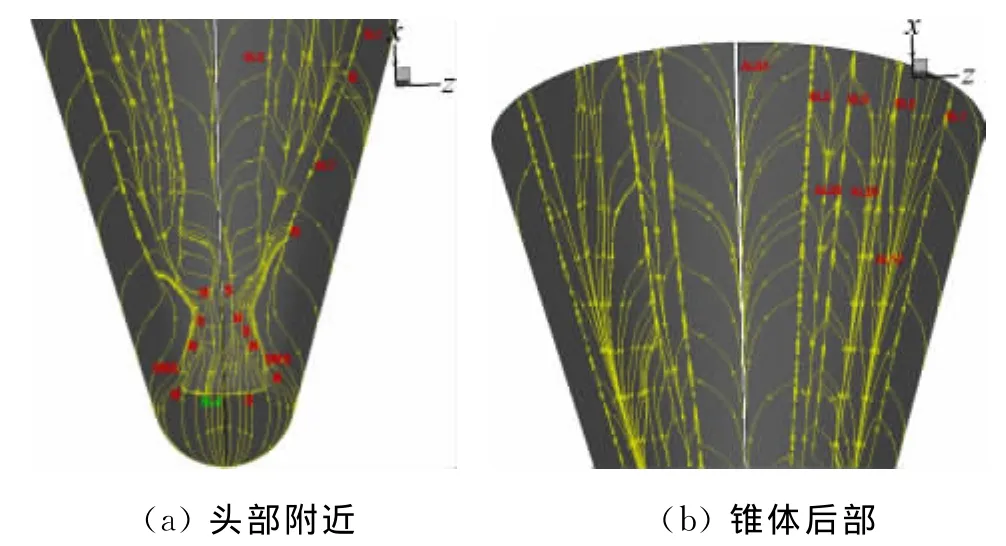
图7 40°迎角物面速度极限流线与ℑ流线叠加Fig.7 The superimposition of the surface limiting streamlines and that given byℑatα＝40°

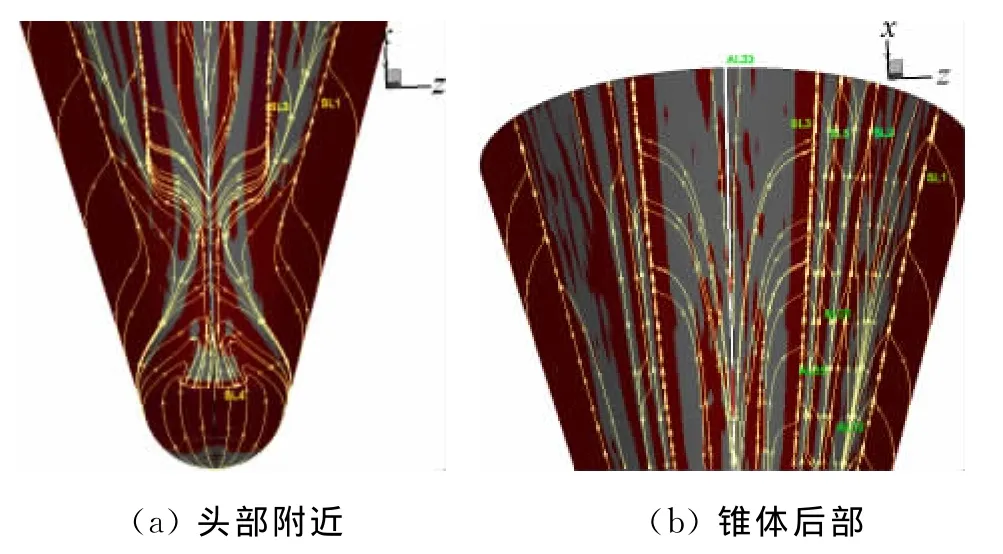
图8 30°迎角物面n·∂2V ／∂n2 分布Fig.8 The surface distribution of n·∂2V ／∂n2 atα＝30°

3.3 钝锥M＝10.6、Re＝1.1×105下系列迎角分离拓扑

分两方面对该条件下钝锥分离进行分析。

3.3.1 基本分离特性

图9、图10表明，在高超M＝10.6、Re＝1.1×105来流条件下，所计算迎角钝锥背风区都出现分离。基本分离形态是由正常点起始的开式分离；从20°左右迎角起，流动在背风区出现二次分离，随迎角增大，主分离和二次分离起始位置向头部移动，分离区域不断扩大；分离线、再附线交替分布，将物面分割成不同区域。值得指出的是，当迎角为40°时，再附线AL12在锥体后部逐渐出现与分离线SL2融合的趋势，而分离线SL2仅在靠对称面一侧流线向其汇聚（即满足式（5）），另一侧则显示发散的特征（即分离坐标系下：（∂2u／∂x∂z）＞0），这种现象的数学物理规律尚需进一步分析。总的来说，高超情况下钝锥大迎角分离拓扑形态明显比M＝1.8下简单。

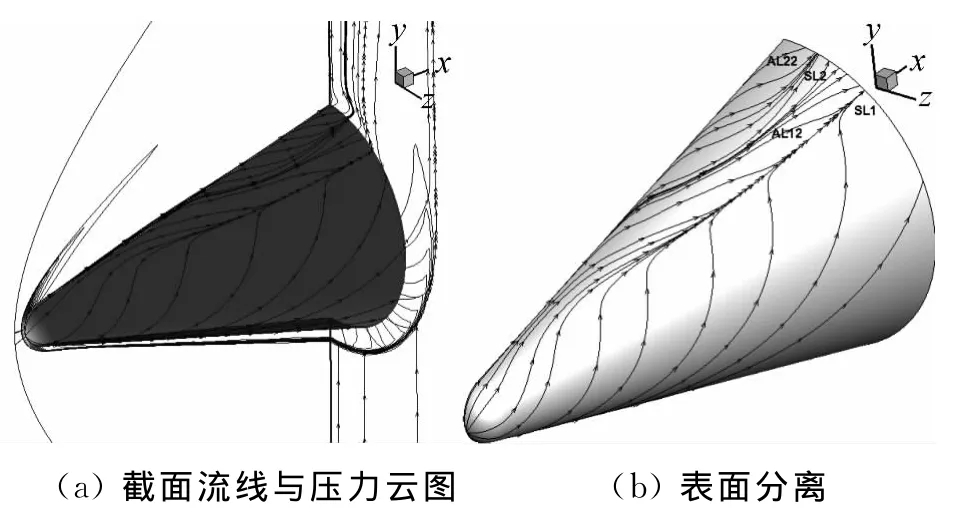
图9 迎角20°的验证计算与表面速度极限流线Fig.9 The validating computation atα＝20°and the surface limiting streamlines

图10 迎角30°、40°的表面速度极限流线Fig.10 The surface limiting streamlines atα＝30°and 40°

3.3.2 分离、再附判则的数值分析

类似地，为了考察分离判则式（4）、（5）和再附判则式（7）、（8），我们将由速度极限流线得到的分离线、再附线与由矢量场ℑ给出的结构叠加，结果显示在图11。结果同样表明，矢量场ℑ给出的分离和再附线与速度极限流线得到的结构几乎完全重合，从而在数值上验证上述条件。

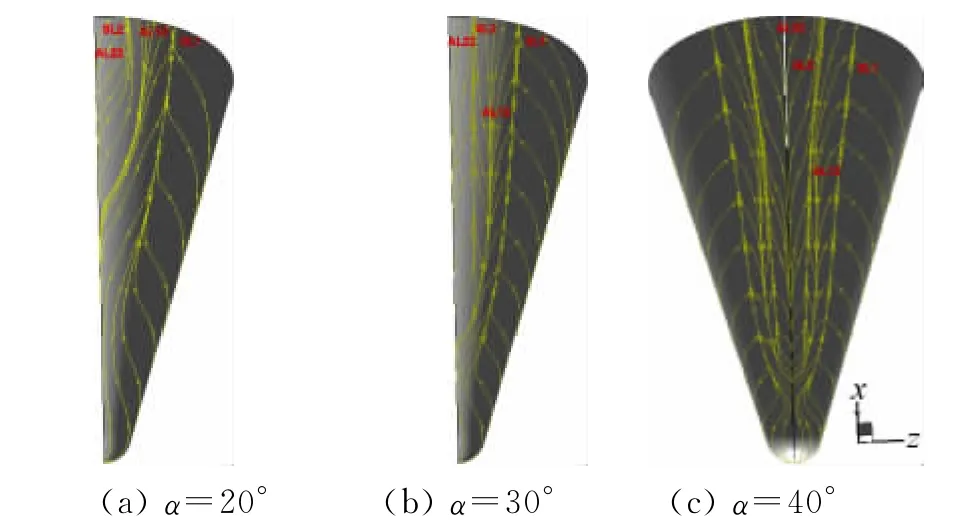
图11 钝锥物面速度极限流线与ℑ流线叠加Fig.11 The superimposition of the surface limiting streamlines and that given byℑof the blunt cone

但当利用数值结果直接计算n·∂2V／∂n2来验证分离、再附条件式（6）、（9）时，却发现n·∂2V／∂n2大于零、小于零的区域分布散乱，没有明显规律性，缺乏M＝1.8情况下分离线、再附线与不同区域间明显存在的规律性。这方面的原因可能源于n·∂2V／∂n2与式（6）、（9）尚存在误差，或者由于高马赫数下密度引起的可压缩效应，针对该问题的进一步分析正在进行中。

4 结 论

本文采用数值模拟的手段，对不同马赫数、系列迎角下的钝锥分离拓扑进行了研究，其目的是探讨分离判则的数值分析方法并开展相应分析。计算经过验证，结果准确可靠，可以用来提供数据以开展分析研究。经过计算、分析，有以下结论：

（1）文中通过数值模拟，详细给出了普通超声速和高超范围钝锥系列迎角下的分离特性。结果表明，在来流M＝1.8条件下，流动分离模式由头部闭式分离和锥体开式分离组成，锥体分离随迎角增大会进一步出现多次分离；在来流M＝10.6条件下，在计算迎角下分离模式仅有开式分离；

（2）文中通过分析文献［7］中分离、再附判则，构造了不依赖于具体坐标的矢量ℑ和n·∂2V／∂n2，给出了判则的等价表述。新的表述可以利用数值模拟结果进行直接计算，更加有利于数值分析；

（3）文中基于数值模拟结果和构造的矢量，对分离、再附判则进行了数值分析，结果表明当M＝1.8时，计算与理论一致；当M＝10.6时，数值分析与分离判则式（4）、（5）和再附判则式（7）、（8）一致；

（4）对于来流M＝1.8的情况，钝锥头部会出现复杂的鞍、结点组合。虽然这些奇点拓扑结构复杂，但其沿分离线等的分布符合文献［7］中给出的拓扑规律。

［1］PRANDTL.Über Flüssigkeitsbewegung bei sehr kleineir Reibung［M］／／Verh.III，Int.Math.Kongr.Heidelberg，1904：485－491.

［2］MOORE F K.Boundary layer research［M］.GORTTER H G，Edited.Berting，Springer Vertag，1958：296－310.

［3］张涵信.二维粘性不可压缩流动的通用分离判据［J］.力学学报，1983，6：559－570.

［4］张涵信.三维定常粘性流动的分离条件及分离线附近流动的性状［J］.空气动力学学报，1985，1：1－12.

［5］张涵信.分离流的某些进展［J］.航空学报，1985，6（4）：301－312.

［6］ZHANG H X.Numerical simulation of three dimensional separated flow field and application of topological theory［J］.AdvancesinScienceofChina，Mechanics，1991，1：59－80.

［7］张涵信.分离流与涡运动的结构分析［M］.国防工业出版社，2005.

［8］张涵信，张树海，田浩，等.三维可压缩非定常流的壁面分离判据及其分离线附近的流动形态［J］.空气动力学学报，2012，30（4）：421－430.

［9］CLEARY J W.Effects of angle of attack and bluntness on laminar heating－rate distributions of a 15°cone at a Mach number of 10.6［R］.NASA TN D－5450，1969.