逆流推力矢量喷管主流附体及控制方法研究
2013-11-09史经纬王占学张晓博刘增文
史经纬,王占学,张晓博,刘增文
(西北工业大学 动力与能源学院,陕西 西安 710072)
0 引 言
作为固定几何气动矢量喷管的一种主要形式,逆流推力矢量喷管结合了气动式矢量喷管的结构简单和机械式矢量喷管的连续控制等优点[1-3],与其它几种气动控制形式矢量喷管[4-7],如激波矢量控制SVC(Shock Vectoring Controlling)、喉部偏移TS(Throat Shifting)等相比,逆流推力矢量喷管有着推力损失小、二次流需求少、不需高压二次流及推力矢量效率高等明显优点[1],因而成为未来高推重比航空发动机排气系统重点关注的方案之一。
国外对逆流推力矢量喷管的研究始于20世纪90年代,Strykowski等人率先开展了基于二元收-扩构型的逆流推力矢量喷管的地面静态冷、热态缩比模型试验与数值模拟,研究了气动、几何参数对逆流推力矢量喷管特性的影响及控制系统实现方法[8-11],随后NASA Langley研究中心Hunter等人在前者缩比模型的基础上完成了放大尺寸的模型试验,并对来流Ma数的影响进行了数值模拟[12-13]。国内对此方面的研究主要是采用数值模拟技术研究逆流推力矢量喷管参数影响规律及非定常特性。南京航空航天大学汪明生等人[14]研究了逆流推力矢量技术的非定常现象、真空源等核心问题,北京航空航天大学邹欣华等人[15]数值模拟了马赫数对逆流推力矢量喷管性能的影响。尽管前人的研究已经揭示了气动几何参数影响规律,非定常现象,提出了真空源方案;然而,主流附体作为限制逆流推力矢量喷管应用的一个主要瓶颈,国内外研究人员对其的流动现象与控制方法的研究仍不多见,因此有必要进行基础的研究分析。
本文主要从逆流推力矢量喷管主流附体的角度出发,采用数值模拟方法研究主流附体产生的机理、参数变化规律,并验证了提高抽吸压力和增大喷管主流压比实现附体主流脱体的控制方法。
1 数值计算方法
1.1 模型介绍
逆流推力矢量喷管几何结构如图1。在二元收-扩喷管外对称加装了两个外罩,与基本喷管形成上、下二次流通道。需要矢量推力时,改变一个通道的边界条件(如变为抽吸条件),形成主流两侧压力不对称分布,控制主流偏转,实现推力矢量。逆流推力矢量喷管的主要参数包括:基本喷管A9/A8=1.69,出口高度H=4cm,外罩长度L=7H,外罩横向宽度C=1.875H,次流通道高度G=0.5H,外罩唇口切线角度θ=30°。

图1 逆流推力矢量喷管几何结构Fig.1 Geometric model
1.2 计算格式及计算网格
采用时间推进有限体积法,基于密度和速度耦合算法求解守恒型N-S方程。对流项、湍动能项及湍动能耗散型运用空间二阶迎风离散格式,粘性项为空间二阶中心差分格式。湍流模型选用RNG理论修正的k-ε模型,壁面处理选用增强型壁面函数。
计算网格如图2,采用结构化分区生成,并对壁面以及剪切层出分别进行了加密处理,保证壁面y+不超过3。
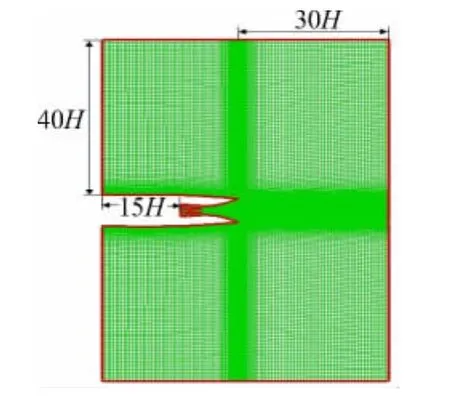
图2 计算网格Fig.2 Computational grid
1.3 边界条件
基本边界条件及参数如下:喷管自由来流总压=101.50kPa,总温=300K,来流为水平方向;远场边界自由来流Ma∞=0.05,P∞=101.32kPa,T∞=300K;出口压力Pe=101.32kPa,出口总温=300K;抽吸侧给定出口静压P2=50.66kPa,T2=300K;喷管进口总压=792.77kPa,总温=300K;同向侧流动给定气流进口总温、总压,=101.32kPa,=300K。壁面选用绝热无滑移边界条件。
2 主流附体形成机理及特征
逆流推力矢量喷管工作时,由于上下次流通道的二次流气动参数不同,造成主流上、下两侧压力不对称,使得喷管主流发生偏转,如图3所示。主流下侧压力分布基本与周围大气压力持平,上侧压力分布受到抽吸压力、主流卷吸以及逆流剪切层的影响。抽吸与卷吸作用造成主次流交汇处形成低压区,周围大气被吸入外罩,并与主流形成逆流剪切层。
二次流通道抽吸压力越小,主次流交汇处压力越低,逆流对主流的反向牵引力越大,主流偏转角度越大,即推力矢量角越大。当主流偏转到到一个临界角度时,主流足够靠近外罩壁面,此时再进一步减小二次流抽吸压力,将会造成主流偏转角度急剧增加,主流贴附到外罩内壁面,并沿着外罩方向流动,即形成所谓的主流附体现象,亦即Conda效应。
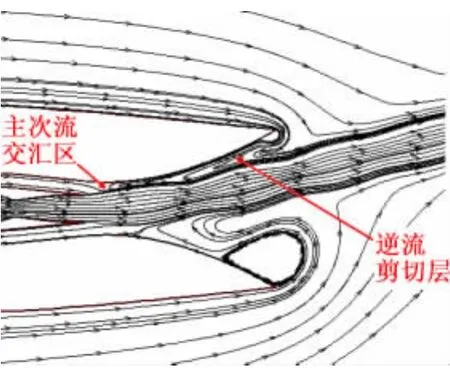
图3 逆流推力矢量喷管流线图Fig.3 Streamline of counter-flow thrust vectoring nozzle
图4给出了二次流抽吸压力逐渐降低的过程中推力矢量角的变化规律。抽吸压力与大气压力比值分别为:0.80、0.75、0.70、0.65、0.64、0.63、0.62、0.61、0.60、0.55、0.45、0.40,其它气动参数取基本参数(如1.3节)。从图中可以看出抽压力比由0.61降低至0.60时,推力矢量角骤然上升(由17.1°升至32°),主流出现附体现象,此时则定义0.61为临界抽吸压比。当主流附体后,随着抽吸压力的继续减小,推力矢量角基本不再变化。因此,逆流推力矢量喷管出现主流附体时存在临界抽吸压力。
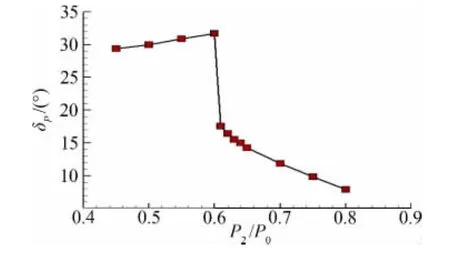
图4 推力矢量角随抽吸压力的变化Fig.4 Thrust vectot angle vs suction pressure
3 主流附体退出方式研究
对二维逆流推力矢量喷管,在地面静态推力工况下,采用控制体积法(如图5)分析得出矢量偏转角度与喷管气动、几何参数的关联关系如下;
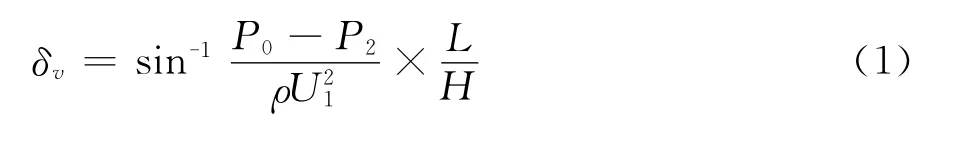
其中下标0代表周围大气,1截面代表喷管出口,2截面代表抽吸侧进口,3截面代表同向侧出口。从式(1)可以看出,对于固定几何气动矢量喷管,增加喷管落压比(即提高主流动量)或增大二次流抽吸压力均可使主流偏转程度减小,亦即增加喷管落压比或增大二次流抽吸压力,均可能实现附体主流脱体。
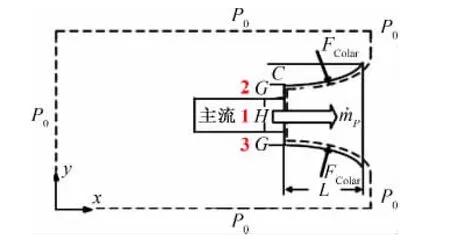
图5 控制体积示意图Fig.5 Control volume sketch map
3.1 提高抽吸压力实现附体主流脱体
保持其它气动参数为基本参数,取抽吸压力与周围大气压力之比分别为0.50、0.55、0.60、0.65、0.66、0.67、0.68、0.70、0.75、0.80逐渐增大。图6对比了二次流抽吸压力从大到小逐渐降低时与二次流抽吸压力从小到大逐渐增加时推力矢量的变化。可以看出,只有当二次流抽吸压力比增加至0.66时(如图7),主流才从外罩内壁面脱体,而不是想象的当二次流抽吸压力比增加到0.61时,主流就从外罩内壁面脱体,即主流从外罩内壁面脱体存在明显的迟滞效应。主流脱体的临界压力点为65.86kPa,该值大于主流附体的临界压力点(60.68kPa)。随着二次流抽吸压比继续增加,推力矢量角随抽吸压力的变化规律与二次流抽吸压力逐渐降低时推力矢量角与抽吸压比的变化规律是一致的。
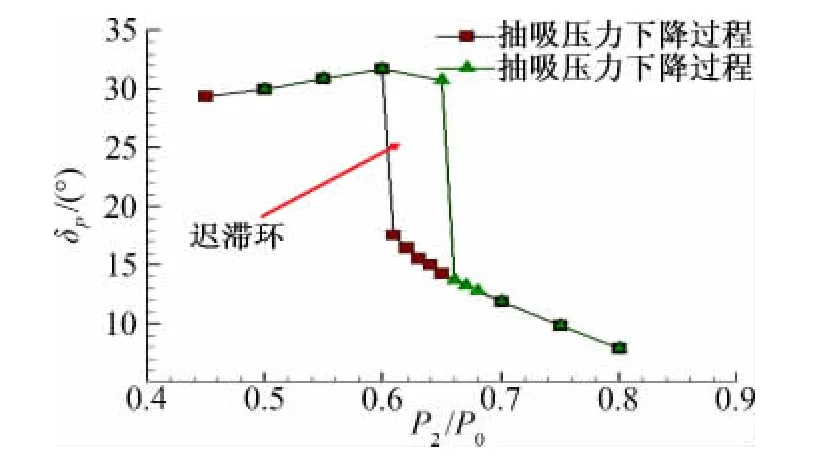
图6 抽吸压力增加对主流脱体的影响Fig.6 Effect of suction pressure increase on detachment
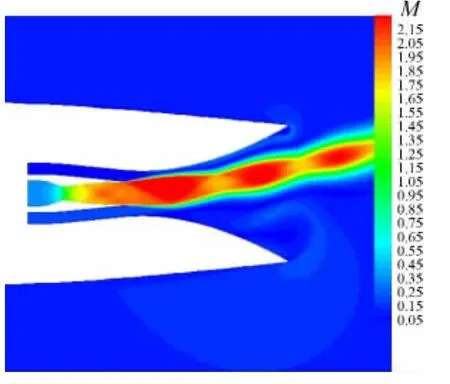
图7 二次流抽吸压力比增加0.66时流场图Fig.7 Flow field of CFTVN with P2/P0increase to 0.66
3.2 提高喷管压比实现附体主流脱体
在二次流抽吸压力为50.66kPa主流附体工况下,保持其它气动参数不变,研究了增加喷管压比实现附体主流脱体。主流压比NPR取值取值分别为:7.824、9、9.25、10。主流压比增加,主流动量增大,当原来作用在主流上的偏转力不足以提供主流沿外罩内壁面运动所需的离心力,从NPR=9.25开始,主流开始部分脱离外罩内壁面,如图8。另外,基本喷管设计压比为7.824,而此时喷管处于欠膨胀状态,主流在基本喷管出口下游继续膨胀,即使仍有少部分膨胀至外罩壁面,但不再沿着壁面流动,即完成了主流附体的脱离。
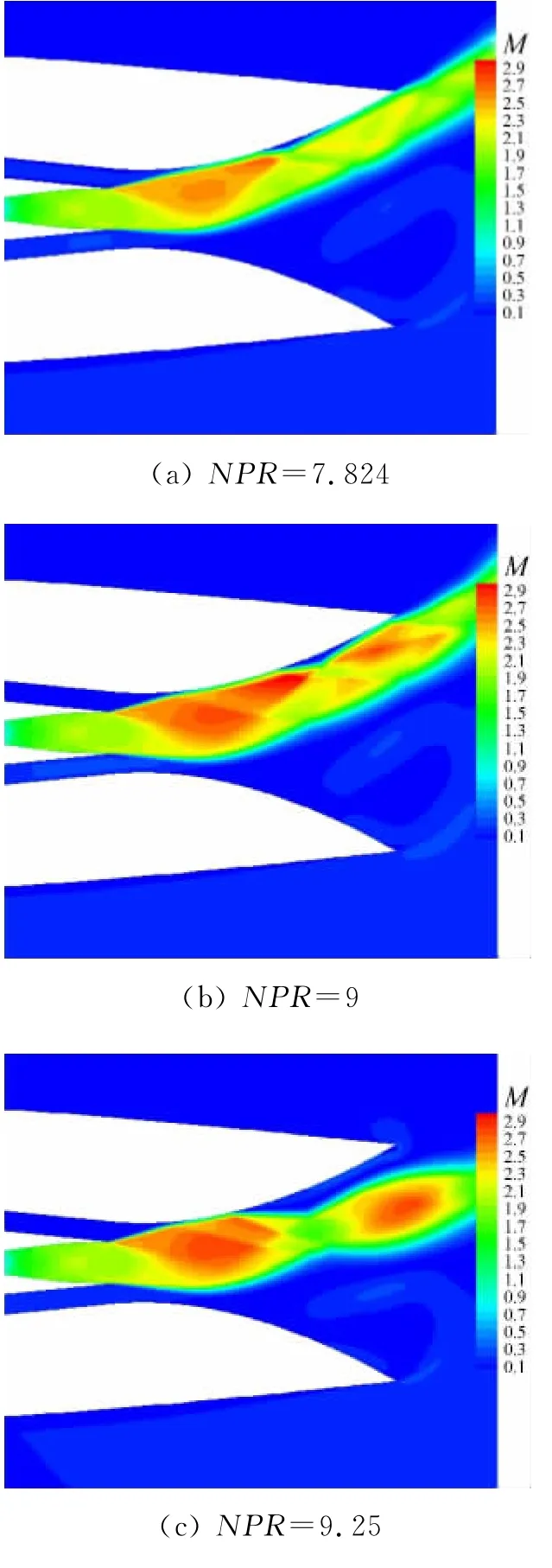

图8 不同NPR下流场图Fig.8 Flow field under different NPR
4 结 论
本文基于CFD数值模拟技术,对逆流推力矢量喷管主流附体形成机理、流场特征及实现附体主流脱体的方法进行了研究,结论如下:
(1)逆流推力矢量喷管主流附体的产生与二次流抽吸、主流卷吸及逆流剪切层有关。存在使主流附体的临界二次流抽吸压力,本文研究的模型中,二次流抽吸压力为61.86kPa时主流附体,低于该压力值,改变二次流抽吸压力对推力矢量角几乎无影响。
(2)提出了采用提高二次流抽吸压力和增大喷管主流压比实现附体主流脱体的控制方法,并验证了其有效性。
(3)通过增大二次流抽吸压力实现附体主流脱体的过程中,存在明显的滞后现象,即在推力矢量角随二次流抽吸压力变化的曲线图上形成迟滞环。
[1]KAREN A D.Summary of fluidic thrust vectoring research conducted at NASA Langley Research Center[R].AIAA 2003-3800.
[2]JIMENEZ A.Thrust vectoring for advanced fighter aircraft,propulsion package development[R].AIAA 2001-3991.
[3]BENJAMIN G Q.Fundamental conception of vectored propulsion[J].J.Propulsion,1990,6(67):747-75.
[4]MANGIN B,CHPOUN A,JACQUIN L.Experimental and numerical study of fluidic thrust vectoring of a two dimensional supersonic nozzle[R].AIAA 2006-3666.
[5]王占学,王玉男,李志杰,等.基于激波控制的流体推力矢量喷管推力矢量喷管试验[J].推进技术,2011,31(6):751-756.(WANG Z X,WANG Y N,LI Z J,et al.Experiment on fluidic thrust vectoring nozzle based on shock control concept[J].JournalofPropulsionTechnology,2011,31(6):751-756.)
[6]MILLER D N,YAGLE P J,HAMSTRA J W.Fluidic throat skewing for thrust vectoring in fixed geometry nozzles[R].AIAA 99-0365.
[7]KENRICK A W,KAREN A D.Experimental and computational investigation of multiple injection ports in a convergent-divergent nozzle for fluidic thrust vectoring[R].AIAA 2003-3802.
[8]STRYKOWSKI P J,KROTHAPALLI A.The counterflow mixing layer-strategies for shear-layer control[R].AIAA 93-3260.
[9]STRYKOWSKI P J,KROTHAPALLI A,WISHART D.Enhancement of mixing in high-speed heated jets using counter-flow nozzle[J].AIAAJournal,1993,31(11):2033-2041.
[10]Van Der VEER M R,STRYKOWSKIT P J.Counterflow thrust vectoring control of subsonic jets:continuous and bistable regimes[J].JournalofPropulsion andPower,1997,13(3):412-420.
[11]GILLGRIST R D,FORLITI D J,STRYKOWSKI P J.On the mechanisms affection fluidic vectoring using suction[J].JournalofFluidicEngineering,2007,129:91-96.
[12]HUNTER C A,DEER K A.Computational investigation of fluidic counterflow thrust vectoring[R].AIAA 99-2669.
[13]DORES D,MADRUGA SANTOS M.Characterization of a counterflow thrust vectoring scheme on a gas turbine engine exhaust jet[R].AIAA 2006-3516.
[14]汪明生,杨建军.逆流推力矢量喷管流动自身导致的非定常现象[J].航空学报,2009,30(4):630-636.(WANG M S,YANG J J.Flow induced unsteady phonmena in counterflow vectoring nozzles[J].ActaAeronauticaetAstronauticaSinica,2009,30(4):630-636.)
[15]邹欣华,王强.不同飞行条件下反流控制矢量喷管的内流特性[J].北京航空航天大学学报,2011,37(2):227-230.(ZOU X H,WANG Q.Internal performance of counterflow thrust vectoring nozzle under different flight condition[J].JournalofBeijingUniveisityofAeronauticsandAstronautics,2011,37(2):227-230.)
