扰动风作用下多段翼型流动的数值模拟及流动控制
2013-11-09李孝伟
李 亮,李孝伟
(上海大学 上海市应用数学和力学研究所,上海 200072)
0 引 言
现代飞行器设计中必须考虑各种特殊的环境,扰动风作为其中一种不可避免的因素,已经在当今飞行器研究中引起了高度重视。
从20世纪50年代到现在关于飞行器在扰动风和阵风作用的响应的研究已经很多[1-8],主要集中在试验和CFD数值计算方法。在实验方面,对于模拟阵风的形式是件很重要的事,目前一般是通过阵风发生器(或者加入一些能引起流场扰动作用的控制体)产生扰动风,由于受到阵风发生器参数与阵风形式对应等问题,试验中采取的阵风形式的研究比较单一和笼统。在数值计算方面,文献[7-8]中发展了一种网格速度方法,该方法以网格速度代替扰动运动的方法,既避免了数值振荡导致的计算不稳定[9],又得到了精确的数值结果。接着杨国伟等人发展了一种基于CFD与ARMA降阶模型结合的阵风响应分析方法,并通过分析比较知道了正弦阵风响应的参数辨识模型与CFD模型直接计算结果拟合程度最好的结论,建立的ARMA模型能用于任意形状阵风响应分析,大大提高了阵风响应计算的效率。以上研究均表明,在阵风和扰动环境下,飞行器的气动性能会发生严重的波动,甚至引起飞行的不稳定性。
从飞行的角度来说,人们期望这样的波动或不稳定性尽量少的发生,或者能采取一定的办法来抑制扰动风的负面作用。从流体力学的角度来说,抑制扰动风作用的最有效的办法是进行流动控制。
对于目前常见流动控制的研究方法[10-12]:吹气和吸气、微射流、零质量射流、等离子体、磁流体动力、涡流发生器、机翼上翼刀运动等;主要集中在对流场中出现流动分离进行控制及机翼增升减阻的研究;也有通过采取飞行器上机翼的运动对流场进行控制的研究。从发表的文献来看,目前对飞行器在扰动风作用下的流动的控制研究很少。
基于此,本文拟对多段翼型在扰动风作用下的非定常流动及其控制进行研究。由于机翼的机械运动相对于采取吹气和吸气、微射流、零质量射流等更具有改变流场区域的能力,因此本文采用襟翼摆动的方法进行流动控制。在襟翼的摆动过程中,襟翼和主翼之间存在相对运动,所以,在网格布局时采用了动态嵌套网技术。借鉴文献[7]的做法,采用网格速度方法模拟扰动风。系统地研究了在扰动风作用下多段翼型上的升力的响应规律;进一步研究了襟翼的摆动幅值和摆动相位对扰动风影响的作用规律,研究表明,针对一定范围的扰动风,可以找到合适的襟翼摆动幅值和提前相位角来有效地控制多段翼型上的升力波动。
1 数值方法
1.1 主控方程
本文采用了有限体积积分的二维非定常Navier-Stokes方程[13]:
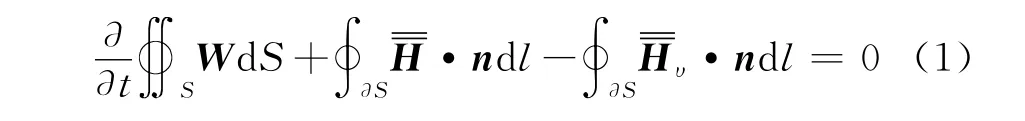
其中,
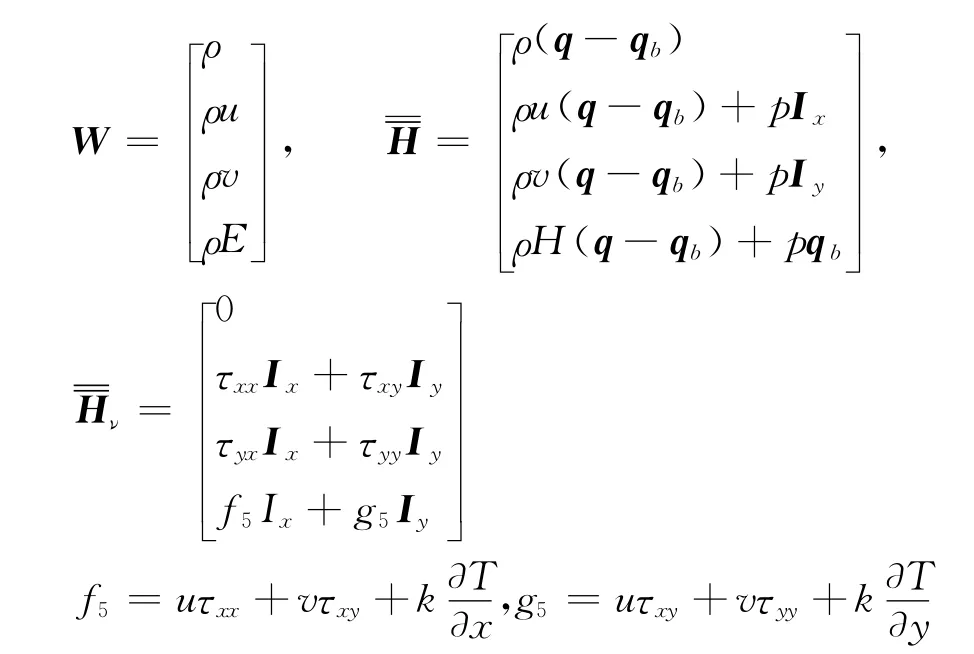
式中,ρ、(u,v)、E、H、p、T分别为流体的密度、速度q在绝对坐标系下的两个分量、总能、总焓、压强、温度;q、qb分别为流体质点的绝对速度、控制体表面的绝对速度;Ix、Iy分别为惯性系坐标轴方向的单位矢量,k为热传导系数。数值计算中采用的湍流模拟为BL模型。对于式(1)的求解,采用是中心有限体积格式和双时间推进法,具体请参见文献[14-15],在此不再叙述。
1.2 网格速度技术和动态嵌套网格
网格速度法是根据相对运动的思想提出的[7],就是用网格速度来间接的计入对应来流速度部分,如果网格速度为u,相对于计算区域在网格不动的情况下整体受到-u的来流速度的作用。在本文翼型所受到的扰动风变化就通过整体网格速度的方法间接代替,即所有网格区域上的点具有与扰动风对应的网格速度,但网格区域的点在空间上不具有因为网格速度引起的位置变化。
嵌套网格主要包括两个部分:将整个计算区域分成多个相互之间具有重叠部分的子区域,分别建立各个子区域的内外边界条件;建立各个子区域的信息传递关系。对于本文中研究的多段翼型的襟翼每一个运动时刻,襟翼与主翼之间位置关系都在发生变化,因此需要对每一个非定常计算的时刻,重新建立主翼与襟翼之间网格嵌套关系。对于每块网格插值边界位置条件随网格嵌套关系的变化而发生变化,因此在对于每一非定常计算的时刻,都要重新建立插值边界点的插值位置关系,从而使得嵌套网格之间的信息交换时刻保持对应性。对于本文中多段翼型在扰动风作用的流动控制的研究中,由于扰动风变化使用了整体网格速度代替,因此无论襟翼与主翼之间的相对位置关系是否发生变化,主翼和襟翼网格都具有与扰动风速度对应的网格速度。虽然所有的网格区域具有与扰动风速度对应的网格速度,但在计算插值过程中并没有考虑代替扰动风速度的那部分网速度引起机翼在空间位置上的变化。对于每个插值点的信息都是绝对坐标下的速度信息,每一个网格点的速度也是绝对坐标下的网格速度,与本文中的数值求解方法是没有任何冲突。
2 数值方法验证
2.1 网格速度代替扰动风技术的验证
用网格速度技术的方法对NACA0006翼型在受如图1中所示的阵风作用下的升力响应进行了数值计算,计算网格为202×61的C型网格。阵风Wg与来流V垂直,取Wg/V=0.08,从而导致机翼迎角突然增大到α=4.4°(0.08rad)。图2中给出了不同马赫数下单位迎角变化引起翼型升力系数变化值CL/α随无量纲时间S=2Vt/c(c为机翼弦长)的变化历程,图中标记为“present”,并与文献[6]中计算结果(图中标记为“Ref.[6]”)进行了对比,二者符合很好。基于Lomax在活塞理论基础上对线性可压缩流动中平板翼型突然增加迎角α时阵风响应的初始阶段导出的理论解[6]:
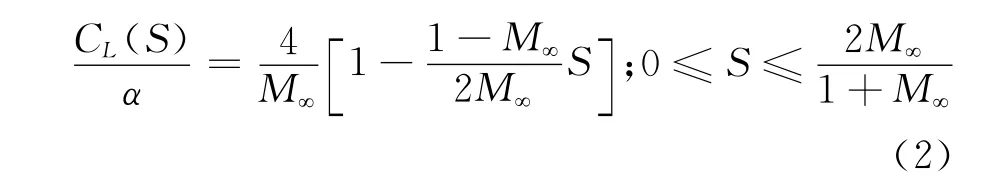
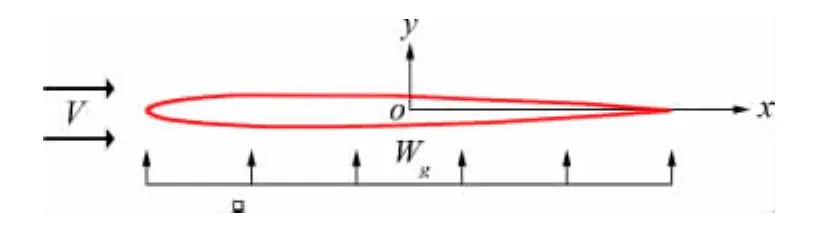
图1 NACA0006所受阵风示意图Fig.1 Schematic diagram of NACA0006in gust
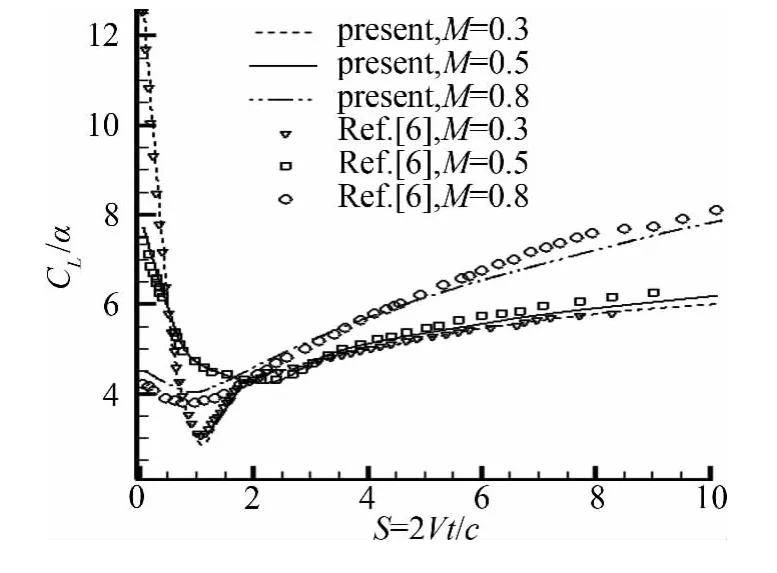
图2 升力响应计算结果与文献计算结果比较Fig.2 Comparison of lift response for gust with Ref.[6]
如图3中给出了该理论与计算结果的比较,理论解用“Exact”进行标记,计算解用“CFD”进行标记。可以看出,计算结果与理论解是一致的。由此说明,用网格速度法处理扰动风的办法是可靠的。
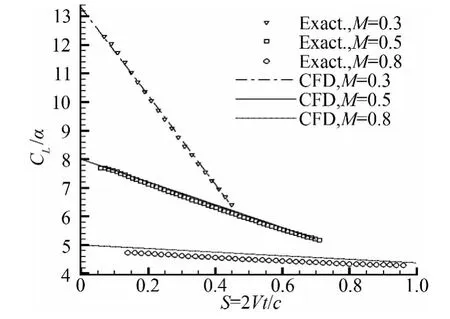
图3 升力响应计算结果与理论解比较Fig.3 Comparison of lift response for gust with exact result
3 扰动风作用下多段翼型的气动力响应计算
由于飞行器在飞行过程中受到扰动风影响最敏感的方向是垂直于来流方向,因此本文选取如图4所示的扰动风形式进行研究。扰动风速度方向与来流速度方向垂直,其函数形式:fg(t)=sin(2πft)。可以得到“网格速度”的函数为:
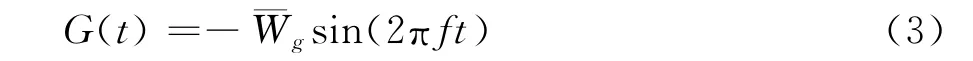
式中:为扰动风函数的扰动速度幅值,f为扰动风函数周期变化的频率。

图4 多段翼型所受扰动风形式示意图Fig.4 Schematic diagram of multi-element airfoil in gust
数值计算中,主翼计算网格为291×61的C型网格,襟翼计算网格为209×41的C型网。网格间的嵌套关系为如图5所示。主翼网格为A,A-HD为主翼网格挖洞区域;襟翼网格为B,B-HD为襟翼网格挖洞区域。襟翼与主翼之间的夹角θ0为10°。状态参数M∞=0.15,Re=2.2×106,迎角α0为5°。
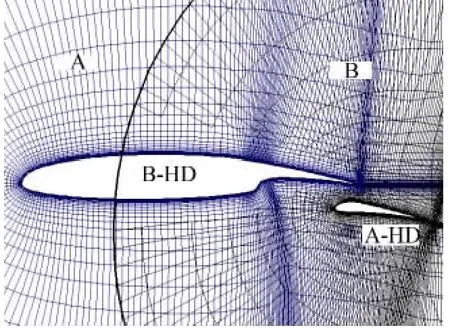
图5 主翼网格和襟翼网格之间嵌套关系Fig.5 Overlapping relation between main wing grid and flap grid
对于上述的扰动风形式,取f=0.0306、0.0153、0.0076和/V∞=0.02、0.08组合的6种情况下的扰动风进行了计算。得到了多段翼型主翼上的升力CL1、襟翼上的升力CL2、及整体机翼上的升力CLZ随无量纲时间S=tf变化的历程。如图6所示,在此给出了(f=0.0306,V/Wg=0.02)这一种情况下机翼升力变化的曲线CL/S;主翼、襟翼、整体机翼变化曲线分别标记为:“Main Wing”、“Second Wing”、“All Wing”。从中可以看到,几条升力曲线都呈周期性变化,其频率f*与扰动风频率f很接近。假设f*=f,由此主翼上的升力CL1、襟翼上的升力CL2、及整体机翼上的升力CLZ的函数可以分别近似为:
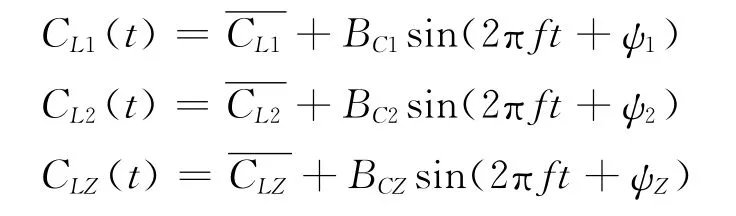
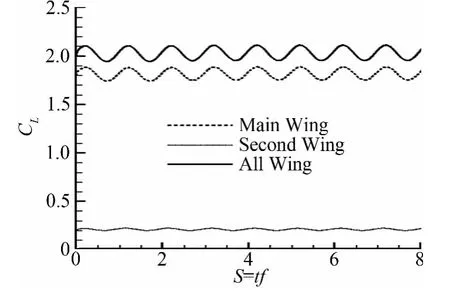
图6 机翼升力系数随时间变化的关系Fig.6 Relationship between lift coefficient and time
由上式去掉各个函数的平均值部分得到主翼、襟翼、整体机翼上升力波动随时间的波动函数分别为:
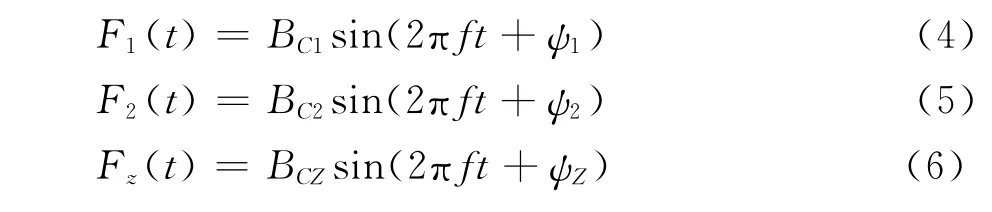
波动函数幅值与机翼受到扰动风引起的升力波动强度对应,而波动函数的相位差反应是机翼升力响应滞后相位。再利用机翼上升力在一个稳定循环周期内随时间变化的数据,通过参数辨识,可以近似得到BC1、BC2、BCZ、ψ1、ψ2、ψZ参数。
那么对于频率相同、扰动风速度幅值不同机翼上升力响应波动函数变化规律如何,在表1中给出了扰动风速度幅值为/V=0.02,0.08,扰动风频率为f=0.0306,的两种情况下的上述各参数值,并将这两种情况下对应升力系数拟合函数的波动幅值、相位进行了比较;其中N.1、N.2分别表示上述两种扰动风情况下各个翼型升力系数函数的参量,N.2/N.1表示这两种情况下辨识的参量的对应比值。结果表明:各升力系数函数对应的波动幅值BC(BC1,BC2,BCZ)与扰动风函数速度变化幅值近似成正比关系;而扰动风速度幅值的变化对各个函数的相位差ψ(ψ1,ψ2,ψZ)的影响不大。
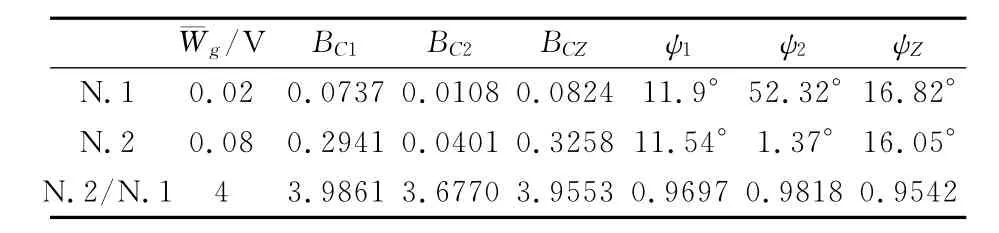
表1 主翼、襟翼、及整体翼型上升力系数拟合函数相关参数Table 1 The parameters of fitting function about the lift coefficient fluctuate of the wing
上述给出的都是襟翼与主翼夹角θ为10°时,扰动风作用下机翼升力响应的波动函数参数。那么对于襟翼(绕图4中固定点Q)相对于主翼取不同位置θ=2°~18°,在具有相同幅值(=0.02V)和频率(f=0.0306)的扰动风作用下,机翼上升力响应对应的波动函数的参数与襟翼夹角关系如何呢?
在此对襟翼相对主翼不同位置夹角θ,用相同的上述扰动风作用下机翼上升力响应进行了数值研究,得到了机翼上升力响应曲线,为了进一步说明流场中襟翼夹角与各个机翼升力波动函数参数之间关系,采用参数辨识得到各个波动函数参数。如图7、图8所示,分别给出了主翼、襟翼、整体机翼上升力响应波动函数幅值BC(BC1,BC2,BCZ)和相位差ψ(ψ1,ψ2,ψZ)与襟翼相对于主翼夹角θ的关系曲线。从图中可以看出,对于襟翼相对于主翼不同夹角θ情况下,相同扰动风作下主翼、襟翼、整体机翼上升力波动响应函数的幅值几乎没有多大变化;主翼升力波动函数的相位差在不同襟翼夹角位置情况下的值几乎没变,虽然襟翼上升力波动函数相位差值受襟翼夹角不同的影响比较大,但由于襟翼上升力波动函数的幅值相对于主翼上升力波动函数幅值较小,因此从图中可以观察到襟翼夹角θ对ψZ的影响比较小。
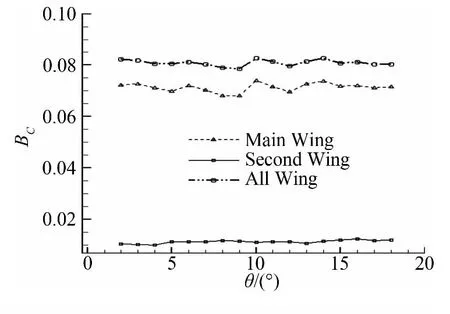
图7 机翼升力波动幅值与襟翼夹角的关系Fig.7 Relationship between wave amplitude of lift and position angle of flap
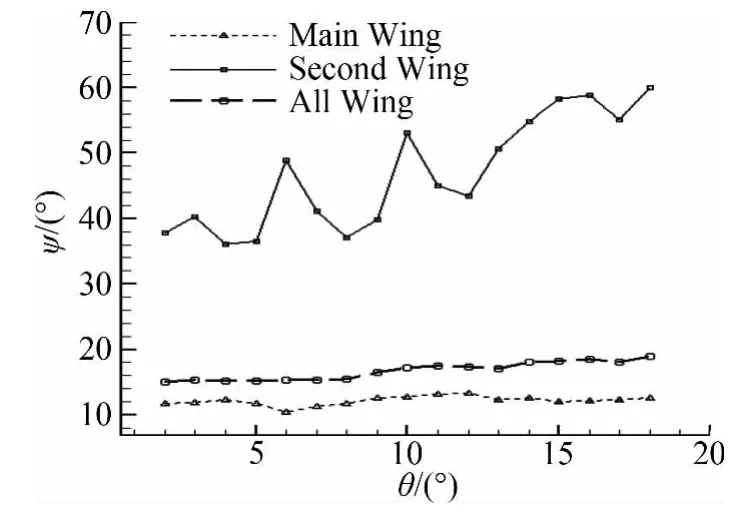
图8 机翼升力波动函数相位差与襟翼夹角的关系Fig.8 Relationship between phase difference of lift fluctuate function and position angle of fla
4 襟翼摆动对扰动风环境下多段翼型的流动控制
由前面的研究可以看出,在扰动风作用下,多段翼型上的升力会出现波动,这样会影响飞行器在空中飞行的平稳性。针对空间上大尺度的扰动风带来的波动,采取翼型的机械运动来进行控制,效果会如何呢?下面就进行一些研究。
由于这类扰动风在形式上对机翼升力的影响具有统一性。下文就其中一种扰动风参数情况(即g=0.02V、f=0.0306)进行控制研究;襟翼运动以文献[16]中襟翼运动形式为参考,襟翼绕以固定中心和一定夹角(θ0=10°)做周期性摆动运动,襟翼相对于主翼位置夹角θ随时间变化的函数形式为:
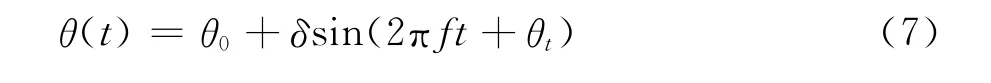
式中:θ(t)、θ0、δ、θt分别为襟翼相对于主翼的位置夹角、平均夹角、夹角变化幅值、襟翼摆动函数可控相位差。
4.1 无扰动风作用襟翼摆动对多段翼型升力的影响
在研究襟翼摆动对多段翼型在扰动风作用下的流动控制作用之前,研究一下无扰动风作用下襟翼摆动对多段翼型升力特性的影响是必要的,因为它有助于了解襟翼摆动对机翼的升力的影响作用。
为此,让襟翼绕固定点Q(如图4中所示的Q点)做周期性摆动,函数形式为式(7),取频率f=0.0306。如图9中给出了无扰动风作用下襟翼绕固定点(如图4中Q点)做周期性摆动(摆动幅值δ=3°、襟翼摆动函数可控相位差θt=0°,)时,机翼上升力CL随无量纲时间S=tf的历程变化;从中得到主翼、襟翼、整体翼型上升力函数随时间变化曲线也具有周期三角函数形式,在此近似给出主翼、襟翼、整体翼型上升力系数波动部分的波动函数分别为:
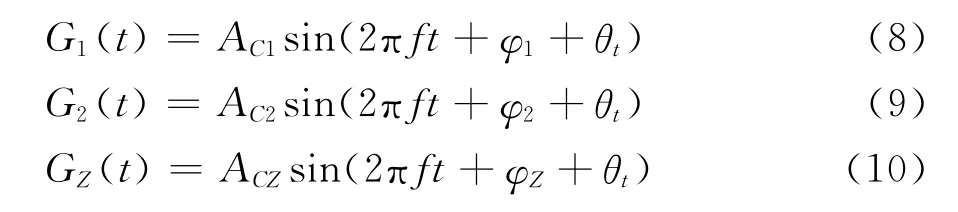
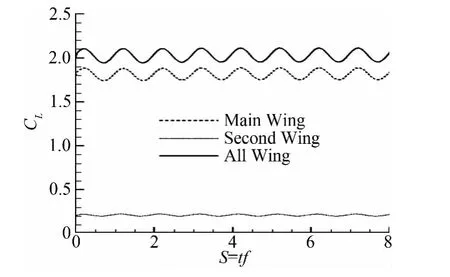
图9 机翼升力系数随时间变化的关系(襟翼摆动运动)Fig.9 Relationship between lift coefficient and time(flap oscillating)
通过参数辨识,得到各个波动函数的参数。如图10所示,给出了主翼、襟翼、整体机翼上升力波动幅值AC(AC1,AC2,ACZ)随襟翼摆动角变化幅值δ的变化曲线AC(AC1/δ,AC2/δ,ACZ/δ)。从图中可以看出,襟翼升力的波动幅值随着襟翼摆动幅值的增大而增大,几乎成线性比例关系;主翼升力的波动幅值随摆动幅值增加的变化不大;但整体机翼升力的波动幅值同样会随襟翼摆动幅值增大而增大,也是成单调递增的趋势。图11给出了主翼、襟翼、整体机翼上升力波动函数的相位角φ(φ1,φ2,φZ)随δ的变化曲线φ/δ(φ1/δ,φ2/δ,φZ/δ)。可以看出,总体升力相位差φZ在δ增加的过程中始终位于φ1和φ2值的中间;襟翼以不同摆动幅值δ(2°~6°)做摆动运动时,整体机翼上升力函数的相位差φZ(φZ≈6.8°)变化不是很大。

图10 机翼升力波动幅值与襟翼摆动角度幅值的关系Fig.10 Relationship between wave amplitude of lift and angle amplitude of flap swinging
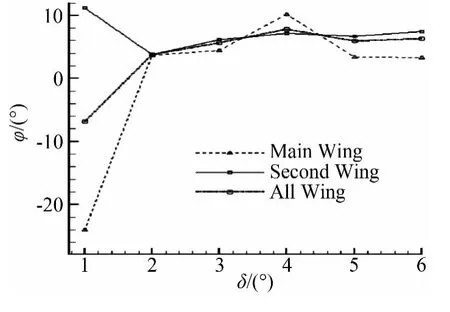
图11 机翼升力波动函数相位差与摆动角度幅值的关系Fig.11 Relationship between phase difference of lift coefficient fluctuate and angle amplitude of flap swinging
4.2 襟翼摆动幅值和相位角与控制机翼升力波动强度的关系
综述上面的研究表明:襟翼摆动作用(无扰动风作用)机翼上升力响应变化曲线(如图9)和只有扰动风作用(襟翼静止)机翼上升力响应变化曲线(如图6)具有类似的变化趋势。将襟翼摆动运动应用于对扰动风作用下机翼升力波动响应的控制研究中;如果能够找到适当的控制参数(襟翼摆动幅值δ和摆动提前相位θt)使得整体机翼在这两种情况下的升力响应曲线波动幅值相等,相位相差180°,从而就使得用着以参数进行控制,是否能达到减小机翼上升力波动响应强度呢?
考虑到襟翼做摆动运动对扰动风作用下机翼升力响应进行控制过程中,襟翼与主翼之间的夹角位置是变化的。借鉴第3节中研究的襟翼在不同位置夹角下(襟翼静止)扰动风作用机翼上升响应函数形式变化规律。由式(3)~(5)形式给出扰动风作用下(襟翼静止,襟翼夹角在摆动范围内)机翼升力响应的波动部分的波动函数的平均表达式:
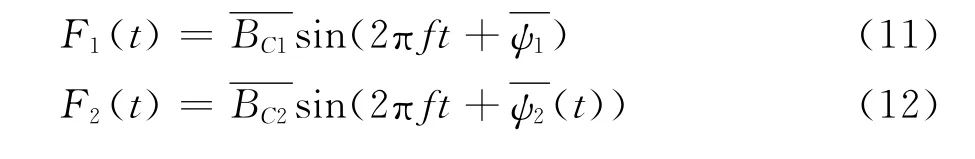
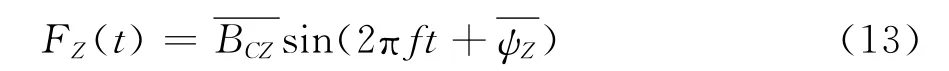
其中:对整体机翼上升力波动函数参数=0.0824,=17.8°。
由此进一步假设对于在扰动风作用下襟翼摆动运动能进行控制的参数(即襟翼摆动角幅值δ和襟翼运动提前相位角θt)。由此给出了扰动风作用下襟翼控制流场对机翼升力波动影响的波动函数:
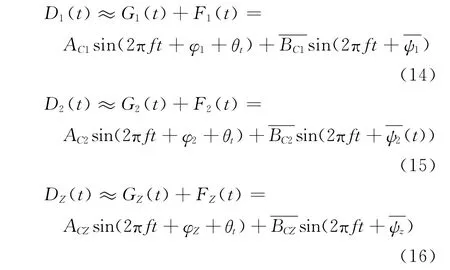
为了使得主翼上升力波动函数DZ(t)=sin(2πft+θCZ)的幅值最小,令DZ(t)=0得到:ACZ=;θt=180°+-φZ;进一步根据图10和图11中个机翼波函数的幅值(ACZ)、相位差(φZ)与襟翼摆动角度幅值δ的关系图中那个得到对应:δ=3.36°,φZ=6.8°。由此得到近似解在襟翼以角度幅值δ=3.36°,提前相位角度θt=191°时,使得整体机翼升力波动变得最小的控制参数。
如图12给出了这一控制条件下,机翼主翼、襟翼、整体机翼升力时间函数曲线,从中与图6中没有控制情况扰动风影响下曲线对比,整体机翼升力曲线的波动变的平缓多了,说明得到襟翼摆动控制参数的解析解有很好知道对扰动风影响波动控制研究的指导作用。
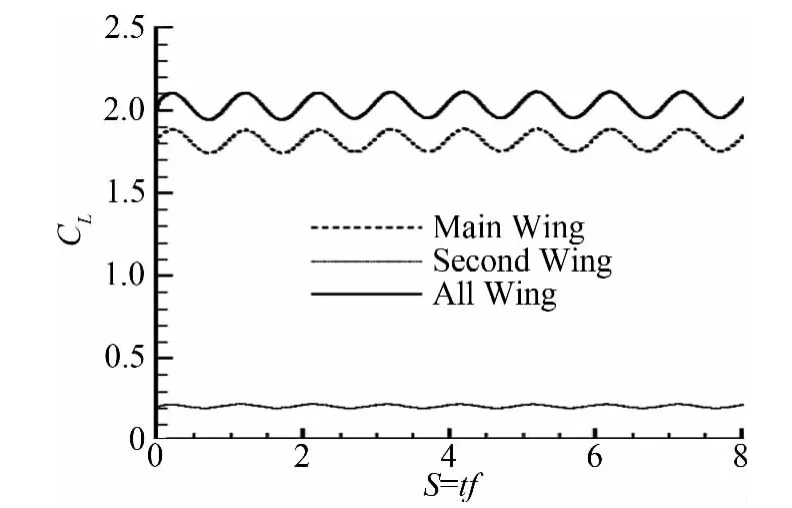
图12 在襟翼在解析参数解控制参数条件下,机翼升力随时间变化的关系Fig.12 Relationship between lift coefficient and time(at the control parameters solution by equation)
为了进一步说明襟翼摆动角度幅值δ和相位提前角θt对扰动风作用下机翼升力波动影响控制作用的规律。如图13,给出了多段翼型主翼、襟翼、整体机翼升力波动函数幅值DZ与襟翼提前角θt的关系。从图中可以看出随着襟翼摆动提前角θt的变化,整体机翼升力波动函数幅值先随襟翼摆动提前角θt的增大而减小,后面随襟翼摆动提前角θt的增大而曾大;机翼升力波动函数幅值存在最小值,其对应的襟翼摆动提前相位角为198.6°,与上面近似解得到的θt=191°很接近,但有些小差别,这可能是由于在去扰动风影响下机翼升力波动函数相位形式上有一定偏差。如图14,给出了多段翼型主翼、襟翼、整体机翼升力波动函数相位差θC与襟翼提前角θt的关系。从图中可以看出,襟翼升力时间波动函数相位差随襟翼摆动提前相位θt的递增而变大;整体机翼升力时间波动函数相位差随襟翼摆动提前相位θt变化曲线在θt=198.6°附近有较大的转变;并且襟翼升力波动函数相位差与主翼升力函数数相位差的差值在θt=198.6°附近时与180°很接近。
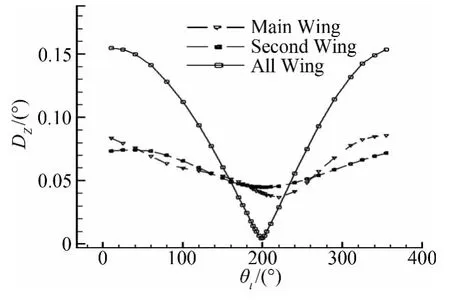
图13 机翼升力波动幅值与襟翼提前相位角的关系Fig.13 Relationship between wave amplitude of lift and phase angle of flap before gust functions
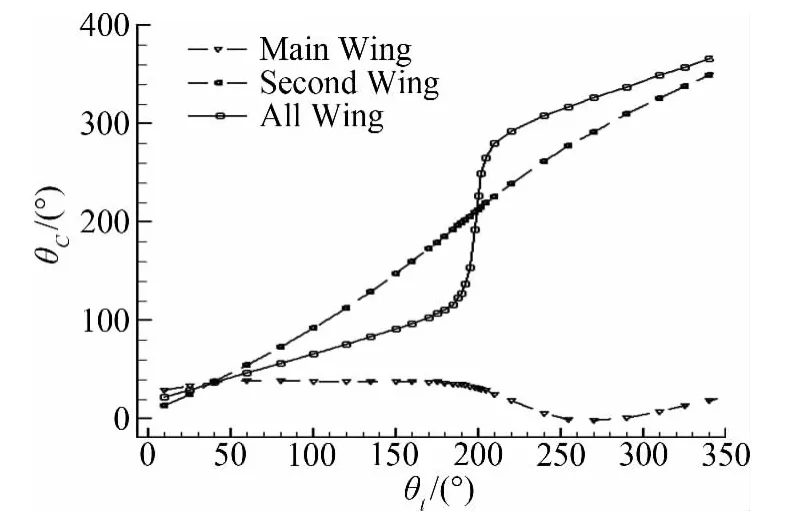
图14 机翼升力波动函数相位差与襟翼提前相位角的关系Fig.14 Relationship between phase difference of lift fluctuate function and angle of flap before gust functions
4.3 襟翼摆动对机翼升力波动强度的控制律
通过上文对具有特定频率和幅值的扰动风进行控制的研究表明:分别对只有扰动风或者只有襟翼摆动的情况进行研究,得到了特定扰动风作用下,襟翼摆动使翼型升力波动影响最小的控制参数。进一步对不同频率、不同幅值的扰动风作用下多段翼型的流动进行了研究,并给出在具有一定频率和幅值范围的周期性扰动风作用下,采取襟翼摆动的方式进行控制的控制参数δ、θt的近似表达式。
定义扰动风频率和扰动风速度幅值与前面研究特定扰动风的频率和幅值的关系为:
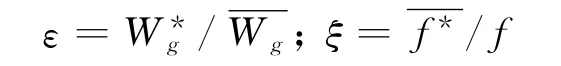
其中:ε为当前扰动风幅值与初试扰动幅值的比值;ξ为当前扰动频率与初试扰动风频率f的比值。
可得扰动风的形式为:
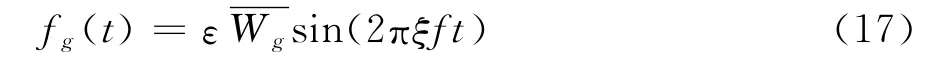
则襟翼摆动控制方程形式为:

研究表明,对于式(17)中形式的扰动风,当扰动频率比值ξ∈(0.25,3.75),扰动幅值比值ε∈(0.5,2),并且这两个系数的乘积ξε∈(0.16,4)时,能得到翼型在此种扰动风作用下,使升力响应波动尽量减小的襟翼摆动控制参数δ、θt与ε、ξ关系表达式:
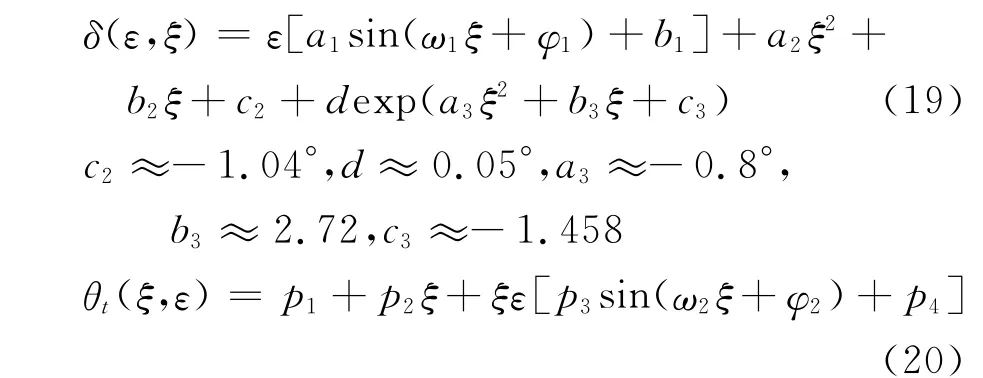
式中:p1≈203°,p2≈-4.5°,p3≈0.5656°,ω2≈1.19,φ2≈-5.958,p4≈-0.556°。
5 结 论
本文通过对多段翼型扰动风作用下的气动性能及其流动控制的研究得到以下结论:
(1)在与来流方向垂直的周期性扰动风作用下,多段翼型的主翼、襟翼、整体机翼上升力响应波动函数的频率与扰动风频率大致相同,扰动强度幅值与扰动风速度幅值成正比,扰动风扰动幅值的大小对机翼升力波动函数相位差的影响不大,并且针对襟翼相对主翼不同位置夹角,同一周期扰动风作用下机翼整体升力波动函数相差不大;
(2)在一定的扰动风作用下,多段翼型上的升力波动强度变化与襟翼摆动角幅值和提前相位差有关,由此,通过建立升力波动函数和参数识别的办法研究后认为,存在合适的襟翼运动控制参数(襟翼摆动幅值和提前相位角),能明显减弱升力响应的波动强度,从而说明襟翼摆动是抑制扰动风负面影响、改善飞行平稳性的一种有效的流动控制措施。
[1]MILES J W.The aerodynamic force on an airfoil in a moving gust[J].JournalofAeronauticalSciences,1956,23(11):1044-1050.
[2]JMCCROSKEY W,GOORJIAN P M.Interaction of airfoils with gusts and concentrated vortices in unsteady transonic flow[R].AIAA 1983-1691-689,1983.
[3]MCCROSKEY W J.The effects of gusts on the fluctuating airloads of airfoils in transonic flow[J].Journalof Aircraft,1985,22(3):236-243.
[4]DUKE TANG,DOWELL EARL H.Experimental and theoretical study of gust response for high-aspect-ratio wing[J].AIAAJournal,2002,40(3):419-429.
[5]HORWICH E A.Unsteady response of a two-dimensional hydrofoil subject to high reduced frequency gust loading[D].[MS Thesis].Massachusetts Institute of Technology,1993.
[6]杨国伟,王济康.CFD结合降阶模型预测阵风响应[J].力学学报,2008,40(2):145-153.
[7]PARAMESWARAN V,BAEDER J D.Indicial aerodynamics in compressible flow-direct computational fluid dynamic calculations[J].JournalofAircraft,1997,34(1):131-133.
[8]詹浩,钱炜祺.翼型和机翼阵风响应的数值模拟[J].空气动力学学报,2007,25(4):531-536.
[9]LEISHMAN J G.Subsonic unsteady aerodynamics caused by gusts using the indicial method[J].JournalofAircraft,1996,33(5):869-879.
[10]肖中云,牟斌,等.零质量射流与分离流控制的数值模拟[J].空气动力学学报,2006,24(1):46-49.
[11]张攀峰,王晋军.合成射流控制NACA0015翼型大迎角流动分离[J].北京航空航天大学学报,2008,34(4):443-446.
[12]顾蕴松,明晓.大迎角非对称流动的非定常弱扰动控制[J].航空学报,2003,24(2):102-106.
[13]李孝伟.基于嵌套网格的全机带襟翼、副翼绕流的数值模拟[D].[博士学位论文].西北工业大学,1999.
[14]JAMESON A,SCHMIDT W,TURKEL E.Numerical solution of the Euler equations by finite volume methods with Runger-Kuuta time stepping schemes[R].AIAA Paper 1981-1259-845.
[15]JAMESON A.Time dependent calculation using multig-rid,with applications to unsteady flows past airfoils and wing[R].AIAA-1991-1596-607,1991.
[16]杜超.多段翼型非定常粘性绕流数值研究[D].[硕士学位论文].上海:上海大学,2007.
