跨声速风洞模型变形测量实验中标记点影响研究
2013-11-09邓小刚张征宇
孙 岩,邓小刚,张征宇,王 超
(1.中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳 621000;2.中国空气动力研究与发展中心 高速空气动力研究所,四川 绵阳 621000)
0 引 言
目前,随着风洞模型变形视频测量技术(Video Model Deformation,VMD)的发展与成熟,VMD开始被广泛应用于大尺寸风洞模型变形测量[1-5]与风洞模型的静动气动弹性特性分析中[6-9]。VMD技术通过在风洞模型表面粘贴或喷涂一定数量的标记点来记录模型表面的位移或变形[2],标记点的存在改变了模型表面的粗糙度和外形,从而对模型的气动特性产生影响,增加了模型气动力数据的不确定度[10]。因此,通常将变形测量实验和测力测压实验分开做,以消除标记点对测量数据的影响,但这样需要安排额外的风洞实验进行模型变形的测量,增加了实验的次数和成本,降低了实验的效率。
所以,研究变形测量实验中标记点对气动特性的影响规律,改善标记点的分布,使标记点对模型气动特性的影响在可接受的范围以内,对于同时进行变形测量实验和测力测压实验,提高实验效率、降低实验成本具有重要的参考价值。
由于风洞实验的成本过于高昂,VMD技术发展以来,研究人员主要通过降低标记点的厚度和数量来减小标记点的影响[11-13],尚未有实验对标记点的影响规律进行过系统的研究。计算流体力学(Computational Fluid Dynamics,CFD)方法相对风洞实验具有成本低、适应性广的特点,且定常气动力的求解技术已经趋于成熟,因此基于CFD开展标记点影响研究是比较经济可行的途径。
跨声速风洞模型变形测量的对象主要是大展弦比的运输机、民航客机或无人飞机模型,这类飞机的共同特点是采用在高亚声速巡航时具有良好升阻特性的超临界翼型以提高航程。通过研究标记点对跨声速超临界翼型气动特性的影响即可获得跨声速风洞模型变形中标记点对模型气动特性的主要影响规律。
为此,本文基于CFD研究了圆形标记点对超临界翼型RAE2822气动特性的影响,为跨声速风洞模型变形测量标记点的设计和布置提供一定的参考依据。
1 数值方法
1.1 控制方程及离散方法
二维直角坐标系下定常流动的守恒型控制方程是:
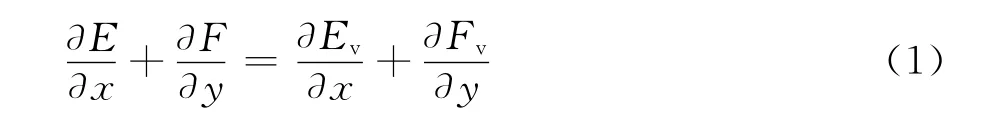
其中E、F分别为x、y方向的对流通量,Ev、Fv分别为x、y方向的扩散通量,变量的详细定义参考文献[14]。湍流模型采用单方程的 Spalart-Allmaras(SA)湍流模型,采用Roe通量差分离散空间对流项,粘性项采用中心差分离散。
1.2 数值精度验证
验证实例选择超临界翼型RAE2822的跨声速流场计算,RAE2822[15]是美国国家CFD应用研究项目(National Program of Applications Oriented Research in CFD,NPARC)的CFD验证与确认小组选择来验证计算代码Wind-US的例子。网格选择NPARC提供的369×65的C型网格(如图1a),计算Ma为0.729,迎角为2.31°,基于弦长的雷诺数Re为6.5×106,壁面压力系数Cp的计算结果与 Wind-US计算结果及实验结果对比见图1(b)。可见,在翼型壁面的大部分区域,本文压力系数计算结果与实验结果非常吻合,在激波位置附近,本文计算结果的压力值比实验值要大一些,激波强度要小一些,但同 Wind-US采用SA湍流模型的计算结果非常的一致,而采用SST模型的 Wind-US计算结果比采用SA模型的Wind-US计算结果和本文计算结果要差一些,因此湍流模型的选择对于激波位置的捕捉具有比较重要的影响,这和NPARC的验证结果是一致的。总体来说,本文采用的数值离散方法具有良好的计算精度。
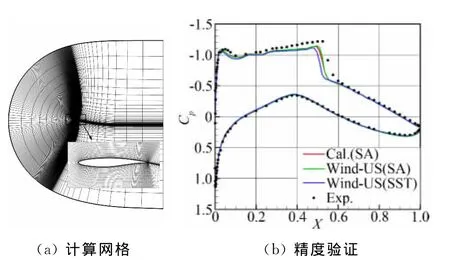
图1 计算网格与精度验证Fig.1 Mesh and precision validation
2 标记点及气动力影响系数定义
2.1 标记点的几何定义
风洞模型变形测量实验中可以采用的标记点有多种类型,如油漆喷涂、荧光涂料喷涂及机械钻孔填充油漆等,每种标记点具有各自的优缺点[2]。为了提高标记点的可识别性及识别精度,标记点的形状常采用圆形,如图2(a),因此,标记点的外形可以通过圆柱的几何参数进行定义,而在二维情况下标记点退化成一个矩形,如图2(b),d表示标记点的直径,t表示标记点的厚度。标记点中心在当地翼剖面弦向位置坐标用X表示。
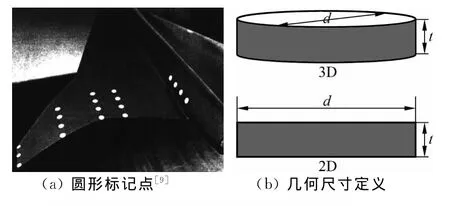
图2 标记点形状与尺寸定义Fig.2 Target shape and dimension definition
对于不同尺寸的风洞模型,由几何相似定理知标记点尺寸对模型气动特性的影响是相对的,因此利用模型的平均气动弦长作为参考尺寸,标记点的几何外形和位置通过相对尺寸来定义。
2.2 气动力系数影响因子
标记点被粘贴在风洞模型的表面,改变了模型表面的粗糙度及局部模型外形,从而改变了作用在模型表面上的气动力,定义标记点对气动力系数的影响因子IFC,用来描述标记点对气动力影响的程度,如式(2):

式中,C为风洞模型的气动力系数,σC为气动力系数C的误差限,对于跨声速风洞实验,国家军用标准GJB1061-91给出了误差限σC的取值,如表1。本文选取合格指标的σC值。
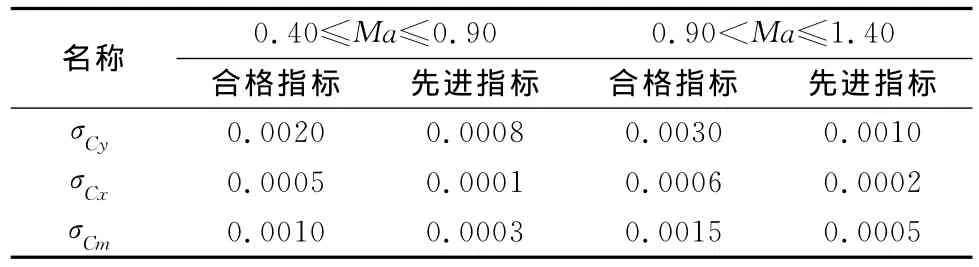
表1 高速风洞测力实验精度指标[6]Table 1 Requirement for force-test precision of high speed wind tunnel[6]
下标withTarget和withoutTarget分别表示有标记点和没有标记点时对应的气动力系数值。当IFC在-1和1之间时,表示标记点对于气动力特性的影响量在误差限以内,标记点的影响可以忽略不考虑,标记点布置方案合理;当IFC超出了这个范围,表示标记点对模型气动力特性的影响量已经超出了风洞实验允许的误差极限,标记点的影响不可忽略,必须重新设计标记点参数及布置方案,保证标记点对气动力特性的影响处在合理的范围。明显地,IFC分别受到标记点直径d、厚度t、位置X、标记点的组合方式Θ以及模型所处的外部流场条件Ω的影响,因此IFC可以通过下式的函数表示。
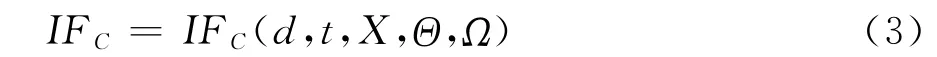
其中,
如式(3)、式(4),IFC是众多参数的函数,如果分析每个参数对IFC的影响,涉及的变量非常多,将会使得问题变得非常的复杂,极大地增加了计算量和问题研究的难度,因此,通过对参数和实际物理流动环境的分析,不考虑某些参数的影响。亚跨声速模型变形测量实验中,Ma和Re在一个固定的范围内变动,变化不是很大,因此假定Ma和Re的值不变,不考虑它们对标记点IFC的影响;标记点的直径d受到相机测量视场和模型尺寸的约束,尺寸如果过大,曲面喷涂标记点困难,机翼模型表面可以布置标记点数量就会受到限制,标记点之间的距离会减小,增大扭转角计算的误差,标记点直径d过小,标记点在图像上占据的像素会较小,标记点中心识别的精度会降低,降低标记点空间坐标的解算精度,标记点的直径选择一个利于提高测量精度的最优值。因此式(3)、式(4)可以简化成:

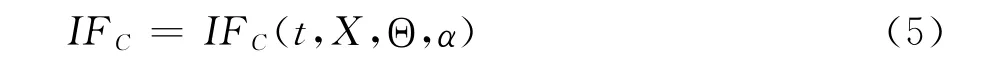
其中,标记点组合方式Θ是研究标记点之间的耦合作用对模型整体气动特性的影响。
跨声速大展弦比飞行器风洞模型的平均气动弦长c为150mm左右,标记点直径一般取12mm左右,因此标记点直径d的相对尺寸为0.08c,定义标记点厚度为6μm为一个厚度单位,用H表示,H的相对尺寸为0.00004c。
3 计算结果与讨论
通过3个Case分别研究不同条件下标记点对模型气动特性的影响规律,模型仍然采用RAE2822翼型,计算网格采用NPARC提供的369×65的C型网格,标记点在翼型表面的结构如图3所示,标记点的外形通过改变翼型边界得到,运动边界附近的网格通过弹簧原理运动得到新的网格,有关网格运动的弹性方法可以参考文献[16]。
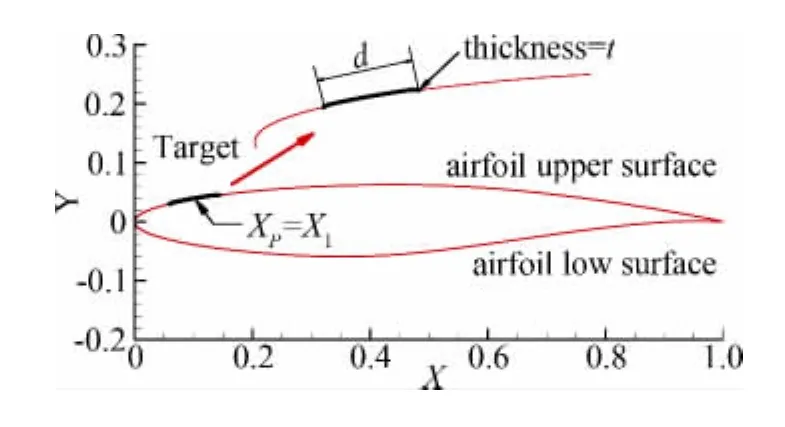
图3 标记点在翼型RAE2822上结构示意图Fig.3 Sketch of target on airfoil RAE2822
3.1 Case I:标记点厚度t与位置X影响
分别研究上下表面不同位置的不同厚度的标记点对翼型RAE2822气动特性的影响,标记点计算参数如表2。

表2 Case I计算参数Table 2 Computational parameters of Case I
图4给出了单个标记点对气动力系数影响因子的计算结果,俯仰力矩系数的参考中心为四分之一弦长处,下文相同。可以看出:
(1)气动力系数影响因子IFC随标记点的位置X变化较为明显,在沿弦向大部分区域,模型上表面标记点对气动力的影响量要明显大于同一弦向位置下表面标记点对气动力的影响量(翼型后缘附近位置除外),分析产生这一现象的主要原因是此时模型的迎角为正值,模型的上表面处于背风区,流场经过加速,速度值较大,标记点阻碍了气流的流动,因此对气动力的影响较大,而模型的下表面处在迎风区域,流场经过减速,气流速度较小,标记点对气流的阻碍作用较小一些,因此对气动力的影响较小,而在靠近翼型后缘位置处,气流在上表面减速,在下表面加速,同前缘流动正好相反,因此在靠近后缘的位置,下表面标记点对气动力的影响量比上表面标记点对气动力的影响量要大一些。
(2)随着标记点厚度t的增加,标记点对气流的阻碍作用加剧,标记点对翼型气动特性的影响呈现非线性的增长,厚度越大,气动力系数影响因子增长越快。
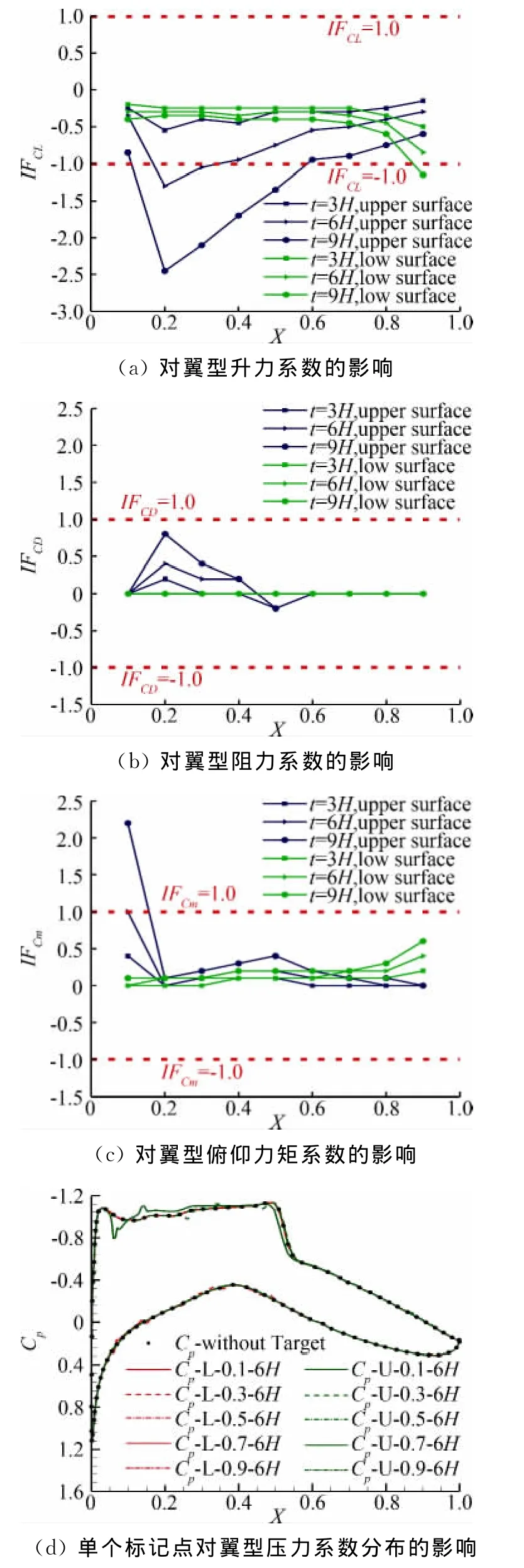
图4 单个标记点对翼型RAE2822气动特性的影响Fig.4 Single target effect on aerodynamic characteristics of RAE2822
(3)标记点对阻力系数CD的影响较小,对升力系数CL和俯仰力矩系数Cm的影响较大,主要原因是跨音速流动中,由于激波的产生,激波阻力占模型阻力很大一部分,标记点对气流阻碍作用在标记点后方很快得到恢复,仅对标记点附近的压力分布产生影响,对于激波强度影响很小,如图4(d),所以对阻力系数CD的影响较小,而标记点对局部的压力系数的影响造成了部分的升力损失,如图4(d),从而对升力系数CL和俯仰力矩系数Cm产生较大的影响。
(4)如图4(d),标记点对附近位置的压力系数的影响比较明显,在某些位置(如吸力峰位置,X等于0.1附近),压力系数改变量最大达到-0.2,因此如果在测压实验中需要进行模型变形测量实验,标记点的布置应该避开测压孔的位置,避免对测压孔压力测量产生影响。
3.2 Case II:不同迎角α下单个标记点影响
研究不同迎角状态下单个标记点对气动力系数的影响规律,计算参数如表3。

表3 Case II计算参数Table 3 Computational parameters of Case II
图5给出了不同迎角下的计算结果,可以看出:
(1)当模型的迎角α为负或者很小时,标记点处在气流的迎风区域,气流速度较小,标记点对气流的阻碍作用较小,气动力系数影响因子较小,而随着模型迎角α的增大,标记点从流场的迎风区域转移到流场的背风区域,标记点位置流场速度增大,标记点对流动的阻碍作用变大,从而使得气动力系数影响因子迅速变大,当模型迎角α为2°时,标记点对模型俯仰力矩系数Cm的影响量超过了风洞实验误差的允许值,当模型迎角α为4°时,标记点对模型升力系数CL的影响量已经远远超出了风洞实验误差的允许值。但当迎角进一步增大(α>4°),流动在上表面开始发生分离,标记点进入到分离区域,分离区域内的流场速度较低,且流动较为复杂,从而标记点对气动力系数影响因子的影响降低,表现为随着迎角的进一步增大,标记点对翼型气动特性的影响反而变小,如图5。
(2)在任意的迎角α下(α=2°除外),标记点对模型阻力系数CD的影响最小,对俯仰力矩系数Cm的影响次之,对模型升力系数CL的影响最大,同Case I的结果是吻合的,在α=2°时,标记点对俯仰力矩系数Cm的影响量比对升力系数CL的影响量稍大一些。
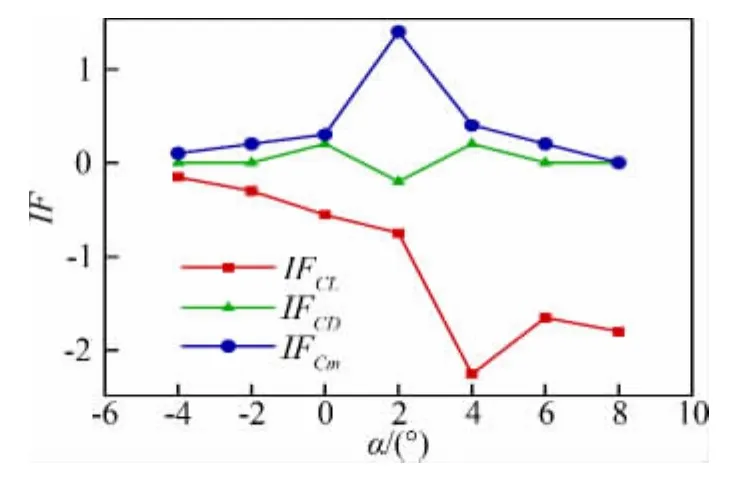
图5 不同迎角下的单个标记点影响系数Fig.5 Single target impact factor at different attack angles
3.3 Case III:标记点组合方式Θ的影响
通过四种不同的标记点组合方式,研究不同的组合方式下标记点对气动力特性的影响研究,为了准确计算模型剖面变形的弯曲扭转特性,每个剖面至少需要安置3个标记点,因此,采用三个标记点组合作为研究对象。从前面的研究得知,当模型迎角α为正时,上表面弦向靠后的位置标记点的影响较小,下表面弦向靠前的位置标记点的影响较小,所以组合方式采用上表面三点均布、上表面三点靠后均布、下表面三点均布、下表面三点靠前均布四种组合方式,四种标记点组合在翼型上的结构如图6所示。Case III的流场计算参数和Case I相同,标记点厚度为0H~9H,标记点位置参数如图6。
图7给出了四种标记点组合方式下标记点对翼型气动力系数的影响曲线,其中Θ1′、Θ2′、Θ3′及Θ4′分别对应四种不同组合方式中三个标记单独点对翼型气动力系数影响量之和。从图7中可以看出:
(1)标记点组合对阻力系数CD的影响依然很小,如图7(b),因此可以忽略标记点对阻力系数CD的影响作用。
(2)四种组合方式中,标记点组合后对升力系数CL的影响比单个标记点对升力系数的影响量之和要小,如图7(a),因此标记点之间的耦合作用使得组合后的标记点对升力系数的影响CL降低;四种组合方式,组合方式Θ1、Θ2的标记点影响随标记点厚度呈现非线性增加的方式,而组合方式Θ3、Θ4的标记点影响随标记点厚度呈现近似线性增加的方式,就增长速度来说,组合方式Θ2、Θ3的增长速度要快一些,组合方式Θ1、Θ4的增长速度要慢一些。
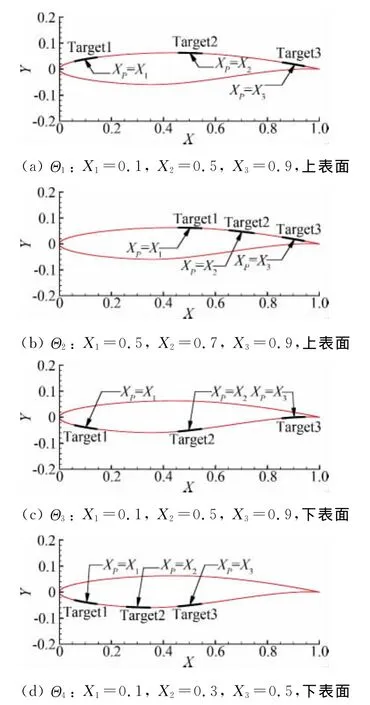
图6 翼型RAE2822上标记点组合方式Fig.6 Group types of targets on airfoil RAE2822
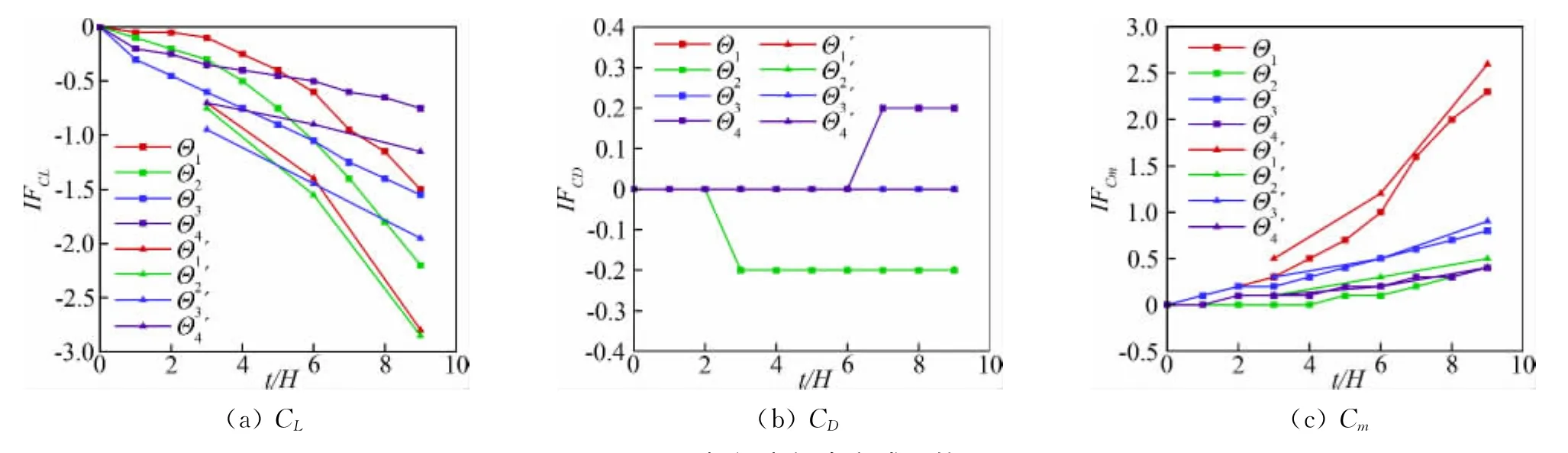
图7 不同标记点组合方式下的IFFig.7 Impact factor in different target group types
(3)组合方式Θ1、Θ2中,标记点组合后对俯仰力矩系数Cm的影响比单个标记点对俯仰力矩系数影响之和要小,而组合方式Θ3、Θ4中,标记点组合后对俯仰力矩系数的影响和单个标记点对俯仰力矩系数影响之和基本一样,如图7(c),说明组合方式Θ1、Θ2中标记点对俯仰力矩系数影响之间存在耦合,而组合方式Θ3、Θ4对俯仰力矩系数影响之间耦合关系非常小。
(4)综合比较,四种组合方式中,Θ4对气动力影响最小,而Θ1对气动力系数的影响最大。
3.4 进一步讨论
前面计算并分析了模型标记点参数对二维翼型气动特性的影响规律,当标记点厚度达到一定值时,如X=0.2时,t=6H即0.00024c(当地机翼弦长为150mm时,t=36μm),标记点对升力系数的影响值超过风洞实验允许的误差限,如图4(a)。在实际风洞实验中模型多采用三维机翼,标记点影响区域的展向尺寸δl相对于模型机翼的展长l是个小量,假设不同剖面标记点之间相互不影响,标记点对于全机气动系数的影响量可以近似用下式表示:
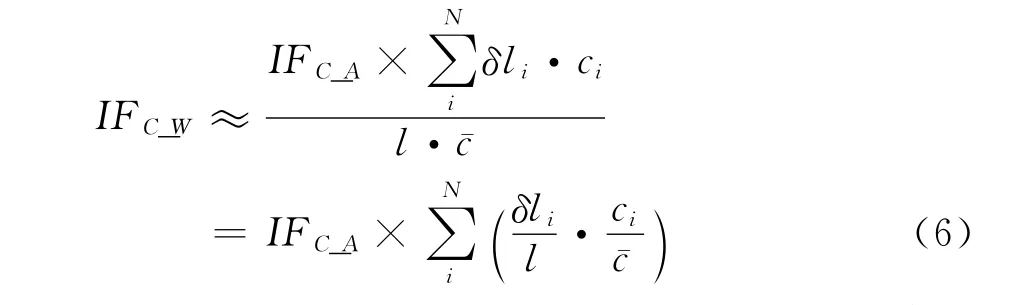
其中,IFC_W为标记点对机翼模型气动系数的影响因子;IFC_A为标记点对翼型气动系数的影响因子;N为展向分布的标记点数量;δli为第i个标记点影响区域的展向尺寸;ci为第i个标记点所在位置翼型剖面弦长;l为机翼展长;为机翼几何平均气动弦长;δli/l为一小量,ci与量级相同,因此当展向分布的标记点数量N比较少时,标记点对机翼模型气动系数的影响因子IFC_W是一小量,可以忽略不计。如X=0.2,t=9H时(c=150mm时,t=54μm,很多漆膜是可以满足这个厚度要求的),标记点对翼型升力系数的影响因子为-2.5,如图4(a),标记点的直径为d=12mm,假设标记点影响区域的展向尺寸δli=3d=36mm,模型的展长l=1500mm,则:
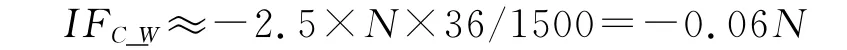
当N小于16时,IFC_W<1.0,标记点对模型机翼的升力系数影响可以忽略。而当标记点沿展向分布数量N比较多时,标记点对机翼气动系数的影响就不再是一个小量,就需要考虑标记点对气动特性的影响了。
图8给出了某三维机翼模型上表面上一种标记点布置方案和标记点对模型气动特性的影响曲线(Ma=0.75,ReL=3.0×106,α=2°)。机翼半展长为530mm,沿展向共分布10排标记点,每排标记点数目为3个,分别位于当地翼剖面弦向位置的0.1、0.5和0.9处,机翼的平均气动弦长为131.9mm,标记点的直径为11mm,如图8(a)。随着标记点厚度的增加,标记点对升力系数和俯仰力矩系数的影响量近似线性地增加,但总的影响量在允许的误差范围之内,标记点对阻力系数的影响很小,可以忽略,与翼型的分析结果相似,如图8(b)。
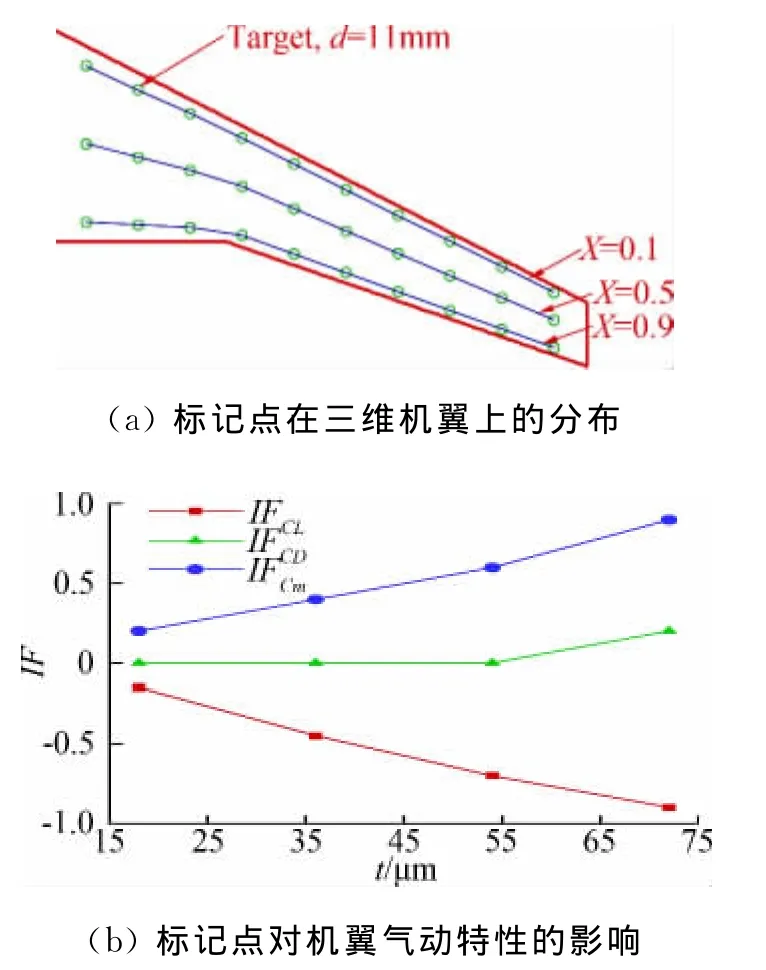
图8 标记点对三维机翼气动特性的影响Fig.8 Targets influence on aerodynamic characteristics of three dimensional wing
4 结 论
采用CFD方法对三个不同Case条件下标记点对翼型RAE2822的气动力系数影响进行了研究,获得了跨声速风洞模型变形测量实验中标记点影响的主要规律:
(1)标记点对翼型气动力系数影响因子IF随标记点的厚度t、标记点在模型上的位置X和翼型的姿态角α变化较大,且在翼型的某些位置,标记点厚度对模型气动特性的影响量随厚度的增加非线性增长。
(2)对于跨声速超临界翼型,当来流迎角为正值时,除翼型后缘附近位置,翼型上表面比下表面对标记点更敏感一些,标记点对气动力的影响量也更大一些,而模型风洞实验中,迎角运行范围中大部分是正向迎角。因此,在进行风洞模型变形视频测量实验时,将标记点粘贴在模型机翼的下表面可以有效降低标记点对模型气动特性的影响。
(3)当标记点沿展向分布数量比较少时,常规厚度的标记点对全机气动特性的影响量是可以忽略的,而当展向分布标记点数量比较多时,就需要评估标记点对全机气动特性影响量的大小。
[1]张征宇,喻波,罗川,等.2.4m跨声速风洞的模型位移视频测量精度研究[J].实验流体力学,2011,25(4):79-82.
[2]JAMES H B,ALPHEUS W B.Data fusion in wind tunnel testing;combined pressure paint and model deformation measurements(Invited)[A].20th Advanced Measurement&Ground Testing Meeting[C].Albuquerque,NM,1998.
[3]孙岩,张征宇,黄诗捷,等.风洞试验中模型迎角视觉测量技术研究[J].航空学报,2013,34(1):1-7.
[4]孙岩,姚海艳,张征宇.单相机迎角测量中振动影响研究[J].航空学报,2013,34(3):525-532.
[5]张征宇,喻波,黄诗捷,等.风洞试验中模型迎角的视频测量及精度研究[J].实验流体力学,2013,27(1):88-92.
[6]孙岩,张征宇,邓小刚,等.风洞模型静弹性变形对气动力影响研究[J].空气动力学学报,2013,31(3):294-300.
[7]ALBERTANI R,STANFORD B,HUBNER J P,et al.Aerodynamic coefficients and deformation measurements on flexible micro air vehicle wings[J].ExperimentalMechanics,2007,47:625-635.
[8]NATHAN A P,JONATHAN T B,MARK F R,et al.Videogrammetry dynamics measurements of a lightweight flexible wing in a wind tunnel[A].50th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference[C].Palm Springs,California,2009.
[9]孙岩,张征宇,吕彬彬,等.T型尾翼颤振光学测量实验与弯扭特性解算[J].实验流体力学,2012,26(1):100-104.
[10]恽起麟.风洞实验数据的误差与修正[M].北京:国防工业出版社,1996.
[11]罗川,张征宇,孙岩,等.模型变形视频测量的相机位置坐标与姿态角确定[J].实验流体力学,2010,24(6):88-91.
[12]ALPHEUS W B,LIU T S,GARG S,et al.Unified model deformation and flow transition measurements[J].JournalofAircraft,1999,36(5):898-901.
[13]ALPHEUS W B,LIU T S.Videogrammetric model deformation measurement technique[J].JournalofAircraft,2001,38(4):745-754.
[14]陶洋,范召林,吴继飞.基于CFD的方形截面导弹纵向虚拟飞行模拟[J].力学学报,2010,42(2):169-177.
[15]COOK P H,MCDONALD M A,FIRMIN M C P.Aerofoil RAE2822pressure distributions,and boundary layer and wake measurements:experimental data base for computer program assessment[R].AGARD Report AR 138,1979.
[16]周璇,李水乡,陈斌.非结构动网格生成的弹簧-插值联合方法[J].航空学报,2010,31(7):1389-1395.
