模块化四轮全向驱动小车设计与运动控制方法

2013-11-08郑圣子

天津科技大学学报 2013年5期

郑圣子

(天津科技大学机械工程学院，天津 300222)

移动机器人是机器人领域的一个重要分支.在20 世纪60年代初期，学者已经开始了对移动机器人的研究[1–2].初期的研究主要集中于野外机器人的系统设计和信息处理，及其怎样构建实验系统以对新理论进行验证.近年来，对移动机器人的研究开始进入与人类生活息息相关的领域[3].移动机器人的模块化设计是当今移动机器人领域一个新的研究热点，它能大大降低研究和开发的费用，降低移动机器人成本，提供标准的零部件设计[4–5].但大多数小型机器人的模块化设计只是适用某类特定的机器人产品和硬件模块化，没有真正实现软件与硬件产品同时在不同机器人产品上的通用化.

因为全向驱动控制的显著优点，使其成为移动机器人领域的另一个研究热点.这项技术可使机器人能越过更多障碍，更加灵活和智能化[6–7].全向驱动的缺点是后续的运动学模型相对复杂.对于小型廉价机器人，宜采用单片机控制.单片机控制系统价格低，但计算能力差，能否实现对全向驱动的实时控制是机器人模块化设计的瓶颈.

本文设计了一种四轮全向驱动机器人，其采用通用接口和模块化的设计方法.针对设计提出一种模块化四轮全向驱动运动学模型，并对模型进行了分析和简化.模型通过不断地改变曲率半径实现对小车的方向控制，克服了全向驱动建模的复杂性问题.

1 四轮全向驱动机器人的模块化设计

机械结构设计是机器人运动和控制的基础.机器人与计算机相区别的一个重要特征就是机器人能够运动.要运动就必须有动力部件以及由这些动力部件驱动的结构.驱动子系统、传感子系统和控制决策子系统是一个机器人最基本的3 部分.

如图1所示，模块化设计的四轮全向驱动机器人由4个电机驱动模块、4个舵机驱动模块、4个红外障碍检测传感器模块、AVR 单片机控制器以及电缆等辅助设备组成.

图1 四轮全向驱动机器人实物图Fig.1 Physical map of omni-directional 4-wheel-driving robot

2 建立运动学模型

2.1 运动学建模过程分析

运动学是对机械系统如何运行进行研究.必须了解机器人的机械行为以正确地设计特定任务的移动机器人，即必须建立相应的运动学模型，这是移动机器人运动学最根本的问题.

建立模型是一个由底向上的过程[8].各单个轮子对机器人的运动作贡献，同时又对机器人的运动施加约束.根据小车底盘的几何特性，4个轮子是连在一起的，所以它们的约束联合起来，形成对机器人底盘的整个运动约束.在整个分析过程中，把机器人建模成轮子上的刚体，运行在水平面上.

为确定机器人的位置，建立全局坐标系和机器人局部坐标系之间的关系，见图2.坐标轴XI和YI将平面上任意一个惯性基定义为从某原点O(XI，YI)开始的全局坐标系.选择机器人的底盘中心点P 作为参考点.基于(XR，YR)定义了机器人底盘相对于P 的两个轴，从而定义了机器人的局部坐标系.在全局坐标系中，P 的位置由坐标x 和y 确定，全局和局部坐标之间的角度由θ 给定.可以将机器人的姿态描述为具有3个元素的向量：

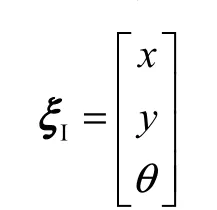
下标I 表明该姿态基于全局坐标系.为了根据分量的移动描述机器人的移动，就需要把在全局坐标系的运动映射成在机器人局部坐标系的运动.映射的是机器人当前位置的函数，该映射可用正交旋转矩阵表示：

可以用该矩阵将全局坐标系(XI，YI)中的运动映射到局部坐标系(XR，YR)中.这个运算由标记：

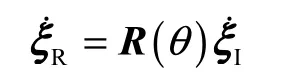
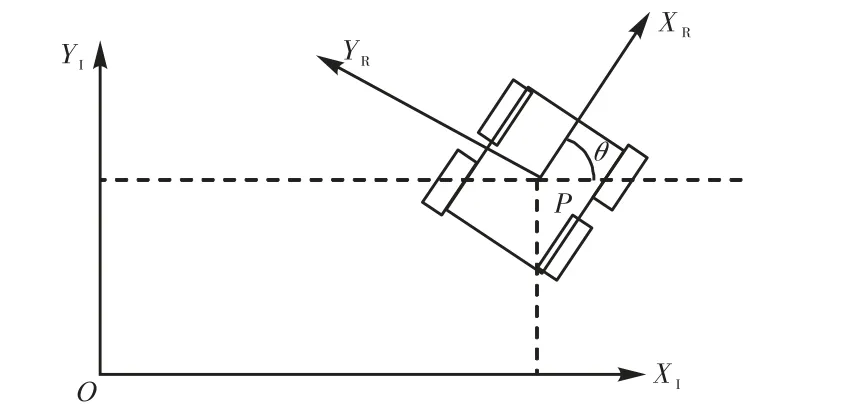
图2 建模分析示意图Fig.2 Schematic diagram of modeling analysis

2.2 轮子运动学约束

建立机器人运动学模型的第一步是表达加在单独轮子上的约束.为了简化问题便于分析，假定轮子平面总是保持垂直，且在所有的情况下，轮子与地面之间只有一个单独的接触点.

在这些条件下，每一个轮子有两个约束：第一个约束坚持滚动接触的概念，即当运动在适当方向发生时，轮子必须滚动；第二个约束坚持无横向滑动的概念，即在正交于轮子的平面，轮子必须无滑动.

小车轮子类型属于小脚轮，轮子的接触点在位置B，它被固定长度d 的刚性杆AB 连接到点A，从而固定了垂直轴的位置，B 围绕该轴进行转动.车轮有两个随时间改变的参数，φ(t)表示车轮随时间的转动，β(t)表示AB 随时间的转动角度和方向，其分析示意图见图3.

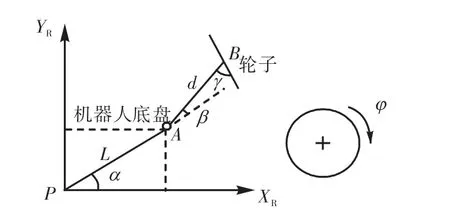
图3 小车轮分析示意图Fig.3 Schematic diagram of wheel analysis

对小脚轮而言，在与轮子平面一致的运动期间，轴偏移不起作用，其滚动约束方程为

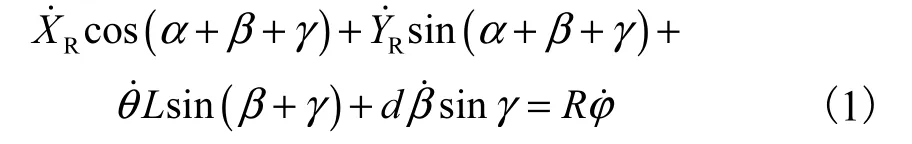
然而，小脚轮的几何特性对滑动约束有重大影响.关键问题是，在点A 发生对轮子的横向力，因为这是轮子与底盘的接触点.由于相对于点A 的地面偏移接触点，横向运动约束不为零，此约束是一个滚动约束.因此，必定产生垂直于轴的适当转动：

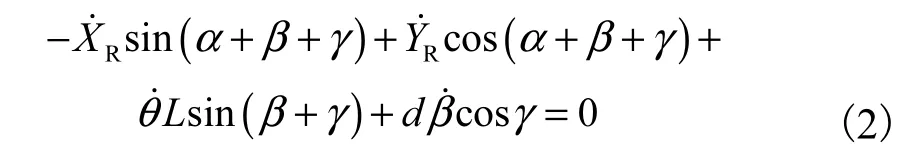
式(1)、式(2)是一个轮子的运动方程，将4个轮子的方程联立即为小车的运动模型.

2.3 运动学模型的简化

2.3.1 模型的简化理论

上述运动模型是四轮小车机器人的通用模型，对于小车要走的路径、前进的方向，可以有多种选择，模型有多种解，实现方法多样.为便于计算和编程，实现不同的路径轨迹，必须对模型进行简化.

任何一条曲线都可看作是由无数曲率半径已知的小圆弧组成的，这是对模型进行简化的基础.由于每个小车轮子都配有舵机，每个轮子都能灵活运动，故可以按曲率半径来控制小车的运动轨迹.转弯时小车4个车轮的法线相交于路径曲线的曲率中心.

2.3.2 模型简化的实现

以图4中小车向右转为例进行详细分析，并计算小车舵机的转角，其分析过程如图5 所示.图5 中，A点为小车底盘中心(局部坐标的原点)，B 点为路径曲线曲率中心，C 点为舵机转轴，D 点为小车车轮中心，AB 为路径曲线的曲率半径，记为R，AC 为小车局部坐标原点与舵机转轴中心的距离，BD 方向为车轮法线方向.其中AB＝92,mm，CD＝75,mm，车轮半径r＝30,mm，∠BAC＝49°，轮子与CD 舵机连杆方向的夹角∠CDF＝53°.

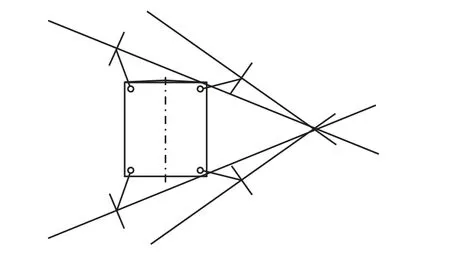
图4 小车运行示意图Fig.4 Schematic diagram of robot motion

图5 舵机转角计算分析图Fig.5 Computing analysis of motor rotation angle

在△ABC 中，∠BCA 为已知.由上述条件，利用余弦定理和正弦定理可求得BC 长度和∠ABC：

在△BCD 中，已经求得BC 的长度，BD 垂直于车轮EF，∠CDF 已知.由上述条件，利用余弦定理和正弦定理可求得BD 的长度和∠BCD：

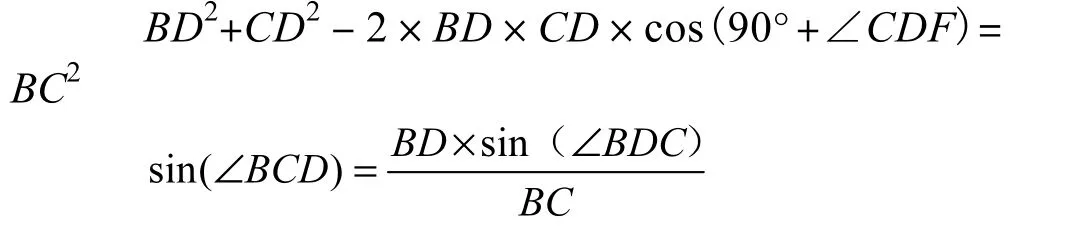
舵机连杆初始位置的方向为AC，由几何关系可以计算∠DCG，即为曲线此点位置处小车舵机的转角：

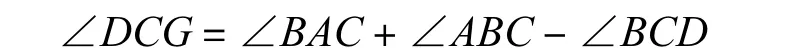
对于远离曲率中心的小车外侧轮子，其计算方法与上述计算过程类似.

由于小车几何结构和路径实现方法的特点，虽然左右两侧舵机转角大小不同，但小车同侧的舵机具有相同的转角，只是前后舵机转角的符号相反，故利用上述分析结果即可得到同侧舵机的转角.

由数学知识，任意曲线的曲率半径为

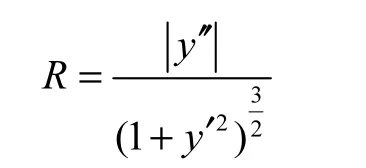
给定了机器人小车的路径曲线，就可根据上式求得曲线任意点处的曲率半径.根据求得的曲率半径就可实现设定的机器人小车路径.

2.3.3 模型简化中要解决的问题

(1)转弯问题：平面坐标系中的曲线有凹、凸两种，曲率中心可能落在平面曲线的两侧(见图6)，每一种小车具有相反的转向趋势，这就提出了小车如何转向的问题.

函数f(x)在区间I 上连续，如果对I 上任意两点x1、x2，恒有，则函数为凹函数，如果恒有，则函数为凸函数.

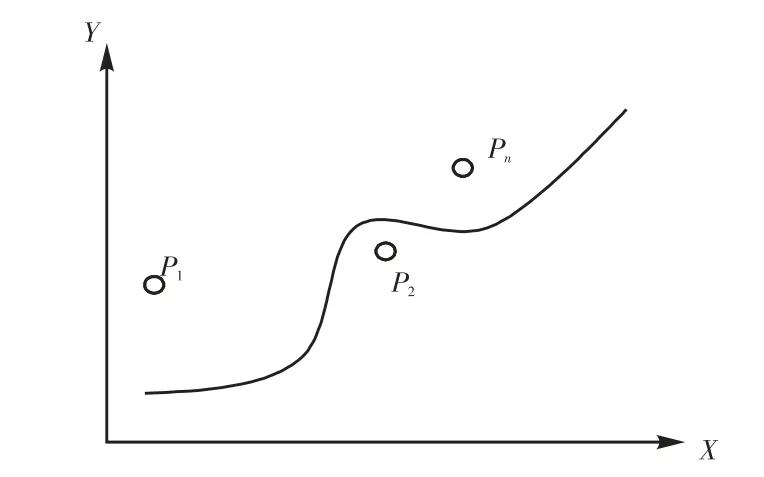
图6 曲率分析示意图Fig.6 Schematic diagram of curvature analysis

如果没有这样的限制，小车将只有一个方向的运动趋势.默认函数为凸函数时小车有向左的运动趋势，函数为凹函数时小车有向右的运动趋势，这样小车转弯的问题就解决了.

(2)曲率半径过小或过大：由于受到小车几何结构和舵机架安装的限制，舵机转角并不能随意设定，转角范围有所限制.

当曲线某处曲率半径过小时，令舵机按允许的最大转角运动，确保小车的安全，防止舵机被卡死，烧坏舵机.即小车有一最小曲率半径，当程序计算的曲率半径小于此最小曲率半径时，小车按最小曲率半径运动.

当曲线某处曲率半径过大时，由2.3.2 内容计算得来的舵机转角较小，甚至为零，可设定当曲率半径大于某一值时，默认小车沿直线前进.

3 实验

机器人机体采用ABS 塑料连接件，其质量小于2,kg.微控制器采用Atmega128 单片机，驱动电机为17,W直流电机，型号为FAULHABER 2342L012,CR，连接 47∶1 的行星齿轮减速器，舵机采用的是SolidMotion CDS5401 型数字化舵机.假定室内清扫机器人在没有障碍的情况下要求覆盖所有地面以完成清洁工作，因此本实验设定的轨迹是从一点出发不断向外扩张的螺旋线，使得清洁机器人能覆盖全部工作区域.理论轨迹和实际实验轨迹如图7 所示.

经过10 次实验，模块化机器人达到如下指标：最大前进速度12,cm/s；舵机最大转角36°；红外传感器最大探测距离2,cm.通过测量，实际轨迹与理论轨迹相的最大偏差是2,cm，机器人每步运行的反应时间小于0.05,s.而常规轨迹控制方法采用三角函数和微分运算，采用单片机控制系统的每步运算时间大于0.1,s，行走轨迹是断断续续的，不能实现实时控制.与常规轨迹控制方法的对比表明，在现有微控制器的运算速度条件下，简化的运动学模型可以实现实时控制.因此，在没有光电编码器的情况下，利用简化的运动学模型进行实时控制相对比较理想，达到了设计要求.