液压支架双伸缩立柱优化设计

2013-11-07侯康伟

河南科技 2013年18期

侯康伟

（郑州四维机电设备制造有限公司，河南郑州 450000）

液压支架最为重要的组成部件就是液压支架立柱，因为液压支架立柱自身独特的性能，可以对支架的性能和可靠性产生直接的影响，对整个的综采工作面的安全和生产效率都有直接的影响。想要对液压支架双伸缩立柱进行优化设计，就需要对双伸缩立柱进行基础性理论的研究，进而对其安全系数进行研究。

1 双伸缩立柱设计参数

在对液压支架双伸缩立柱进行内部结构的分析中，可以知道，液压支架双伸缩立柱内部结构包括有大缸活塞、中缸活塞、大缸活塞杆及立柱等。其中，假设R 为大缸的活塞直径，大缸活塞腔的工作压力为P，中缸活塞直径为r，δ 为中缸缸筒壁的厚度，p 为中缸活塞腔的工作压力，大缸的活塞杆径为d，F为立柱所能够承受的负载力。

2 双伸缩立柱设计的数学推导

假设有外负载力对立柱进行施加时，大缸和中缸就会受到相应的载荷力，而对其载荷力进行计算时，可以采用一定的公式进行，即：即：

在现实情况中，大缸缸径通常都是由相关的专业人员通过经验进行确定的，也就是D 的确定；而对于大缸的工作压力P 来说，则可以通过上述式（1）进行计算得出。而在对中缸进行缸筒壁厚度进行时，也有相应的公式可以运用，即：

通过上述式（1）和式（2）可以对大缸杆径进行公式的推导，即双伸缩立柱的大缸杆径D 的求解公式为：

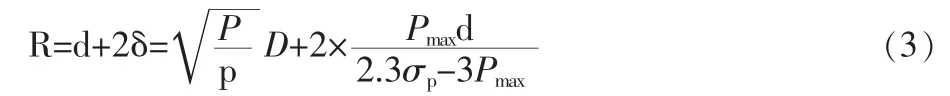
在对公式（3）进行相应的研究可以知道，大缸的杆径R 与中缸的压力p 之间具有相应的关系，而大缸杆径R 同时还与安全系数n 存在一定的关系。我们假设中缸的压力p 为自变量，而大缸杆径D 为因变量，然后对安全系数n 进行不同数值的选取，则可以得出相应的结果，然后对得出的结果进行仿真计算，可以得出一定的结论，即：第一，大缸杆径的变化会随着中缸压力的变化而变化，其变化的轨迹一般为先减小后增加，也就是说，大缸杆径在变化中存在一个最小值。第二，当两个或两个以上的中缸处于相同的压力下时，大缸的杆径会随着安全系数的变化而变化，其两者的关系为正比例关系。第三，当安全系数不断的增大时，大缸杆径的最小值所对应的中缸压力也会变小。

3 液压支架双伸缩立柱优化设计

3.1 优化模型

因为大缸杆径R 与中缸压力p 之间存在有一个极小值，且该极小值所对应的中缸压力p 与安全系数之间也具有一定的关系，所以，在进行设计的过程中，就可以用最少的材料来对双伸缩立柱进行优化设计，而进行优化设计的数学模型为：

假设对安全系数n 的选择在合适的范围内，则可以求得大缸杆径R 的最小值，同时，还可以对中缸的密封性进行保证，而所求得的最小值所对应的中缸压力p 的取值应为75—100MPa 之间。

3.2 设计实例

在下面案例中对某液压支架立柱设计进行分析，其中，该液压支架立柱的泵站压力为31.5MPa，单根立柱额定工作阻力设为3000kN。其大缸的缸径为320mm，大缸活塞腔的工作压力，而中缸的压力则需要在75—100MPa 之间进行取值，安全系数n 的取值范围为1.5—3。则对上述的参数进行输入计算之后，可以得出相关数据如下表。