剖析等价无穷小代换求解极限运算

杨春芝

（铁岭市师范高等专科学校，辽宁 铁岭 112001）

无穷小在数学理论研究上和实际工程应用中都具有重要作用，特别是在极限运算中具有独特的优势。正确合理的运用等价无穷小代换，会给极限求解带来极大的方便，甚至能够完成诺必达法则不能完成的极限求解。

1 无穷小定义及常用等价无穷小总结

1.1 无穷小定义

设函数f（x）在x0的某一去心领域内有定义（或大于某一正数时有定义）。 如果对于任意给定的正数ε （不论它多么小），总存在正数δ（或正数X），使得对于适合不等式0＜|x-x0|＜δ（或|x|＞X）的一切x，对应的函数值f（x）都满足不等式|f（x）|＜ε，那么称函数f（x）当x→x0（或x→∞）时为无穷小。 记作（或f（x）=0）。

1.2 常用等价无穷小总结

通常所用的初等函数有这样五类： 三角函数、 反三角函数、对数函数、幂函数、指数函数，复杂方程式的求解中也为这五类初等函数的组合运算。 以下列举出这五类初等函数的无穷小代换：

在当x→0 时：

幂函数无穷小代换：（1+x）a-1～ax （a 可以取整数也可以取分数）；

指数函数无穷小代换：ex～x+1，ax～lna×x+1；

对数无穷小代换：ln（1+x）～x，loga（1+x）～x/;lna；

差的无穷小代换：1-cosx～x2/2，x-sinx～x3/6，tanx-x～x3/3，xln （1+x）～x2/2，tanx-sinx ～x3/3，x-arctanx ～x3/3，arcsinx-x ～x3/6，arcsinx-arctanx～x3/2；前面两个代换后为二次函数，后面代换为三次函数。 而且从代换的等价无穷小方程式来看，代换的方程式明显比前面未代换的方程式简单得多。

2 无穷小代换求极限运算与罗比达法则对比

使用洛必达法则进行求解极限运算， 是我们计算极限时的首选方式，而且在绝大多数情况下，确实也能够获得快而且准确的结果。 但在一些复杂的求解中，洛必达法则并不具有优势，如带有三角函数和反三角函数的加减运算，因为三角函数中sinx、cosx 的两次导数就回到了本身。 现举例说明无穷小代换求解极限运算与罗比达法则对比：

当然，这需要熟记一些等价无穷小。 需要注意的是，等价无穷小的运用往往不止一次，只要发现运用洛必达法则运算困难，则可以尝试等价无穷小代换。

3 等价无穷小代换应注意问题

根据等价无穷小的定义， 当方程式的乘积因子为无穷小时，则可利用等价无穷小进行代换。 但如果方程式中有因子为无穷小，但为加减法运算，则需要考察代换的条件是否成立。

3.1 无穷小因子处于加减法运算中

但在求解中，正确采用等价无穷小代换，则会得到：

在求解中， 因为无穷小因子tanx 是作为乘积因子出现在方程式中。

3.2 在无穷小代换中需注意趋近的值

在进行无穷小代换中需确定的是：第一，必须是无穷小；第二，必须是等价无穷小之间才能进行替换。 见下例：

在本题中，如果将用代换，导致错误的结果为1。正确计算结果应当为:

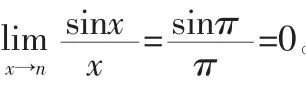
4 等价无穷小代换总结

（1）乘除运算中可以使用等价无穷小因子替换，加减运算中由于用等价无穷小替换是有条件的。 这时，满足条件则可进行代换，不满足可用泰勒公式、洛必达法则等方法来求极限。

（2）如果采用洛必达法则求导运算，在进行一次导数后，先观察一下求导后的方程式能否进行等价无穷小替换，如果能替换，则进行替换。