基于模糊综合评价法的高校内部控制有效性评估研究

王越华

(滨州学院 计划财务处， 山东 滨州 256600)

基于模糊综合评价法的高校内部控制有效性评估研究

王越华

(滨州学院 计划财务处， 山东 滨州 256600)

随着高校改革的深入，对高校内部控制有效性进行评价渐成业界热点。利用模糊综合评价法构建了高校内部控制有效性评价模型，并结合B学院的情况进行了实证分析，希望可以帮助高校提升自身的内部控制水平。

高校；内部控制；模糊综合评价法

内部控制一直是会计领域的热门话题，其运行是否有效与相关者的利益能否顺利实现密切关联。通常情况下，内部控制这一概念主要被应用于企业，如美国1997年颁布的审计准则公告第78号《财务报表审计中对内部控制的考虑：对55号的修正》就明确将内部控制界定为受企业董事会、管理当局和其他人员影响，为实现下列目标提供合理保证而设计的过程：(1)财务报告的可靠性；(2)经营的有效性和效率性；(3)相关法律、法规的遵循[1]。

随着我国教育体制改革的不断深化，高校自主权不断加大，但高校普遍运行效率低下，腐败问题层出也是不争的事实，从某种程度上讲，这正是由于内部控制失效所致[2-3]。与企业相仿，高校内部控制失效同样意味着相关者的利益受损，更甚于企业的是，因为高校提供产品的特殊性，其破坏作用通常远大于一般的企业。换言之，对高校内部控制的有效性进行评价并促其改进已成当务之急。利用模糊综合评价法评估高校内部控制有效性的文献并不多见，文献[4]简要介绍了COSO报告并对其在高校内部控制中的运用进行了初步探讨；文献[5]根据高校的实际情况初步建立了高校的内部控制评价体系。本文将运用模糊综合评价法，以“反对虚假财务委员会”(COSO)《企业风险管理——总体框架》(2004年)报告为基础，参考企业内部控制的相关经验，结合高校的实际情况构建高校内部控制有效性评价模型，尝试着评价其内部控制是否有效。

一、模糊综合评价法理论介绍

模糊综合评价法是一种基于模糊数学的综合评价方法。该方法旨在利用模糊数学的隶属度理论，在确定评价因素集、评语集和权重集的基础上，通过构造评价矩阵进行复合运算，最终确定评价对象的等级。模糊综合评价法的最大优点在于可以将模糊的、难以量化的问题通过数学语言进行描述，从而对受到多种因素制约的对象做出一个总体的定性评价。

模糊综合评价法通常按以下步骤实施：

1.确定评价因素集

评价因素是指制约评价对象的各种指标。为了确定权重集和构造评价矩阵，评价因素通常会根据其属性被分为若干不同的层次，每一层次的指标集合我们称其为因素集，本文用U表示，即评价因素集U={U1,U2,U3,…,Un}。需要特别指出的是，同层中各因素必须是相互独立的。

2.确定评语集

评语集是指评价者对评价对象可能做出的各种评价结果的集合，本文用V表示。评语集可根据实际需要确定，一般等级的划分在3级到7级之间，即评语集V={V1,V2,V3,…,Vn}(3≤n≤7)。

3.确定权重集

权重集是指构成评价因素集的各因素的重要程度，本文用W表示。为了计算的客观性，我们通常使用层次分析法(Analytic Hierarchy Process,AHP)确定各评价因素的权重。

4.构造模糊评价矩阵

构造模糊评价矩阵通常按以下步骤实施：

(1)根据评语集从最低层评价因素集开始赋值，赋值通常采用专家评价法；

(2)根据赋值结果列出评价结果统计表；

(3)根据评价结果统计表建立各层模糊评价矩阵R。

5.计算模糊评价集

计算模糊评价集A需要以相对应的权重集W和模糊评价矩阵R为基础，从最低层开始逐层进行模糊计算，直到最高层为止。其计算方法如(1)式所示。

Ai=Wi∘Ri

(1)

6.得出评价结果

最终评价结果按以下步骤得出：

(1)根据评语集V划分等级并用一组适当的数字表示；

(2)以评语集V为基础，以模糊评价集A为权重,经加权求和计算得出评价值P；

(3)找出评价值对应的等级范围，得出最终评价结果。

二、基于模糊综合评价法的高校内部控制有效性评估

(一)确定高校内部控制有效性评价因素集

根据美国反对虚假财务委员会(COSO)2004年10月颁布的《企业风险管理——总体框架》，企业内部控制因素被划分为内部环境、目标设定、事项识别、风险评估、风险反应、控制活动、信息交流与沟通、监督8个指标。以COSO报告为基础，结合高校实际情况，确定高校内部控制有效性评价因素集，如表1所示。

表1 高校内部控制有效性评价因素集分层汇总表

注：鉴于COSO报告中目标设定、事项识别、风险评估、风险反应四项因素均与风险直接相关，本文将其合并为风险文化作为第一层评价因素，将这四项因素作为其第二层评价因素。

(二)确定高校内部控制有效性评语集

本评估以判断高校内部控制是否有效为根本目的，可以据此将评语集由高到低设定为V={完全有效，较有效，基本有效，一般，基本无效，无效}。

(三)确定权重集

1.明确比率指标体系

所谓的比率指标体系事实上是对各个因素之间的重要性关系进行量化，也就是A因素和B因素的重要性之比。我们将运用9等级指标体系，具体如表2所示。

表2 比率指标体系表

注：相邻的判断取中间值2，4，6，8

2.构造判断矩阵，计算每一因素的权重Wi

判断矩阵是因素A和因素B相对于目标的重要性，其权重的计算方法如(2)式所示。

(2)

在(2)式中，Xi为判断矩阵每一行标度值乘积的N次方根，N为判断矩阵的阶数。需要指出的是，当Ngt;2时，还需要进行一致性检验，确保一致性指标CRlt;0.1。

根据高校内部控制有效性评价因素集分层汇总表，通过咨询高校财务领域的专家，我们可以构造如下6个判断矩阵并计算其相应权重，具体见表3～表8。

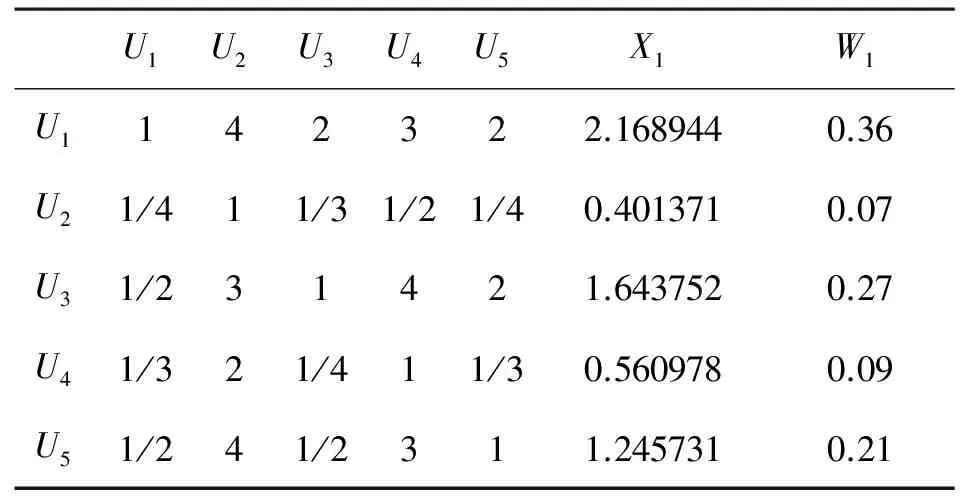
表3 高校内部控制有效性评估一级指标判断矩阵

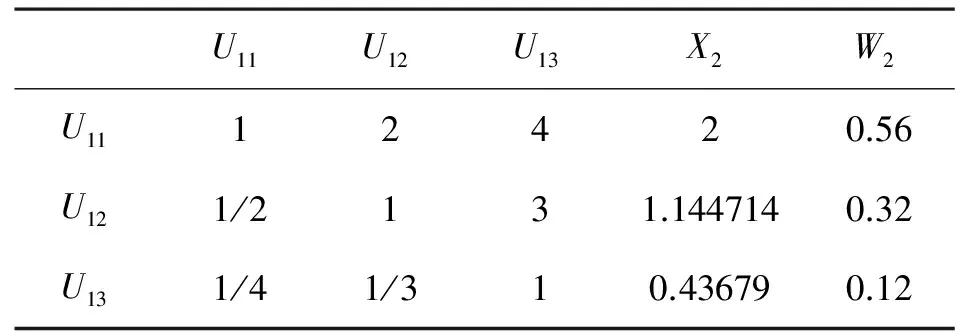
表4 内部环境有效性评估二级指标判断矩阵

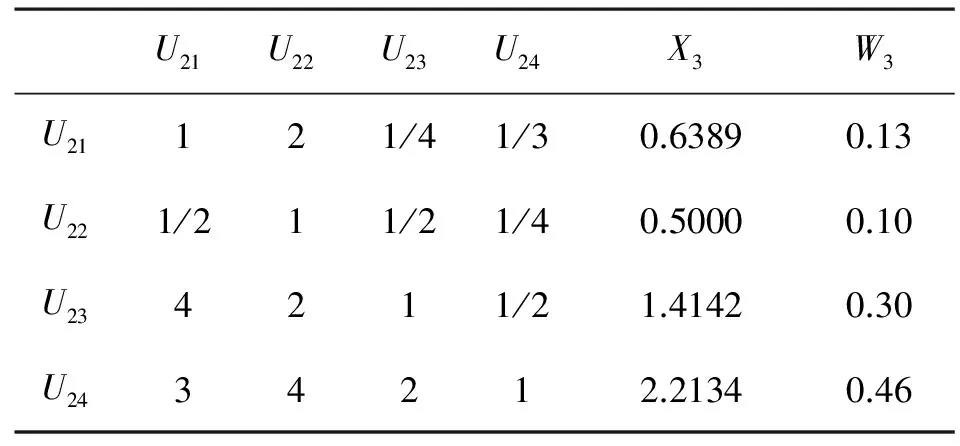
表5 风险文化有效性评估二级指标判断矩阵

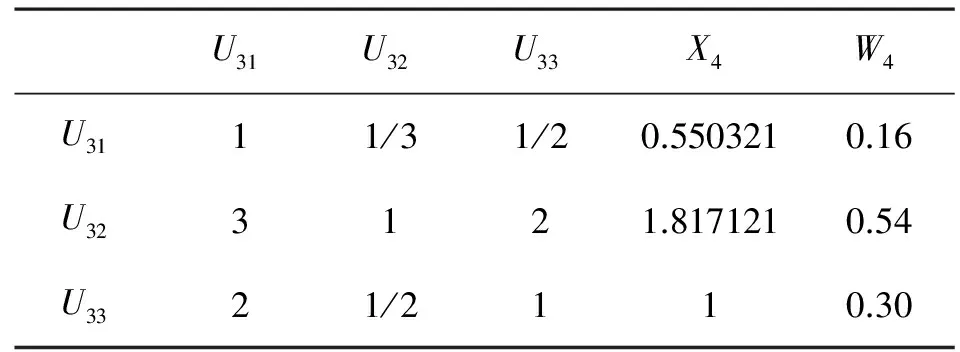
表6 控制活动有效性评估二级指标判断矩阵

表7 信息与沟通有效性评估二级指标判断矩阵

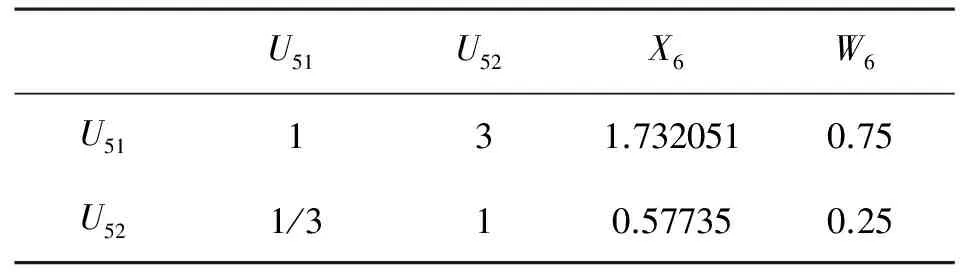
表8 监督有效性评估二级指标判断矩阵

因为二阶矩阵不需要进行一致性检验，因而只需要对其他5个矩阵进行一致性检验即可。利用相关数学方法[6]可以求出5个矩阵的最大特征根分别为λ1=5.2、λ2=3.02、λ3=4.2、λ4=3.01、λ5=3.05。以此为基础，可以求出5个矩阵的一致性指标CR分别为CR1=0.045、CR2=0.016、CR3=0.073、CR4=0.008、CR5=0.046。因为当CR﹤0.1时，矩阵满足一致性需要，所以我们可以判断上述5个判断矩阵符合一致性要求。由此可以得出6个权重集，即W1=(0.36，0.07，0.27，0.09，0.21)、W2=(0.56，0.32，0.12)、W3=(0.13,0.1,0.3,0.46) 、W4=(0.16，0.54，0.3)、W5=(0.53，0.33，0.14)、W6=(0.75，0.25)。

(四)构造模糊评价矩阵

构造模糊评价矩阵首先需要专家从最低层次评价因素集开始赋值。以评价因素集U1为例，假定有10位专家评价，依据评语集V,可分别得出因素U11、U12、U13的评价结果，详见表9。

表9 评价结果统计表

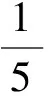
(五)计算模糊评价集

根据(1)式可得出模糊评价集A1为：

A1=W2∘R1

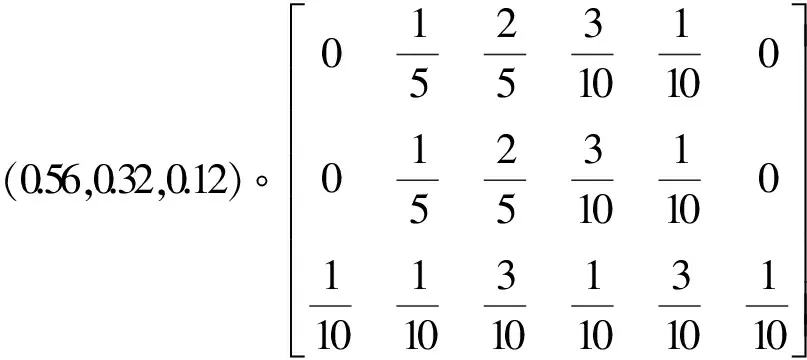
=(0.012,0.188,0.388,0.276,0.124,0.012)

(3)

(六)得出评价结果

依据评语集V={完全有效，较有效，基本有效，一般，基本无效，无效}，可以将其量化为V=(100,80,60,40,20,0)。

为了更直观地评价高校内部控制的有效性，我们还需要建立一个等级评定体系来明确其位置。结合评语集V的量化标准，我们将等级评定体系定为五级，具体如表10所示。

表10 高校内部控制有效性等级评价体系

以因素集U1为例,经计算可得出评价值P1为：

P1=A1×VT

=100×0.012+80×0.188+60×0.388+

40×0.276+20×0.124+0×0.012

=53.04

(4)

对应表10的评价体系，可以发现P1处于“一般”区间，即“内部环境”总体一般。同理，可求出其他因素集的评价值并最终得出高校内部控制有效性的具体等级。

三、运用模糊综合评价法评价高校内部控制有效性举例

接下来，本文以B学院为例，运用模糊综合评价法评价该高校内部控制有效性。

利用高校内部控制有效性评价因素集，请熟悉B学院情况的10位专家从最低层次评价因素集开始评价，评价结果如表11所示。

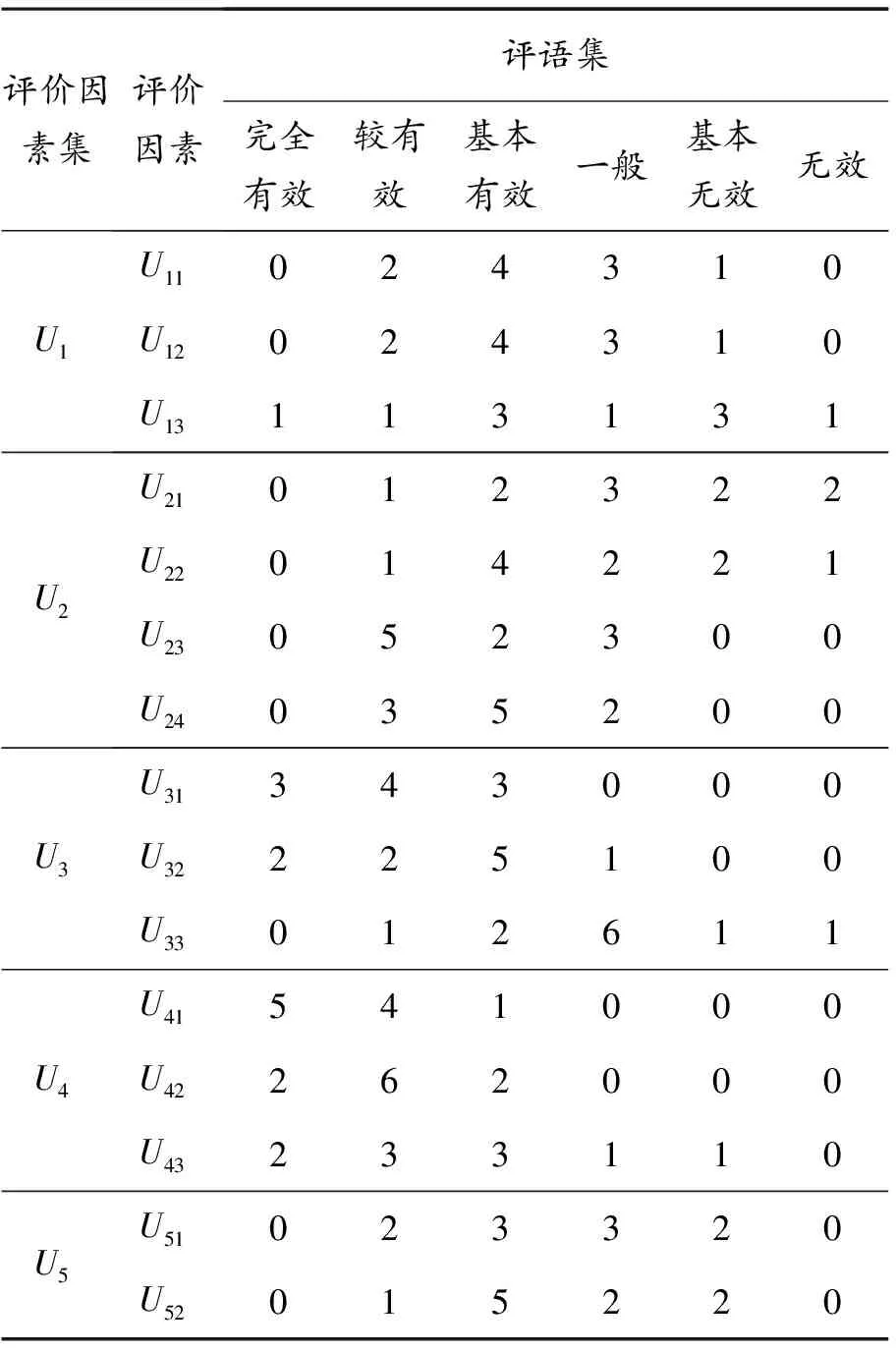
表11 B学院内部控制有效性评价结果统计表

根据表11，依据隶属度原理，可以得出基于因素集U1、U2、U3、U4、U5的模糊评价矩阵R1、R2、R3、R4、R5，具体如下：

依据权重集Wi和模糊评价矩阵Ri可求出相应的模糊评价集Ai，具体如(5)～(9)式所示：

A1W2∘R1

=(0.012,0.188,0.388,0.276,0.124,0.012)

(5)

A2=W3∘R2

=(0,0.312,0.36,0.243,0.048,0.037)

(6)

A3=W4∘R3

=(0.156,0.202,0.378,0.234,0.03,0)

(7)

A4=W5∘R4

=(0.359,0.452,0.161,0.014,0.014,0)

(8)

A5=W6∘R5

=(0,0.175,0.35,0.275,0.2,0)

(9)

依据评语集的量化标准V={完全有效，较有效，基本有效，一般，基本无效，无效}=(100，80，60，40，20，0)，可得出因素集Ui相应的评价值Pi，具体如(10)～(14)式所示：

P1=A1×VT

=100×0.012+80×0.188+60×0.388+40×0.276+20×0.124+0×0.012

=53.04

(10)

P2=A2×VT

=100×0+80×0.312+60×0.36+40×0.243+

20×0.048+0×0.037

=57.24

(11)

P3=A3×VT

=100×0.156+80×0.202+60×0.378+40×0.234+20×0.03+0×0

=64.4

(12)

P4=A4×VT

=100×.0.359+80×0.452+60×0.161+40×

0.014+20×0.014+0×0

=82.56

(13)

P5=A5×VT

=100×.0+80×0.175+60×0.35+40×0.275+

20×0.2+0×0

=50

(14)

利用高校内部控制有效性评价因素集U对应的权重集W1=(0.36，0.07，0.27，0.09，0.21)、评价值集P=(53.04，57.24，64.4，82.56，50)，可得出评价因素集U对应的评价值P，具体计算如(15)式所示：

P=W1×PT

=0.36×53.04+0.07×57.24+64.4×0.27+82.56×0.09+50×0.21

=58.45

(15)

对应表10的评价体系，可以发现B学院的内部控制有效性处于一般区间，这说明B学院在内部控制方面存在着不足，特别是在内部环境、风险文化和监督三个方面明显存在着缺陷，需要及时采取措施予以改善。

四、结语

高校内部控制是高校管理体系的重要组成部分，对其内部控制有效性进行评价是促进高校可持续发展的必然要求。本文尝试着运用模糊综合评价法评价高校内部控制有效性，希望可以帮助高校实现真正意义上的健康发展。

当然，由于作者水平有限，所以上述结论更多的是一家之言，如若有偏颇之处，希望各位专家不吝指正。同时，由于受到时间和精力方面的限制，在指标选取和权重确定上未能做到尽善尽美，希望能够在未来的日子里在这一方面进行更为深入细致的研究，得出更为令人信服的结论。

[1]陈关亭，李姝.中美内部控制评审准则比较 [J].审计研究，2002(5)：32-37.

[2]许学丹.高校内部控制存在的问题及其完善措施[J].财会通讯，2009(3)：88-89.

[3]于志云.高校内部会计控制体系分析[J].财务通讯：综合，2009(10)：94-95.

[4]张春富，张莎.COSO报告在高校内部控制中的运用[J].教育财会研究，2010，21(3)：60-62.

[5]郑萍.高校内部控制评价指标体系的构建[J].会计之友，2010(8)：108-110.

[6]叶耀军，王首军，魏磊，等.矩阵最大特征值的近似求法[J].河南农业大学学报，2001(S1)：69-71.

(责任编辑吴朝平)

StudyontheEffectiveAssessmentofUniversityInternalControlbasedontheFuzzyComprehensiveAssessment

WANG Yuehua

(DepartmentofFinancial,BinzhouCollege,Binzhou,Shangdong256500,China)

With the deepening of the university reform,the assessment of effective internal control has become a hot issue.The fuzzy comprehensive assessment was used to construct the effective assessment model of university internal control,and an empirical analysis was made combined with the B college,which will help promote the level of university internal control.

university; internal control; fuzzy comprehensive assessment

G475

A

1673-8012(2013)03-0027-06

2013-04-23

王越华(1981-)，男，山东滨州人，硕士，助理会计师，主要从事财务管理研究。