基于综合指数法的中国汽车市场综合指数模型设计

吕小峰，钱志新，张晓春，程 萌

(1.南京大学工程管理学院，江苏 南京 210093)

(2.国联证券研究所，江苏 无锡 214002)

近年来，世界汽车工业的不断发展壮大，使得汽车工业在世界经济发展中的地位越来越突出。在我国，汽车产业保持着快速稳定的发展步伐，并日益成为国民经济的重要组成部分，在拉动内需、增加就业机会、促进汽车产业链的融合等方面有着十分重要的作用。受世界经济一体化及产业转型变革的影响，汽车行业竞争越来越激烈，许多学者、行业研究员、汽车公司高管开始研究如何通过一种有效的方法简单直观地对整个汽车行业的综合发展能力进行评价，以便于更好地制定策略和预防风险。已有相关学者通过综合指数法、因子分析法和层次分析法对汽车行业相关领域问题进行评价研究。范维等(2009年)采用因子分析法，对30家汽车上市公司进行了评价分析，揭示了汽车行业企业之间经济效益差异的主要原因[1]。党林杰等(2008年)根据影响汽车企业经营的因素，并利用层次分析法建立了汽车企业绩效的综合评价模型[2]。孙世敏等(2010年)采用因子分析法对我国汽车行业30家上市公司的经营业绩进行了综合评价，并运用聚类分析法对因子分析的结果进行了分类[3]。此外还有诸多学者采用综合指数、因子分析等方法对汽车行业的其他问题进行了研究[4－6]。

本文综合前人的相关研究成果和工作实践经验，首次提出基于综合指数法的中国汽车市场综合指数模型，通过构建合理的市场指数评价指标，将因子分析法和层次分析法相结合，运用定性定量相结合方式科学合理地计算市场指数值，并最大化地贴近实际指数编制的原则和要求，从而能够简单直观地反映汽车市场的综合变化趋势和整体波动情况，对预测行业发展的周期、识别行业发展的高峰和低谷有着良好的预警效果。

1 指标体系构建

现有的关于汽车行业业绩评价指标体系基本上都是从财务分析的角度出发，将综合能力分为经营能力、盈利能力、偿债能力和成长能力等4大基本指标来分析。由于目前国家统计局对行业数据发布是按照季度形式发布的，考虑到指数发布的时效性，因此本文利用AHP的相关方法构建以资本市场、实体经济和信心指数为一级指标的综合评价体系，见表1，其涵盖了4个二级指标和18个三级指标。指数每月对外发布2次，分为上半月指数和下半月指数，综合考虑国家统计局数据延迟等因素，对指标数据选取期限做必要说明。表中标明“即时”的指标为上下半月均有数据的指标，当期指数取其当期值;标明“下半月”的指标为下半月指数调整指标，当前下半月指数取其当期数据;其余指标为上半月公布数据的指标，这些数据延期一个月，当前上半月指数取其上个月底指标数据。

2 计算模型

2.1 评价方法

本文将因子分析法和层次分析法相结合进行因子缩减、指标权重计算、指标得分计算等，实现定性计算和定量计算的有效结合，最终利用综合指数法的相关理论和方法计算指数值。当然整个计算流程的设计是基于综合指数法的相关原理，其计算模型框架如图1所示。综合指数法是指在确定一套合理的经济效益指标体系的基础上，对各项经济效益指标个体指数加权平均，计算出经济效益综合值，用以综合评价经济效益的一种方法[7]。其理论和思想与因子分析及层次分析都有许多相似之处。由于因子分析法和层次分析法都是比较成熟的数学量化方法，因此本文不再对其数学过程进行详细描述。

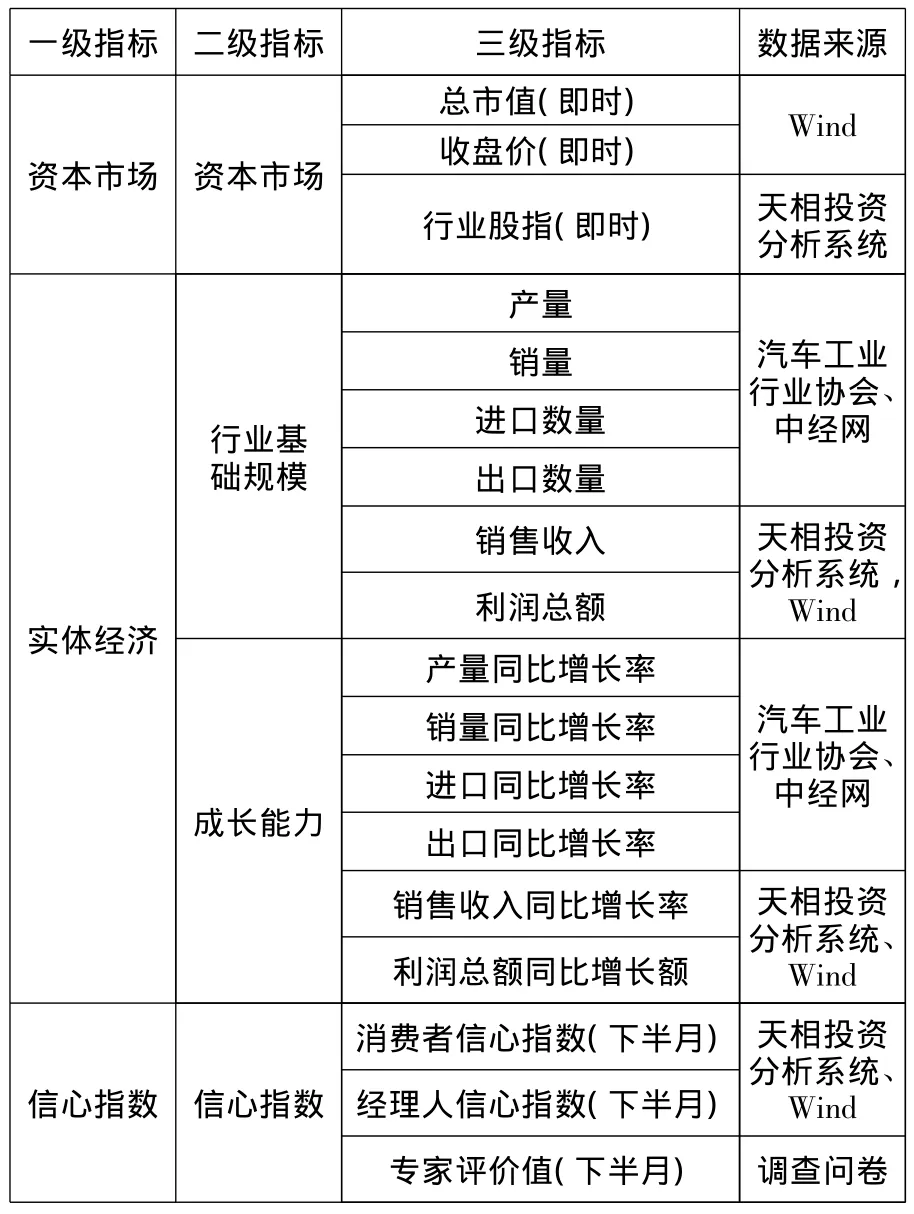
表1 中国汽车市场综合指数指标体系

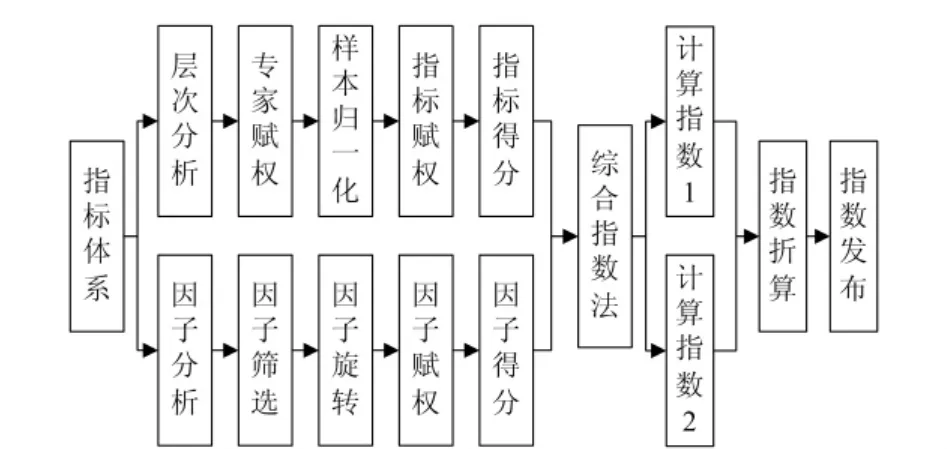
图1 中国汽车市场综合指数计算模型框架

2.2 因子分析法计算指标体系得分

从数据库中取出中国汽车市场综合指标评价体系指标的2005－1－1～2012－7－31期间的每月上半月和下半月的数据，采用SPSS软件调用因子分析法对其原始数据进行分析[8]。

a.KMO和Bartlett检验结果。

运用KMO样本测度法和Bartlett球体检验法对指标相关性及模型适用性检验。检验结果表明，KMO抽样适度测定值为0.819;同时，Bartlett球体检验的值为6529.956，自由度为153，显著性概率为0.000，表明指标之间具有较强的相关性，适用因子分析。

b.公因子提取。

采用主成分分析法求初始公因子特征值、方差贡献率及累计方差贡献率。计算结果表明，特征值大于1的成分主要有4个，表明18个指标可以综合为4个主成分，它们的累积方差贡献率是86.6%，反映了4个因子提供了原始数据的绝大部分信息，见表2。

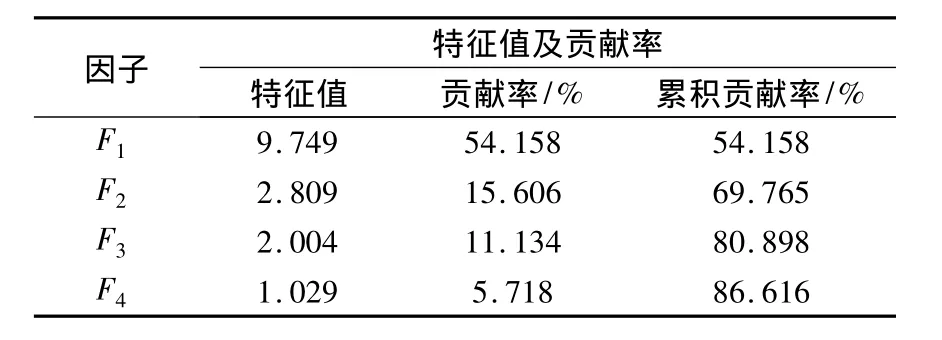
表2 因子特征值和贡献率

c.建立因子载荷矩阵，进行因子旋转，计算因子得分。

对所提取的 4个主因子 F1，F2，F3，F4建立因子载荷矩阵，为便于对各因子载荷进行合理的解释，采用正交最大方差旋转法对因子进行旋转，使每个因子的载荷的平方按列向0或1两极分化，从而得到方差最大旋转矩阵，见表3。从表中可以清晰地看出因子F1对产量、销量、进口量、出口量、销售收入、利润总额等指标有较大载荷，这些指标反映了汽车市场的总体规模;因子F2对总市值、收盘价、股指等指标有较大的载荷，反映了汽车资本市场的情况;因子F3对消费者信心指数、经理人信心指数以及专家预测评定值等指标有较大载荷，反映了整个市场的信心状况;因子F4对产销量同比增长率、进出口同比增长率、销售收入同比增长率和利润同比增长率等指标有较大载荷，综合反映了汽车市场的成长性。

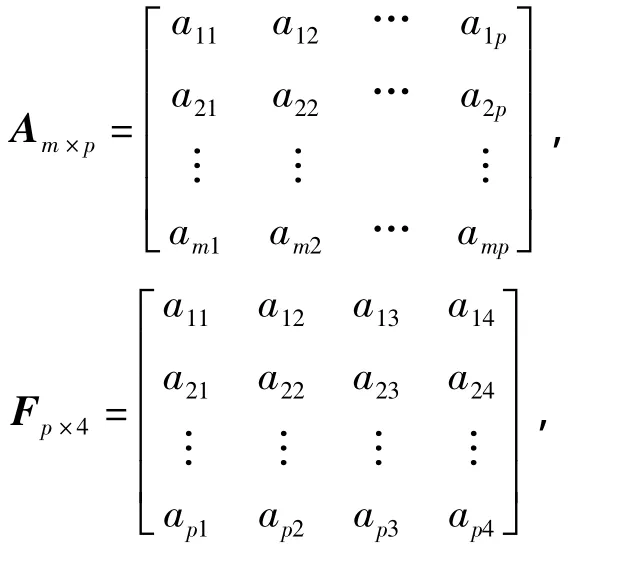
采用回归方法计算因子的得分系数，得分系数代表了该因子对每个指标的贡献度，见表3。据此可以计算每个样本的得分，并根据因子贡献率(因子权重)计算最终综合评定值E，见表4。假设样本矩阵为Am×p，因子得分系数矩阵为Fp×4，则因子得分矩阵为Sm×4，因子的综合评定值矩阵为 Em×4，则有:

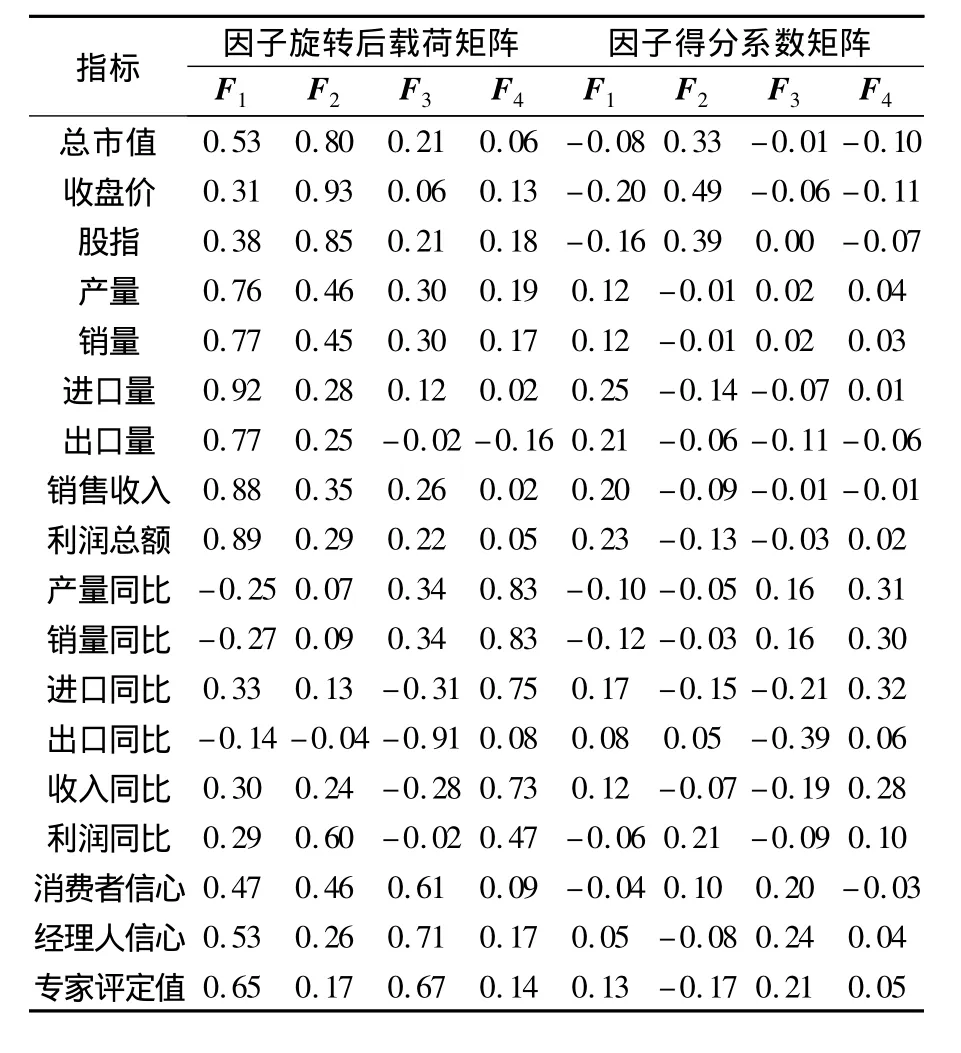
表3 因子旋转后的载荷矩阵、得分系数矩阵

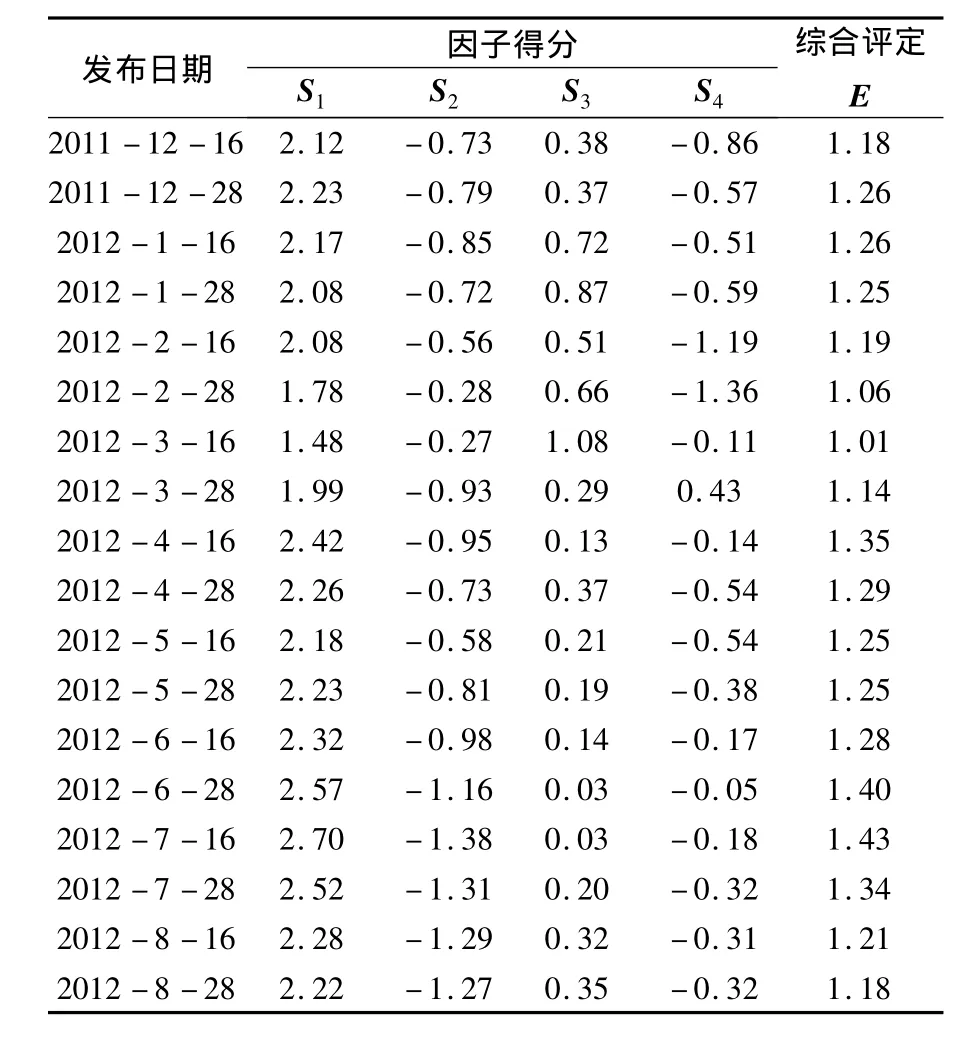
表4 因子得分和综合评定值(部分样本)

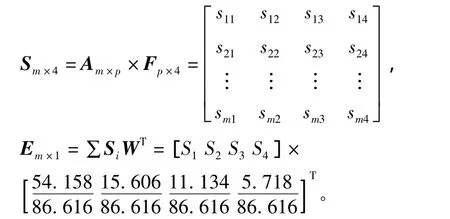
2.3 层次分析法计算指标体系得分

通过专家对各级指标相对上一级的重要性进行打分，形成判别矩阵A，计算判断矩阵A中每行所有元素的几何平均值得到W=(w1，w2，…，wn)T。将wi归一化，计算即为所求特征向量的近似值，这也是各元素的相对权重。计算判断矩阵最大特征值λmax=最后进行一致性检验，计算一致性指标CI=(λmax－1)/(n－1)，由矩阵权值表查出平均随机一致性指标RI，计算一致性比例CR=CI/RI时，当CR＜0.1，认为判断矩阵的一致性可以接受，否则要对矩阵进行调整。

在得出每个指标相对于上一级的权重后，采用加权法求出每个三级指标相对于总目标的权重W。采用正态归一化法将原始数据无量纲化处理后得到，加权求出该样本的综合评定值Gi=w1×zi1+w2×zi2+… +w18×zi18，这里和因子分析法的最后求综合值操作类似，只不过这里依然保留18个指标，而因子分析法进行了因子缩减，计算指标权重，见表5。

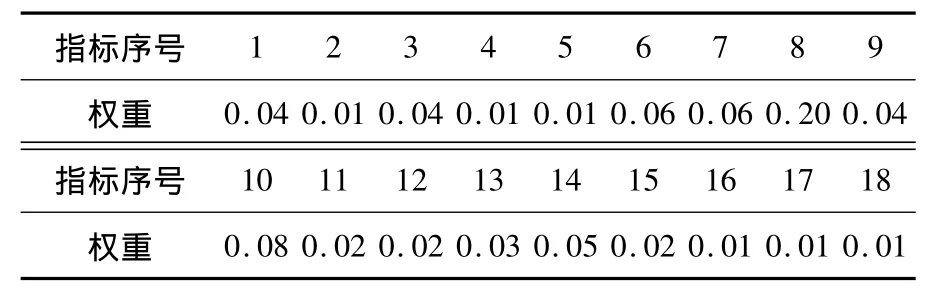
表5 层次分析法计算指标权重

2.4 综合指数计算

综合指数法计算过程主要分为以下几个步骤:

Step1:定基准序列、基期和基准值。根据实际需要，规定以2005－1－1～2009－12－31共5年120期作为基准序列，以2009－1－1为基期，设定基准值为1000。

Step2:指数折算。将基准指数折算到一定的范围内，本模型将基础序列控制在850～1100范围内，公式如下:

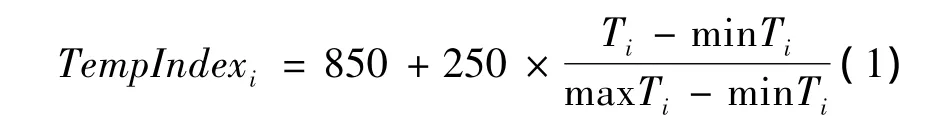
式中:TempIndexi表示折算指数值;Ti表示每期的综合得分;maxTi和minTi为当前考察序列中Ti的最大值和最小值。分别用每期的因子综合评分值Ei和层次分析评定值Gi分别代入公式(1)中计算，得到折算指数FactorIndexi和AhpIndexi，并根据基期的折算指数值大小和基准值进行折算，例如当期折算后的FactorIndexi=当期折算前的FactorIndexi+1000－基期的FactorIndex，则每期综合折算值TempIndexi=1/2 × FactorIndexi+1/2 ×AhpIndexi。

Step3:指数发布。由于每期新的数据公布，通过因子分析或是层次分析都会因数据序列的归一化而造成因子权重变化和整个折算指数序列的改变，因此考虑到指数对外发布的连续性，将调整近两期折算指数的差值，第i期的发布指数值Ii=Ii－1+TempIndexi－TempIndexi－1。

通过综合指数计算的中国汽车市场综合指数趋势图如图2所示，从图中可以看出，上下半月的指数值比较接近，下半月指数只是通过市场的信心状况对上半月指数做微调，此种方法计算出来的指数充分满足实际的工作需求，使得指数的编制和计算更加科学合理。图3是综合指数和由汽车工业协会发布的汽车行业景气指数的对比图，从图中可以看出，2009～2010年行业指数上升态势一致且明显。自2011年以来，行业指数增速趋缓，综合指数和景气指数略有差别，主要原因是本文所构建的综合指数除了包含景气指数所考察的主要指标外，对汽车进出口、股指、收盘价等指标也进行了综合评定，所以即使在2011年产销量及行业利润有所下滑的时候，由于进出口的稳定增加，行业综合指数只是增速趋缓，整体还是略有上升;此外，景气指数发布周期为1个季度，综合指数发布周期为半个月，综合指数对市场的信心指数变化也进行了充分的评价。通过历史数据回溯，综合指数较好地反映了各主要指标的变化趋势，如图4所示。以上均证明了本指数的科学性和有效性，在实际运用中能更贴近市场需求。

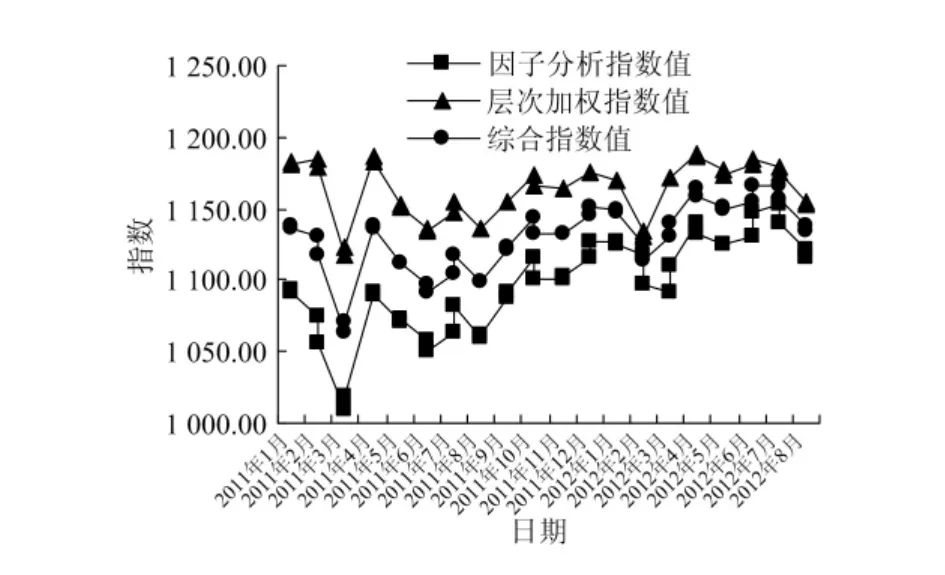
图2 综合指数趋势图(2011－2012)

图3 综合指数和景气指数对比图

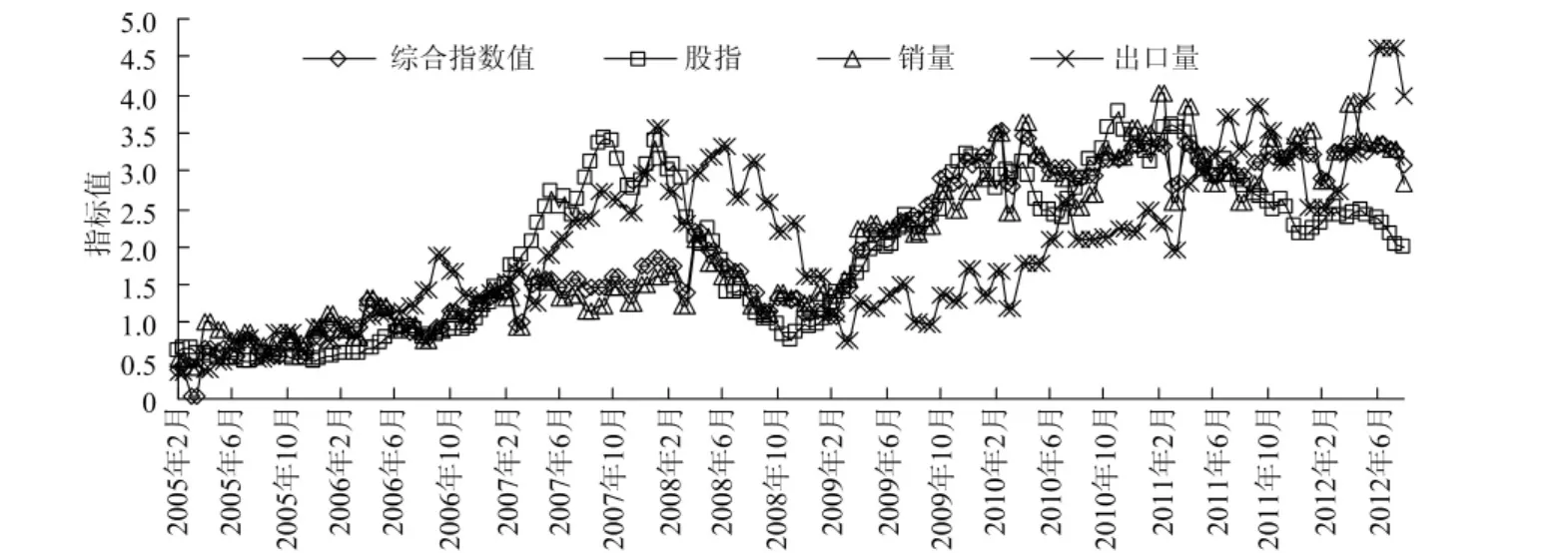
图4 综合指数和主要指标的走势对比图

3 结束语

本文有效地运用了综合指数法的相关原理和方法，对中国汽车市场综合指数模型的设计和分析过程进行了较为详细的阐述。本文的相关研究成果已在实践中得到了较好的应用和推广，中国汽车市场综合指数综合反映了汽车市场的整体发展趋势，能够简单直观地识别出行业发展的高峰期和低谷期，对政府、行业和企业的相关分析师的决策有较大的辅助作用。

[1] 范维，王新红.基于因子分析法的汽车类上市公司业绩评价[J].技术与创新管理，2009，30(2):188－190.

[2] 党林杰，聂规划，申学武.基于层次分析法的汽车企业绩效综合评价探析[J].汽车工业研究，2008(5):26－28.

[3] 孙世敏，王泽平.基于因子分析法的汽车行业业绩评价研究[J].财会通讯，2010(2):143－144.

[4] 吴熙文.基于改进的层次分析法的汽车市场销售区域价值分析[J].科学技术与工程，2009，9(1):206－208.

[5] 李治国，王钰茹.基于因子分析的我国汽车零部件企业竞争力研究[J].工业技术经济，2010，29(7):142－144.

[6] 姜飞，文毅荣.基于因子分析的汽车上市公司赢利能力评价[J].经济研究导刊，2007(7):86－88.

[7] 任建智.统计指数理论与实践[M].北京:中国物资出版社，2002.

[8] 张文彤.SPSS统计分析高级教程[M].北京:高等教育出版社，2004.