折臂式高压隔离开关平衡弹簧的设计方法
2013-11-06汤文成刘成标陈厚源戴永正
张 帆,汤文成,刘成标,陈厚源,戴永正,文 博
(1.东南大学机械工程学院,江苏 南京 211189)
(2.国网电科院江苏泰事达电气有限公司,江苏 泰州 225300)
高压隔离开关是在主断路器处于正常分闸位置时,用来断开无负荷电流的电路、隔离电源的开关设备。高压隔离开关是电力系统中使用量最大的高压开关设备,但是由于长期处于合闸状态,对其很少进行操作,因此隔离开关的设计制造没有得到足够的重视,其使用性能和质量很难得到保障[1-2]。
高压隔离开关在分合操作过程中,其重心有明显的升降,导电杆位能改变从而需要较大的操作力。随着电压等级升高,需要的操作力也越大[3-4]。只通过加载大力矩的操作机构来驱动是不合理的,需要用平衡弹簧来平衡位能的变化,从而降低操作力矩。理想平衡弹簧所产生的平衡力矩都能刚好抵消重力所产生的力矩,所以不管导电杆如何笨重,只需克服摩擦阻力就可以上升或下降。平衡弹簧在实际设计过程中很难达到理想状态,驱动机构需要输入额外的驱动力矩才能完成高压隔离开关正常开合。输入驱动力矩的大小是评价平衡弹簧设计好坏的一个重要标准。平衡弹簧设计的方法很多,本文主要从能量转换和虚拟仿真2个方面对平衡弹簧的设计进行研究。
1 能量法
1.1 建立数学分析模型
对开合闸机构建立的数学分析模型如图1所示,D点为下导电杆铰链点,E点为拉板铰链点,F点为内拉杆铰链点,O点为齿轮中心点,Q点为上导电杆顶点,M点为O点在下拉杆(也可以说是下导电管)上的投影,P点为D点在下拉杆延长线上的投影,N点为齿轮齿条的节点,ON的长度即为节圆半径,G为下导电杆的质心,H为上导电杆的质心,θ为下导电杆与水平线的夹角,β为下导电杆和上导电杆的夹角,∠GDO为质心G与D点连线和下导电杆的夹角,∠HOQ为质心H和O点连线与上导电杆的夹角。
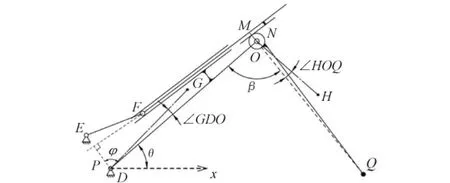
图1 开合闸机构简图
质心G和H是通过建立折臂式高压隔离开关三维实体模型求得的,即在Pro/E中设置各零件的材料信息后,通过功能Analysis得出G点相对于D点的坐标,同理求得H点相对于O点的坐标。
1.2 建立开合闸机构运动学方程
在导电臂的运动过程中,点P、D、O、N、M的相对位置不变,且角φ也为定值,由此可以首先确定机构中一些定量,如OD和φ。
图2,3分别为机构在开闸与合闸位置的状态。设定导电杆在闭合状态时下导电杆与x轴的夹角为θ',上、下导电杆之间的夹角是β';导电杆在展开位置时下导电杆与x轴的夹角是θ″,上、下导电杆之间的夹角是β″;∠QOx为上导电杆OQ与x轴的夹角。在未做特殊说明的情况下规定物理量的上标“'”表示导电杆的闭合状态,同理规定“″”表示导电杆的展开状态。
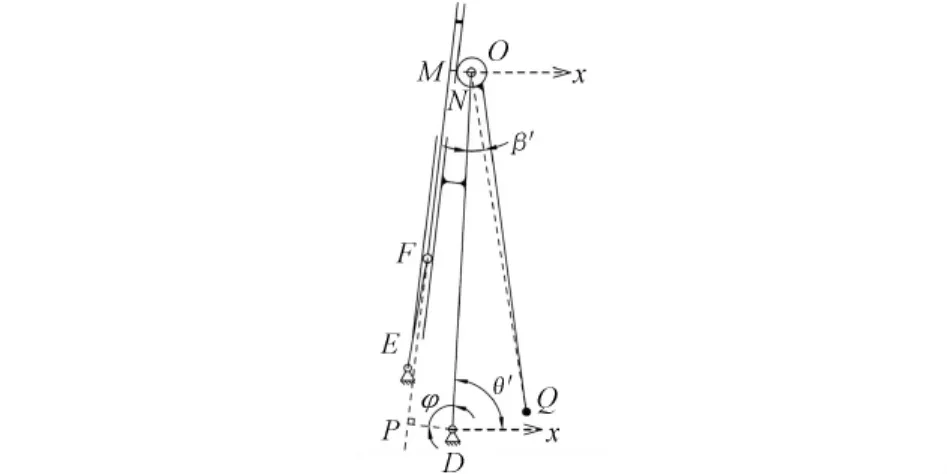
图2 开合闸机构在开闸时的位置

图3 开合闸机构在合闸时的位置
由此可以得出以下数值不随机构的运动而改变:∠QOx,θ″,β″,进一步计算点 O、M、P 的坐标。又因F点始终位于线MF上,令系数0≤u≤1,可以得到:
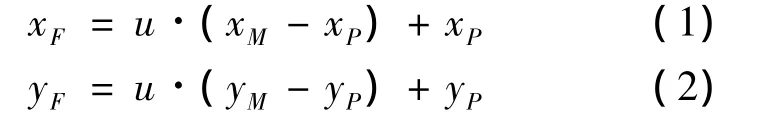
最终,可以求出运动过程中Q点的坐标,即Q点的运动轨迹:

1.3 理想平衡弹簧的计算
根据上述分析计算质心G和H点在开合闸机构运动过程中的纵坐标和在分闸位置两点的纵坐标,当隔离开关处于分闸位置时,平衡弹簧的压缩量为弹簧安装的预压缩量Δl',从而得出在机构运行中弹簧的变形量为:

上、下导电杆的质量分别为m1,m2,弹簧的刚度为k。系统重力势能和弹簧的弹性势能分别为Eg和Ek。根据理想平衡弹簧条件,且在忽略摩擦的情况下得出:
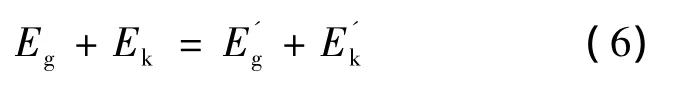

从而求得理想弹簧平衡力为进而求得理想平衡弹簧刚度值k:
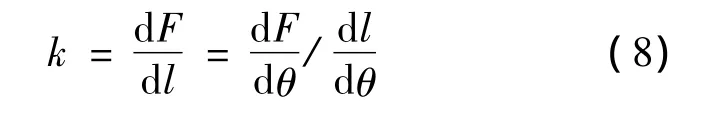
1.4 理想与实际平衡弹簧力对比
本文以江苏某企业生产的GW17型折臂式高压隔离开关为例,按上述计算得出在合闸过程中理想平衡弹簧力的大小。对现有产品的弹簧进行压缩试验,测出平衡弹簧力随压缩量变化的相关数据,测量工具和结果如图4所示。
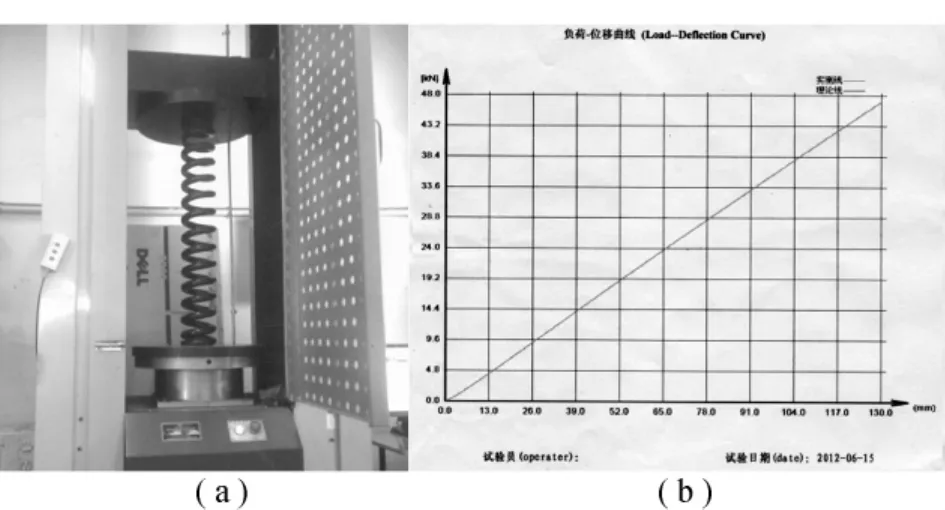
图4 实际弹簧力的检测
GW17型产品在合闸过程中(弹簧压缩)理想平衡弹簧力和实际平衡弹簧力对比如图5所示。从图中可以看出,合闸的中后期平衡弹簧提供的平衡力比理想状态下的大,理想平衡弹簧刚度先减小后增大,合闸的末期出现平衡点。

图5 GW17型产品中平衡弹簧的理想弹簧力与实际弹簧力
2 虚拟样机法
虚拟样机技术是一项新生的工程技术,它采用计算机仿真与虚拟技术,在计算机上通过CAD/CAM/CAE等技术把产品的资料集成到一个可视化的环境中,实现产品的仿真、分析。虚拟样机技术在设计的初始阶段就可以对整个系统进行完整的分析,可以观察并试验各组成部件的相互运动情况。使用仿真软件可以在各种虚拟环境中真实地模拟系统的运动,在计算机上可以方便地修改设计缺陷,仿真试验不同的设计方案,对整个系统不断改进,直至获得最优化设计方案,再做出物理样机,这样可以减少试验成本,缩短整个设计过程[5-6]。
2.1 仿真模型的建立
在ADAMS中建立的仿真模型如图6所示,模型开始位于开闸位置。模型分为8个部分,分别是:底座、拐臂、六方螺杆、下导电杆装配体、上导电杆装配体、拉板、内拉杆装配体和平衡弹簧。在ADAMS中定义的约束有:固定副、旋转副、移动副和齿轮副。
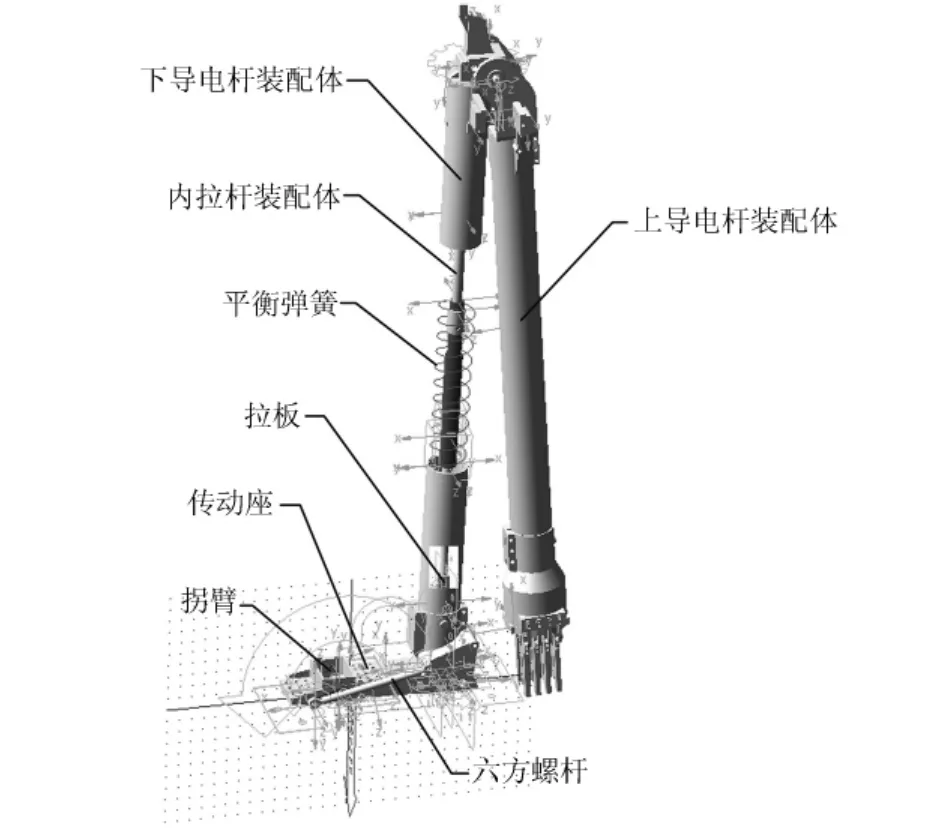
图6 GW17型高压隔离开关仿真模型
2.2 理想平衡弹簧的计算
理想平衡弹簧是为了方便对机构进行研究而进行的理想性假设,即整个机构没有摩擦,没有能量损失,平衡弹簧弹性势能的变化等于机构重力势能的变化;理想状况下,即使驱动力矩很小,机构也能够正常地完成开闸、合闸,并且机构可以稳定地停在任何位置。
首先,不考虑摩擦的影响,即开闸和合闸互为逆过程,因此只需研究合闸过程。平衡弹簧的参数包括刚度系数k、压缩量L,这些参数由机构本身的尺寸和机构的质量决定,仿真过程中可以测得内拉杆和下导电管之间的相对位移S,且S=L,测量数据如图7所示。
从图7可以看出,1.0~1.5s弹簧压缩得比较缓慢,1.5~7.0s平衡弹簧的压缩加速后减速,7.0~10s平衡弹簧的压缩逐渐减慢,直至合闸结束,平衡弹簧的最大压缩量发生在合闸位置,最大压缩量为129.6mm。
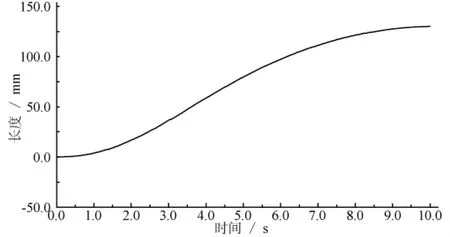
图7 平衡弹簧压缩量随时间变化图
在仿真分析中,判断弹簧是否理想的惟一标准是驱动力矩是否足够小,在不断对弹簧刚度曲线进行优化的过程中,始终关注驱动力矩的变化,一旦驱动力矩足够小,即可认为这种情况下的弹簧的刚度曲线是理想的。经过不断的修改,得到如图8所示的平衡弹簧的刚度曲线,在这种情况下,测得拐臂的驱动力矩不超过20N·m,所以认为图8所示的平衡弹簧刚度曲线是理想的。
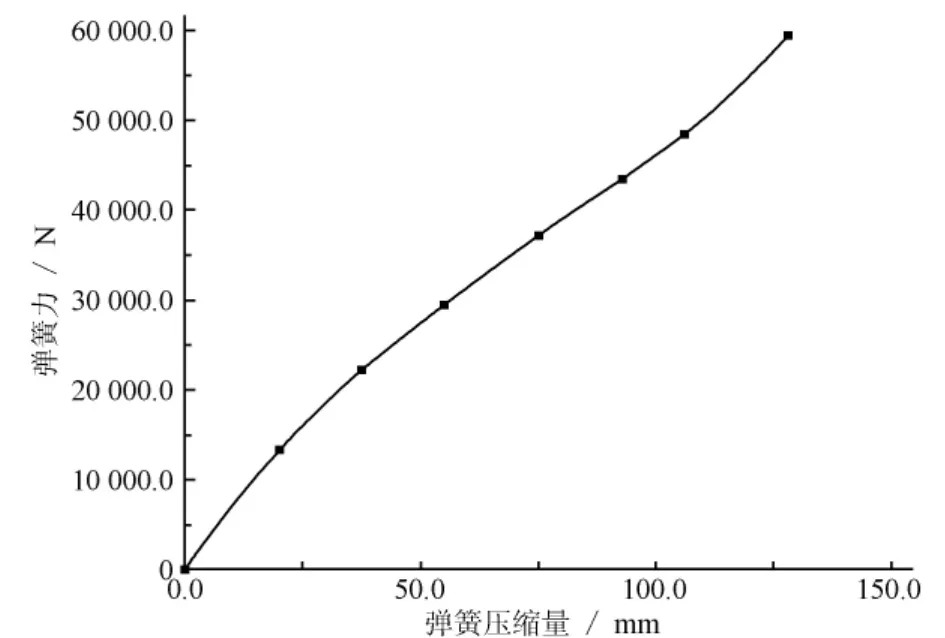
图8 理想平衡弹簧刚度曲线
2.3 理想平衡弹簧的线性化
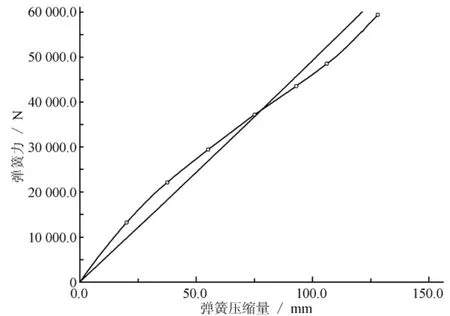
图9 线性化的理想平衡弹簧刚度曲线
实际生产制造的平衡弹簧一般属于线性,因此需要对理想平衡弹簧刚度曲线进行线性处理,如图9所示,首先估算平衡弹簧的刚度值是495N/mm,在495附近取若干离散点,分别计算驱动力矩值,最后得出在平衡弹簧刚度505 N/mm的情况下,驱动力矩的最大值最小,测得拐臂的驱动力矩最大是225N·m。
2.4 摩擦因素对平衡弹簧设计的修正
前面计算只考虑开闸或合闸一个行程,如果引入摩擦因素,则必须考虑整个开闸、合闸过程,开闸过程系统的能量变化如式(9)所示,合闸过程系统的能量变化如式(10)所示,摩擦力总是阻碍运动的发生,从式(9)、(10)中可以看出开闸和合闸不再互为逆过程,因此必须对整个开闸、合闸过程进行研究。
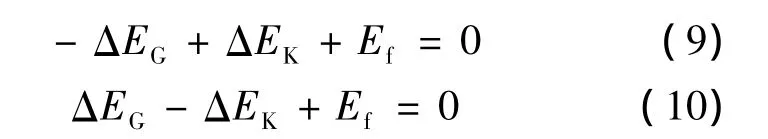
式中:ΔEG是重力势能的变化量;ΔEK是弹性势能的变化量;Ef是摩擦力在运动过程中做的功。考虑到模型的复杂性,本文只对传递力矩较大的转动副进行摩擦力的设置,在ADAMS仿真分析中设置的参数有:静态摩擦系数μs、动态摩擦系数μd、反作用力力臂等。
加入摩擦后,重新以驱动力矩为优化目标,不断地修改平衡弹簧刚度,得到平衡弹簧的刚度值是495N/mm的情况下,驱动力矩的最大值最小,拐臂的驱动力矩最大是254 N·m。
3 结束语
本文通过理论推导和虚拟样机技术的方法分别完成了高压隔离开关平衡弹簧的设计计算,结果表明,基于虚拟样机技术平衡弹簧的设计是可靠的,设计降低了对物理试验的依赖,并且避免了对机构运动学和动力学方程的推导和求解。
[1] 苑舜,崔文军.高压隔离开关设计与改造[M].北京:中国电力出版社,2007.
[2] 沈聿修.高压隔离开关、接地开关中平衡件的设置与平衡力特性的计算[J].高压电器,1995(1):14-18.
[3] 于颖.GW17型折臂式高压隔离开关传动与展开机构的分析与优化[D].南京:东南大学,2011:25-26.
[4] 邱正新,杨庆宇,梁波.水平折叠型隔离开关平衡弹簧结构优化设计[J].电气制造,2008(1):54-57.
[5] 李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2007.
[6] 范成建,熊光明,周明飞.MSC.ADAMS应用与提高[M].北京:机械工业出版社,2006:18-25.
[7] 崔吉峰.高压直流输电岗位培训教材:开关设备[M].北京:中国电力出版社,2009.
[8] 李建基.高压开关设备实用技术[M].北京:中国电力出版社,2005.
[9] 沈聿修.高压开关运动系统等效质量的计算[J].高压电器,1994(6):13-18.
[10] 文化宾.基于虚拟样机技术的新型高压真空开关研究[D].大连:大连理工大学,2009.
