基于多机理竞争退化的导弹贮存可靠性分析

罗湘勇 黄小凯

(北京航空航天大学 可靠性与系统工程学院，北京100191)

导弹具有“长期贮存、一次使用”的特点，在其全寿命周期内，绝大部分的时间是处于贮存或不工作状态，因此其贮存可靠性水平成为制约其战备完好性和应急反应能力的关键因素［1-2］.

当前，导弹贮存可靠性的研究较多地采用了加速贮存试验和自然贮存试验［3-4］.如文献［5］较全面地归纳了俄罗斯和美国自然贮存试验为主、加速贮存试验为辅的导弹贮存可靠性研究特点;文献［6-7］分别提出了导弹长期贮存条件下可靠性负增长过程的可靠度预测模型，能快速地得出导弹贮存可靠性随时间的变化规律.工程经验表明，导弹贮存可靠性是一个复杂、多机理问题，在其贮存过程中特征参数具有随机性和分散性特点，这些因素的综合考虑使得当前国内外基于单一薄弱环节和预测模型的导弹贮存可靠性研究方法具有应用局限性.

长期使用表明，远程转换开关、无线电高度表、雷达角自动装置、陀螺仪和弹上电源是影响导弹长期贮存可靠性的关键部件.首先明确导弹贮存剖面，通过定期检测得到10套导弹产品10a内各关键部件的特征电压值，然后采用移动标准偏差方法描述了各个关键部件特征电压值的贮存稳定性水平，并结合失效阈值要求得到各关键部件的贮存寿命，其次提炼出10套导弹产品的各关键部件贮存寿命，进行分布假设检验求得其贮存可靠度模型，最后根据导弹多机理竞争特点，通过仿真分析得到导弹贮存可靠性在各个贮存阶段的变化规律.本文的研究思路和结论能为长期贮存条件下贮存类产品的可靠性评估、维护方案研究提供技术支撑.

1 导弹贮存剖面分析

导弹贮存是指除“使用”之外的全部事件，即从装备交付后，到装备使用(即导弹发射飞行)或装备报废之间的整个过程，其中主要包括运输装卸、库房贮存和战备值班3个阶段［8］，典型的导弹贮存剖面如图1所示.

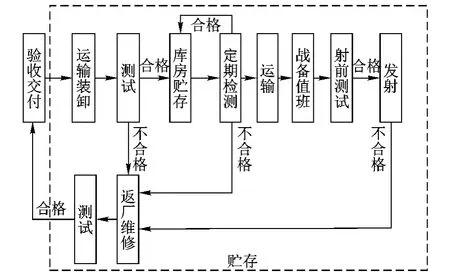
图1 典型导弹贮存剖面图

根据工程经验可得，远程转换开关、无线电高度表、雷达角自动装置、陀螺仪和弹上电源的特征电压设计标准值依次为27，-9.9，1.95，6 V和36 V.在长期贮存条件下，通过定期检测(检测间隔为6个月)，得到10套导弹上述5个关键部件在不同时刻的电压特征值，从2000年到2010年共20个数据.其中1#套导弹的各特征电压值如表1所示.

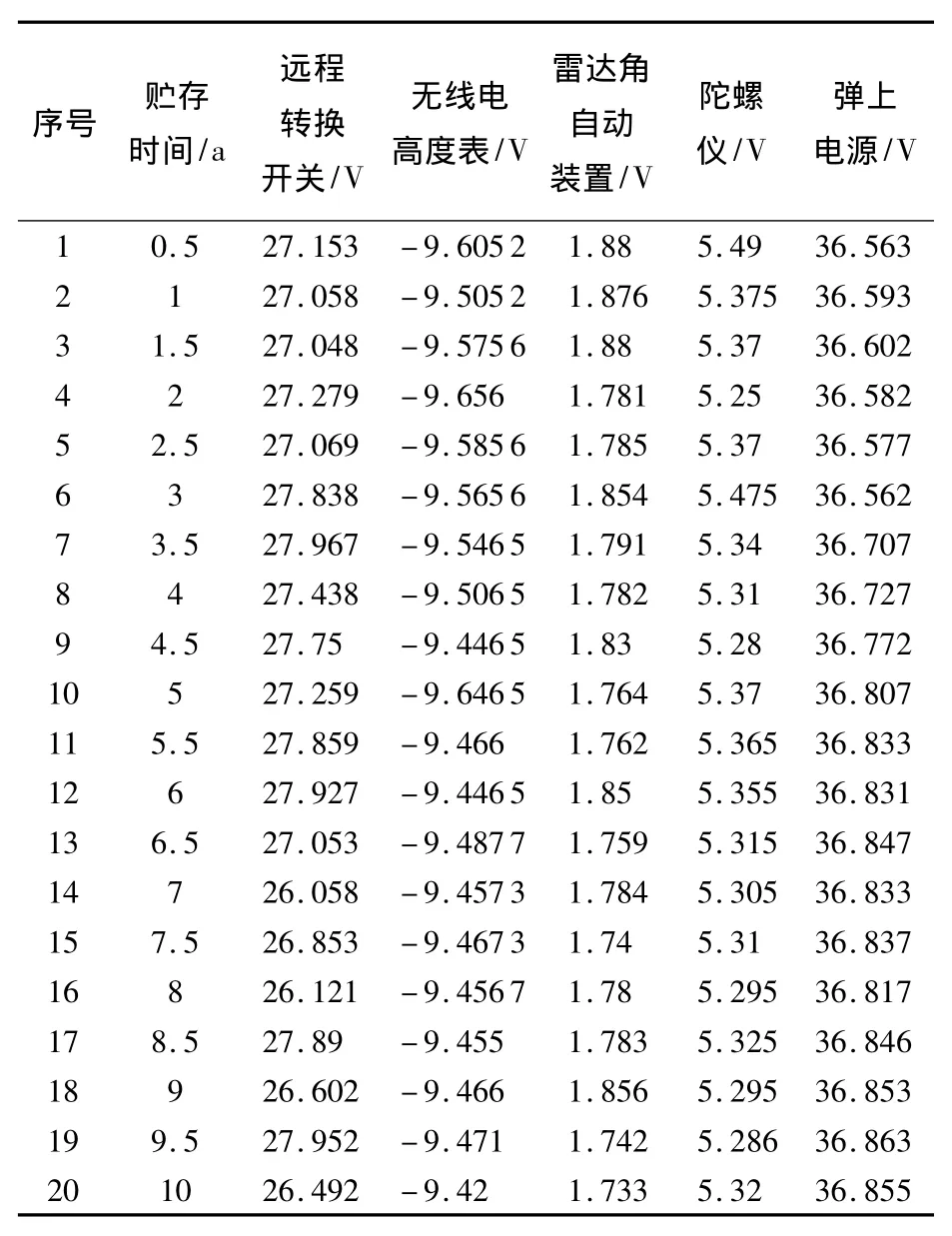
表1 1#套导弹各关键部件特征电压值

2 导弹贮存试验数据随机性分析

将表1中数据进行曲线绘图，得到特征电压值定期检测数据实际变化轨迹，如图2所示.

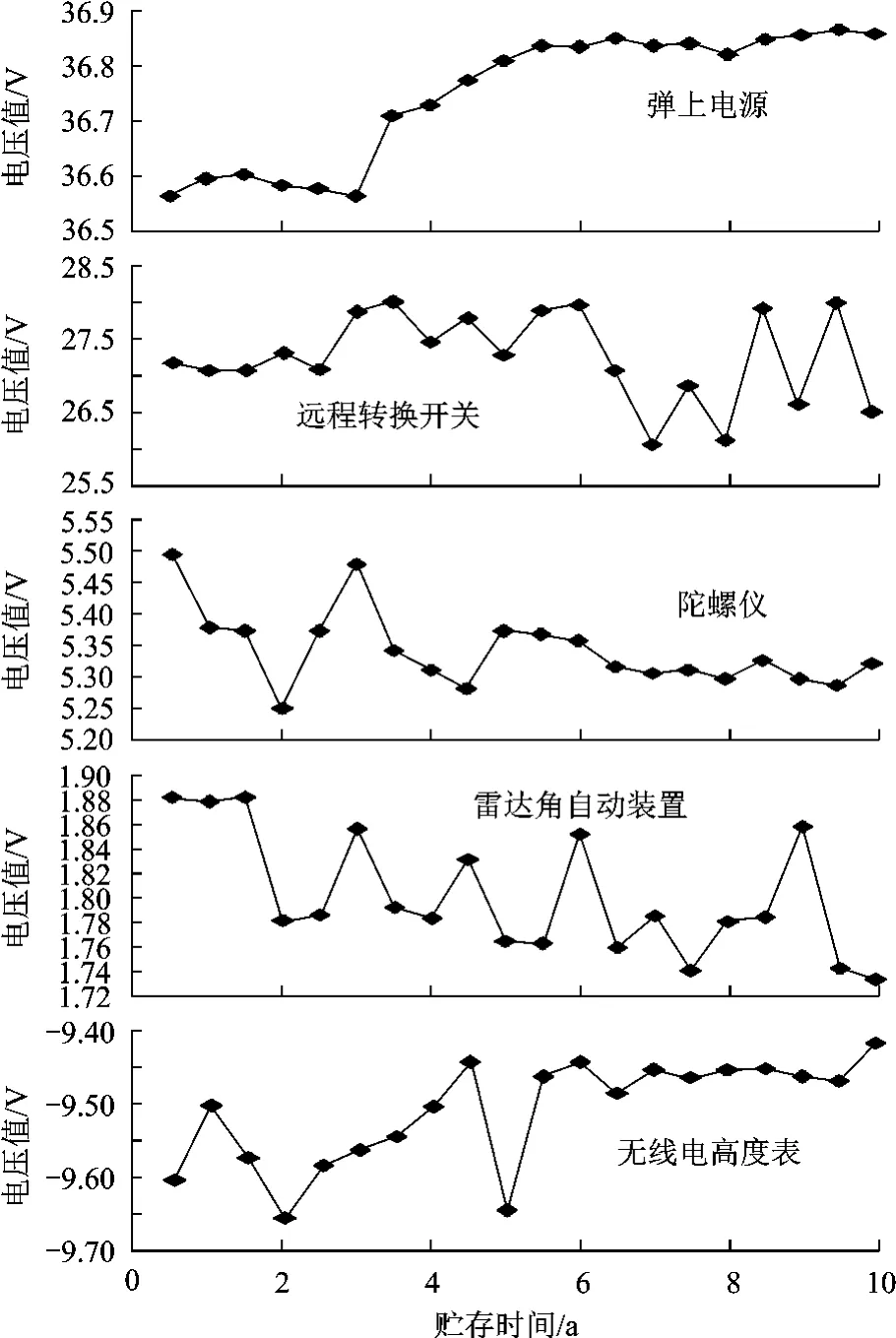
图2 导弹关键部件定期检测数据变化轨迹曲线

从图2中可以看出，在长期贮存条件下，各关键部件特征电压值检测数据随时间没有明显的变化趋势，表现出随机性的变化特点.本文结合信号处理方法中的移动标准差［9］、偏差距离公式［10］等原理，先采用移动标准偏差来分析各关键部件定期检测数据的随机性，即将各时刻特征电压检测值与设计标准值做差后，再采用移动标准差法分析各个阶段随机性波动特点，移动标准偏差计算公式如下:

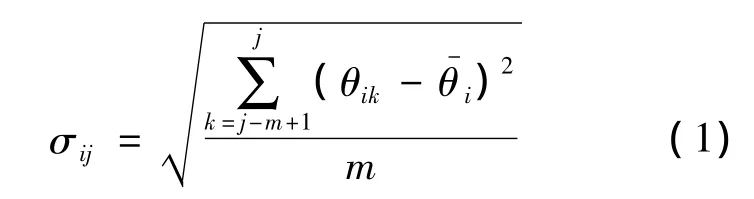
其中，σij表示第i个关键部件在第j时刻的移动标准偏差值;m表示移动步长，取为5，i=1～5依次为表1中所示的远程转换开关、无线电高度表、雷达角自动装置、陀螺仪和弹上电源，j=5～20为表1中第1列所示序号;θik表示第i个关键器件不同贮存时刻的特征电压检测值;θ-i表示各关键器件的特征电压值设计标准值.

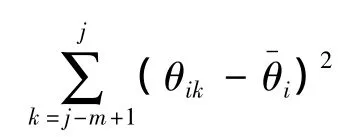
表2 1#套导弹关键部件贮存稳定性水平

在考虑导弹贮存检测数据随机性的基础上，再对表2中的各关键器件特征电压值的贮存稳定性水平进行曲线拟合，分别得到远程转换开关、无线电高度表、雷达角自动装置、陀螺仪和弹上电源贮存稳定性水平随时间的变化规律模型.

远程转换开关变化模型:

式(2)～式(6)中，y1～y5分别表示各关键器件贮存稳定性水平;r表示模型拟合相关系数.

根据长期的历史数据统计结果，工程上一般要求各关键器件贮存稳定性水平阈值依次为:3，1，0.2，2.5 和3.6，可得 1#套导弹远程转换开关、无线电高度表、雷达角自动装置、陀螺仪和弹上电源的贮存寿命依次为:10.77，9.27，18.6，11.43和9.18 a.

3 导弹贮存寿命分散性分析

根据上述导弹贮存试验数据随机性分析思路，依次可得另外9套导弹产品关键器件贮存寿命值，汇总如表3所示.

表3 10套导弹关键器件贮存寿命值

从表3中可以看出，同一关键器件的贮存寿命值在不同导弹中差异很大，主要原因是导弹在材料加工、生产工艺等制造过程中带来的分散性，以及测试仪器和测试过程的分散性等，各类分散性原因的综合结果体现为不同导弹关键器件贮存寿命之间的分散性，可以采用分布检验来描述这种分散性程度.

分别对表3中不同关键器件贮存寿命在10套导弹之间的分散性进行分布假设检验，得到其服从的寿命分布类型和分布参数估计值，且根据不同分布类型与可靠度计算公式之间的折算关系，可得长期贮存条件下考虑分散性的导弹各关键部件的贮存可靠度计算公式，如表4中所示.

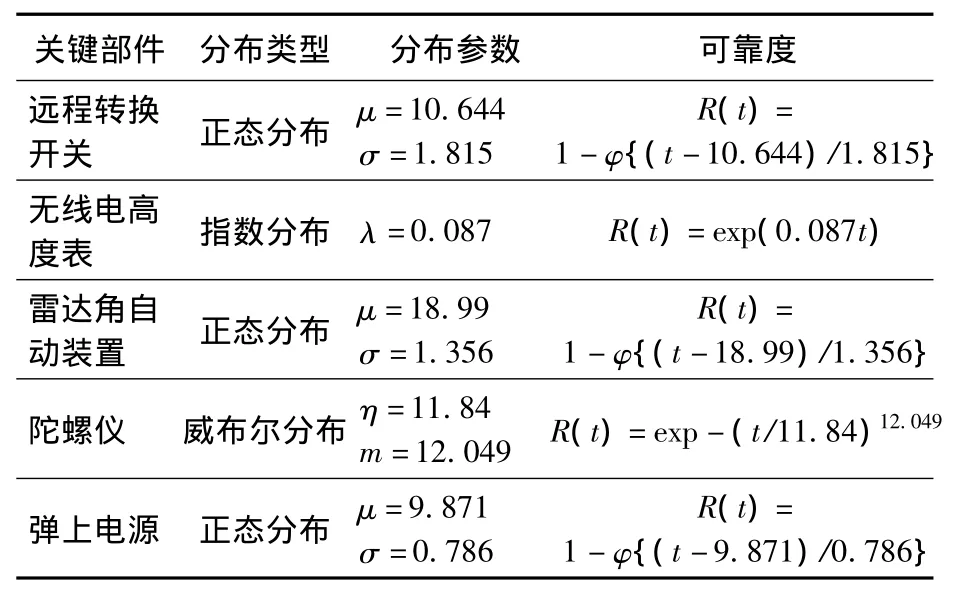
表4 导弹贮存试验数据分散性分析

4 导弹贮存可靠性分析

假设导弹各机理之间相互独立，且在长期贮存条件下各机理随时间发生变化，从而导弹产品的贮存可靠性水平是在机理独立变化条件下，不同退化模式间相互竞争的结果，即在贮存可靠性的分析评价过程中，产品的可靠性水平是由最易退化关键部件的可靠度决定的［11］.根据多机理竞争退化特点，得到导弹贮存寿命的不同考虑情况和在不同寿命考虑情况下导弹可靠性的多机理竞争特点.

根据表4中导弹各关键部件贮存可靠度模型分析结果，通过matlab仿真长期贮存条件下各关键部件可靠度变化规律，得到基于多机理竞争退化的导弹贮存可靠性分析结果如图3所示.

图3 多机理竞争退化下导弹贮存可靠度

结合表3和图3可知，在考虑多机理独立退化的条件下，导弹的贮存可靠度退化规律是一个复杂的过程，具体表现如下:

1)在最悲观期望值下，导弹贮存寿命是由随机性和分散性综合影响下，所有关键部件中的最小寿命值决定的，结合表3中数据有即导弹贮存寿命主要是由3#导弹的无线电高度表的贮存寿命决定，根据图3可得在8.67 a内导弹可靠度也主要由无线电高度表的可靠度决定，且可靠度呈现指数分布退化规律.

2)在最乐观期望值下，导弹贮存寿命是由随机性和分散性综合影响下，所有最大寿命值部件中的最小值决定的，结合表3中数据有即导弹贮存寿命主要是由10#导弹的弹上电源的贮存寿命决定，根据图3可得在11.28a内导弹可靠度分两阶段考虑，在0～10内由无线电高度表的可靠度决定，呈现指数分布退化规律，在10～11.28 a内由弹上电源的可靠度决定，呈现正态分布退化规律.

3)在其他期望值下，导弹贮存寿命处于最悲观期望值和最乐观期望值之间，即为8.67～11.28 a，根据图3可得在这段时间内导弹的贮存可靠度均小0.5，需要进行维护标定方案.

5 结论

对长期贮存条件下10套导弹产品各关键部件的特征电压值进行随机性和分散性分析，通过仿真分析得到了导弹贮存寿命和贮存可靠度之间的权衡关系，本文的主要创新如下:

1)采用移动标准偏差方法分析了导弹各关键部件稳定性水平的变化规律，解决了长期贮存条件下，导弹各特征电压值随机性变化特征难分析的缺陷.

2)采用分布假设检验方法求得导弹各关键部件贮存寿命的分布规律，并据此计算了可靠度模型，解决了各关键器件贮存寿命在分散性影响下难评估的问题.

3)给了随机性和分散性影响下，导弹贮存寿命在不同情况下可靠性分析结果，并对不同期望水平下的导弹贮存寿命和可靠度之间的权衡进行了分析.

本文思路和结论对分析具有随机性、分散性、多竞争退化特点的导弹贮存寿命分析具有重要意义.

References)

［1］ Marotta S A，Kudiya A，Ooi T K，et al.Predicting reliability of tactical missiles using health monitoring data and probabilistic engineering analyses［C］//Proceedings of the 1 International Forum on Integrated System Health Engineering and Management in Aerospace.United States:Society for Experimental Mechanics Inc，2005:7-10

［2］ Chen Haijian，Li bo，Gu Junyuan.Research on missile storage reliability forecasting based on neural network［C］//2012 Sixth InternationaalConference on NaturalComputation (ICNC 2010).United States:IEEE Computer Society，2010:549-553

［3］ AD-A158843.Impact of non-operating periods on equipment reliability［R］.F30602-83-C-0056，1977

［4］王春晖，李忠东，张生鹏.航空导弹贮存期寿命分析［J］.装备环境工程，2011，8(4):68-72 Wang Chunhui，Li Zhongdong，Zhang Shengpeng.Storage life analysis of aircraft missile［J］.Equipment Environment Engineering，2011，8(4):68-72(in Chinese)

［5］高晓敏，吴奎宪，古忠云.导弹及弹药贮存寿命预估方法研究概述［J］.中国材料科技与设备，2009(1):14-19 Gao Xiaomin，Wu Kuixian，Gu Zhongyun.Summary of prediction methods applied to storage life of missiles and ammunitions［J］.Chinese Matertial Science Technology ＆ Equipment，2009(1):14-19(in Chinese)

［6］孙亮，徐廷学，代莹.基于定期检测的导弹贮存可靠性预测模型［J］.战术导弹技术，2004(4):16-19 Sun Liang，Xu Tingxue，Dai Ying.Models of storage reliability prediction based on periodical test for missiles［J］.Tactical Missile Technology，2004(4):16-19(in Chinese)

［7］吴进煌，戴邵武，徐胜红.基于可靠度预测模型的导弹贮存寿命分析方法［J］.2005，20(4):477-479 Wu Jinhuang，Dai Shaowu，Xu Shenghong.Analysis method of missile storage life based on forecasting model of storage reliability［J］.Journal of Naval Aeronautical Engineering Institute，2005，20(4):477-479(in Chinese)

［8］胡东，谢劲松，吕为民.PHM技术在导弹武器系统中的应用前景探讨［J］.导弹与航天运载技术，2010(4):24-30 Hu Dong，Xie Jinsong，Lü Weimin.The application prospect of PHM in missile weapon sysem［J］.Missiles and Space Vehicles，2010(4):24-30(in Chinese)

［9］ Pavlenko Y F，Ogar V I，Kolbasin A I，et al.A mobile standard of frequency deviation unit in frequency modulation signals［C］//Precision Electromagnetic Measurements.Digest，1996 Conferece on.Braunschweig:IEEE.1996:285-286

［10］ Shibuya N，Umeda K.Self-localization of a mobile robot using compressed image data of average and standard deviation［C］//The 18thInternational Conference on Pattern Recognition(ICPR’06).United States:Institute of Electrical and Electronics Engineers Ins，2006，4:614-617

［11］吕萌，蔡金燕，张志斌.多退化模式下的电子装备可靠性建模［J］.火力与指挥控制，2009，34(10):164-170 Lü Meng，Cai Jinyan，Zhang Zhibin.Electronic equipments reliability modeling research under multi-degradation mode［J］.Fire Control＆ Command Control，2009，34(10):164-170(in Chinese)