基于遗传算法的层合板分级铺层全局优化
2013-11-05刘振国
刘振国 胡 杰 胡 龙
(北京航空航天大学 航空科学与工程学院,北京100191)
由于复合材料的比强度、比刚度较高,近年来应用十分广泛.通过改变铺层形式和厚度来改变刚度、强度、屈曲和振动等性能是复合材料设计的一个优势.遗传算法作为一种高效的离散空间搜索算法,在复合材料铺层的优化设计中适用性较好,国内外学者对其进行的研究较多[1].文献[2-5]对层合板的遗传算法本身的改进作了研究,提高了收敛率,避免了早熟现象的产生.文献[6]使用了神经网络和遗传算法分别对层合板的铺层比例和铺层顺序进行了优化,但其将两者的优化看成是两个独立的过程,并不能达到最优化的结果.另外该方法不对整体铺层数量进行优化.上述研究中在模拟结构力学性能方面均采用了经典层合板理论,优点是较为可靠、计算量较小,但是难以处理结构形状复杂和边界条件复杂的问题.目前在处理实际优化问题上,有限元方法逐渐成为主流.文献[7]借用有限元分析结合特殊设计的遗传算子,实现了铺层材料、铺层顺序和铺层厚度的优化.文献[8]提出了一种改进的遗传算法用以实现复合材料的多学科优化.文献[9]引入了层合板弯曲刚度等中间参数,降低了优化过程的有限元计算量.但他们的研究仅限于对层合板的整体优化.
由于在诸如飞机机翼翼面、螺旋桨叶片等大面积应用复合材料的部件上受力复杂,应力变化比较剧烈,采用相同的铺层会降低材料的效率,而独立分区优化未考虑相互间的联系,难以达到整体目标函数的最优解,所以有必要研究在分区设计的基础上进行整体的优化.目前有关分区设计方面的研究成果较少.分区设计的缺点一方面是设计变量大大增加,另一方面区域与区域间差异较大的铺层过渡也会对工艺性提出挑战.文献[10]提出了一种复合材料全局优化方法,通过对已经分区的层合板进行补强的方式,对复合材料快艇艇身进行了优化,得到了工艺性较好的结果.文献[11]通过多岛遗传和序列二次规划法相结合的形式对机翼翼盒段进行了整体优化,翼盒间相互独立,其内部保持铺层一致,未考虑工艺.
本文结合整体和分区域设计的优势,提出了公共铺层和局部铺层共存的分级优化模式,一方面保存了对局部区域特殊承载进行特殊设计的能力,另一方面全局铺层的存在也保证了更好的工艺性,减少了设计参数可节约计算时间.另外,通过变异操作实现了铺层的增减也降低了铺层厚度变更的复杂程度.通过Python语言进行遗传算法的流程的实现,驱动ABAQUS进行模型的分析计算,实现层合板分级遗传、铺层顺序和铺层厚度的优化.
1 单元模型
通过ABAQUS的用户自定义子程序,将经典层合板理论计算的刚度矩阵和失效形式植入单元计算.使得优化过程仅需输出铺层形式即可进行力学分析和失效判定.失效判定过程对每个单层逐一进行校核,单层失效即判定为失效.
1.1 刚度矩阵计算
由经典层合板理论[12]得层合板合成轴力和弯矩为

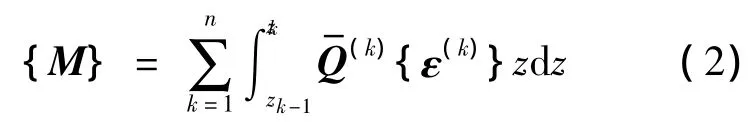
其中,ε(k)为第 k层层合板产生的应变,ε(k)={εx(k),εy(k),εz(k)};Q-(k)为第k层层合板的刚度矩阵;zk为第k层中心沿厚度方向坐标.
由此,对于给定铺层顺序、厚度及铺层角的层合板,即可求得层合板刚度.
1.2 破坏判定准则
判定层合板破坏存在多种准则,本文取平面应力状态Tsai-Wu张量准则作为破坏判定条件[2]:

分析时,令式(3)左侧计算值为强度因子STW,在每个单元内对铺层进行逐层校核,判断是否失效.
2 遗传算法
遗传算法是一种离散的空间搜索算法.通过将可能的解编码成一向量——染色体,通过一代代的复制、交叉、变异操作,选出适应度最好的染色体,即获得最优解.
2.1 基因编码
虽然层合板中铺层顺序不会改变材料的拉压性能,但是会对承弯性能造成影响,所以仍需对铺层进行排序.规定每层厚度T,用一定顺序的数字串表示按此顺序排布的铺层.采用对称形式铺设,仅将一半用基因表示,铺层基因编码从左向右对应铺层从内向外.为保证铺层对称性,±45°铺层成对出现,两层厚度值均设定为T/2.如下所示,其中 1,2,3 分别对应铺层角 0°,±45°和90°,0 表示对应层不铺:
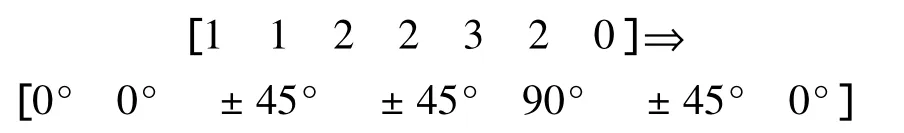
对于给定铺层而言,在何位置插入0,对铺层本身不产生影响,但是破坏了基因-铺层之间的一一对应关系.为防止这种情况的发生,0只存在于队列末尾.如变异或交叉产生编码形式不符合条件,自动传递至末尾,其后铺层向前靠一位.
为实现多区域铺层的全局优化,对于每一个区域提供不同的铺层建立独立的基因编码Nr,从而建立对于全局的公共铺层Nw.计算过程中,全局铺层也按对称形式,铺设于区域层表面,全局铺层基因设置于基因链末尾,该铺层也参与优化过程,以获取最优结果.为了防止区域间厚度变化过大影响工艺性,需要对铺层厚度变化范围给出限定.限定 Nr和 Nw的最大值分别为 Nr,max和 Nw,max,最小值分别为 Nr,min和 Nw,min.如图1所示 3 个区域,Nr,max=6,Nw,max=7 时的铺层示意图.如该基因所表示的铺层1对应的区域1的实际铺层(包含区域与全局铺层,并且为对称排布)应为
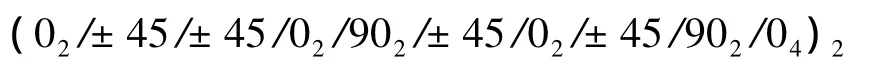
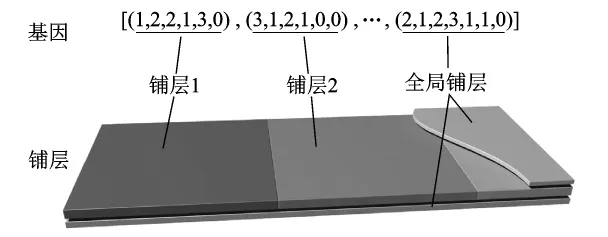
图1 分级铺层方式示意
区域铺层与区域铺层之间如果对应层铺角不同,则采用错位搭接方式,厚度变化不连续则采用逐层递减方式过渡.由于过度区域强度增加,为降低分析复杂程度,减少计算时间,本文不再单独对该区域进行力学分析.另外,过渡区域在质量上的增加可忽略不计.
2.2 遗传算子
选择与交叉:选择过程采用蒙特卡罗方法,每个个体的选择概率和其评估值成正比.
交叉:以一定交叉率pc进行交叉.为提高个体之间的交叉频率,遵循多点交叉原则.父本与母本的对应区域基因相互交叉产生子代个体,不同区域之间不交叉.交点和选取的基因段均随机确定.如图2例举了父代一种可能的交叉生成子代方式.

图2 交叉过程
变异:以一定变异概率pm随机抽取一个个体,选择其中一个基因进行突变.根据给定的变异率进行变异操作,变异区域有相同概率增加或者减少一层.增加铺层时,随机选取其中一层,置于之前,铺层角度随机产生.若该区域铺层数已达最大值,则删去最后一层.减少铺层时,随机选取其中一层将该层删去,若该区域铺层数已减至最小值,则不再进行删去操作.图3显示了当区域变异后层数超过限定层数时的操作过程.

图3 变异过程
2.3 精英算法改型[13]
为了保存每代最优的个体,使用的是保护精英的方法.交叉变异操作生成的子代与亲代混合排名,取前Nelite个作为精英,直接传递到下一代,剩下的名额由之前产生的子代排名靠前的补满.第一代个体基因随机产生,第二代开始采用精英保护保存优良个体.
3 评估函数设计
3.1 适应度函数
对应多目标优化,适应度函数取权重函数,其形式为
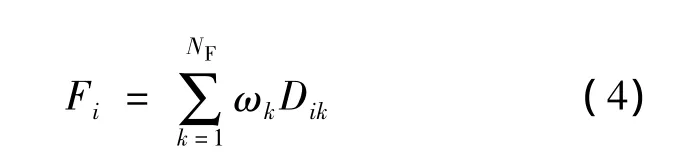
其中,Dik为对应第i个个体的第k个权重参数的无量纲值;ωk为该参数的权重系数,总和为1;NF为适应度函数权重参数个数.权重参数取设计过程中主要关注的变量,如结构形变、重量、整体刚度(应变能)等.Dik=dik/Sk,Sk根据初始设计对应计算结果给出.若无初始设计方案,则按给定最大层数下π/4板(0/±45/90)2计算.
3.2 适应度函数改进
对于计算过程中需要获取最小适应度值的个体,需要对适应度作适当调整.另外,使用统一的适应度算式存在算法前期适应度很高的个体优势特别突出的问题,以致产生超级个体,造成早熟的缺陷,并且在后期个体适应度差异缩小时也会降低遗传效率.综合考虑以上两方面,对适应度值作以下调整:

其中,b为Fi理想最小值;a为Fi平均值与最小值之差,保证平均值的适应度为0.5时Fi与b的距离.取β=2,为了起到调节作用,对α早期取0.5,中期取1,后期取2.
由于计算过程中,每一个算例的理想值较难估算,过大过小都会延缓遗传进化速率,为此,本文取b为群体本代的最小值,使得每一代均能且仅能产生一个适应度为1的个体.这么做的缺点是使得每一代调整后的适应度值F*i与本代最大适应度值Fi,max相关,不能逐代比较F*i.另外,采用精英算法时,考虑了父子两代的适应度,所以,将b修正为父子两代群体F*i最小值.
3.3 惩罚函数
对于实际遗传计算过程中,不满足约束条件的个体,如果直接对其抛弃,会对种群的多样性产生影响,这种情况在最优解在边界附近时尤为明显.为此,采用惩罚不可行解的方法将约束问题转化为无约束问题.对于给出的约束条件,选取乘法形式的评估函数
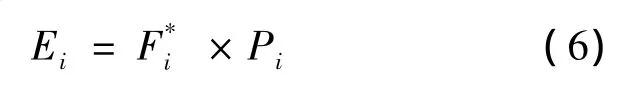
其中Pi为罚函数.采用文献[14]提出的惩罚函数,对于约束gk≤bk,计算式如下:
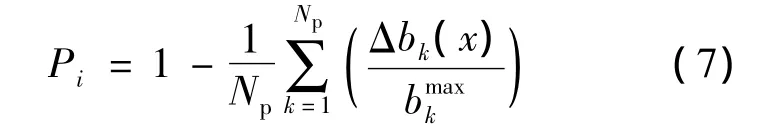
其中,Δbk=max{0,gk-bk};Δbmaxk=max{ε,Δbk},为避免分母为0给出的小正数;Np为给出的约束条件总数.同样需要注意,采用精英算法时,将bmaxk修正为父子两代的违反量最大值.
3.4 其他计算考虑
随着遗传过程的进行,产生相同基因个体的概率越来越大.由于采用ABAQUS计算一个实例的时间较长,重复计算将对资源造成极大的浪费.为防止此类状况的发生,对历代每个已计算的个体基因和计算结果进行保存,每次进行模型计算前,对待解基因与已存基因进行逐个比对,若已进行过计算,则将计算过程跳过,直接输出之前的结果,否则进行计算.为方便比较,将基因序列看成4进制数值,转化成10进制值Ngen保存,如铺层为[1,1,2,2,3,2,0]时,Ngen=5 816.若将整个基因链整体转化保存,Ngen会随着区域数量增加呈几何倍数上升,不利于比较,因此需进行逐区域保存,逐一比较两个个体对应区域的Ngen,若相同则判定为同一个个体.
4 算例
参照文献[15]算例1并根据对称原则截取一半,设计算例如下:一块长宽为40 mm×15 mm的层合板,受力形式如图4所示,两长边自由,一短边AB限制x向位移和绕y轴旋转,并受不同方向均布线载 f1和 f2,取 f1=20 N/mm,f2=50 N/mm.考虑到剪力在平板内基本不变,板受弯沿x方向逐渐变化,将其沿x方向分为3个区域进行优化.

图4 模型受力及分区示意图(单位:mm)
设定单层铺层厚度T=0.2 mm,ρ=1.56 g/mm3,设定适应度权重参数为结构重量和层合板A,B点间平均位移.对等厚度(6.4 mm)π/4板计算后,取去量纲因子 S1=5×10-6kg,S2=0.5 mm,取ω1=0.5,ω2=0.5.约束为各区域每个单元每个单层Tsai-Wu准则下不失效,安全因子取1.遗传算法方面,设定最高遗传100代,每代种群个数为100.由于使用了精英算法保证了最优结果遗传的完整性,所以取稍大的交叉率和遗传率:pc=0.9,pm=0.05.另外,铺层方面取 Nr,max=7,Nw,max=9,Nr,min=3,Nw,min=4.
分级铺层优化遗传过程见图5.层合板最优结果在第 41 代出现,最优铺层为[(2,2,2,1,1,1,1),(2,2,2,2,1,1,0),(2,2,2,0,0,0,0),(1,1,1,1,1,1,1,1,0)],对应质量 m=4.786 579 ×10-3kg,位移,w=0.190 642 3 mm,最优适应度 F=0.6693002,STW,max=0.2123366.

图5 层合板优化计算结果
总体上,由于剪切刚度对铺层厚度不敏感,而外层的承弯效率更高,因此优化结果中内层由±45°铺层占据,外层均为0°,符合实际情况.剪切力沿板x方向基本不变,所以±45°层厚度基本相同.而区域1由于要承担更大的弯曲应力,所以较区域2的0°铺层所占的比例更大,区域3所承担的弯曲应力最小,由于有全局铺层的存在,所以不再出现0°铺层,而层数减小至3层.由于算例中不存在沿y方向的外力,所以优化结果中不含有90°铺层.
为证明该铺层形式为设计条件下的最优解,现通过有条件的穷举法证明.由上述分析可知,区域最优形式铺层分布为内层为±45°,外层为0°,0°在区域1中所占的比例最大,在区域3最小.另外,全局铺层在区域铺层最外层均为0°的情况下,均为0°.对穷举满足条件的105717种情况进行计算统计,证明该铺层方案是最优解.
若采用不分级仅分区优化方式,由于将所有整体铺层都拆分成了区域铺层,相较于分级铺层方式,增加了设计变量,因此在计算时间上增加了37%.计算结果是最优铺层在区域1中增加了1层0°铺层,其他区域中与分级铺层方式优化结果相同,适应度值减少1%,差别较小,因此付出的计算效比不高.
对于同一个算例,其他参数保持不变,仅取ω1在0.1~0.9之间变化,得到分区优化结果如表1所示.由表1可见,随着质量权重的增加,各区域和全局铺层数量逐渐减少,直至ω1=0.9时全体减至最低铺层数.ω1=0.7时区域2铺层的增加是建立在全局铺层减少2层的基础之上的,综合而言,该区域铺层总数是减小的.另外,铺层中0°铺角比例逐渐增加,以便在有限质量内保证一定的弯曲刚度.所列最优铺层结果均未破坏,STW,max=0.3851623,出现在 ω1=0.9 处.
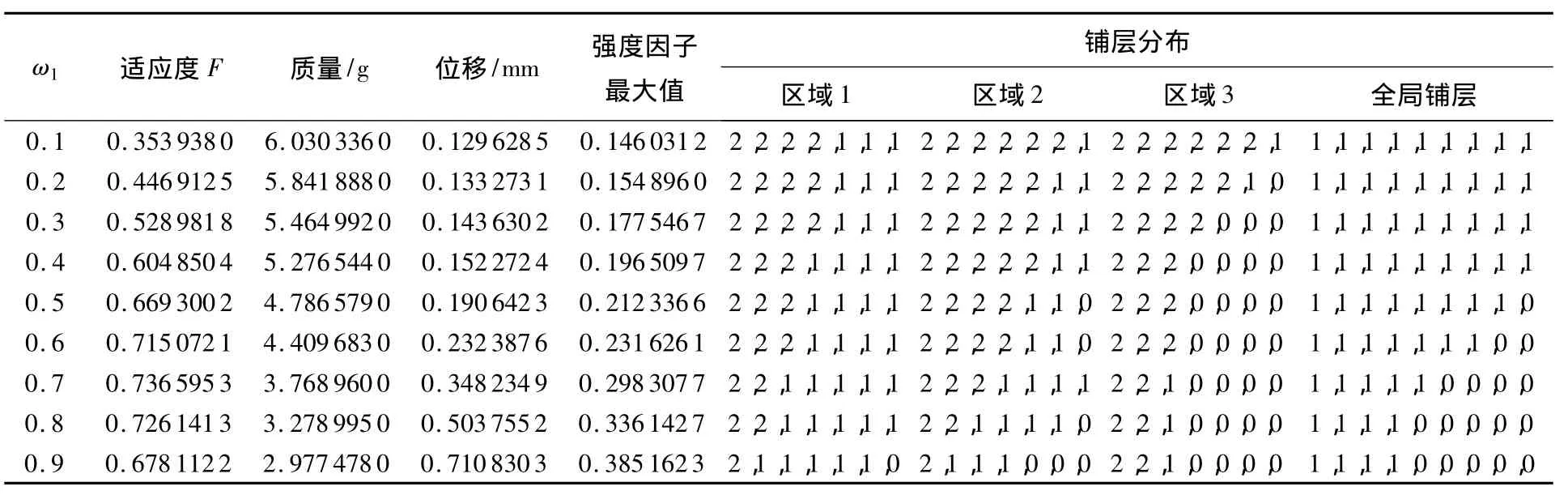
表1 分级铺层优化结果随质量权重因素ω1变化
本文也对不分区的整体优化方式进行了计算(即令区域数为1).为保证设计空间的一致性,设最大铺层数为上例 Nr,max与 Nw,max之和,最小铺层数为 Nr,min与 Nw,min之和,其他条件不变.图6表示了分级优化比整体优化最优适应度增加的百分比随ω1的变化趋势.整体上随着质量权重系数的增加(ω1值增加),两者差距逐渐增大.由此可见,对质量要求越苛刻,则分级设计的优势越明显.ω1=0.9处时百分比产生较大下降的原因是本文设置的最低层数影响了质量的进一步降低、区域间差异扩大的实现,事实上,在ω1=0.4处时,最低层数的限制已经开始影响到了区域3的铺层改变.

图6 整体比分级优化最优适应度增量百分比随ω1的变化
5 结论
本文建立了层合板刚度模型,实现了对层合板铺层角和厚度的遗传优化.一方面,通过对分区铺层进行单独优化和提出整体结构目标函数,考虑各个局部应力,能够比整体铺层优化得到受力形式更加细致合理的铺层分布.另一方面,由于一般情况下应力在结构上是连续分布的,全局铺层的存在,体现了针对整体应力分布的铺层设计,保护了该部分铺层的完整性,也在一定程度上节约了计算资源.本文算例表明,分级铺层遗传优化过程收敛较快,优化结果合理可信,在应力分布较为复杂的层合板中更能发挥优势,更能达到降低结构质量、提高结构刚度等目的.另外本文优化分析过程结合了有限元计算方法,使得即使应用复杂形状的层板模型,其分析也变得简单易行.
本文的计算过程中,区域是人为划分的,全局铺层、区域铺层的最大层数和最小层数均是人为给定的,并没有进行定量的规划,影响了最优结果性能的进一步提高.因此如何根据初步设计的应力分布选择区域数量、进行自动区域划分,如何根据应力变化幅度设定铺层变化范围,将成为进一步提高优化能力的研究方向.
References)
[1] Akbulut M,Sonmez F O.Design optimization of laminated composites using a new variant of simulated annealing[J].Computers and Structures,2011,89(17/18):1712-1724
[2]晏飞,李为吉.基于自适应遗传算法的复合材料层合板铺层顺序优化方法[J].西北工业大学学报,2001,19(1):156-159 Yan Fei,Li Weiji.A stacking sequence optimization method of composite laminated panel based on an adaptive genetic algorithm[J].Journal of Northwestern Polytechnical University,2001,19(1):156-159(in Chinese)
[3]杨建国,李蓓智,俞蕾.基于免疫遗传算法的优化设计[J].机械设计,2002,19(9)14-17 Yang Jianguo,Li Beizhi,Yu Lei.Optimization design based on genetic algorithm of Immunity[J].Journal of Machine Design,2002,19(9):14-17(in Chinese)
[4]鲁大伟,李书.应用免疫遗传算法优化设计层合板铺层顺序[J].北京航空航天大学学报,2005,31(2):247-250 Lu Dawei,Li Shu.Stacking secuence optimization of composite laminate applying genetic algorithm of immunity[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(2):247-250(in Chinese)
[5]任茶仙,张铎.复合材料层合结构铺层顺序优化设计的免疫遗传算法[J].强度与环境,2007,34(2):43-50 Ren Chaxian,Zhang Duo.Immunity genetic algorithm for stacking sequence optimization in composite laminated structures[J].Structure & Environment Engineering,2007,34(2):43-50(in Chinese)
[6]修英姝,崔德刚.复合材料层合板稳定性的铺层优化设计[J].工程力学,2005,22(6):212-216 Xiu Yingshu,Cui Degang.Plyoptimization design for stability of composite laminates[J].Engineering Mechanics,2005,22(6):212-216(in Chinese)
[7] Almeida F S,Awruch A M.Design optimization of composite laminated structures using genetic algorithms and finite element analysis[J].Composite Structures,2009(88):443-454
[8] Park C H,Lee W I,Han W S.Improved genetic algorithm for multidisciplinary optimization of composite laminates[J].Comput Struct 2008,86(19/20):1894-1903
[9]乔巍,姚卫星.复合材料加筋板铺层优化设计的等效弯曲刚度法[J].计算力学学报,2011,28(2):158-162 Qiao Wei,Yao Weixing.Equivalent bending stiffness method for stacking sequence optimization of composite stiffened panel[J].Chinese Journal of Computational Mechanics 2011,28(2):158-162(in Chinese)
[10] Zehnder N,Ermanni P.A methodology for the global optimization of laminated composite structures[J].Composite Structures,2006(72):311-320
[11]唐振杰,李玉龙.基于等效刚度矩阵的复合材料机翼盒段优化设计[J].南京航空航天大学学报,2011,43(4):521-525 Tang Zhenjie,Li Yulong.Optimization design for box of composite wing based on effective stiffness matrix[J].Journal of Nanjing University of Aeronautics and Astronautics,2011,43(4):521-525(in Chinese)
[12]王耀先,复合材料结构设计[M].北京:化学工业出版社,2001:83-87,34 Wang Yaoxian.Composite structure design[M].Beijing:Chemical Industry Press,2001:83-87,34(in Chinese)
[13] Almeida F S,Awruch A M.Design optimization of composite laminated structures using genetic algorithms and finite element analysis[J].Composite Structures,2009(88):443-454
[14] Gen M,Cheng R.Optimal design of system reliability using intervel programming and genetic algorithms[J].Computers Ind Engng,1996,31(1/2):1-29
[15] Huang Zhengming,Inelastic and failure analysis of laminate structures by ABAQUS incorporated with a general constitutive relationship [J].Journal of Reinforced Plastics and Composites,2007,26(11):1135-1181
