多项式基函数神经网络的结构可靠性分析

孟广伟 李广博 李 锋 周立明

(吉林大学机械科学与工程学院，长春130025)

1 问题提出

根据工程结构可靠度的定义[1]，结构的功能函数可以表示为

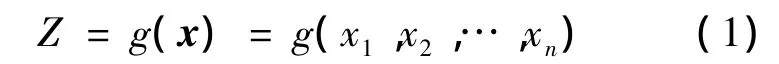
其中x=(x1，x2，…，xn)，表示结构的基本随机变量，例如材料属性、载荷、几何形状等.规定Z＞0表示结构处于可靠状态，Z＜0表示结构处于失效状态，Z=0表示结构处于极限状态.结构不能完成预定功能的概率，即失效概率为

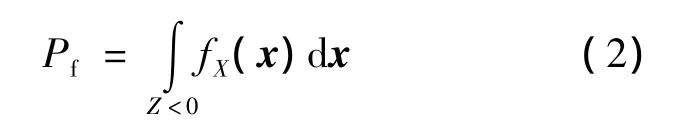
其中fX(x)=fX(x1，x2，…，xn)是x的联合概率密度函数.

近年来，很多方法用于计算上述失效概率Pf，例如蒙特卡洛模拟法(MCS，Monte Carlo Simulation)，一阶可靠性方法(FORM，First-Order Reliability Method)，二阶可靠性方法(SORM，Second-Order Reliability Method)等[2].对于一些功能函数为隐式或者较复杂的结构，以上方法均非常耗时，给计算带来麻烦，甚至在某些情况下还可能会出现不收敛的情况[3].为解决上述问题，一些方法被提出.响应面法(RSM，Response Surface Method)，是其中应用较广泛的[4－6].假定被挑选出来的结构功能函数能够很好的模拟其真实的曲面，计算其失效概率可达到一定精度，但是复杂工程计算中，不能保证响应面能准确逼近其真实的情况，当随机变量的数目庞大时，将耗用大量的计算时间.同时固定的函数形式影响其普遍性[7].人工神经网络法同样被广泛应用于结构可靠性的计算[8－9].传统的反向传播(BP，Back-Propagation)神经网络在计算中易陷入局部最小过程，收敛速度慢.径向基函数神经网络[10]和切比雪夫基函数[11]在一定程度上提高了函数逼近的精度，但是表达形式比较繁琐，不利于编程计算.

本文采用多项式基函数神经网络代替传统响应面函数，基于广义逆矩阵的方法计算网络权值，拟合功能函数的真实极限状态曲面，结合可靠度计算的一阶可靠性方法，计算功能函数的失效概率.本方法提高了解决非线性隐式极限状态方程可靠性问题的能力，提高了收敛速度.数值算例表明此法编程简单，达到了较好的效率和精度要求.

2 多项式基函数神经网络模型

2.1 多项式基函数

基于文献[12]，一个单隐层的神经网络在进行函数逼近时，完全等价于某个高阶的多元多项式函数.图1表示一种多输入多项式基函数隐神经元模型.输入层xt(t=1，2，…，n)与隐含层神经元的连接权值恒为1，隐含层神经元与输出层的连接权值为ωh(h=1，2，…，u).

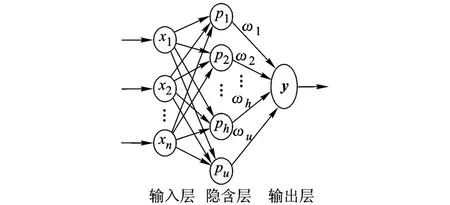
图1 多项式基函数神经网络模型

对于未知非线性目标系统G(x1，x2，…，xn)，设对应的多项式神经网络的输入变量分别为x1，x2，…，xn.隐层神经元的激励函数为一组如式(3)所示的多项式基函数.

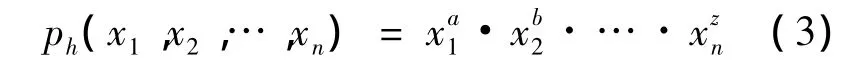
其中a=0，1，2，…，i;b=0，1，2，…，j;z=0，1，2，…，l;i=j=l=0，1，2，….

基于多元多项式逼近理论[13]，设Ω⊂Rn是有界闭集，C(Ω)表示Ω上所有实值连续函数构成的空间.R⊂C(Ω)是一个代数，G(p)∈C(Ω).为使目标函数G用R中元素一致逼近，只须对∀ph∈Ω和∀ε＞0，均能找到一个函数L∈R，使得

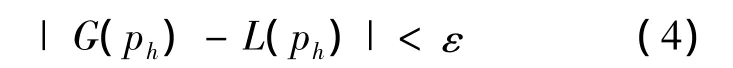
则目标函数G(x1，x2，…，xn)在Ω上能用x1，x2，…，xn的多项式逼近，表示为

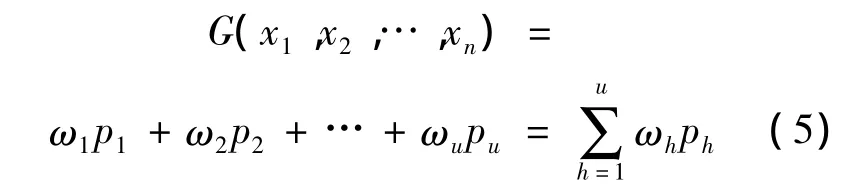
其中，ω1，ω2，…，ωu为网络隐含层与输出层的连接权值，即权系数;p1，p2，…，pu为多项式基函数.

与传统的单隐层前向神经网络相比，该模型最大的优点是仅有隐层至输出层的权值需要确定，极大地改善了网络的结构设计.

2.2 网络权值的确定

传统的基于梯度下降的BP迭代法计算网络隐含层与输出层连接权值的公式为

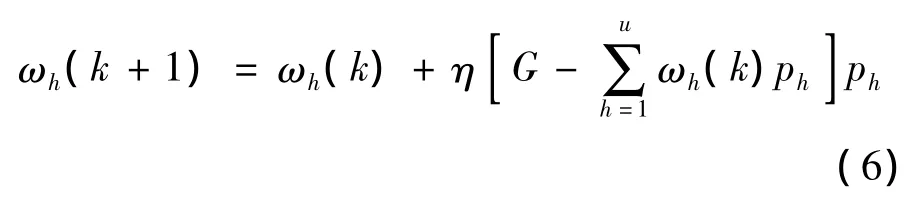
其中，η为迭代步长;k为迭代次数;u为隐神经元数.

在计算式(6)的权值时，需要大量的迭代计算，且容易陷入局部最小的情况.为克服BP学习算法的固有缺陷，采用下面的权值计算方法.

设网络输出为

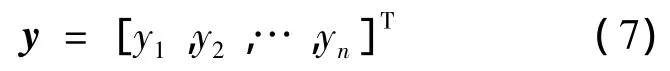
隐含层与输出层的连接权值为

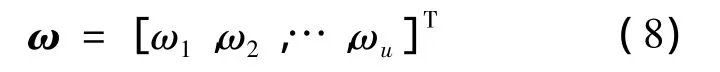
隐层神经元的激励响应矩阵为

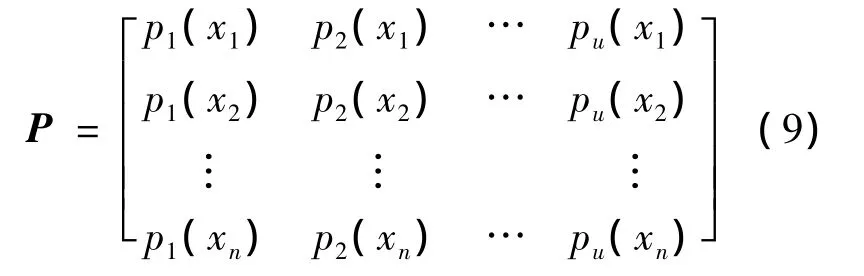
则对于图1的多输入多项式基函数神经网络权值直接确定为其中P+=(PTP)－1PT为激励响应矩阵的广义逆矩阵.

3 多项式基函数神经网络法的结构可靠性分析

3.1 多项式基函数神经网络法

为使达到计算精度的同时保证计算效率，取i=j=l=2，a，b，…，z系数依次由低到高.可设响应面函数为

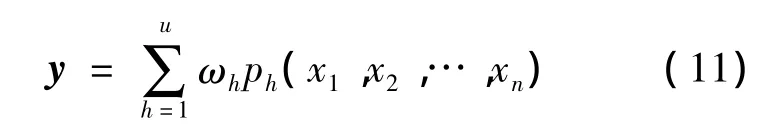
为了保证网络的稳定性和计算精度，对神经网络的输入变量x按如下变化:

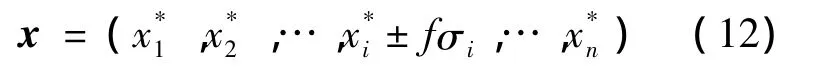
式中，f为任意因子;x*i为随机变量的均值;σi为随机变量的标准差.

相对应网络的函数估计值y即为

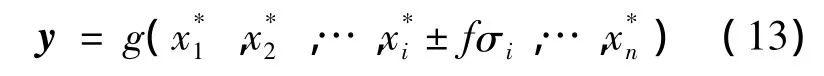
3.2 多项式基函数神经网络法的计算过程

网络在迭代计算验算点时，为使其计算简便，将非正态分布的变量进行标准变换，在标准空间进行迭代计算.

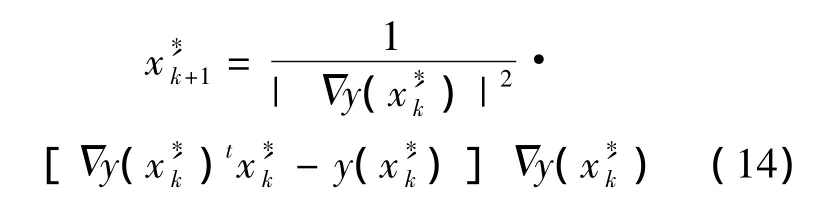
基于二次多项式响应面法的计算原理，多项式基函数神经网络法的可靠性计算流程见图2.

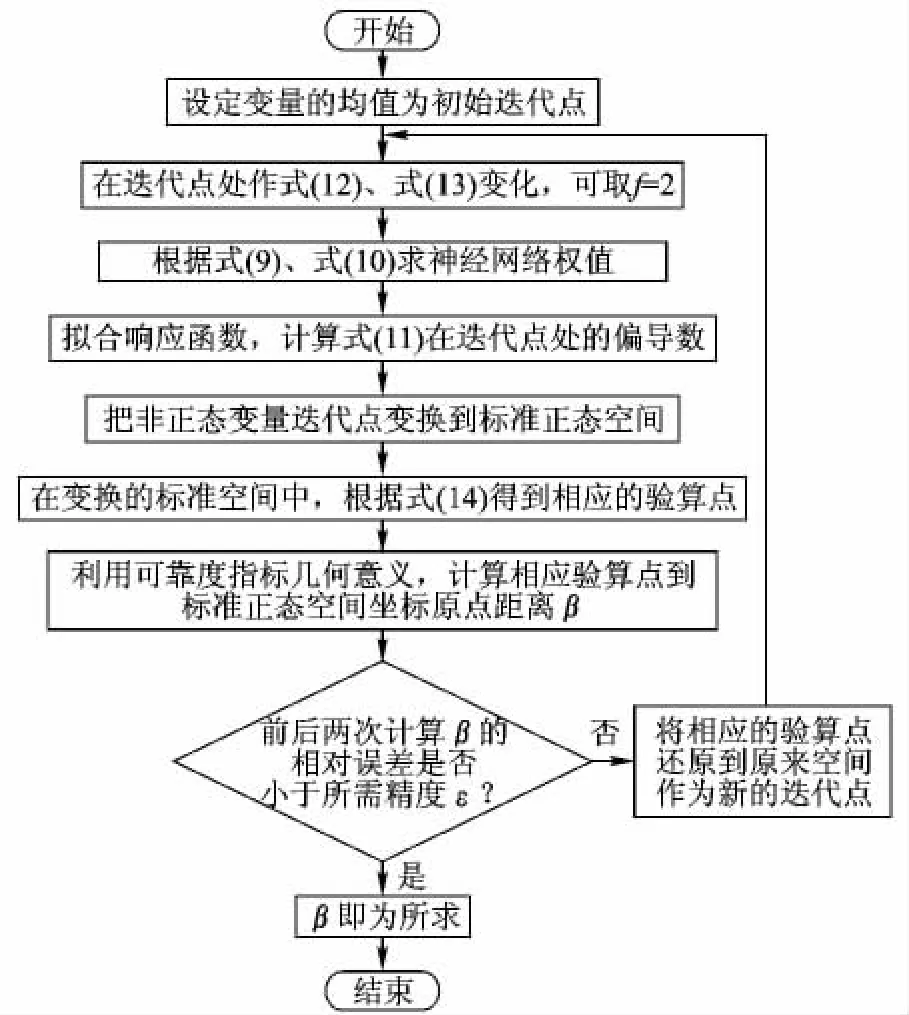
图2 计算流程图

4 数值算例

4.1 算例1

考虑一个非线性功能函数[14]:

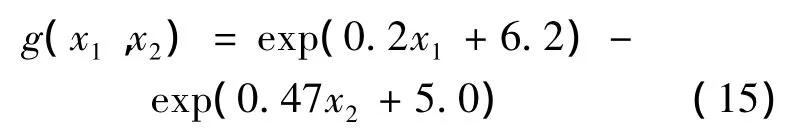
其中x1和x2相互独立且均服从标准正态分布.MCS的计算结果可认为是精确解.通过表1的计算结果比较，表明了本文方法计算非线性程度较高的功能函数时，精度高.

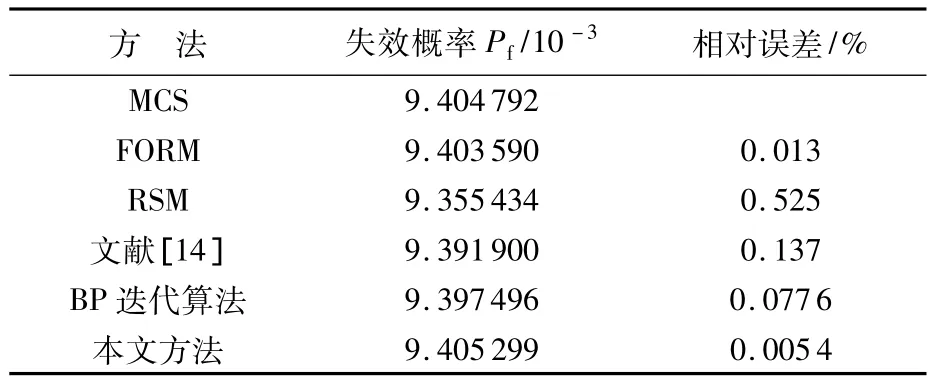
表1 算例1的失效概率计算结果

4.2 算例2

考虑一个非线性功能函数[15]:

其中，x1～N(1000，2002);x2～N(250，37.52).

通过 MCS计算的失效概率 Pf=9.607×10－3.表2列举了其他几种计算方法的结果.通过表2的比较，表明本文的方法在计算精度上有一定优势，失效概率的相对误差仅为0.60%，进一步证明本方法的高效性.

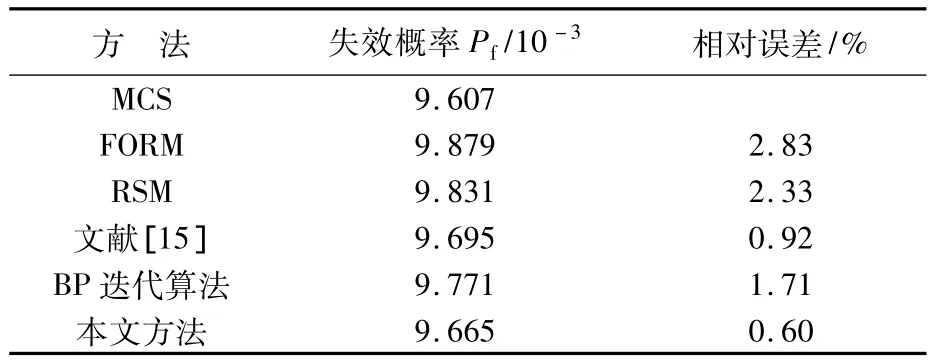
表2 算例2的失效概率计算结果

4.3 算例3

如图3所示的屋架，屋架的上弦杆和其他压杆采用钢筋混凝土杆，下弦杆和其他拉杆采用钢杆.屋架承受均布载荷q作用，将均布载荷q化成节点荷载后有 P =ql/4.设 Ac，Ec，As，Es，l分别为混凝土和钢杆的横截面积、弹性模量、长度.Ec=2×1010MPa，Es=1 × 1011MPa，l=12m.定义 q ，Ac，As为服从正态分布的随机变量，分布参数见表3.

表3 基本随机变量统计特征值

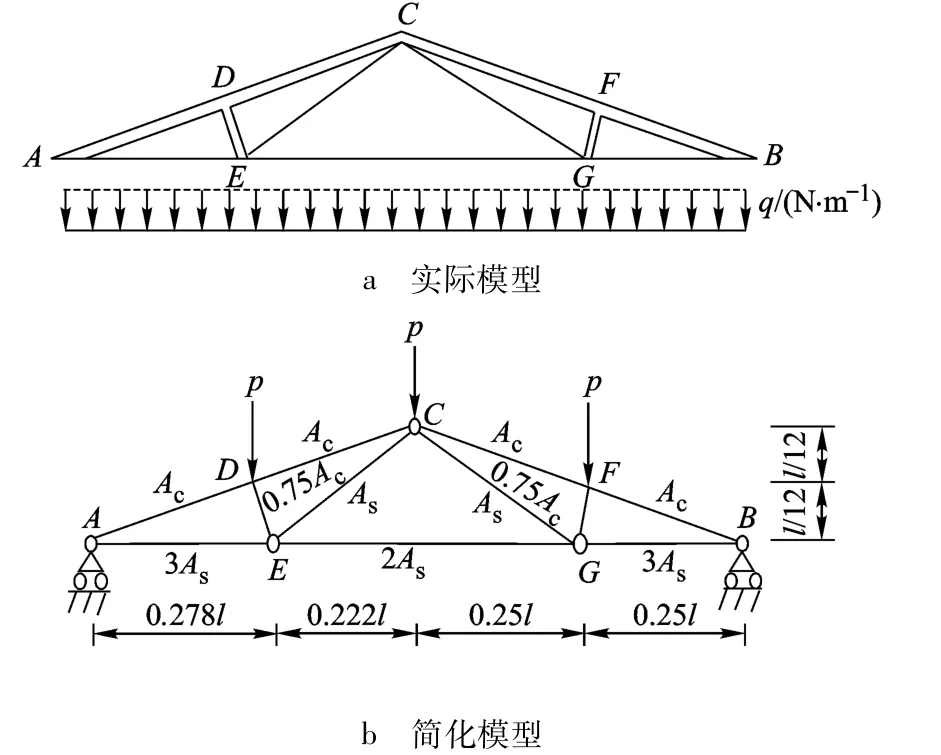
图3 屋架结构示意图

设C点沿垂直向下方向的位移为Δc，很显然Δc为随机变量的隐函数.约束C点的向下挠度不大于3 cm.根据约束条件建立功能函数为

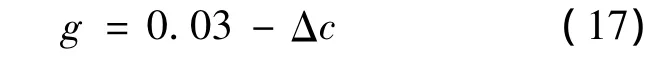
对随机变量按式(12)变化，利用有限元方法计算节点C在迭代点处的实际位移，根据本文方法模拟其极限状态曲面，将此类隐式功能函数的问题转化为显式问题.计算结果如表4所示，本文方法在精度上与MCS方法基本一致，相对误差仅0.97%，能更好的模拟响应曲面，进一步验证了此法的可行性、高效性.

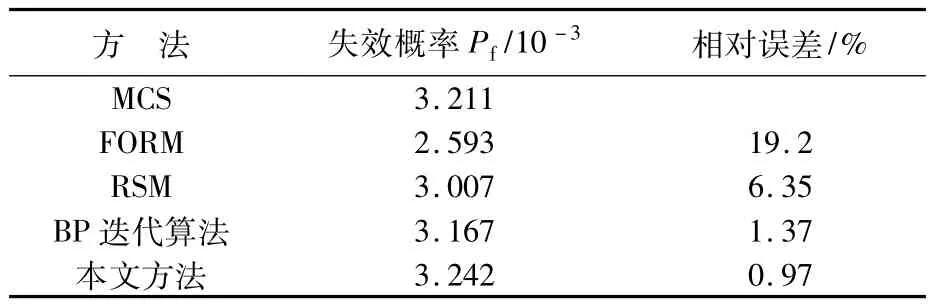
表4 算例3的失效概率计算结果

5 结论

基于多项式基函数神经网络的结构可靠性分析充分利用多项式基函数的逼近能力，以及神经网络在计算功能函数未知时的优越性.在神经网络求权值的过程中，利用激励函数广义逆矩阵的形式确定权值，避免传统BP网络梯度下降法带来的收敛速度慢和易陷入局部极小点的缺点.本文所提方法不仅思路简单，同时易于编程.通过算例分析，表明该方法的正确性与实用性.

References)

[1]张明.结构可靠度分析:方法与程序[M].北京:科学出版社，2009:8－9

Zhang Ming.Structural reliability analysis:methods and procedures[M].Beijing:Science Press，2009:8－9(in Chinese)

[2]贡金鑫.工程结构可靠度计算方法[M].大连:大连理工大学出版社，2003:3－6

Gong Jinxin.Computational methods for reliability of engineering structures[M].Dalian:Dalian University of Technology Press，2003:3－6(in Chinese)

[3]Wang Liping，Grandhi R V.Safety index calculation using intervening variables for structural reliability analysis[J].Computers and Structures，1996，59(6):1139－1148

[4]Kaymaz I，McMahon C A.A response surface method based on weighted regression for structural reliability analysis[J].Probabilistic Engineering Mechanics，2005，20(1):11－17

[5]Allaix D L，Carbone V I.An improvement of the response surface method[J].Structural Safety，2011，33(2):165－172

[6]李贵杰，吕震宙，赵新攀.基于加权线性响应面的结构可靠性估计的鞍点逼近方法[J].机械强度，2010，32(6):917－921

Li Guijie，Lü Zhenzhou，Zhao Xinpan.Saddle point approximation of structural reliability on weighted linear response surface method[J].Journal of Mechanical Strength，2010，32(6):917－921(in Chinese)

[7]Gomes H M，Awruch A M.Comparison of response surface and neural network with other methods for structural reliability analysis[J].Structural Safety，2004，26(1):49－67

[8]Elhewy A H，Mesbahi E，Pu Y.Reliability analysis of structures using neural network method[J].Probabilistic Engineering Mechanics，2006，21(1):44－53

[9]Deng Jian，Gu Desheng，Li Xibing，et al.Structural reliability analysis for implicit performance function using artificial neural network[J].Structural Safety，2005，27(1):25－48

[10]陆强华.基于径向基函数神经网络的结构可靠性分析[J].中国科技信息，2008，20(5):234－235

Lu Qianghua.Structural reliability analysis based on radial basis function neural network[J].China Science and Technology Information，2008，20(5):234－235(in Chinese)

[11]章兢，邹阿金，童调生.多项式基函数神经网络模型[J].湖南大学学报，1996，23(2):84－89

Zhang Jing，Zou Ajin，Tong Tiaosheng.A neural network based on polynomial basis functions[J].Journal of Hunan University，1996，23(2):84－89(in Chinese)

[12]曹飞龙，张永全，张卫国.单隐层神经网络与最佳多项式逼近[J].数学学报，2007，50(2):385－392

Cao Feilong，Zhang Yongquan，Zhang Weiguo.Neural networks with single hidden Layer and the best polynomial approximation[J].Acta Mathematica Sinica，2007，50(2):385－392(in Chinese)

[13]梁学章，李强.多元逼近[M].北京:国防工业出版社，2005:4－6

Liang Xuezhang，Li Qiang.Multivariate approximation[M].Beijing:National Defense Industry Press，2005:4 －6(in Chinese)

[14]吕震宙，杨子政，赵洁.基于加权线性响应面法的神经网络可靠性分析方法[J].航空学报，2006，27(6):1063－1067

Lü Zhenzhou，Yang Zizheng，Zhao Jie.An artificial neural network method for reliability analysis based on weighted Linear response surface[J].Acta Aeronautica Et Astronautica Sinica，2006，27(6):1063－1067(in Chinese)

[15]Ren Yuan，Bai Guangchen.New neural network response surface methods for reliability analysis[J].Chinese Journal of Aeronautics，2011，24(1):25－31