乏信息多传感器压力数据自助模糊融合估计

王中宇 王 倩

(北京航空航天大学 仪器科学与光电工程学院，北京100191)

付继华

(中国地震局地壳应力研究所，北京100085)

乏信息[1]是指测量数据具有的测量信息不完整和不充足.例如概率分布已知，但仅有几个数据用于数据处理;概率分布未知，测量数据也只有少量;趋势项未知等都可认为其具有乏信息特征.随着国防工业的发展，在航空、航天运载系统、载人航天工程系统、战术导弹、飞行姿态控制、遥感测量、武器装备及船舶制造等行业[2－4]压力传感器的使用比例较大.在这些领域的多传感器压力测量过程中，常出现测量次数较少，或者测量数据个数较少无法确定其概率分布等情况，因此乏信息特征存在于多传感器压力测量数据的融合估计过程中.

多传感器数据融合是一个具有不确定特征的复杂数据处理过程，融合方法作为研究的热点，一直受到人们的重视，这方面国内外已经作了大量的研究，并提出了许多融合方法[5].目前，这些方法大致可以分为两类:概率统计方法[6]和人工智能方法[7].概率统计方法发展相对成熟和系统化，其中卡尔曼方法[8]广泛应用于高斯分布的测量数据处理，贝叶斯估计[9]在分布未知的测量数据融合中具有优越性.人工智能又可分为逻辑推理方法和学习方法，逻辑推理属于不确定性推理，对信息的表示和处理更加接近人类的思维方式，但是对信息的描述存在很大的主观因素，对信息的表示和处理缺乏客观性;学习方法目前包括神经网络，映射学习方法，数据挖掘等[10－12]，学习方法自身理论方面还不够完善，存在稳定性问题、泛化能力、缺乏有效的学习机制等.

以上所提研究方法从不同方面实现了多传感器数据的融合，在很大程度上丰富和发展了多传感器数据融合理论.人工智能方法与基于大数定律与中心极限定理的统计学方法，在测量数据概率分布未知或测量数据个数较少的乏信息条件下具有一定的局限性.近年来，自助法[13]，模糊数学理论[14]，灰色系统理论[15]等方法在处理乏信息问题上有一定应用.如文献[14]中应用模糊数学理论实现了乏信息测量参数的有效估计;文献[16]成功将自助法应用到多传感器滑坡时间序列融合;文献[15]运用灰自助法实现了乏信息虚拟仪器测量不确定度的评定.但这些方法在多传感器压力测量数据融合估计问题中尚未应用.

本文通过自助法对测量数据进行重复抽样，增加测量数据的样本量，进行多传感器压力测量数据融合，并利用模糊隶属函数实现了压力测量数据真值与区间估计.

1 自助模糊数据融合估计原理

自助模糊数据融合估计方法是将自助法[16]与模糊隶属函数[14]的概念有机地结合起来，进行数据分析的一种本征融合方法.图1为原理图.

1.1 多传感器压力测量数据自助融合

在多传感器压力测量过程中，设小样本空间的s个压力传感器获得的测量数据时间序列为初始序列Z为

图1 乏信息自助模糊融合估计原理

式中，zm(k)为第m个压力传感器获得的第k个数据;k为时间;n为数据量.

在时间k，s个压力传感器测量数据为

依据自助抽样原理[15]，在中自助抽样，获得B个自助仿真样本:

式中，zk，b(u)为时间k的第b个自助样本中的第u个数据.

Zkb中每列的均值为

式中，nd为第d组的数据量.

将式(2)中离散值zm(k)替换为连续变量x，依据最大熵算法[15]，得自助分布概率密度函数p(x).

在时间k，s个压力传感器测量数据融合值用数学期望表示为

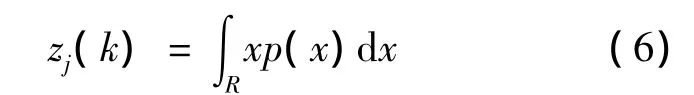
式中，R为积分空间.

式(6)可以用离散形式表示为加权均值:

式中，Zd为第d组的组中值.

对于s个压力传感器测量数据，zj(k)构成一个时间融合序列，即自助融合序列Zj，用矩阵表示为

1.2 多传感器压力测量数据模糊估计

在模糊数学中，将离散数x(k)看作模糊数，连续的x即为模糊变量.

如图2所示，x的隶属函数定义:

式中，f(x)∈[0，1]为隶属函数;f1(x)为左增函数;f2(x)为右减函数;X0为测量参数总体分布的估计真值;[XL，XU]为在最优水平λ下的估计区间;XL为区间下限;XU为区间上限.

图2 模糊隶属函数图

将Zj序列按升序排序，形成新序列Y={y(1)，y(2)，…，y(n)}.定义:

设线性隶属函数:

式中，i=1，2，…，n－1.

则满足区间[0，1]的测量数据模糊隶属离散值为

取最大mi对应的y(i)为真值X0的估计真值Xv，对应的序号i为v.

用下面两个多项式拟合模糊隶属函数:

分别逼近离散值f1j(y(j))和f2j(y(j)).设

根据模糊集合理论意义上的最优水平λ，在模糊集合理论意义上，取λ= 0.5(λ∈[0，1]).确定相应的水平截集，得到乏信息多传感器压力测量数据的估计隶属区间.可由下面两式得XL和XU:

2 实例分析

为了说明算法的有效性，本文分别在乏信息和大样本两个条件下进行实验验证.

2.1 乏信息实验分析

选取某压力测量系统的4个检测点压力传感器获得的压力值的时间序列数据Y1～Y4见表1.分别利用本文提出的自助模糊算法、多模型跟踪法[17]以及均值融合法，进行乏信息多传感器压力测量数据融合估计.在本次实验中，取m=4，n=11，Y={Y1，Y2，Y3，Y4}，B=1000.自助模糊法，多模型跟踪法和均值融合法的融合序列如表2中F1，F2，F3所示.根据模糊隶属函数得估计真值X0与区间[XL，XU]，见表2.

表1 乏信息多传感器压力测量数据原始时间序列

在本实验中，进行数据融合对比分析，据表2，F1和F2的数据接近，均能综合反映该测量过程的演化情况.图3描述了原始测量数据序列与自助融合序列.由图3可得，本文算法所得融合序列与原始测量数据的变化趋势接近，能够精确地描述和反映测量系统的状态.为了对算法的性能分析，本文利用区间分析对测量数据进行了检验，区间估计精度如图4所示.由图4可得，自助模糊模型区间判定的精度为87%，其次多模型跟踪法为82%，均值融合仅能达到57%.由此数据可以看出，在乏信息条件下，自助模糊模型能够有效地实现多传感器测量数据融合，融合过程中对测量数据个数及其分布规律都没有要求.

表2 乏信息多传感器压力测量数据融合序列

图3 融合对比图

图4 区间估计精度图

2.2 大样本仿真实验分析

在大样本量的情况下，为考核融合估计效果，定义置信水平P下的波动范围为

定义对波动范围真值U0估计的相对误差(绝对值)为

在置信水平P下，误报率PE为

式中，e为位于估计区间U外数据;n为乏信息子样本数据总数.

可靠度Pr为

本文选取正态分布的测量数据进行仿真实验，设定特征参数为标准差σ=0.1和真值X0=52，仿真出N=1024个数据x(k).仿真出的1024个数据可以被认为是大样本测量数据.用统计法进行估计，得到此组大样本数据的σ=0.0977.取P=99.73%，得到波动范围的约定真值U0=6σ=0.5862.

在此样本数据序列中，抽取乏信息子样本，从这1024个数据中抽4组数据，每组数据个数为n=10个，构成数据序列C1～C4，对这4组数据，应用自助模糊方法与统计方法进行融合估计，结果如表3所示.

由表3可知，在乏信息条件下，相较于统计方法，自助模糊方法的融合估计结果与约定真值差异较小.数据表明:自助模糊方法可以很好地实现具有乏信息特征的测量数据融合估计.自助模糊估计较大样本约定真值的相对误差为10%左右，接近于真实的测量数据，在P为99.7%下，区间估计的Pr可达95%，说明此方法可以较为准确地描述测量系统的特征参数，反映测量过程的真实情况.

表3 仿真实验结果对比

3 结论

依据乏信息多传感器压力测量数据融合估计问题的特征，本文提出了乏信息多传感器压力测量数据自助模糊融合估计模型，拓展了融合估计方法的条件限制，并通过实际测量数据进行验证.其中，自助抽样对样本量进行扩充，允许原始测量数据个数有限，而且对数据的概率分布无任何要求;模糊估计实现最少仅需3个数据而且同样无需测量数据概率分布信息.实验表明:在乏信息条件下，算法精度可达87%;在大样本条件下，测量数据在置信水平99.7%下，融合估计可靠性可达95%，所以自助模糊融合估计模型，能利用少量的测量数据对具有乏信息特征的压力传感器测量数据的测量真值与区间进行有效估计，从而全面地掌握被测量的真实情况，最大限度的避免漏报、误报.通过算例有效地验证了自助模糊融合估计模型的可行性和科学性.

References)

[1]葛乐矣，赵伟，徐子帆，等.乏信息动态测量误差灰自助预报[J].农业机械学报，2011，42(7):210－214，219

Ge Leyi，Zhao Wei，Xu Zifan，et al.Error predicting for dynamic measurement of poor information based on grey bootstrap method[J].Transactions of the Chinese Society for Agricultural Machinery，2011，42(7):210－214，219(in Chinese)

[2]Seiler F，Srulijes J.New results in numerical and experimental fluid mechanics IV[M].Germany:Springer-Verlag Berlin and Heidelberg GmbH＆co K，2004:87，124－131

[3]Kotomin A A，Shirokova N P，Dushenok S A，et al.Detonation pressure of explosive charges applied in spacecraft division systems[J].Solar System Research，2011，45(7):677－683

[4]Tao Zui，Qin Bangyong，Li Ziwei，et al.Satellite observations of the partial pressure of carbon dioxide in the surface water of the Huanghai sea and the Bohai sea[J].Acta Oceanologica Sinica，2012，31(3):67－73

[5]Khaleghi B，Khamis A，Karray F O，et al.Multisensor data fusion:a review of the state of the art[J].Information Fusion，2013，14(1):28－44

[6]Chen Yukun，Si Xicai，Li Zhigang.Research on Kalman-filter based multisensor data fusion[J].Journal of Systems Engineering and Electronics，2007，18(3):497－502

[7]Noureldin A，El-Shafie A，Taha M R.Optimizing neuro-fuzzy modules for data fusion of vehicular navigation systems using temporal cross-validation[J].Engineering Applications of Artificial Intelligence，2007，20(1):49－61

[8]Deng Zili，Zhang Peng，Qi Wenjuan，et al.Sequential covariance intersection fusion Kalman filter[J].Information Sciences，2012，189:293－309

[9]Zhu Hao，Henry Leung，He Zhongshi.A variational Bayesian approach to robust sensor fusion based on Student-t distribution[J].Information Sciences，2013，221:201－214

[10]Caron F，Davy M，Duflos E，et al.Particle filtering for multisensor data fusion with switching observation models:Application to land vehicle positioning[J].IEEE Transactions on Signal Processing，2007，55(6Part 1):2703－2719

[11]Noureldin A，Osman A，El-Sheimy N.A neuro-wavelet method for multi-sensor system integration for vehicular navigation[J].Measurement Science＆Technology，2004，15(2):404－412

[12]Vega J，Pereira A，Portas A，et al.Data mining technique for fast retrieval of similar waveforms in Fusion massive databases[J].Fusion Engineering and Design，2008，83(1):132－139

[13]Xia Xintao，Chen Xiaoyang，Zhang Yongzhen，et al.Grey bootstrap method of evaluation of uncertainty in dynamic measurement[J].Measurement，2008，41(6):687－696

[14]Wang Qian，Fu Jihua，Wang Zhongyu，et al.A seismic intensity estimation method based on the fuzzy-norm theory[J].Soil Dynamics and Earthquake Engineering，2012，40:109－117

[15]Ge Leyi，Wang Zhongyu.Novel uncertainty-evaluation method of virtual instrument small sample size[J].Journal of Testing and Evaluation，2008，36(3):273－279

[16]夏新涛，陈晓阳，张永振，等.多传感器滑坡时间序列的自助融合及其灰假设检验[J].岩土力学与工程学报，2007，26(9):1904－1912

Xia Xintao，Chen Xiaoyang，Zhang Yongzhen，et al.Bootstrap fusion and its grey hypothesis testing for landslide time series of multi-sensor[J].Chinese Journal of Rock Mechanics and Engineering，2007，26(9):1904－1912(in Chinese)

[17]郭科，彭继兵，许强，等.滑坡多点数据融合中的多传感器目标跟踪技术应用[J].岩土力学，2006，27(3):479－481

Guo Ke，Peng Jibing，Xu Qiang，et al.Application of multi-sensor target tracking to multi-station monitoring data fusion in landslide[J].Rock and Soil Mechanics，2006，27(3):479－481(in Chinese)