基于激励解耦法的汽车动力总成悬置系统优化设计

张兴川

Zhang Xingchuan（安徽省汽车产品质量监督站，安徽 合肥 230051）

0 引 言

随着道路条件的改善和汽车设计的轻量化，发动机成为汽车中的最大振源，动力总成悬置系统作为发动机和车身之间的隔振系统，其性能设计优劣直接影响整车的NVH性能[1]。以往对动力总成悬置系统进行研究时，大多是假设动力总成直接连接到地面上，只考虑动力总成 6自由度模型，未考虑整车其他部分，如副车架、车身、悬架以及车轮等其他弹性基础对其性能的影响[2-3]。实际上，动力总成悬置系统处于整车复杂的多自由度系统中，与其他子系统存在着耦合作用[4-5]。

文中在对动力总成悬置系统进行优化设计时考虑了底盘系统的影响，根据解耦应该与某一特定的激励有关的理论，以某国产轿车为例，运用改进的遗传算法，通过使能量解耦度在转矩轴方向和垂直方向最大化来寻找悬置系统的最优参数。

1 动力总成与底盘系统耦合模型

悬置系统的研究并不是一个独立过程，需要考虑到与其他系统的耦合。文中考虑到动力总成和底盘之间的相互作用，建立动力总成和底盘系统的耦合振动模型，如图1所示。

将动力总成和底盘分别看作6自由度的刚体，位移分别为沿x、y、z轴的平动和绕x、y、z轴的转动；每个车轮只考虑1个垂直方向的自由度（za1，za2，za3，za4），因此整个耦合系统共有 16个自由度。根据两系统的耦合作用，不考虑施加到底盘上的激励，可建立动力总成和底盘系统的耦合运动方程

其中，M为质量矩阵；C为阻尼矩阵；K为刚度矩阵（下标1代表动力总成，2代表底盘）；F1为作用在发动机上的激励；K12，K21分别为动力总成和底盘系统间相互耦合作用的刚度矩阵；C12，C21分别为动力总成和底盘系统间相互耦合作用的阻尼矩阵。

2 动力总成悬置系统参数优化设计

2.1 目标函数的建立

解耦应该与某一特定的激励有关，一方面，发动机燃烧的爆发力会引起曲轴扭振，尤其在发动机怠速时，扭振激励的频率与悬置的频率接近，因此这种模态下的解耦是必要的；另一方面，气缸方向上的内部力以及相关运动也是发动机的主要激励之一，因此对其垂直方向的解耦性也有较高要求，其他振型的固有频率控制在一定范围内即可。因此，建立目标函数如下：

其中，Tθy，Tz分别为系统在转矩轴和垂直方向上的能量解耦度[5]。

2.2 设计变量

悬置的位置、各向刚度和安装角度等的改变均会引起目标函数值的变化。由于所设计悬置的安装方式为平置式，故取悬置位置和各向刚度为设计变量。

2.3 约束条件

1）动力总成各阶固有频率通常可确定在 6～17 Hz之间，以避开其他总成的固有频率。

2）动力总成绕曲轴方向转动的固有频率应小于发动机怠速时激励频率的1/2。

3）对于普通橡胶悬置，因为材料与工艺原因，压剪刚度比值（压剪比）L应在3～8之间。

4）为了增加支承的使用寿命，需要保证动力总成的最大位移量不得超过10 mm，悬置侧向变形不得超过2 mm。

综上所述，得到动力总成悬置优化设计的数学模型

2.4 优化方法

在算法上选择表现优异的非支配排序的遗传算法[6]（NSGA-II），并对其进行进一步的改进，采用改进后的算法求得悬置参数组合的最优解。改进后的算法流程，如图2所示。运行时的参数为：最大代数为100，种群规模为100，采用十进制编码，杂交概率为0.8，变异概率为0.07。

3 计算实例

3.1 优化前后解耦效果的比较

以某4缸发动机三点橡胶悬置系统（后悬置为上下体）为研究对象。其怠速转速为750 r/min，动力总成质量m=214.77 kg，转动惯量{Ix Iy Iz Ixy Iyz Izx} = {14.326.612.76 -1.42-0.081.65}（kgm2），各悬置点的坐标和刚度如表1所示。

分别计算优化前后的动力总成悬置系统的固有频率和能量解耦度，如表2和表3所示。可知，相比原系统，优化后系统的各方向解耦度有了很大提高，解耦度均达到 90%以上，其中垂直方向和绕转矩轴方向分别达到94.0%和96.8%。并且各方向的频率分布合理，垂直方向频率为9.74 Hz，避开了前桥与车身的垂直固有频率。绕曲轴方向频率为 11.5 Hz，小于发动机怠速时激励频率的，可以达到很好的隔振效果。

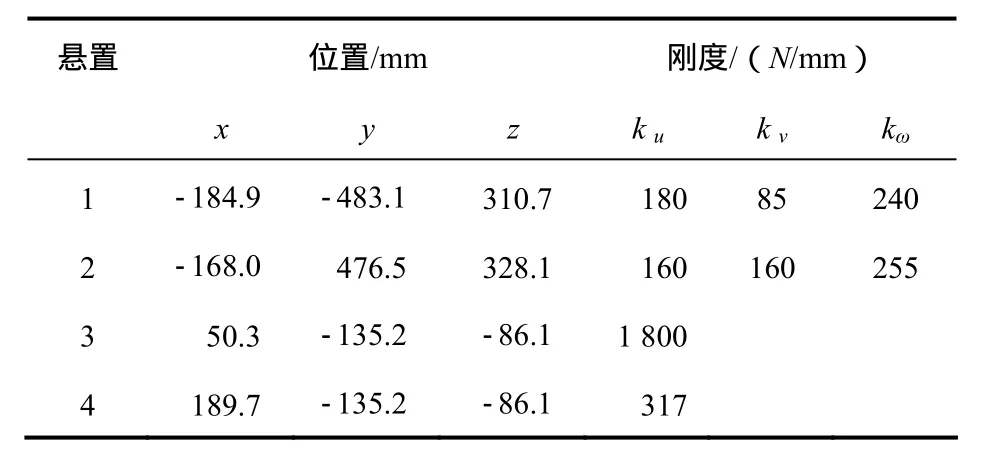
表1 动力总成各悬置参数

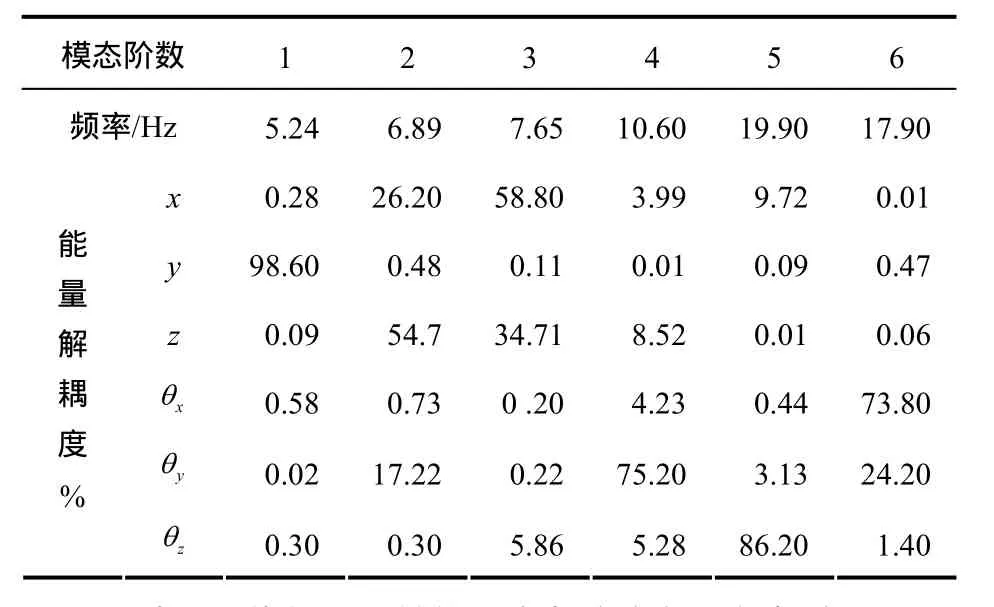
表2 优化前系统的固有频率和能量解耦度

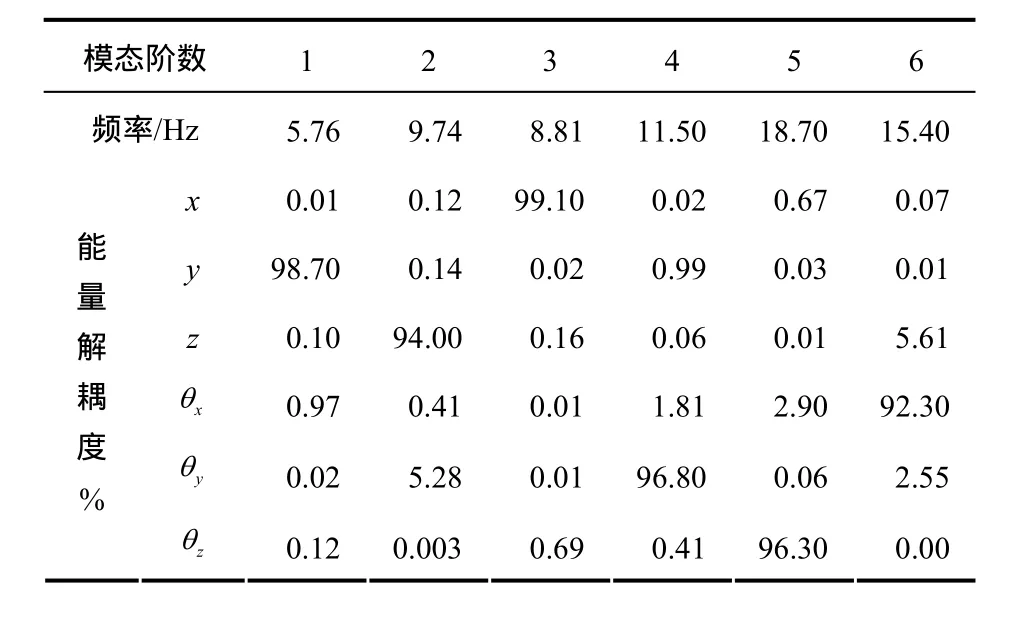
表3 优化后系统的固有频率和能量解耦度

3.2 整车仿真验证

悬置系统优化的最终目标是减小车身上关键点的振动，考察优化后的悬置系统在整车背景下的隔振效果才最有意义。采用有限元法和多体动力学方法建立整车刚柔耦合模型，并利用轮胎路面工具箱建立轮胎和路面模型，如图 3所示。通过计算各工况发动机激励作用下优化前后整车上关键点的振动响应，以此预测优化后悬置系统在整车上的隔振效果。

在整车上，取驾驶员座椅下地板A点、副驾驶座椅下地板B点、左侧B柱座椅下地板C点、方向盘上的D点等作为振动关键点。由于篇幅限制，仅以不同工况时，转向盘的振动情况为例进行悬置系统优化效果的评价。行驶工况为B级路面，分别计算Ⅲ挡工况下以 80 km/h的车速行驶时，和Ⅴ挡工况下以60 km/h的车速行驶时，悬置优化前后转向盘中心的垂向振动情况，优化前后的振动加速度曲线分别如图4和图5所示。可知，优化后的系统中，转向盘垂向的振动加速度比优化前有了明显降低。由此可以看出，采取的优化方案是可行的。

4 结束语

针对悬置系统与其他系统存在耦合作用的问题，建立了动力总成悬置系统与底盘系统的耦合模型。并根据解耦应该与某一特定的激励有关的理论，结合发动机的主要激励，以在转矩轴方向和垂直方向的能量解耦度最大为目标，应用改进的非支配排序遗传算法对各悬置的位置和刚度进行优化，并将优化前后系统的固有频率和能量解耦度进行了对比。建立了整车模型，分析了整车中悬置优化前后转向盘中心的振动情况，结果表明优化后的悬置系统降低了整车的振动，提高了隔振性能，为动力总成悬置系统在整车中的设计提供了参考。

[1]Yu Y.H，Nagi G Naganathan，Rao V. Dukkipati. A literature review of automotive vehicle engine mounting systems [J]. Mechanism and Machine Theory，2001，36（1）：123-142.

[2]Jeong T，Singh R. Analytical Methods of Decoupling the Automotive Torque Roll Axis. Journal of Sound and Vibration，2000，234（1）：85-114.

[3]阎红玉，徐石安. 发动机—悬置系统的能量法解耦及优化设计[J]. 汽车工程，1993（6）：321-328.

[4]胡金芳，陈无畏.基于弹性支撑的汽车动力总成悬置系统解耦研究[J]. 中国机械工程，2012，23（23）：2879-2885.

[5]Courteille E，Léotoing L，Mortier F，et al. New analytical method to evaluate the powerplant and chassis coupling in the improvement vehicle NVH [J]. European Journal of Mechanics A/Solids，2005，24（6）：929-943.

[6]高媛. 非支配排序遗传算法（NSGA）的研究与应用[D]. 浙江大学，2006.