亚轨道飞行器发动机故障下飞行程序设计方法
2013-11-04王文虎李新国王晨曦
王文虎, 李新国, 王晨曦
(1.西北工业大学 航天学院, 陕西 西安 710072; 2.中北大学 机电工程学院, 山西 太原 030051)
亚轨道飞行器发动机故障下飞行程序设计方法
王文虎1,2, 李新国1, 王晨曦1
(1.西北工业大学 航天学院, 陕西 西安 710072; 2.中北大学 机电工程学院, 山西 太原 030051)
针对亚轨道飞行器单台发动机发生故障情况,提出了基于正指数攻角的发动机故障下飞行程序设计方法,给出了不同故障时刻的仿真结果,并与正常飞行情况进行了比较。仿真结果表明,对于不同故障时刻,该方法均能够在满足弯矩约束、攻角限制的情况下使得故障飞行器安全到达预定高度,为后续应急返回机动飞行提供有利的飞行条件。
亚轨道飞行器; 发动机故障; 飞行程序设计
0 引言
亚轨道飞行器(SRLV)是一种在亚轨道空间作业、可重复使用的多用途跨大气层飞行器,可以适应多样化任务需求,具有广泛的应用前景[1]。亚轨道飞行器上升段飞行环境及动力学特性与运载火箭大气层飞行段类似,因此,可以借鉴运载火箭的弹道设计方法。
飞行程序是指运载火箭主动段飞行时俯仰角的变化规律,飞行程序设计是运载火箭弹道设计的重要组成部分,一些重要的性能指标,如运载能力、入轨精度以及飞行过载和受热情况等都与飞行程序设计密切相关[2]。特别是在发动机故障下,如何设计上升段飞行程序对任务安全性尤为重要。文献[3-6]分别针对不同研究对象(亚轨道飞行器、机载运载火箭、小型运载火箭以及速燃弹道导弹)给出了相应的飞行程序设计方法,但发动机故障下飞行程序设计方法研究目前还较为少见。
本文针对亚轨道飞行器单台发动机发生故障情况,提出了基于正指数攻角的发动机故障下飞行程序设计方法,给出了不同故障时刻的仿真结果,并与正常飞行情况进行了比较。
1 正常情况下飞行程序设计
亚轨道飞行器上升段飞行程序设计不仅要从弹道的观点考虑(如减少速度损失),而且还要考虑到飞行器结构强度、控制和发射使用方面的许多实际约束条件。飞行程序设计时应尽量减小重力以及气动力引起的速度损失,同时减小作用在飞行器上的气动载荷。
类似于传统的一次性运载火箭,亚轨道飞行器上升段可分为垂直上升段、转弯段和瞄准段[2]。无故障时飞行程序设计可以采用负指数攻角方案或抛物线俯仰角方案来进行程序角设计。尽管采用抛物线俯仰角方案具有设计变量少的优点[5],但采用负指数攻角方案在处理攻角限制以及弯矩约束时更为直观简单。因此,选用负指数攻角方案对正常飞行时的飞行程序进行设计。
转弯段攻角变化规律为:
α(t)=-4αmZ(1-Z)
(1)
Z=e-a(t-t1)
(2)
式中,αm为上升段负攻角绝对值的最大值,a为选取的某一常值,这两个参数均为设计参数;t1为垂直上升段结束时刻。由式(1)所描述的转弯段攻角变化规律如图1所示。

图1 正常飞行负指数攻角变化曲线Fig.1 Negative exponential angle of attack profile for nominal case
飞行中必须对攻角的大小进行一定的限制。采取的限制条件为:
|α|≤10°
(3)
为了满足弯矩约束,需要对qα进行限制,以限制法向过载的大小,从而保证弯矩处于结构载荷所允许的范围内:
|qα|<|qα|max=1 300 (N/m2·rad)
(4)
2 发动机故障下飞行程序设计
由于发动机故障模式较多,限于篇幅,本文只针对单台发动机故障关机情况进行研究。单台发动机故障下,保证飞行器能够在加速能力与控制能力均下降的情况下,安全到达返回窗口是故障下飞行程序设计的首要任务。因此其设计目的是在满足弯矩、攻角限制等约束条件下,使亚轨道飞行器尽可能快地飞过最大动压区,到达较高的飞行高度,因为较高的飞行高度意味着动压较低,低动压环境有利于进行较大的机动飞行来对准目标着陆场。同时为了有利于后续制导方法对弹道倾角的调整,程序飞行末端弹道倾角不能够太大。后面研究中预设飞行高度为40 km。
2.1 负指数攻角方案
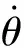
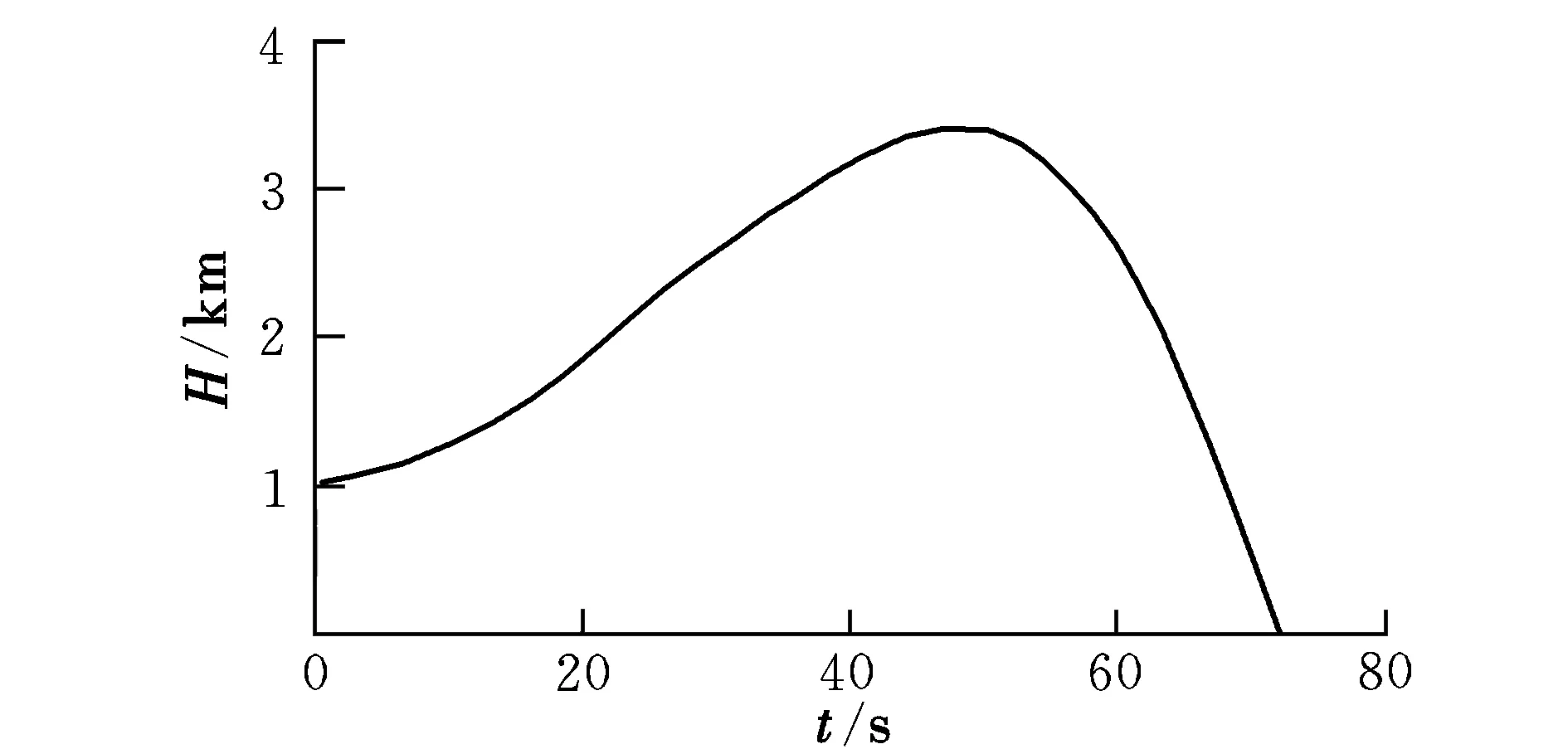
图2 高度变化曲线Fig.2 Altitude vs time for flight program
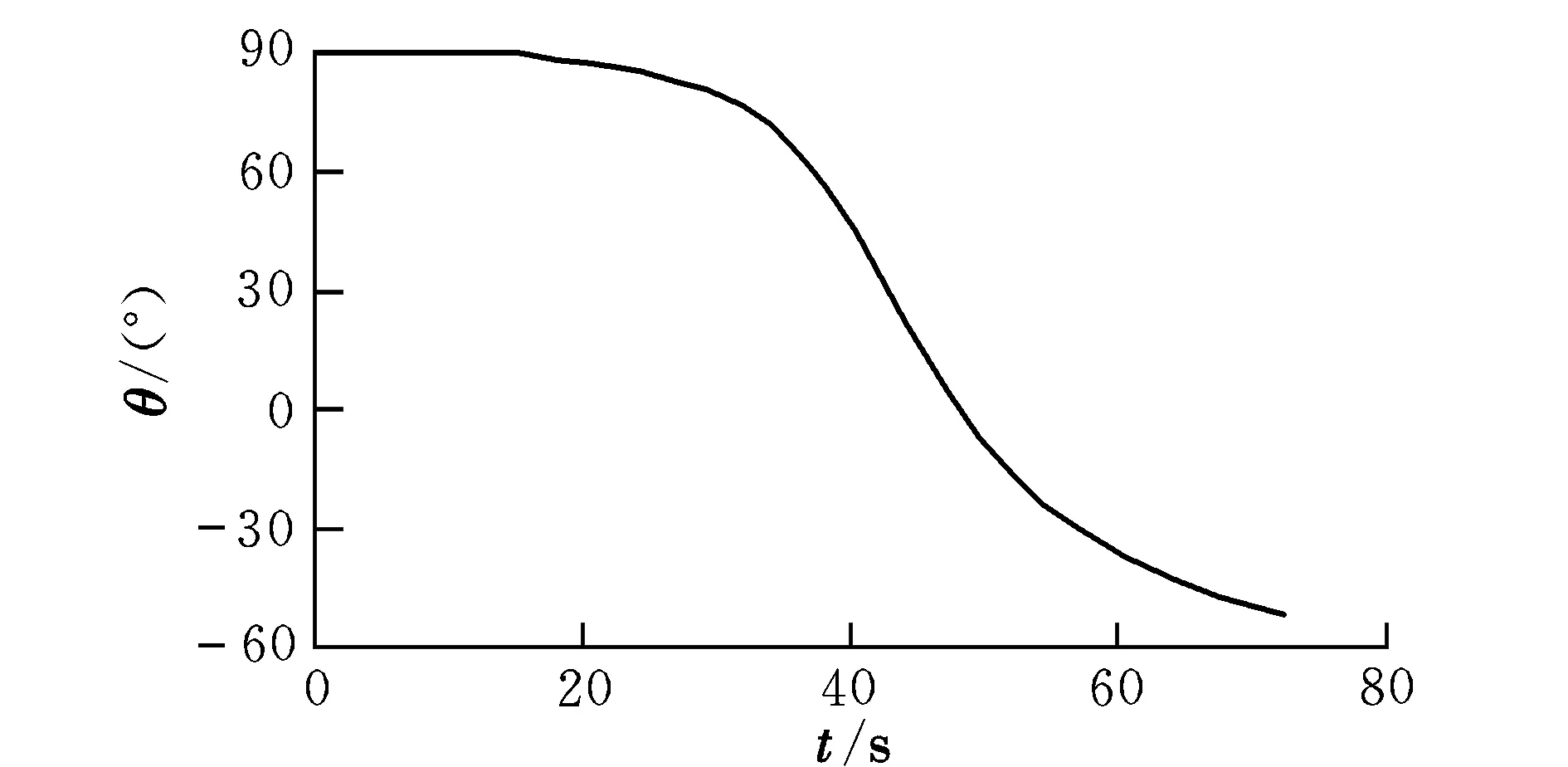
图3 弹道倾角变化曲线Fig.3 Flight path angle vs time for flight program
2.2 正指数攻角方案
考虑到故障后首先需要正攻角飞行来减缓弹道下降速度,同时为了保证弯矩约束能够满足要求,应在气动力急剧变化的最大动压区前使攻角收缩为零或较小值,以减少气动载荷和气动干扰。因此,提出了故障下基于正指数攻角的飞行程序设计方法。故障后攻角变化规律如图4所示。
发生故障前为正常飞行情况,采用原负指数攻角形式设计飞行程序,故障后攻角变化规律为:
α(t)=4α1mZ(1-Z)
(5)
式中,Z=e-a1(t-tfail),其中tfail为发生故障时刻,a1为选取的某一常值。

图4 正指数攻角变化曲线Fig.4 Positive exponential angle of attack profile
图中,α1m为正攻角的最大值。α1m,a1可作为设
计参数,α1m值越大则弹道转弯越慢,a1越大则到达最大攻角越早,通过调整α1m和a1就可以调整弹道转弯的快慢。
3 仿真结果与分析
采用提出的发动机故障下正指数攻角方案进行飞行程序设计,并仿真到某一给定飞行高度40 km时结束,末端弹道倾角取正常飞行时40 km所对应的弹道倾角23°。由于发动机故障下控制能力下降,为了有利于飞行控制,仿真中最大攻角绝对值取值不超过5°。不同故障时刻仿真结果如图5所示。
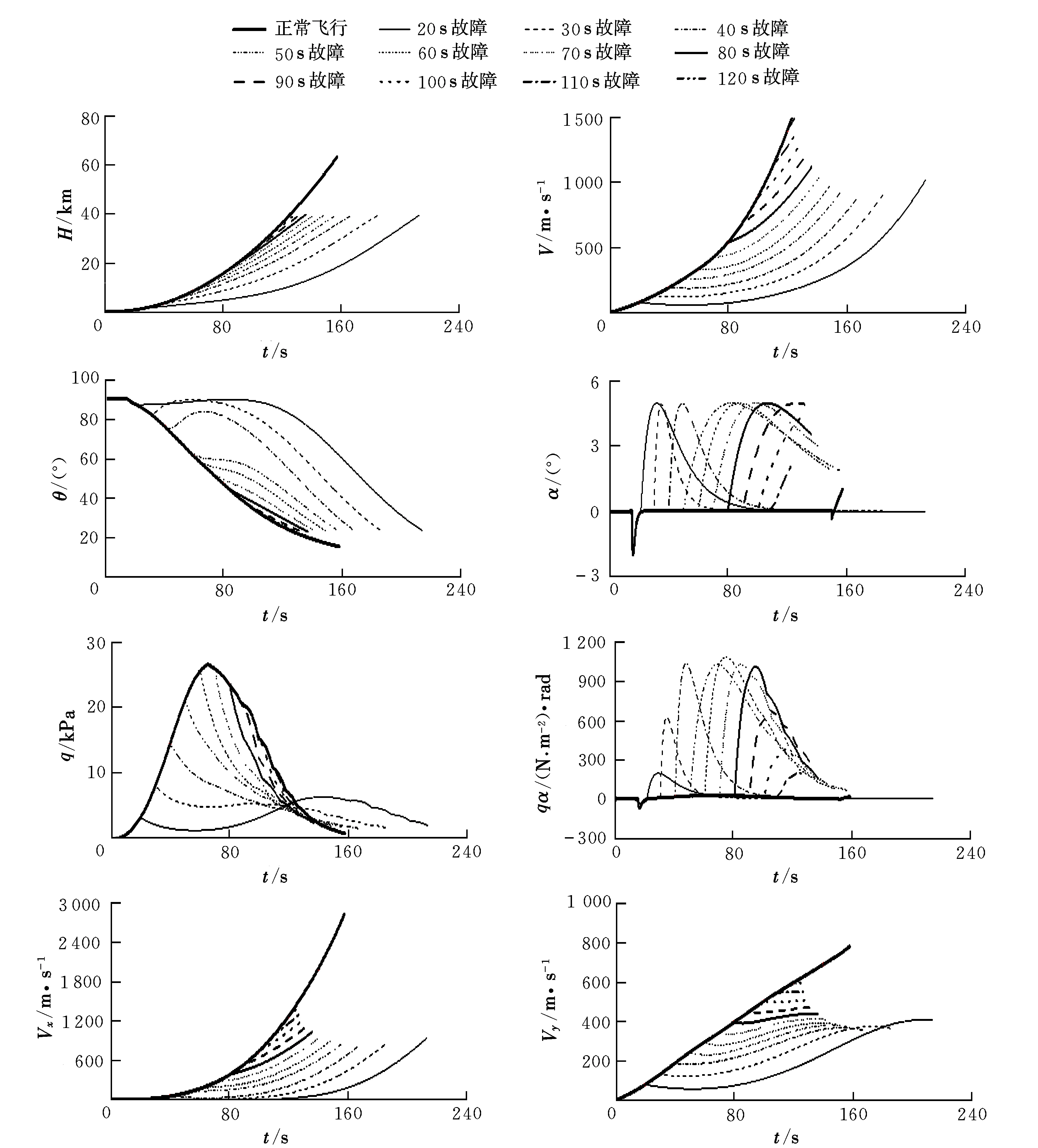
图5 不同故障时刻仿真曲线Fig.5 Simulation results for different fault time
从仿真结果可以看出,不同故障时刻采用正指数攻角方案均可以在满足弯矩约束、攻角限制的情况下到达预定高度40 km,末端弹道倾角23°。若故障发生较早(20 s~40 s),推重比较小,速度分量Vy较低,必须快速地增大攻角,使得弹道转弯速度不至于太快。由于此时动压较低,因此快速地增大攻角不会导致违背弯矩约束;若故障发生在最大动压区(40 s~90 s),此时动压较大,为了能够满足弯矩约束,攻角不能增加太快,需要调小设计参数a1来推后最大攻角到来的时刻,尽管处于最大动压区,但发动机故障会导致动压降低,因此也可以采用比正常情况更大的攻角飞行,但从弯矩曲线图可以看出,攻角上调幅度有限,如攻角太大,有可能使得弯矩约束不能满足要求,如果选择较小的攻角则不能尽快地飞出稠密大气层,同时从速度曲线图可以看出,由于处于最大动压区,大攻角飞行必然会带来更大的速度损失;若故障发生较晚(90 s~120 s),此时已经飞过最大动压区,具有一定的飞行高度并且推重比较大,因此设计参数的选取受弯矩约束影响很小,只需要适当地增大攻角就可以满足终端约束。
图6给出了设定最大攻角α1m=5°时,不同故障时刻的飞行程序设计参数a1值。
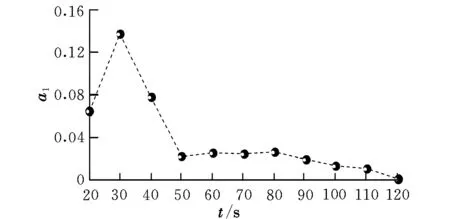
图6 不同故障时刻设计参数a1值Fig.6 Design parameter a1 for different fault time
4 结束语
本文提出了基于正指数攻角的飞行程序设计方法,用于亚轨道飞行器发动机故障下大气段飞行程序设计。尽管所提出的正指数攻角方案能够满足设计要求,但参数调节不够灵活,针对不同故障时刻都需要繁琐的参数调整来满足弯矩约束以及终端约束,因此下一步研究需要寻求一种能够减少参数调整次数的故障下飞行程序设计方法。
[1] Martin J C,Law G W.Suborbital reusable launch vehicles and applicable markets[R].SB1359-01-Z-0020,2002.
[2] 贾沛然,陈克俊,何力.远程火箭弹道学[M].长沙:国防科学技术大学出版社,1993.
[3] 徐方暖,唐硕,闫晓东.亚轨道飞行器上升段制导方法研究[J].飞行力学,2008,26(5):36-39.
[4] 郑晓龙,唐硕.机载运载火箭飞行程序设计及仿真[J]. 计算机仿真, 2011,28(5):43-46.
[5] 杨希祥,江振宇,张为华.小型运载火箭大气层飞行段飞行程序设计研究[J].飞行力学,2010,28(4):68-72.
[6] 郝磊,李邦杰,王明海.速燃弹道导弹飞行程序角设计方法[J].弹箭与制导学报,2008,28(2):180-182.
(编辑:方春玲)
Flightprogramdesignforsuborbitalreusablelaunchvehicleafterenginefailure
WANG Wen-hu1,2, LI Xin-guo1, WANG Chen-xi1
(1.College of Astronautics, NWPU, Xi’an 710072, China; 2.College of Mechatronic Engineering, North University of China, Taiyuan 030051, China)
A method of flight program design is proposed for ascent trajectory design after engine failure of suborbital reusable launch vehicle. The ascent flight program was designed in positive-index angle of attack. Some trajectories of atmosphere flight stage in different failure instants were simulated, and compared with nominal case. The final results show that the method works well, and can safely guide fault SRLV to the scheduled height, and simultaneously meets various constrains such as structure constrains and limits of angle of attack.
suborbital reusable launch vehicle (SRLV); engine failure; flight program design
V412.4
A
1002-0853(2013)04-0359-04
2012-10-22;
2013-03-22; < class="emphasis_bold">网络出版时间
时间:2013-06-06 12:25
国家863计划基金项目
王文虎(1978-),男,山西代县人,讲师,博士研究生,研究方向为飞行器轨迹优化与制导。
