一种基于BFGS算法的二次规划控制分配算法

张宁, 章卫国, 李广文

(西北工业大学 自动化学院, 陕西 西安 710129)

一种基于BFGS算法的二次规划控制分配算法

张宁, 章卫国, 李广文

(西北工业大学 自动化学院, 陕西 西安 710129)

针对多操纵面飞行器的控制分配问题,提出了一种基于BFGS算法的控制分配策略。该分配策略克服了不动点迭代算法分配时舵面容易饱和的缺点。为验证BFGS分配策略的可行性和有效性,以某型战斗机为研究对象,进行了控制分配和重构仿真。仿真结果表明,该分配策略能将飞行指令在舵面饱和范围内合理地分配在各个舵面上。

飞行控制; 控制分配; 不动点迭代法; BFGS算法

0 引言

随着现代航空技术的发展,第四代战斗机对隐身性、超声速巡航、高机动性和敏捷性等多方面性能提出了更高的要求。在这种背景下,采用先进高效的多操纵面气动布局已经成为未来战斗机和其他飞行器的发展方向,因此现代战斗机普遍采用了多操纵面气动布局。这导致飞机操纵面的控制和组合方式不再唯一,从而产生了控制分配问题。

近年来,为了将飞行指令合理、有效地分配到各个操纵面上,科研人员提出了多种控制分配方法[1],如直接几何法、伪逆法、串接链法[2]、规划型算法等。直接几何法意义明确,可以实现在整个转矩可达集内求解,但是算法复杂,实时性差;伪逆法和串接链法运用得最为广泛,但是它们没有考虑操纵面的饱和限制,容易引起舵面饱和,并且分配效率低下,无法充分发挥多操纵面飞机的先进气动布局优势；规划型算法可以在整个转矩可达集内搜索最优解,能充分发挥飞机的气动潜能。

BFGS 算法[2]是一种基于牛顿迭代法的改进算法,它具有二阶收敛速度、自适应度高、收敛性好以及计算量小的特点,适合解决控制分配问题。本文将控制分配问题转化为二次规划问题加以求解[3],二次规划问题常用不动点法进行求解,虽然不动点法可以通过简单迭代来求解二次规划,但是不动点法迭代结果对初值敏感,并且所得到的结果容易使舵面饱和。舵面饱和是控制分配中一个必须重视的问题,它会导致飞机在飞行中自身状态调节能力变差,舵面输入能量大,还容易导致舵面卡死等,所以必须予以重视。针对伪逆法分配效率低和不动点迭代容易舵面饱和的缺点,本文提出了一种基于Armijo搜索准则和BFGS算法相结合的控制分配策略,在整个转矩可达集内搜索最优舵面组合来提高分配效率。

1 控制分配问题描述

假设飞机机动所需的力矩为v(t)∈Rm,舵面输入为u(t)∈Rn,给定控制输入为u(t)。实际输入与期望控制力矩的映射可以表示为f:Rn→Rm(n>m)。操纵面与期望力矩之间的线性关系可以表示为[4]:

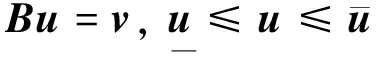
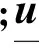
2 基于BFGS算法的控制

针对伪逆法分配效率低下以及不动点迭代法求解二次规划初值敏感和迭代精度问题,本文采用基于Armijo 搜索准则和BFGS 算法相结合的方法进行二次规划问题求解。BFGS算法的基本思想是用迭代点uk处的一阶导数(梯度) 和二阶导数(Hesse阵)对目标函数进行二次函数近似, 然后将二次函数的极小点作为新的迭代点, 并不断重复这一过程, 直至求得满足精度的近似极小点。

设f(u)的Hesse 阵G(u)=2f(u)连续, 截取其在uk处的泰勒展开的前三项得到:

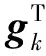
式中，fk=f(uk),gk=f(uk),Gk=2f(uk)。

求二次函数fk(u)的稳定点,得fk(u)=gk+Gk(u-uk)=0,若Gk非奇异,那么解上面的线性方程组(记其解为uk+1) 即得牛顿法的迭代公式

虽然牛顿迭代公式最突出的优点是具有不低于二阶的收敛速度,但是该算法要求目标函数的Hesse阵Gk=2f(uk)在每个迭代点xk处是正定的,否则难以保证牛顿方向dk=-Gk-1gk是f在uk处的下降方向。特别地,当Gk=2f(uk)奇异时, 算法就无法继续进行下去。此外,每一步迭代都需要目标函数的二阶导数, 即Hesee阵, 对于大规模问题,其计算量是惊人的。所以BFGS算法用近似矩阵Bk取代基本牛顿法中的Hesee阵Gk。

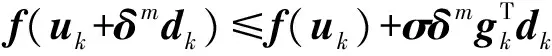
本文采用Armijo搜索最优解,但Armijo搜索一般不能保证矩阵序列{Bk}的对称正定,因此为了保证{Bk}正定,本算法采用的Bk校正公式如下:

式中,yk=gk+1-gk为梯度差;sk=uk+1-uk为位移。

有如下定义:

Sat(u)=

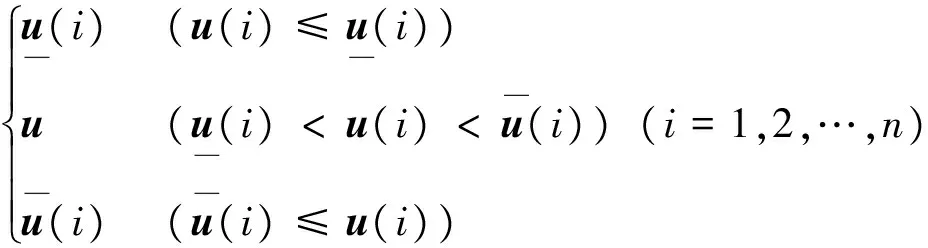
采用Armijo搜索准则和BFGS算法相结合的控制分配算法步骤如下:

Step1:给定参数δ∈[0,1],σ∈[0,0.5], 终止误差0≤ξ≤1,初始对称正定阵B0(通常取为单位阵En)。 令k=0。

Step2:对于迭代初值的选择采用伪逆法求出,初始点u0=B+v必然为控制分配问题的一个可行解,减少了计算量。

Step3:计算gk=f(uk)。若‖gk‖≤ξ, 停止计算, 输出u*≈uk为近似极小点;否则继续下一步。

Step4:解线性方程组得解dk:Gkdk=-gk。

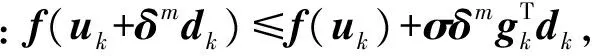
Step6: 由校正公式确定Bk+1。

Step7: 令k=k+1, 转Step3。

3 仿真结果与分析

为了验证上文提出的Armijo搜索准则和BFGS算法相结合的控制分配算法的有效性,采用本方法对某多操纵面飞机的线性化数学模型进行了故障情况下的仿真,飞机模型如下:

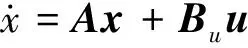
Bu=BvG

式中,状态变量为:x=[ΔV,Δα,Δβ,Δp,Δq,Δr,Δψ,Δθ,Δφ]T,分别为速度、迎角、侧滑角、滚转角速率、俯仰角速率、偏航角速率、偏航角、俯仰角及滚转角增量;控制量为:u=[Δδcl,Δδcr,Δδel,Δδfl,Δδfr,Δδer,Δδr]T,分别为左鸭翼、右鸭翼、左副翼、左后缘襟翼、右后缘襟翼、右副翼、方向舵偏量；虚拟控制量为:v=Gu=[Cl,Cm,Cn]T,虚拟向量由滚转力矩、俯仰力矩、偏航力矩组成,G为舵面的效率矩阵[5]。

在高度为3 000 m,Ma=0.3时,舵面的效率矩阵为:

各个执行器的位置限制如下:

-30°,-30°,-25°]T

为了便于故障诊断和重构,将控制律和分配律分开设计,这样做的优点是如果某一操纵舵面产生故障,那么只需要对故障进行分析,通过调整分配律或者修改控制效率矩阵，而不需要对控制律作出大的修改。多操纵面飞机飞行控制系统的结构如图1所示。

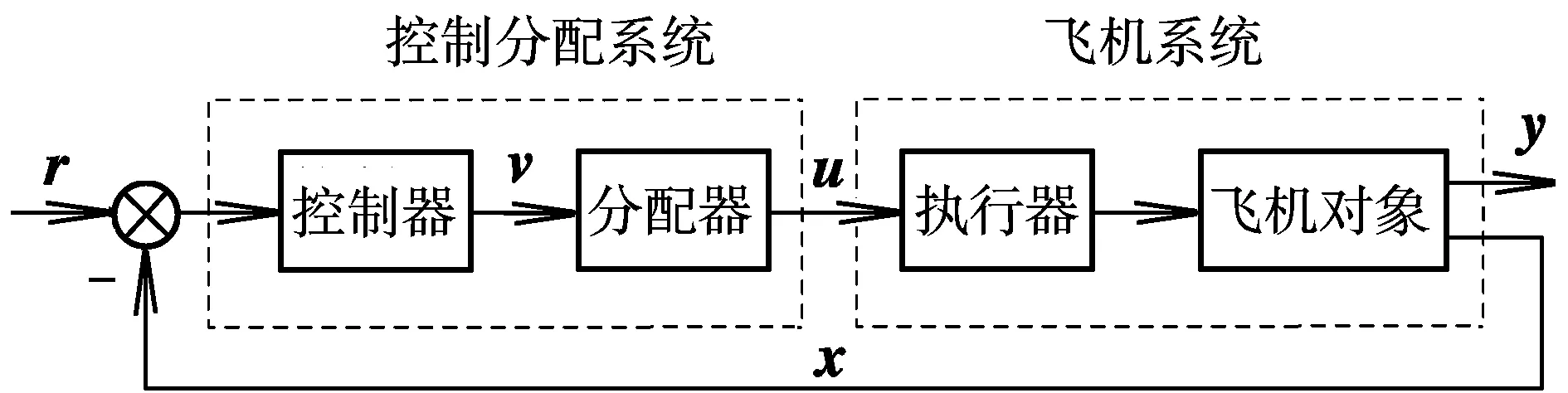
图1 多操纵面飞机飞控系统结构图Fig.1 Flight control system structure of aircraft with multiple effectors

在使用相同的控制律参数和优化函数f(u)=min[(1-λ)(Bu-v)TQ1(Bu-v)+λuQ2u]的前提下,对舵面损伤[6]情况下分别采用不动点迭代法和BFGS算法进行重构仿真。

在左副翼损失70%控制效能的情况下,采用BFGS算法、不动点迭代法重构,姿态角和各个舵面偏转情况如图2～图11所示。

从仿真结果可以看出,在飞机左副翼发生故障的情况下,采用BFGS算法和不动点迭代算法进行控制分配重构时,在指令跟踪曲线过程中俯仰角的过渡时间为1 s,滚转角的过渡时间为1 s,偏航角的过渡时间为0.8 s,都很好地跟踪上了指令,但不动点迭代法的舵面出现了饱和,舵面偏转总和较BFGS算法大,而BFGS通过其他舵面重构跟踪了指令,舵面很少出现饱和;另外，采用不动点迭代法时俯仰角指令跟踪过程中出现较大超调。因此BFGS算法比不动点迭代法解决控制分配问题更有效，采用BFGS分配策略可以提高飞机的重构能力、安全性和机动性能。

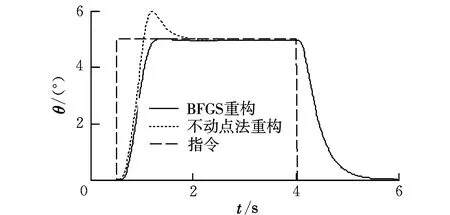
图2 俯仰角曲线Fig.2 Pitching angle curves

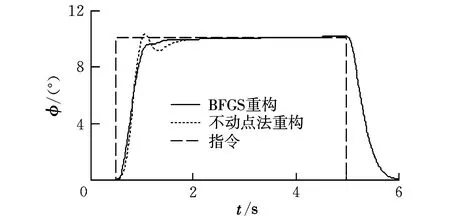
图3 滚转角曲线Fig.3 Rolling angle curves

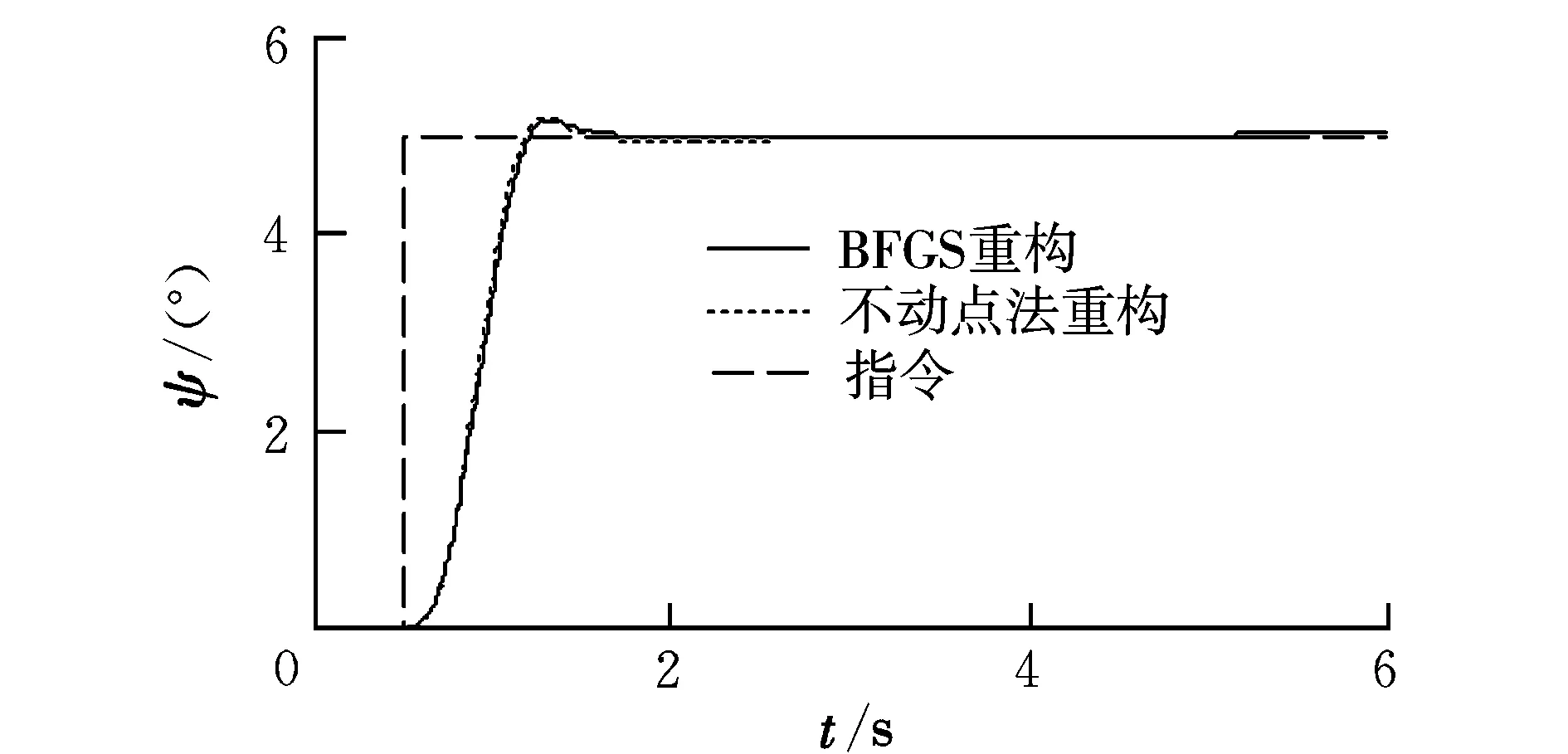
图4 偏航角曲线Fig.4 Yaning angle curves

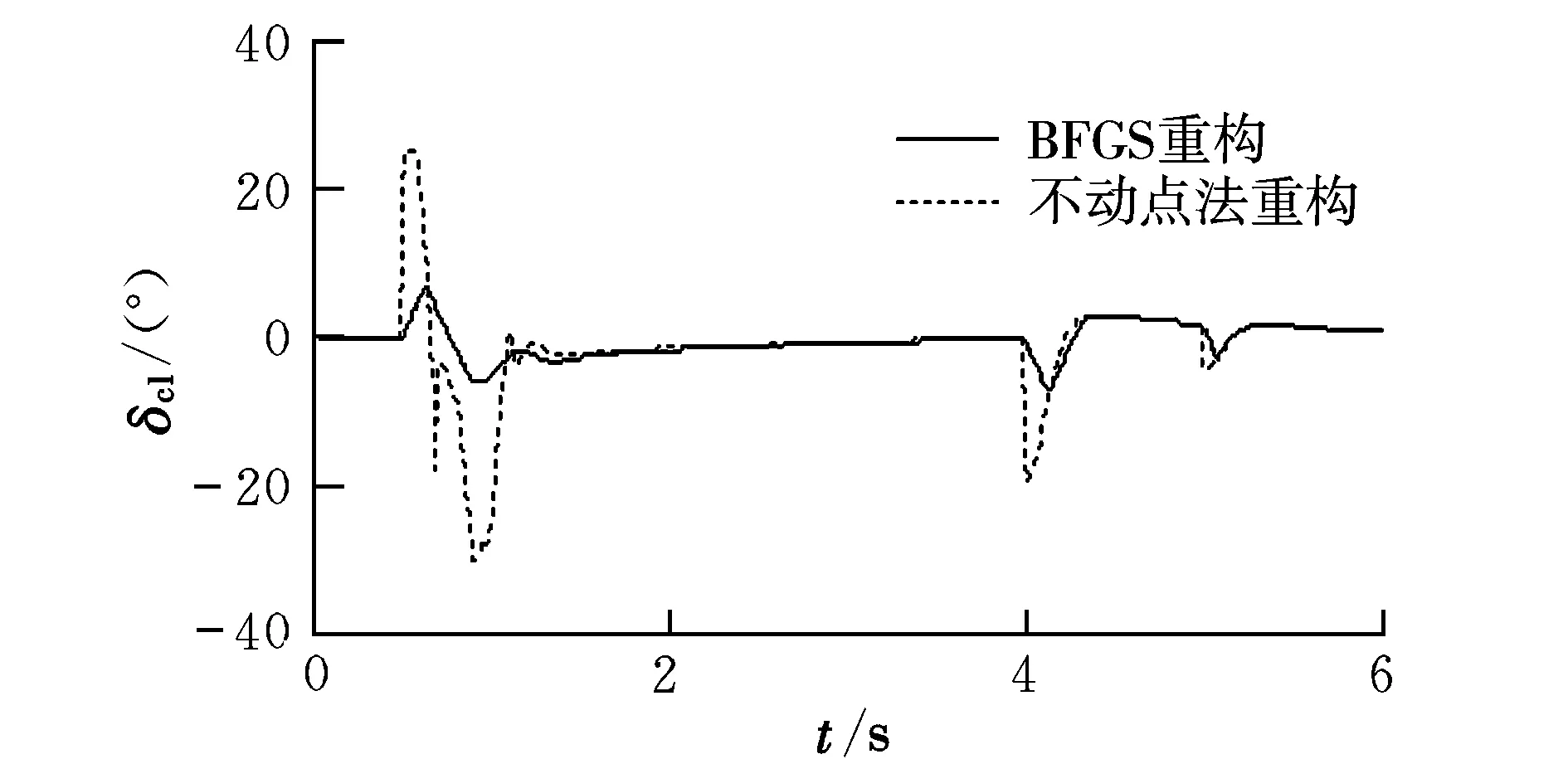
图5 左鸭翼曲线Fig.5 Left canard wing curves

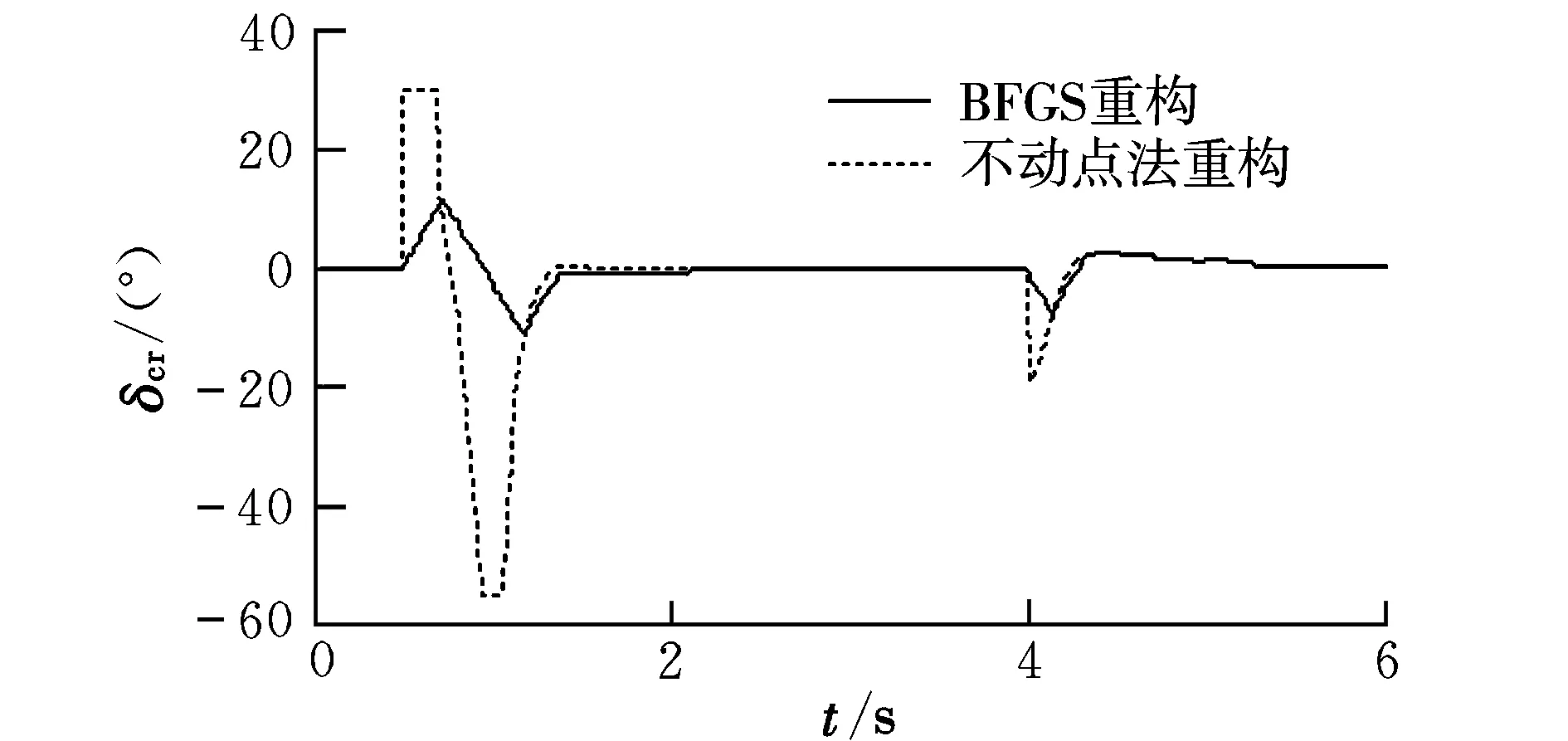
图6 右鸭翼曲线Fig.6 Right canard wing contrast

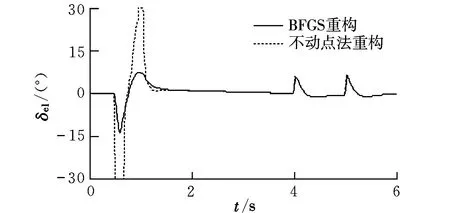
图7 左副翼曲线Fig.7 Left aileron curves

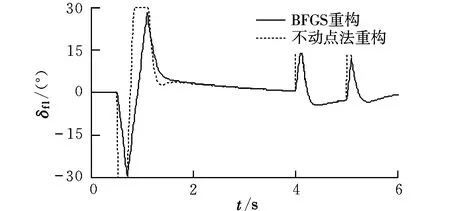
图8 左后缘襟翼曲线Fig.8 Left trailing edge flap curves

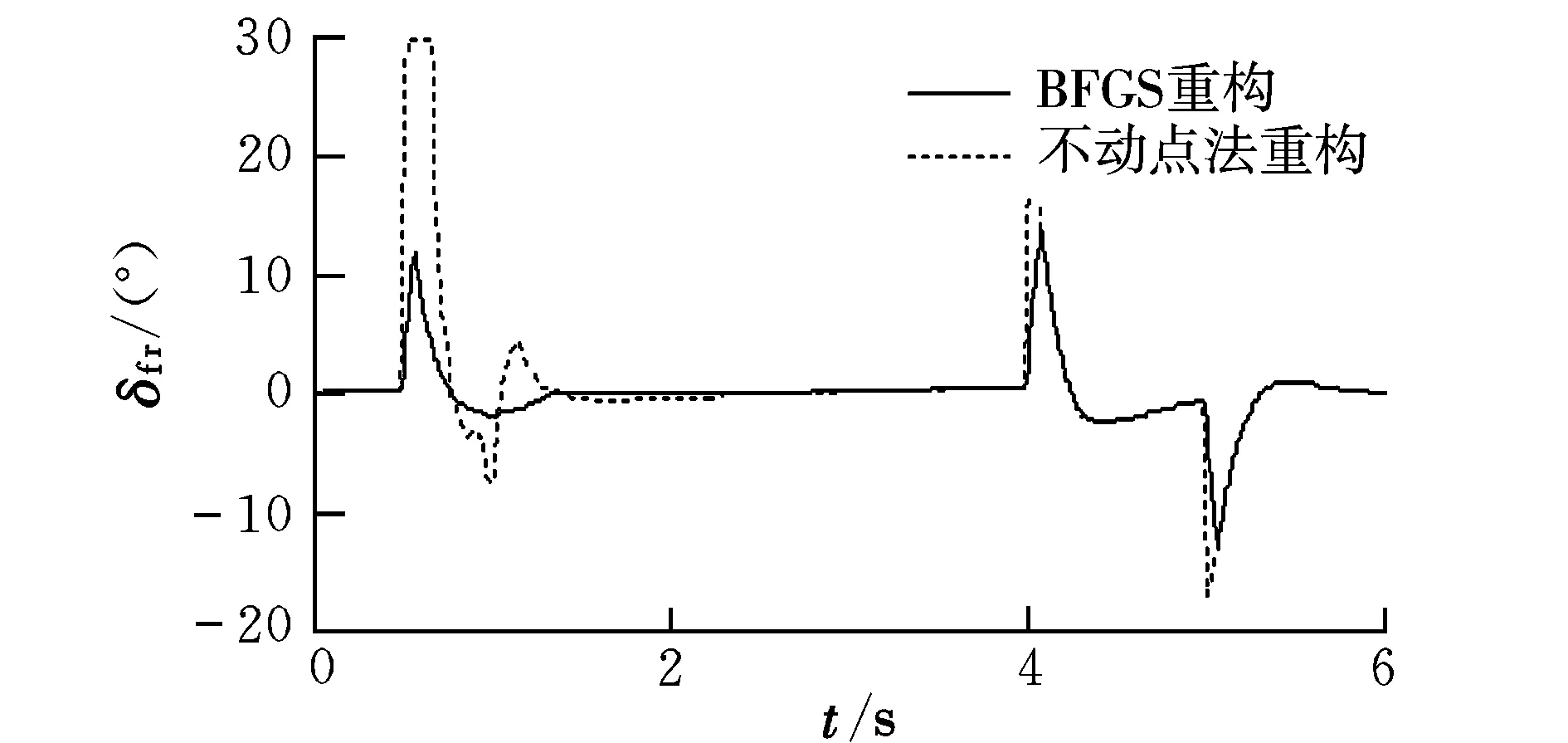
图9 右后缘襟翼曲线Fig.9 Right trailing edge flap curves

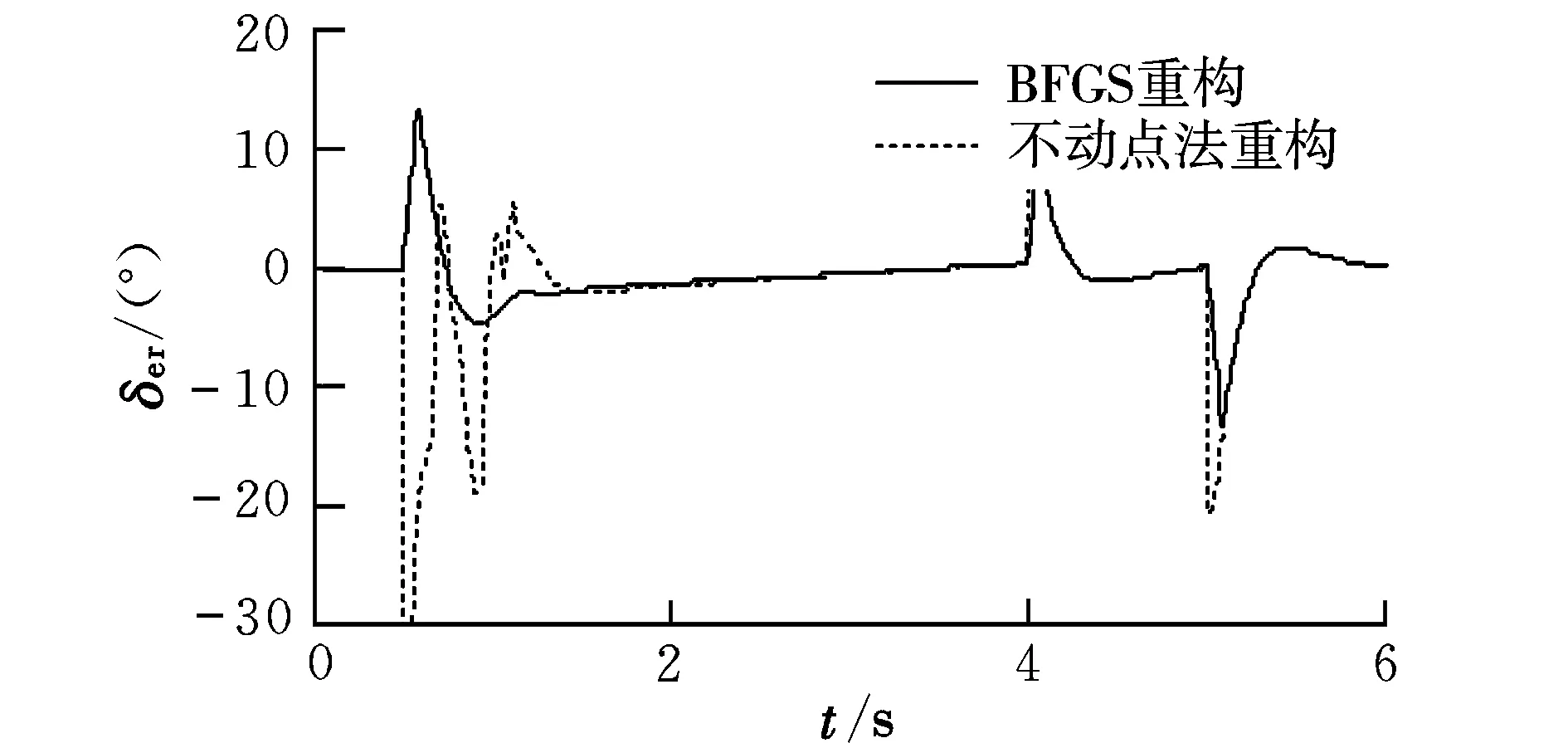
图10 右副翼曲线Fig.10 Right aileron curves

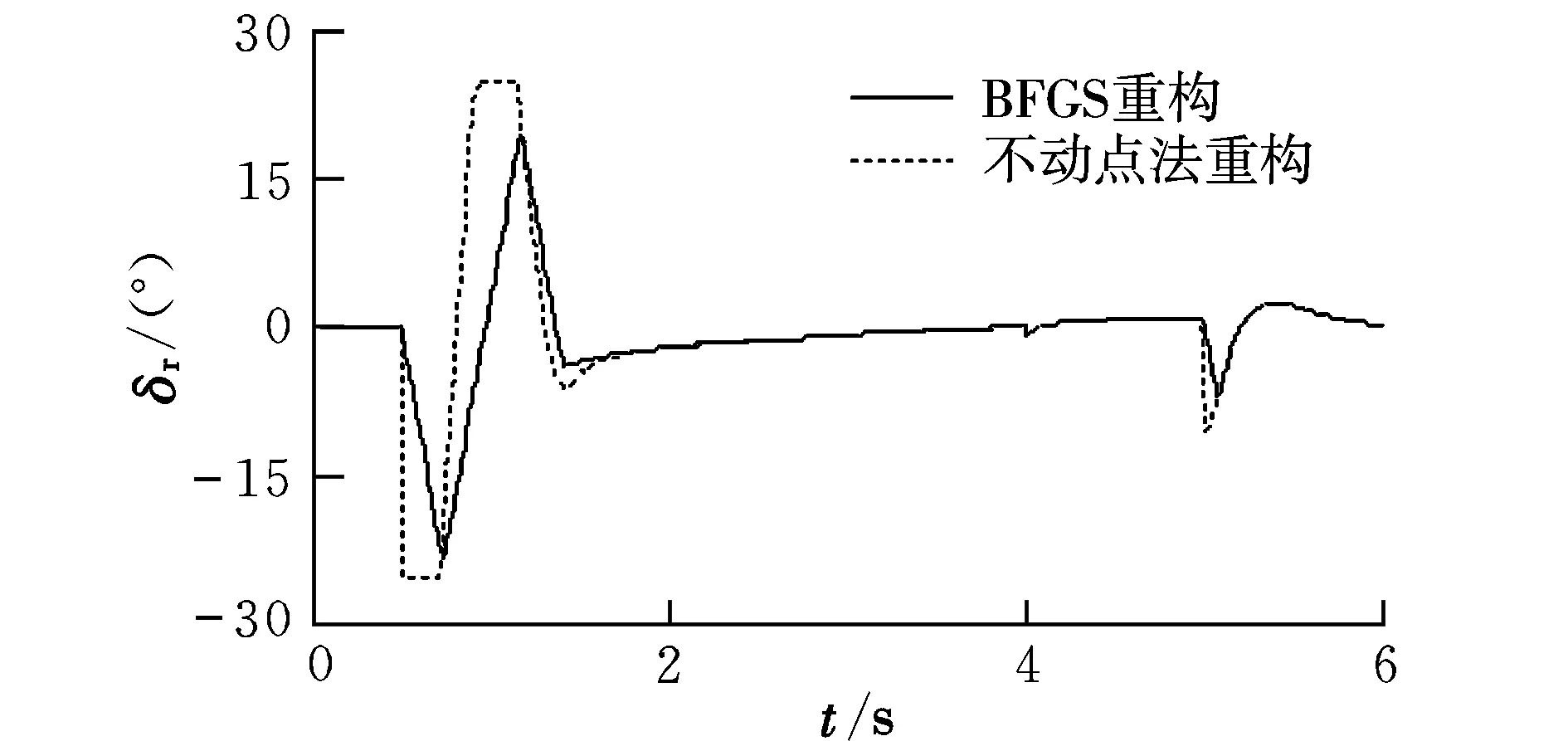
图11 方向舵曲线Fig.11 Rudder curves

4 结束语

本文基于BFGS算法控制分配策略在整个转矩可达集内进行寻优,减少了舵面的饱和。因此BFGS算法能很好地解决控制分配问题,但缺点是Armijo搜索运算时间较长,采用更为有效的搜索策略是本算法的一个改进方向。

[1] 占正勇,刘林.多操纵面先进布局飞机控制分配技术研究[J].飞行力学,2006,24(1):13-16.

[2] 刘建国,葛仁东,夏尊铨,等.非凸函数极小问题的BFGS算法[J].运筹与决策,2004,13(2):62-65.

[3] Jiyeon Kim,Inseok Yang,Dongik Lee.Accommodation of actuator faults using control allocation with modified daisy chaining[C]//Control,Automation and Systems (ICCAS),11th International Conference.Gyeonggi-do,2011:717-720.

[4] 马建军.过驱动系统控制分配理论及其应用[D].长沙:国防科学技术大学,2009.

[5] 史静平.先进飞机多操纵面控制分配方法研究[D].西安:西北工业大学,2009.

[6] 崔玉伟,章卫国,李广文,等.基于线性规划的多操纵面重构控制研究[J].飞行力学,2011,29(2):41-44.

AmethodofquadraticprogrammingcontrolallocationbasedonBFGSalgorithm

ZHANG Ning, ZHANG Wei-guo, LI Guang-wen

(College of Automation, NWPU, Xi’an 710129, China)

This paper presents a method based on Boyden Fletcher Goldfarb Shanno(BFGS)algorithm to solve the control allocation problem of multi-effector aircraft. This control allocation strategy can reduce the saturation of effectors calculated by fixed-point method. In order to demonstrate the feasibility and validity of BFGS control allocation strategy, the control allocation and reconstruction simulation are conducted with a fighter as the research object. The results show that the allocation command can be properly distributed on each surface within the saturation range.

flight control; control allocation; fixed-point method; BFGS algorithm

V249.1

A

1002-0853(2013)06-0508-04

2013-03-21;

2013-06-16; < class="emphasis_bold">网络出版时间

时间:2013-10-22 14:14

航空科学基金资助(20125853035)

张宁(1987-)，男，陕西韩城人，硕士研究生，研究方向为飞行控制和控制分配。

(编辑：姚妙慧)