SF6电弧等离子体输运特性数值分析

，，

(沈阳工业大学电气工程学院，辽宁 沈阳 110870)

SF6电弧等离子体输运特性数值分析

刘晓明，王立森，李争博

(沈阳工业大学电气工程学院，辽宁 沈阳 110870)

为定量描述SF6断路器在大电流开断过程中所产生电弧等离子体参数的动态变化，采用Eindhoven微观电弧模型，得到不同条件下电弧特性参数——电导率和热导率的分布；定量描述了温度、压力与粒子碰撞方式对输运特性的影响。基于热力学平衡模型以及Boltzmann方程数值求解与分析，找到电弧等离子体中输运特性的定量描述，为数值模拟SF6电弧等离子体参数变化分布以及能量逸散提供参数。

SF6断路器，输运特性，电导率，热导率，粒子碰撞

1 引言

SF6断路器在大电流开断过程中所产生的电弧，从微观角度分析整个燃弧历史，是伴随有大量的电离与消电离、扩散与复合的复杂过程。而电弧动态演变受到触头电极材料组成、灭弧介质、断口区域元件物性参数变化、电磁特性变化以及吹弧能量输运通道及气流行为调控的综合影响，且直接影响吹弧气流宏观参数(如，气流压力、温度、速度、密度以及马赫数等)在开断时间(ms)内与极间距(mm)多物理耦合场域内的动态变化。与此同时，电弧等离子体中各组分的无规则运动以及粒子间的碰撞行为对电弧的微观过程发展以及宏观行为表征具有重要影响，涉及粒子数密度、灭弧断口温度以及粒子碰撞方式等诸多因素。其中，电导率、热导率作为表征燃弧过程中的电弧的主要特性参数，在断路器开断过程中动态变化。对于电弧输运特性的研究，文献[1]以粒子组成为基础，对输运特性的计算方法进行了研究；文献[2]对平衡态空气电弧等离子体输运参数进行了微观研究。

基于上述分析，本文在前期工作基础上[3]，基于微观电弧模型，采用Chapman-Enskog方法求解Boltzmann方程，对Botlzmann积分-微分方程进行级数分解，得到电弧电导率、电弧热导率的定量描述；通过粒子间碰撞积分，定量求得电弧等离子体的电导率和热导率。

2 微观电弧模型

常用电弧等离子体微观粒子分析模型有Potapov模型[4]、Eindhoven模型[5]、基于化学反应动力学模型[6]以及基于最小吉布斯自由焓原理模型[7]，不同模型有其各自应用特点。本文采用Eindhoven 模型，该模型具有原理清晰、计算工作量小，并且适于多温度等离子体参数计算，其主要理论依据是质量作用定律、道尔顿分压定律、电荷准中性条件、化学计量平衡条件。

质量作用定律：主要包括电离方程和解离方程。据电离平衡：az+↔a(z+1)++e，得到电离方程。平衡态等离子体中各粒子电离方程：

(1)

其中，ne、naz+、naz+1+分别表示电子az+、重粒子az+、重粒子a(z+1)+的粒子数密度；zaz+、za(z+1)+分别表示粒子az+、粒子a(z+1)+的配分函数；k为玻耳兹曼常数，h为普朗克常量，表示等离子体温度，me表示电子质量；Ei表示粒子az+的电离能，ΔEi表示等离子体内部的电离能降落。

在非平衡态等离子体系统中，电子和重粒子具有不同温度，此时的配分函数是电子温度和重粒子温度的函数。非平衡态状态下，等离子体各粒子数密度电离方程：

(2)

平衡态等离子体中各粒子解离方程：

(3)

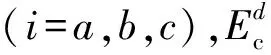
双温情况时，等离子体中电子温度与重粒子温度不同，解离反应或者合成反应主要是重粒子相互碰撞。此时，非平衡态等离子体解离方程可用Guldberg-Wagge方程描述[8]：

(4)

电荷准中性方程：等离子体含有足够数量的正离子和电子，等离子体是宏观呈电中性的电离气体，对外界不显电性，等离子体中正、负离子所带电荷总数相等，表示为：

(5)

化学计量平衡：基于质量守恒，发生解离反应和电离反应前后，各元素化学计量数即摩尔数固定不变，各元素比值为一常量，即：

(6)

其中，ns为与第s种元素有关的j种成分的粒子数密度，np为与第p种元素有关的第m种成分的粒子数密度，C为常数。

气体分压定律：假设气体组分间不发生化学反应，则某一气体在混合物中所占的分压比与该气体在相同条件下单独在整个环境中产生的压力相等，而且所有气体混合物的总压力与各气体组分所占的分压比之和相等。

道尔顿分压定律描述理想气体特性，同样也适用于电离气体。道尔顿分压定律可表示为：

(7)

其中，Te为电子e的温度，Th为重粒子温度，pi是组元i的分压力。当Te=Th=T时为平衡态，Te≠Th时为双温情况。

3 电弧输运特性计算与分析

3.1碰撞积分

电离可由原子吸收光子产生，也可由粒子间的碰撞产生。电子碰撞中性粒子时所需的电离能较少，发生的几率较大。原子-原子相碰撞或者原子-离子相碰撞也可能产生电离，但所需电离能量极大，一般较少发生。

粒子i与粒子j之间的碰撞积分一般定义为[9]：

(8)

(9)

其中，σ(g,θ)为碰撞积分截面积。

相对速度g的定义为：

(10)

体系的简化质量μ定义为：

μ=(m1m2)/(m1+m2)

(11)

在两种组分粒子之间的相互作用势给定的情况下，可求解碰撞积分，进而求解相关输运特性。

电弧等离子体中主要微粒包括电子、原子、中性粒子以及带电粒子(离子)。在等离子体条件下，电子与重粒子之间的碰撞对重粒子组分的分布函数只有微小影响，可忽略电子-重粒子的碰撞对重粒子组分分布函数的影响，基于此，本文在计算输运参数时考虑电子与不同粒子间碰撞，忽略重粒子间的碰撞对计算的影响。

(1)带电粒子间的相互作用

为表征带电粒子Zi和Zj之间的相互作用势，常选择库仑屏蔽电势[10]表示两者之间的作用：

(12)

将库仑屏蔽电势代入式(9)对碰撞积分进行求解。

(2)电子与原子的相互作用

动量截面传输截面积可用于计算电子与原子间的碰撞积分。利用汤姆逊散射截面，可计算电子-原子间的碰撞积分[11]。

汤姆逊散射截面的一般计算公式为：

(13)

其中，W为电子能量；Uiz为电离能(W>Uiz时，即发生碰撞电离)。

3.2输运特性的计算与分析

电弧等离子体的输运参数与粒子质量、动量和能量的传输有关，其能量传输由分子的随机运动和碰撞完成，可采用Boltzmann方程来描述，但该方程复杂，求解困难。本文采用Chapman-Enskog展开法求解Boltzmann方程以得到输运参数。

假定：各粒子速度分布函数满足Maxwell速度分布函数。将Boltzmann方程组进行线性化近似处理，通过利用Sonine多项式进行级数求解，得到相关输运特性参数。

(1)电导率的计算与分析

在热力学平衡条件下，计算电弧等离子体电导率σ(T,P)，由Sonine三阶多项展开式得到[12]。

(14)

在平衡态系统中，宏观系统处于动态平衡状态，不发生宏观变化。在非热力学平衡时，计算电导率σ(T,P)，由Chapman-Enskog方法的四阶多项表达式得到。

(15)

其中，e为电子基本电荷量；ne为电子数密度；me为电子质量；T为温度；qnk可由粒子平均碰撞分Ω(l,s)得到。

(2)热导率的计算与分析

热导率表征材料直接传导热量的能力。电弧热导率主要由平动热传导，反应热传导率和内部热传导三个部分组成，其中平动热传导率包括重粒子热导率和电子热导率。

重粒子平动热导率的表达式可由Sonine二阶近似展开式得到：

(16)

电子平动热导率的表达式也由Sonine二阶近似展开式得到：

(17)

在总压力一定、忽略温度梯度和外部作用力的情况下，可求得各个化学反应的热导率。

4 计算结果与分析

本文以SF6断路器开断过程中所产生的混合金属蒸气电弧为研究对象，计算时假设所有物质均为气态，并且忽略灭弧室中微量杂质气体。燃弧过程中考虑16种主要成分：SF6，SF5，SF4，SF3，SF2，SF，S，F，S2，F2，S+，F+，F-，e，SSF2，FSSF，SF6，此外还考虑Cu，Cu+，Cu2+等金属粒子。

考虑断路器开断过程中金属蒸气的存在，假定开断过程中，金属蒸气浓度为1%、0.5%情况下，对等离子体电导率、热导率进行相关计算。

在平衡态时，金属蒸气浓度非别为1%和0.5%时不同压力条件下触头开断过程中电弧电导率随温度变化的仿真结果，如图1与图2所示。

图1 平衡态含1%Cu电弧电导率随温度压力变化

图2 平衡态含0.5%Cu电弧电导率随温度压力变化

非平衡态时θ=3，金属蒸气浓度非别为1%和0.5%时不同压力条件下触头开断产生的电弧电导率随温度变化的仿真结果，如图3与图4所示。

图3 非平衡态1%Cu电弧电导率随温度压力变化(θ=3)

图4 非平衡态0.5%Cu电弧电导率随温度压力变化(θ=3)

非平衡态，压力P=101325Pa下，不同θ值时电导率随温度变化的仿真结果，如图5所示。

图5 非平衡态电导率随温度变化曲线(P=101325Pa)

由图1～图5可知，平衡态下压力的增加使电导率增大，且温度越高增加率越高，这是由于气压升高的同时增加了相同温度下的电子数密度，体系的电导率变大。在非平衡态下，电导率的变化趋势与平衡态相同，且θ值增大电导率增加，这是因为θ越高电子的数密度越大，体系电导率变大。

平衡态不同金属浓度在相同条件下电导率的变化规律如图6所示。从图中可以看出，金属浓度的增加使得电导率在一定温度范围内增大。

图6 不同浓度金属蒸气电弧电导率随温度压力变化

在平衡态时，金属蒸气浓度非别为1%和0.5%时不同压力条件下触头开断产生的电弧热导率随温度变化的仿真结果，如图7与图8所示。

非平衡态θ=3时，金属蒸气浓度非别为1%和0.5%时不同压力条件下触头开断产生的电弧热导率随温度变化的仿真结果，如图9与图10所示。

由图7～图10可知，平衡态下热导率出现多个峰值，产生的原因是SF6、SF4等粒子的解离作用。压力的增加抑制了解离、电离等化学反应的进行，热导率峰值降低，且峰值相应的推迟到较高温度时出现。非平衡态热导率的变化规律与平衡态相同。

图7 平衡态含1%Cu电弧热导率随温度压力变化

图8 平衡态含0.5%Cu电弧热导率随温度压力变化

图10 非平衡态0.5%Cu电弧热导率随温度压力变化(θ=3)

压力P=101325pa时，不同金属浓度热导率在平衡态与非平衡态下对比如图11所示。由图中可知，金属浓度的变化热导率影响不大；θ增加热导率峰值变小，这是由于θ的增大使得电离反应受到抑制。

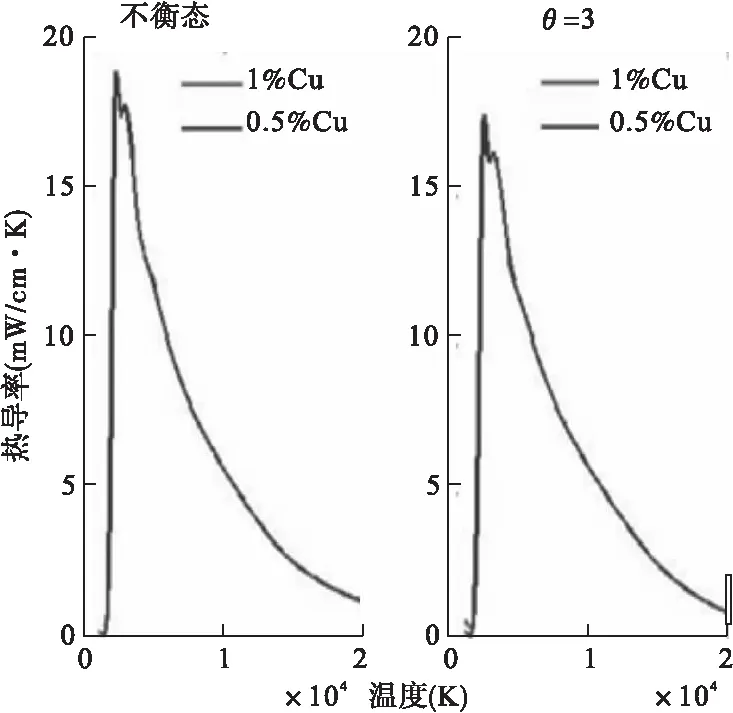
图11 不同条件下电弧热导率随温度压力变化

5 结论

采用数值方法对SF6断路器产生的电弧等离子体进行研究，分析了不同条件下电弧输运特性的分布规律。结果表明：平衡态下随着压力的增加，电导率随温度升高而增加；非平衡态下变化趋势与平衡态时相同，且随着θ的增大，电导率增加。平衡态下电弧热导率出现多个峰值，这主要和SF6、SF4等粒子解离有关。随着气压的升高热导率的峰值相应的被推迟到温度较高的区域才出现，并且峰值变小。非平衡态时热导率的变化趋势与平衡态相同，且随着θ的增大，热导率降低。

[1]王伟宗，荣命哲，吴翊,等.平衡态与非平衡态等离子体物性参数计算模型研究[J].高压电器，2010，46(7)：41-45.

[2]王伟宗，吴翊，荣命哲,等.局域热力学平衡态空气电弧等离子体输运参数计算研究[J].物理学报，2012，61(10).

[3]李争博.开关电弧等离子体输运特性的计算[D].沈阳工业大学，2012.

[4]Gleizes A,Chervy B,Gonzalez J J.Calculation of a two-temperature plasma composition bases and Application to SF6[J].Physics:Applied Physics,1999 (32):2060-2067.

[5]臧春燕，何俊佳，程礼椿.平衡态与非平衡态等离子体的微观模型研究[J].高压电器，2005，41(6)：416-419.

[6]Richley E,Tuma D T.On the Detemination of Particle Concentrations in Multitemperature Plasmas[J].Applied Physics,1982,53(2):8537-854 2.

[7]Aubreton J,Elchinger M F,Fauchais P.New method to calculate thermodynamic and transport propertics of a multitemperature plasma:application to N2 plasma[J].Plasma Chemical & Plasma Processing,1998,18(1):1-27.

[8]Van Z F,Storey S H.The Computation of Chemical Equilibria[M].London:Cambridge University Press London，1970.

[9]谭维翰.一般情况下的碰撞积分修正[J].核聚变与等离子体物理，1985，5(2).

[10]Aubreton,Elchinger M F,Fauchais P.“New Method to Calculate Thermodynamic and Transport Properties of a Multi-Temperature Plasma:Application to N2Plasma,” Plasma Chemistry and Plasma Processing1998,8(1):1-27.

[11]Xiaoming Liu,Zhengbo Li,Yundong Cao,et al.Research on transport properties of the metal vapor vacuum arc.International conference on electric power equipment-switching technology,Xi′an,2011:94-97.

[12]H.Abdelhakim,J P Dinguirard，and S Vacquie,“The influence of copper vapour on the transport coefficients in a nitrogen arc plasma,” J.Phys.D:Appl.Phys.,1980:1427-1438.

NumericalCalculationonTransportPropertiesofSF6ArcPlasma

LIUXiao-ming,WANGLi-sen,LIZheng-bo

(School of Electrical Engineering,Shenyang University of Technology,Shenyang 110870，China)

To quantitatively describe the dynamic variation of the transport parameters of arc plasmas generated in large current interruption of SF6circuit breakers (CBs),the distribution of arc transport characteristics of the electrical conductivity and the thermal conductivity based on Eindhoven micro arc model has been obtained.The effect on the transport properties with temperature,pressure and the particle collisions mode has been describted quantitively.Based on the thermodynamic equilibrium model and analysis of the numerical solution with Boltzmann equation,the transport properties of arc plasma has been obtained,and the basis of numerical simulation for researching dynamic distribution of SF6arc plasma and energy dissipation has been provided.

SF6CB；transport propertiy；electrical conductivity；thermal conductivity；particle collision

1004-289X(2013)05-0057-06

TM501.3

B

2013-01-28

刘晓明(1968-)，女，辽宁丹东人，教授，博士生导师，研究方向为现代高压电器设计及应用、高电压与绝缘技术、智能电器;

王立森(1986-)，男，吉林扶余人，硕士研究生，研究方向现代高压电器设计及应用。