汽轮发电机轴系扭振模态分析

，，

(西南交通大学电气工程学院,四川 成都 610031)

汽轮发电机轴系扭振模态分析

苏永丽，康积涛，吴小刚

(西南交通大学电气工程学院,四川 成都 610031)

以IEEE次同步谐振(Subsynchronous Resonance，SSR)第一标准测试模型为例，详细介绍了如何预测汽轮发电机轴系扭振模态。利用测试信号法计算系统的电气阻尼，通过模态调整法得到模态机械阻尼，利用复转矩系数法判定轴系扭振模态。最后在加入机械阻尼的测试模型中施加三相短路扰动，对轴系各个质量块扭振转矩的幅频分析验证扭振模态预测的正确性，分析结果显示在计及机械阻尼的情况下，只有与电气谐振频率互补的扭振模态发生SSR。

轴系扭振模态；SSR；电气阻尼转矩系数；机械阻尼转矩系数

1 引言

我国能源分布与地区经济发展情况的逆向分布现状，决定了必须采用大容量、超高压、远距离输电。而远距离输电损耗大，串联补偿技术可以很好的解决这个问题，但是含有串联补偿的线路受到扰动后，电力网络和汽轮发电机组之间可能以系统的一个或多个低于同步频率的自然频率交换数量相当可观的能量，此类现象称为SSR[1]。当发生SSR时，使轴系产生疲劳寿命损耗，严重时会造成轴系断裂，危及到电力系统的安全稳定运行，所以有效预测发生SSR的扭振模态显得尤为重要。

2 SSR中轴系扭转振荡产生的机理

图1为最简单的可能引起轴系扭转振荡的系统。

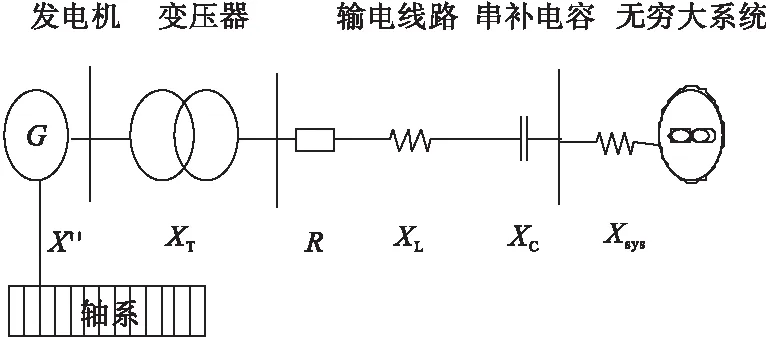
图1 含有串补的输电系统

图中，X″为汽轮发电机的次暂态电抗，XT为变压器的电抗，R、XL为输电线路的电阻和电抗，Xc为输电线路的串补电容，Xsys无穷大系统的电抗。串补电容和线路的电感会产生一个电气谐振频率fer：

(1)

式中：f0为同步频率，X″、XT、XL、Xc、Xsys分别为同步频率下对应的数值。

轴系扭转振荡产生的机理：稳定运行的电力系统受到扰动后，汽轮发电机转子轴系的各刚性质量块间将在一个或多个轴系自然扭振频率fm下产生相互振荡，该振荡将在定子中感应出与轴系自然扭振频率fm互补的电压分量，若电压分量的频率与电气谐振频率fer接近时，由于谐振，该电压分量将在定子回路中产生频率为fer的电流分量，且这个电流分量与电压分量相位相同，该电流分量产生一个与扰动同相位的驱动轴系振荡的扭矩，当该扭矩大于或等于转子的固有机械阻尼转矩时，它就会加剧轴系的扭振振荡，机电相互耦合，此时就发生了轴系扭转振荡[2]。

3 电气阻尼转矩系数计算

3.1 IEEE第一标准模型

用于SSR研究的IEEE第一标准测试模型以内华达工程的发电机组和输电系统为原型[2]。适当调整线路的LC即串补度K(K=Xc/XL)可以产生与内华达工程中出现的SSR问题相似的轴系扭转振荡现象。结构如图2所示。

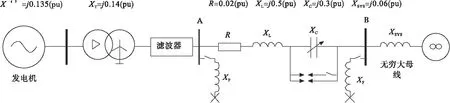
图2 用于SSR研究的IEEE第一标准模型

其中，汽轮发电机的额定容量为892.4MVA，功率因数为0.9，额定电压539kV，额定频率60Hz，取额定容量和额定电压为基准值，对电路中参数进行标幺化，各参数的标幺值如图2。

3.2测试信号法计算电气阻尼转矩系数

测试信号法计算系统的电气阻尼，具体实现步骤参见文献[3],在PSCAD/EMTDC中建立SSR第一测试模型，在MATLAB中进行Fourier分解，得到系统的电气阻尼转矩系数曲线如图3所示。

图3 电气阻尼曲线

由后文4.2多质块轴系模式解耦可知汽轮发电机轴系的模态扭振频率为15.7Hz,20.21Hz,25.55Hz,32.28Hz，47.46Hz。

本文以第三扭振模态为例进行分析，选择串补度为60%，电气谐振频率fer=35.965Hz，此时与轴系的第三个模态扭振频率25.55Hz近似为互补频率。轴系各个模态扭振频率处的电气阻尼转矩系数如表1所示。

表1 模态扭振频率处电气阻尼

4 机械阻尼转矩系数计算

4.1多质块轴系模型

在IEEE第一标准测试模型中，汽轮发电机转子采用分段集中质量弹簧模型，将轴系分为高压缸HP、中压缸IP、低压缸LPA、低压缸LPB、发电机和励磁机六个轴段，各轴段分别视为一个刚性质量块，各个质量块间通过无质量的弹簧相连，如图4所示。

作用在各个质块上的转矩包括机械驱动转矩和电磁制动转矩，相邻质块间的扭矩和阻尼转矩，式(2)、(3)为第i(i=1-6)个质块的线性化运动方程[4]。

图4 汽轮发电机轴系结构

Mi为各轴段的惯性时间常数，Δwi为第i个质块的电气角速度偏差，Dii第i个质块的自阻尼系数，Dii+1、Dii-1为相邻质块的互阻尼系数，kii+1、kii-1为相邻质块的刚度系数，Δδi为第i个质块相对于同步旋转参考轴的电气角位移增量。

由式(2)可以看出个质块之间存在耦合关系，为得到轴系的各个自然扭振模态的信息，需要将轴系解耦。

4.2多质块轴系模式解耦

将式(2)简写为如下形式：

(Mp2+Dp+K)Δδ=ΔTm-ΔTe=ΔT

(4)

分析时不计质块的自阻尼和相邻质块间的互阻尼，由于惯性，机械转矩的变化值不考虑，即ΔTm=0，具体参数参见文献[5]。

对[M-1k]求特征根进而得到轴系的自然模态频率为15.71Hz,20.21Hz,25.55Hz，32.28Hz，47.46Hz；对[M-1k]求右特征向量得到使式(4)解耦的转换矩阵Q。

(5)

对式(4)等式的两边同乘以QT。得到轴系解耦的形式为[4]：

(6)

其中，M(m)=QTMQ，K(m)=QTKQ，Δδ=QΔδ(m),ΔTe(m)=QTΔTe。

解耦后得到轴系扭振模态频率处的模态惯性时间常数Mi(m)为5.4s，55.6s，13.84s，7.84s，22576s。

4.3机械模态阻尼系数

实际测得的阻尼一般以对数衰减率δ或衰减因子σ(σ=fδ)表示，但是机械阻尼受负荷变化的影响，轻载时机械阻尼较小，重载时机械阻尼很大，本文选用选取轻载时的机械阻尼。模态机械阻尼与对数衰减率的关系如式(7)：

Dmi(m)=2Mi(m)δi(m)

(7)

计算得机械模态阻尼转矩系数为：

表2 模态频率处机械阻尼转矩系数

文献[7]给出了一种计算各质量块自阻尼的方法，六个质量块具有五个模态阻尼和一个刚体模式，刚体模式的模态阻尼为零，假定第六个模式为刚体模式，各质量块的自阻尼可通过式(8)计算：

(8)

得到转子轴系Hp、IP、LPA、LPB、发电机、励磁机各轴段的自阻尼系数分别为：0.0275pu，0.0051pu，-0.6809pu，-0.019pu，0.6598pu，0.0074pu。

5 轴系扭振稳定性判断

5.1复转矩系数法

复转矩系数法的基本思想是：使转子旋转角位移增量Δδ在轴系自然扭振频率附近做等幅振荡，分别求出机械子系统和电气子系统的转矩对这一振荡的响应[2]。

(9)

机械转矩系数KM(p)和电气转矩系数KE(p)在频率ε处展开。

(10)

式中，p为微分算子。Km(ε)、Ke(ε)分别为机械、电气弹性系数，Dm(ε)、De(ε)分别为机械、电气阻尼系数。

复转矩系数法的判别依据是在轴系的任何自然扭振频率处满足：

(Dm(ε)+De(ε)(Km(ε)+Ke(ε) =0)>0

(11)

则系统是稳定的，否则发生轴系扭振。

由于电气同步转矩系数Ke与机组轴系的机械弹性系数Km相比要小一个数量级以上[6],所以Km(ε)+Ke(ε) =0近似为Km(ε)=0，而Km(ε)=0的频率对应为轴系的自然扭振频率。也就是说只要保证各个自然扭振频率处的电气阻尼转矩系数和机械阻尼转矩系数和大于零就可以保证系统不发生轴系扭振。

5.2轴系扭振判断

根据2、3得到在模态频率处的电气阻尼和机械模态阻尼可知总阻尼如表3，并根据复转矩系数法判断系统发生第三个模态的轴系扭转振荡。

表3 综合阻尼转矩系数

对于单个输电线路，串补度K(K=XC/XL)不同，对应不同的电气谐振频率，发生轴系扭转振荡的模态也就不同。当网络结构复杂，存在多个串补线路时，电气系统包含多个电气谐振频率，可能发生多个模态的轴系扭转振荡。

6 轴系扭振模态验证

将各个质量块的自阻尼加入系统中进行仿真，设置5s时图2的B处发生三相短路故障，得到各轴段质量块间的扭矩如图4，1.5s时发电机开始运行，1.5～5s各质量块间的扭矩是一个固定的值且在弹性范围之内，5s时系统受到短路扰动，各个质量间的扭矩呈现不同程度的发散状态，此时系统发生轴系扭转振荡。

图5 各轴段质量块的扭矩

将各轴段的扭矩进行幅频分析如图5，由图可以看出第三扭振模态频率25.55Hz的扭振分量最大，其余模态分量很小，在稳定扭矩范围之内，验证系统在计及机械阻尼的情况下发生了第三模态的轴系扭转振荡，与复转矩系数法判定的结果一致。

图6 dT幅频谱

6 结论

基于IEEE第一标准测试模型，利用测试信号法得到电气谐振频率为35.965Hz时的电气阻尼转矩系数。通过模态调整法计算轴系模态频率和机械模态阻尼转矩系数，发现电气谐振频率与第三模态频率25.55Hz互补，将各个模态频率处的电气阻尼转矩系数和机械模态阻尼转矩系数相加，得到第三模态25.55Hz处综合阻尼转矩系数小于零，根据复转矩系数法判断系统发生了第三模态的轴系扭转振荡。

最后在加入轴系质量块自阻尼的IEEE第一标准测试模型中，施加三相短路扰动，系统发生轴系扭转振荡，对各质量块的扭矩进行幅频分析，发现25.55Hz处的扭矩分量最大，验证系统发生第三模态的轴系扭转振荡。

含有串补的高压输电系统系统在计及机械阻尼的情况下只有与电气谐振频率互补的扭振模态发生轴系扭振。

[1]钟胜.与超高压输电线路加串补装置有关的系统问题及其解决方案[J].电网技术，2004(28)，6:26-29.

[2]程时杰，曹一家，江全元.电力系统磁同步振荡的理论与方法[M].北京：科学出版社，2009.：79-80，131，191-192.

[3]徐政.交直流电力系统动态行为分析[M].北京：机械工业出版社，2004：166.

[4]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002：295-296.

[5]IEEE Subsynchronous ResonanceWorking Group.First benchmark model for computer simulation ofsubsynchronous resonance[J].IEEE Transactions on Power Apparatus and Systems,1977,96(5):1565-1572.

[6]Kundur P.Power System Stability and Control.First Edition.New York:McGraw-Hill Jnc.,1994.

[7]张帆.电力系统次同步振荡抑制技术研究[D].浙江：浙江大学，2007：128-129.

ShaftTorsionalVibrationModePredictionofTurbineGenerator

SUYong-li,KANGJi-tao,WUXiao-gang

(School of Electrical Engineering of Southwest Jiaotong University,Chengdu 610031)

Based on the IEEE subsynchronous resonance,the thesis taskes the advantage of an example of the first standard test model to depict how to predict torsional vibration mode of steam turbine generator shafting in great details.The electrical damping can be calculated with method of the test signal,the modal mechanical damping can be figured out by means of the modal adjustment,and the complex torque coefficient method determines the shaft torsional vibration mode.In the end,three-phase short perturbation is applied to the test model with the attachment of mechanical damping and mass of shafting torsional vibration torque amplitude and frequency are analyzed to verify the correctness of the torsional vibration mode prediction,then the analysis's outcome showed that when the mechanical damping taken into account,if and only if the torsional vibration mode are complementary to electrical resonance frequency,then SSR of the torsional vibration mode comes into being.

shaft torsion vibration mode;SSR;electrical damping;mechanical damping

1004-289X(2013)05-0066-05

TM77

B

2012-12-11

苏永丽(1984-)女，籍贯河北，硕士研究生，研究方向为电力系统稳定与控制。