边缘节点的自适应半径调整算法

韩春延

(江南大学 物联网工程学院, 江苏 无锡 214122)

边缘节点的自适应半径调整算法

韩春延

(江南大学 物联网工程学院, 江苏 无锡 214122)

降低覆盖冗余度是提高无线传感器网络覆盖度的一种措施．在DCAC(Dynamic adaptive coverage adjusting scheduling)的算法的基础上,给出了边缘节点和局部全约束状态的定义,并且提出了边缘节点的自适应半径调整的算法．与DCAC算法进行比较其仿真结果表明,无线传感器网络的覆盖冗余度相对降低,提高了网络的覆盖度,并且活跃节点的个数相对减少．

覆盖冗余度; 边缘节点; 半径调整; 无线传感器网络

0 引言

无线传感器网络是由部署在监测区域内大量的廉价传感器节点组成的多跳自组织网络系统． 无线传感器网络在许多地方得到广泛的应用, 例如军事、医院监控、工业生产中的安全监控、自然环境的检测等[1-4]． 根据传感器节点是否有移动能力,无线传感器网络覆盖可以分为静态网络覆盖和动态网络覆盖． 静态网络覆盖又分为区域覆盖、点覆盖和栅栏覆盖[5,6]． 区域覆盖研究的是对目标区域的检测问题．Bai等人[7]研究了区域覆盖,提出了计划部署模型,渐近达到最优覆盖,但是需要精确部署节点,因此应用范围相对有限; 点覆盖研究的是对离散目标点的覆盖问题;栅栏覆盖研究的是运动物体穿越部署区域被检测到的概率问题,Kumar等人[8]提出了弱栅栏覆盖的概念,并推导出了其存在和不存在的临界条件, Liu等[9]提出强栅栏覆盖与区域长宽比的直接关系,即随着长宽比的增大,穿越路径的存在可能性趋近为1．

为达到应用要求,无线传感器网络的覆盖需要在保证服务质量的条件下,使得对监测区域的覆盖范围达到最大化．无线传感器节点体积微小,靠能量十分有限的电池工作．由于传感器分布区域较大,而且部署区域的环境复杂,有时人员无法到达更换电池．所以,很多的应用为了保证网络的服务质量要求网络的覆盖度kgt;1．无线传感器网络在大片的监测区域内通常密集部署,而且由于节点的数量较多,一般采用随机播撒的方式．这样就造成有的区域节点过多,出现覆盖冗余的现象,而有的区域则由于节点过少造成覆盖盲区．韩志杰等提出了一种基于区域覆盖的自适应传感器半径调整算法[10]．该算法通过节点自适应选择最佳的覆盖半径,消除覆盖盲区,减少覆盖冗余,从而减少节点能量虚耗,提高覆盖效率．但是在k覆盖传感半径调整算法中,如果监测区域较大,节点较多,导致边缘节点增加,由于边缘节点大部分属于非全约束状态,则根据算法可知节点的半径增加到最大半径,从而造成区域边缘覆盖冗余度增大,能耗增加． 因此本文针对边缘节点提出了边缘节点半径调整算法,降低网络的覆盖冗余度．

1 网络模型

1) 假设节点的感知模型为布尔模型[1]．在布尔模型中,节点P的感知半径为R,对于检测区域内的任一点s,节点P感知到点s处事件信息的概率可以用下列公式表示为:

(1)

其中,d(P,s)是节点P到区域内点s的欧式距离．从(1)式中可以看出,当监控对象存在于节点的感知区域内时,节点监测到对象的概率则恒为1;当监控对象不存在于节点的感知区域内,则被监测到的概率恒为0．

2) 假设节点是静止的,可以通过装置GPS确定自身的位置,并且节点可以通过自身的位置信息计算距自己最近的检测边界的距离．

3) 假设所有的传感器节点同构,即具有相同的计算通信能力、初始能力和存储能力．传感器节点都有相同的最大传感半径Rmax,且传感器半径可以根据需要进行调整.

4) 假设监测区域的边界可以通过数学表达式进行描述.

2 算法相关定义和定理

处于监测区域边缘的节点具有共同的特点[10]．一是节点的感知范围有一部分无法在监测区域内;二是节点大部分处于非全约束状态;三是节点到监测边界的垂直距离绝对不会大于感知半径．根据文献[10]中边缘节点的特点给出边缘节点的定义．

定义1[10]在一个监测区域内,假设节点P的半径为r,节点P到最近监测区域边界的垂直距离为d,若d≤r,则节点为P边缘节点,如图1所示．

图1 边缘节点P的参考图

图2为边缘节点的几种位置图．图2a中节点P在监测区域的感知范围不能被邻居节点覆盖,且节点在P监测范围内的感知的圆弧上的点被邻居节点全部覆盖． 图2b中节点在P监测区域内的感知范围不能被邻居节点覆盖,且节点P在监测区域内的感知圆的圆弧上的点不能被邻居节点全部覆盖．图2c中节点P在监测区域的感知圆感知范围内的每一个点都能被邻居节点覆盖．

图2 边缘节点P的位置图

根据上述3种情况,基于文献[10]中的约束圆弧和全约束状态的定义对边缘节点感知圆圆弧在监测区域内的约束性和边缘节点在监测区域的约束状态进行定义．

定义2 边缘节点的有效约束圆弧:若一个边缘节点在监测区域内的感知圆部分的某段圆弧被其任何一个邻居节点的感知圆覆盖,则称这段圆弧为有效约束圆弧．

定义3 边缘节点的局部全约束状态: 一个边缘节点在监测区域内的感知圆部分的圆弧全部为有效约束圆弧时的状态为边缘节点的局部全约束状态．

基于文献[10]中普通节点的对覆盖盲区覆盖的定理以及节点在覆盖过程中为全约束状态并不会产生新的盲区的定理的证明可得定理同样适用于边缘节点．定理可以如下表述．

定理1 设边缘传感器节点为P,传感半径为r,节点P的邻居节点和监测边界的覆盖盲区的盲区顶点分别为A1,A2,…,An,若存在maxd(P,Ai)≤r,则必P覆盖盲区,其中d(P,Ai)是边缘节点P和Ai的欧式距离,如图3所示．

图3 节点P在监测区域内的覆盖盲区

定理2 设边缘传感器节点为P,传感半径为r,节点P的邻居节点和监测边界的覆盖盲区的盲区顶点分别为A1,A2,…,An,节点P为局部全约束状态,将节点P的半径从r调整到r′,且r′=maxd(P,Ai),i=1,2,…,n,则节点P在半径调整过程中一直处于局部全约束状态．

定理3 若在监测区域内边缘节点P的感知圆半径由r调整到r′的过程为局部全约束变化过程,则边缘节点P的传感半径由r调整为r′不会产生新的覆盖盲区．

从上述3个定理得知,对于监测区域内的边缘节点在监测区域内的半径调整为全约束变化,并且半径调整后可以覆盖在监测区域内的覆盖盲区,并且半径调整的过程中不产生新的覆盖盲区．本文的算法只是研究在监测区域内的覆盖盲区,在监测区域内的边缘节点的感知圆部分,并不考虑监测区域外的边缘节点感知圆部分．

3 边缘节点的半径调整算法

3.1 算法分析

1) 确定边缘节点．根据定义1中的要求,比较节点P的半径r和节点到监测边界的垂直距离d,若d≤r,则节点P为边缘节点,否则,则不是边缘节点．

2) 判断边缘节点感知圆在监测区域内是否为局部全约束状态．判断在监测区域内的边缘节点的感知圆圆弧能否被节点的μ邻居覆盖,若能覆盖,则为局部全约束状态,否则不是．若边缘节点不是局部全约束状态,则以最大能力覆盖μ邻居的覆盖盲区区域．若边缘节点是局部全约束状态,则求出节点P的所有邻居节点的感知圆在该节点的感知圆内彼此相交的交点以及在该节点感知圆内的邻居节点与监测边界的交点,分别表示为A1,A2,…,An．

3) 若边缘节点为局部全约束状态,但不存在A1,A2,…,An,则可知节点P的感知区域被其邻居节点全部覆盖,则将节点P的感知半径调整为零．若存在A1,A2,…,An,则设其被邻居节点覆盖的次数为β,并且保证达到k覆盖．当β≤k+1时,Ai为盲区顶点;否则为普通圆内交点．

4) 若A1,A2,…,An中不存在盲区顶点,说明边缘节点P的邻居节点能够完全覆盖该节点的感知区域,因此边缘节点P的传感半径调整为零.

5) 若A1,A2,…,An中存在盲区顶点,说明边缘节点P在监测区域内存在覆盖盲区．根据定理1～定理3,则将边缘节点P的半径从r调整到r′,且r′=maxd(P,Ai),i=1,2,…,n,此过程为局部全约束变化,不会产生新的覆盖盲区．

3.2 算法步骤

begin 对每个节点ni

begin 监测区域的函数

if 节点到边界的最短距离d≤r

则节点为边缘节点

调用PtlnRegion函数判断边缘节点是否为局部全约束状态

if 边缘节点为局部全约束状态

if 边缘节点不存在覆盖盲区

r调整为0

else if 边缘节点的覆盖盲区存在盲区定点,r调整为0

else r调整为r′

else 边缘节点为非局部全约束状态,r调整为rmax

end

end

end

end

end

end

4 仿真分析

为了验证边缘节点加入算法后的性能,分别从覆盖冗余度,活跃节点,能力消耗进行了模拟实验,并与自适应半径调整算法进行了比较．

4.1 覆盖冗余度的比较

覆盖冗余度:监测区域内的所有节点覆盖面积之和与区域中所有节点的覆盖范围的并集的比值[1]．可以用下式表示．

(2)

其中,Si表示节点i的感知圆覆盖面积．由覆盖冗余度表达式可以看出,覆盖冗余度越低,节点的感知区域重叠越小,节点的利用率越高．

在200m×200m的区域内,随机撒入800个节点,最大半径为10m,分别用自适应半径调整算法、及在自适应半径调整算法后加入边缘节点算法的进行调度,并计算出各自分别在1次覆盖,2次覆盖和3次覆盖时的覆盖冗余度，并用表1表示. 仿真结果表明,加入边缘节点算法后,监测区域的覆盖冗余度降低,说明加入边缘节点算法后,监测区域的节点利用率提高．

表1 不同覆盖次数下的覆盖冗余度比较

4.2 活跃节点个数的比较

活跃节点是指监测区域处于工作状态的节点．对于一定的监测区域,在保证网络覆盖要求的前提下,活跃节点的个数越少,休眠的节点越多,节约的网络能量更多,网络的生存时间越长．在200m×200m的区域内,节点的最大感知半径为20m,随机部署的节点个数分别取(900,1000,1100,1200,1300,1400,1500)．仿真对不同的部署参数分别进行了10次实验,然后取其平均值作为最后的结果．在自适应半径调整算法,及在自适应半径算法结果后加入边缘节点算法调度后的活跃节点个数比较仿真结果如图4所示．由图4的活跃节点比较可知,自适应半径调整算法的结果后加入边缘节点算法后的调度结果显示活跃节点个数减少,说明改进后的算法调度后,网络的性能更好．

4.3 能量消耗的比较

传感器节点体积微小,只能携带能力有限的电池．由于传感器节点个数多,而且部署区域的环境复杂,有些区域人员不能到达,所以传感器节点更换电池的方式来补充电源很难实现．如何减少传感器节点的能力消耗是传感器网络面临的重大挑战．

传感器半径调整会消耗计算能量,发送和接受数据消耗能量．由于计算能量消耗较少,因此可以忽略不计．传感器节点的感知模块的能量消耗可以表示为E=ur2,u为消耗系数,为常量．

覆盖区域的平均能耗[11,12]为

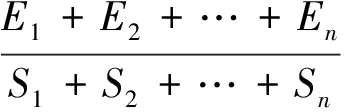
(3)

其中Ei为节点i的感知能量消耗,Si为节点i的感知圆覆盖面积,ri为节点i的感知半径．

在150m×150m区域内分别部署的节点个数(800,1000,1200,1400,1600,1800,2000)．节点的最大感知半径为10m,在自适应半径调整算法,自适应半径调整算法结果再运用边缘节点算法调度后的覆盖区域的平均能耗比较如图5所示．

图4 活跃节点个数的比较

图5 平均能耗的对比

从图5的结果中可以看出,加入边缘节点算法后,覆盖区域的平均能耗减少,延长了节点的使用时间,从而延长了无线传感器网络的生存时间,提高了网络性能．

5 总结

本文提出了边缘节点的半径调整算法,并将算法加入DACA算法的应用中．该算法对监测区域的边缘节点进行了研究,改变了边缘节点在非全约束状态下半径调节到最大半径的情况,让边缘节点针对自身的覆盖盲区的情况进行半径调整,尽可能的降低网络的覆盖冗余度．为了验证DACA算法加入边缘节点半径调整算法后的性能,主要从覆盖冗余度,活跃节点个数和平均能量消耗三个方面进行了模拟仿真实验和分析．实验结果表明,边缘节点半径调整算法和DACA算法结合后,调度后的结果表明,网络的覆盖冗余度降低,减少了活跃节点的个数和节点能耗,提高了网络的覆盖率,延长了网络的生存时间,从而提高了网络的覆盖性能．由于边缘节点半径调整算法需要知道监测区域的数学表达,因此只能应用与一些较简单的监测区域．

[1] 孙利民, 李建中, 陈渝. 无线传感器网络[M]. 北京: 清华大学出版社, 2005.

[2] 马祖长, 孙怡宁, 梅涛. 无线传感器网L络综述[J]. 通信学报, 2004, 25(4):114-124.

[3] 王汝传, 孙丽娟, 黄海平,等. 无线传感器网络技术及其应用[M]. 人民邮电出版社. 2011.

[4] David E C, Wei H, Wireless sensor networks[J]. Communications of ACM, 2004, 47(6): 30-33.

[5] Bonnet P, Gehrke J, Seshadri P. Querying the physical world[J]. IEEE Personal Communication, 2007, 7(5): 10-15.

[6] Akyildiz I F, Su W, Sankarasubramaniam Y. Wireless sensor Networks: a Survey[J]. Computer Networks,2002,38(4):393-422.

[7] Bai X L, Kumars, Xuan D, et al. Deploying wireless sensors to achieve both coverage and connectivity[M].//Proc of the 7th ACM International Symposium on Mobile Ad hoc Networking and Computing. New York: Association for Computing Machinery, 2006: 131-142.

[8] Kumars, Laith, Arora A. Barrier coverage with wireless sensors[M].//Proc of the 11th Annual International Conference on Mobile Computing and Networking. New York: Association for Computing Machinery, 2005: 284-298.

[9] Liu B Y, Dousseo, Wang J. et al. Strong barrier coverage of wireless sensor networks[M].//Proc of the 9th ACM International Symposium on Mobile Ad hoc Netwoking and Computing. New York: Association for Computing Machinery, 2008: 411-420.

[10] 韩志杰, 吴志斌, 王汝传, 等. 新的无线传感器网络覆盖控制算法[J]. 通信学报, 2011, 32(10): 174-184.

[11] Woehrlem, Brockhoffd, Hohmt, et al. Investigating Coverage and Connectivety Trade Offs in Wireless Sensor Netwoks: the Benefits of MOEAS, TIK Report 294[R]. Zurich: Computer Engineering and Networks Lab, ETH Zurich, 2008.

[12] Hefeedam, Bagherim. Efficient K-Coverage Algorithms for Wireless Sensor Networks[D]. Vancouver: Simon Fraser University, 2006.

AdaptiveRadiusAdjustmentAlgorithmforEdgeNodes

HAN Chun-yan

(School of IoT Engineering, Jiangnan University, Wuxi Jiangsu 214122, China)

The lower coverage redundancy is a kind of measures to improve the wireless sensor network coverage. In this paper, the edge nodes and local full constraint condition are defined.At the same time, this paper put forward the edge nodes adaptive radius adjustment algorithm based on the algorithm of DACA(Dynamic adaptive coverage adjusting scheduling).Finally, the algorithm of DACA joins in the algorithm of this paper and then compared with the DACA algorithm.The simulation results show that coverage redundancy of the wireless sensor network relatively lower, the network coverage improved and the number of active nodes relatively less.

coverage redundancy; edge nodes; radius adjustment; wireless sensor network

2013-03-15

韩春延(1988-), 女, 山东聊城人, 硕士研究生, 研究方向为无线传感器网络覆盖控制．

TP393

A

1671-6876(2013)02-0129-06

[责任编辑蒋海龙]