向量优化问题拟有效解的最优性充分条件*

廖 伟，彭 婕

(重庆师范大学数学学院，重庆401331)

近年来，向量优化理论与应用研究越来越受到广大学者的关注和重视。有效解是向量优化问题中的一个重要概念，关于有效解的研究也取得了一些成果，见文献［1-3］。随着研究的进一步发展，向量优化问题的近似解的概念被提出来。其中，拟有效解是向量优化近似解的一个重要的概念。Guptia等人在文献［4］中利用近似凸函数，给出了非光滑向量优化问题的拟有效解的最优性条件。Bhatia等人在文献［5］中提出了几类新的广义近似凸函数的概念并举例验证了这几类广义近似凸函数的存在性，同时建立了向量优化问题的拟有效解的充分最优性条件。在文献［4-5］的基础上，利用距离函数给出了四类新的广义近似凸函数的概念并建立了向量优化问题的局部拟有效解和局部有效解的充分最优性条件。

1 预备知识

设Γ是实拓扑向量空间，Rp是P维欧几里得空间是Rp的非负序锥。对任意x，y∈Rp，定义下面的序关系:

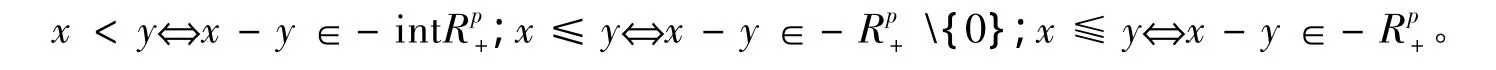
考虑下面的向量优化问题:

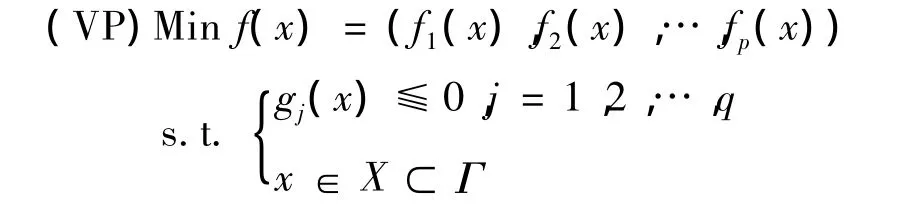
其中 f:X→Rp，g:X→Rq。令 S={x∈X:gj≦0，j=1，2，…，q}是 VP 的可行集。

定义1 称x0∈S是VP的有效解，如果对任意x∈S，f(x)－f(x0)∉－{0}。

定义2 称x0∈S是VP局部有效解，如果存在x0的邻域U，使得对任意x∈S∩U，f(x)－f(x0)∉－{0}。

定义3 称x0∈S是VP的拟有效解，如果存在，对任意x∈S，f(x)－f(x0)+αd(x，x0)∉－{0}。

定义4 称x0∈S是VP的局部拟有效解，如果存在α∈int，存在x0的邻域U，使得对任意x∈S∩U，f(x)－f(x0)+αd(x，x0)∉ －{0}。

定义5［6］称函数ψ:X→R在x∈X是局部Lipschitz的，如果存在正常数L和x的邻域U，使得对任意00x1，x2∈U，d(ψ(x1)，ψ(x2))≤Ld(x1，x2)。

定义6［6］令ψ:X→R在x∈X是局部Lipschitz的，则ψ在x沿方向v∈Γ的Clarke广义方向导数为00

定义7［6］函数 ψ 在 x∈X 的 Clarke次微分，记为∂ψ(x)，定义为∂ψ(x)={ξ∈Γ*:ψ0(x;v)≥［ξ，0000v］，∀v∈Γ}。

下面给出VP的拟有效解的一个必要最优性条件。

定理1 设x0∈S是VP的拟有效解，令g(x)在x0处满足一定的约束规格或者正则性条件。进一步地，设 fi，i=1，2，……，p 和 gj，j=1，2，……，q 在 x0是局部 Lipschitz的，则存在 α∈int()，λ∈和 u∈使得:

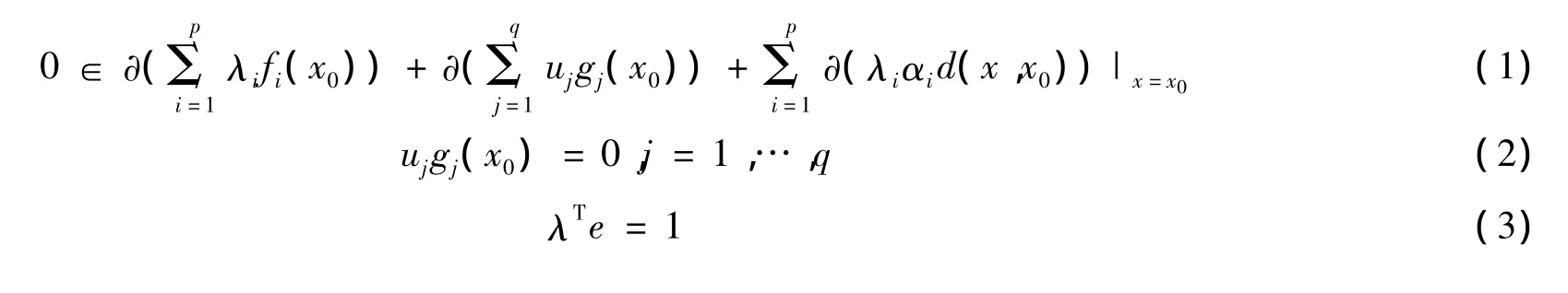
2 四类新的广义近似凸性

首先，回顾一下Lipschitz函数的伪凸性和拟凸性的定义。一个Lipschitz函数ψ:X→R称为在x0∈X是伪凸，如果对任意 x∈X，［ξ，x－x0］≧0，对某些 ξ∈∂ψ(x0)⇒ψ(x)≧ψ(x0)。

类似的 ψ 称为在 x0∈X 是拟凸，如果对任意 x∈X，ψ(x)≦ψ(x0)⇒［ξ，x－x0］≦0，∀ξ∈∂ψ(x0)。

定义8 称函数ψ:X→R在x0∈X是Ⅰ型近似伪凸，若对所有c＞0，存在x0的邻域U，使得对某些ξ∈∂ψ(x0)，［ξ，x－x0］≧0，有 ψ(x)－ ψ(x0)≧ －cd(x，x0)，∀x∈U∩X。

定义9 称函数ψ:X→R在x0∈X是Ⅱ型近似伪凸(Ⅱ型严格近似伪凸)，若对所有c＞0，存在x0的邻域 U，使得对某些 ξ∈∂ψ(x0)，［ξ，x－x0］+cd(x，x0)≧0，有 ψ(x)≧(＞)ψ(x0)，∀x∈U∩X。

定理2 若ψ:X→R在x0∈X是Ⅱ型近似伪凸，则ψ在x0是Ⅰ型近似伪凸。

证明 假设对某些 ξ∈∂ψ(x0)，［ξ，x－x0］≧0，则对任意 c＞0 有［ξ，x－x0］+cd(x，x0)≧0。

由ψ是Ⅱ型近似伪凸，则存在x0的邻域U，使得对任意x∈U∩X，ψ(x)≧ψ(x0)。故有ψ(x)≧ψ(x0)－cd(x，x0)。

因此ψ在x0∈X是Ⅰ型近似伪凸。

定义10 称函数ψ:X→R在x0∈X是Ⅰ型近似拟凸，若对所有c＞0，存在x0的邻域U，使得对任意x∈U∩X，ψ(x)≦ψ(x0)，有［ξ，x－ x0］－cd(x，x0)≦0，∀ξ∈∂ψ(x0)。

定义11 称函数ψ:X→R在x0∈X是Ⅱ型近似拟凸(Ⅱ型严格近似拟凸)，若对所有c＞0，存在x0的邻域 U，使得对任意 x∈U∩X，ψ(x)≦(＜)ψ(x0)+cd(x，x0)，都有［ξ，x－x0］≦0，∀ξ∈∂ψ(x0)。

定理3 (i)若ψ:X→R在x0∈X是拟凸，则ψ在x0是Ⅰ型近似拟凸;(ii)若ψ:X→R在x0∈X是Ⅱ型严格近似拟凸，则ψ在x0是Ⅰ型近似拟凸。

证明:由拟凸的定义和定义10－11，定理的证明是显然的。

3 最优性充分条件

接下来的两个定理分别给出了VP的局部拟有效解和局部有效解的最优性充分条件。

定理4 假设(1)－(3)在x0∈S成立，对λ，u，满足下面的条件:(i)λTf在x0是Ⅰ型近似拟凸;(ii)uTg在x0是Ⅱ型严格近似伪凸，则x0是VP的局部拟有效解。

证明:假设x0不是VP的局部拟有效解，则对任意β＞0和x0的任意邻域U，存在x∈U∩S，使得f(x)－f(x0)+βd(x，x0)∈ －{0}，即 f(x)≤f(x0)－ βd(x，x0)≤f(x0)。

故有λTf(x)≦λTf(x0)，其中λTe=1。由λTf在x0是Ⅰ型近似拟凸，则对任意c＞0，存在x0的邻域U0，使得对任意 x∈U0∩S，［ξ1，x － x0］－ cd(x，x0)≦0，∀ξ1∈∂λTf(x0)。由条件(1)，取 U=U0，ξ2∈∂uTg(x0)和ξ3∈∂(βd(x，x0))|x=x0，结合上式有［ξ2+ ξ3，x － x0］+cd(x，x0)≧0。而由 ξ3∈∂(βd(x，x0))|x=x0可得，［ξ3，x－x0］≦βd(x，x0)。因此［ξ2，x －x0］+βd(x，x0)+cd(x，x0)≧0。

即［ξ2，x－x0］+αd(x，x0)≧0，其中 α =β+c。再由 uTg在 x0是Ⅱ型严格近似伪凸可得 uTg(x)＞uTg(x0)。

由条件(2)可得，uTg(x)＞0，矛盾。故x0是(VP)的局部拟有效解。

定理5 设条件(1)－(3)在x0∈S，对λ∈，u∈，满足下面的条件:

(i)λTf在x0是Ⅱ型严格近似拟凸;(ii)uTg在x0是Ⅱ型严格近似伪凸，则x0是VP的局部有效解。

证明:假设x0不是(VP)的局部有效解，则对x0的任意邻域U，存在x∈U∩S使得f(x)≤f(x0)，故有λTf(x)≤ λTf(x0)＜ λTf(x0)+cd(x，x0)，∀c ＞ 0。由条件(i)可得［ξ1，x － x0］≦0，∀ξ1∈ ∂λTf(x0)。再由(1)，取 ξ2∈ ∂()(x0)，ξ3∈ ∂(αd(x，x0))|x=x0，有［ξ2+ ξ3，x － x0］≧0。类似于定理4 的证明，可以导出矛盾，从而x0是(VP)的局部有效解。

［1］ WINKLER K.Characterizations of efficient points in convex vector optimization problems［J］.Mathematical Methods of Operations Research，2001(53):205-214

［2］VAZQUEZ F G，JONGEN H T，SHIKHMAN V，Todorov M I.Criteria for effciency in vector optimization［J］.Mathematical Methods of Operations Research，2009(70):35-46

［3］ZAFFARONI A.Degrees of efficiency and degrees of minimality［J］.SIAM Journal on Control and Optimization，2003(42):1071-1086

［4］GUPTA A，MEHRA B，Bhatia D.Approximate convexity in vector optimization［J］.Bulletin of the Australian Mathematical Society，2006(74):207-218

［5］BHATIA D，Gupta A，Arora P.Optimality via generalized approximate convexity and quasiefficiency［J］.Optimization Letters，DOI 10.1007/s11590-011-0402-3

［6］CLARKE F H.Optimization and nonsmooth snalysis［M］.New York:Willey-Inteerscience，1983

［7］HANSON M A，MOND B.Necessary and sufficient conditions in constrained optimization ［J］.Mathematical.Programming，1987(37):51-58