单目标机会约束规划逼近问题的稳定性分析

王俊林，霍永亮

(1.重庆师范大学数学学院，重庆401331;2.重庆文理学院 数学与统计学院，重庆永川402160)

机会约束规划由查纳斯(A.Charnes)和库伯(W.W.Cooper)于1959年提出，作为随机规划的一个分支，当问题介入的随机变量个数较多时，决定区域和期望中的多重积分求法比较难，使得非线性规划的许多算法失效，于是常利用某种逼近方法来求解随机规划问题［1］.由于概率的扰动性，这就产生了最优值与最优解集在数量与性质方面的稳定性问题.为了研究逼近解更好地接近初始问题的解，近年来有许多学者以各种形式构造机会约束规划问题的最优解集、有效解集及弱有效解集的逼近方法.其中文献［2］基于切平面的产生及算法研究了非线性机会约束规划的最优解;文献［3］以概率测度的某种收敛性分析随机规划问题逼近最优解的稳定性，得到了逼近解的一些相关结论;文献［4，5］对随机规划逼近问题作了一些稳定性分析;文献［6］提出概率约束规划的概率目标模型并以一种逼近算法求解，讨论了其算法的有效性;文献［8，9］研究了随机规划的上图收敛及方法等.关于机会约束规划问题逼近的稳定性方向，此处在文献［3，7，12-14］的启发下从单目标机会约束规划问题最优值函数着手，以分布收敛、K-收敛、上图收敛、上半收敛等工具进一步分析了问题的逼近解及其稳定性.

考虑如下单目标机会约束规划模型:

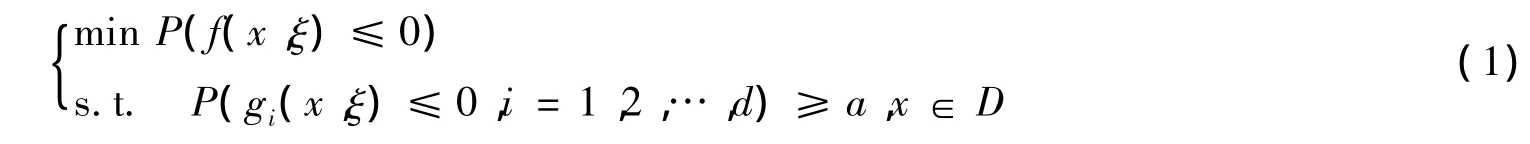
其中，x=(x1，x2，…，xN)T∈RN，ξ为定义在完备型概率空间(Ω，F，P)上的m维连续随机向量，确定性约束集D⊂RN是紧致的，B(RN)表示RN中的Borel子集全体，P是定义在B(RN)上的概率测度全体，f:RN×Rm→R，g:RN×Rm→Rd，N为自然数全体.问题(1)的可行集、最优解集分别为S0和P0.

设{ξn}为ξ的离散化随机变量序列，且随机变量序列按分布收敛于ξ0，记作，则问题(1)的逼近模型为:

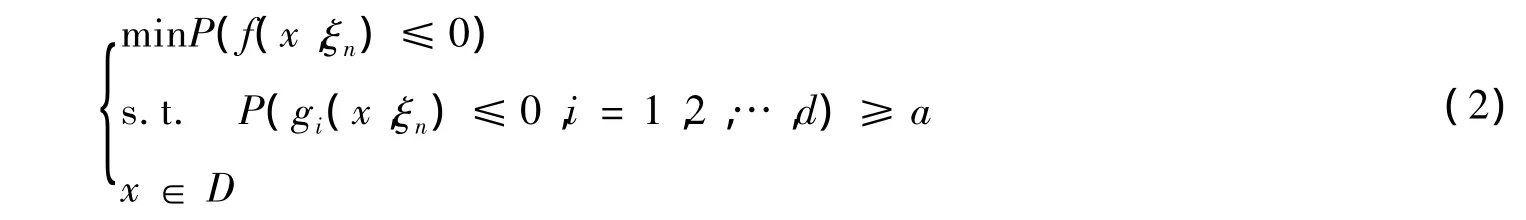
问题(2)的可行集和最优集分别记为Sn和Pn.

于是问题(1)和(2)转化成了与其等价的确定性机会约束规划模型:

则问题(3)的目标函数、可行集及最优解集记为Q(x，μ0)，S(μ0)及P(μ0);问题(4)的目标函数、可行集及最优解集记为 Q(x，μn)，S(μn)及 P(μn).

于是由问题(3)和(4)可以得到无约束的规划型问题(5)和(6)

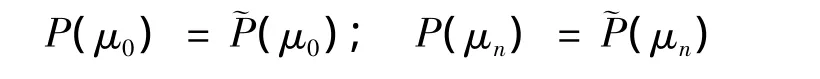
主要以函数的上图收敛、上半收敛等刻划逼近问题最优解集的稳定性，考虑到等价于μ，于是问题(2)逼近(1)的最优解就等价于问题(6)逼近(5)的最优解.

1 上图收敛

引理1 设{μ0;μn，n∈N}为B(RN)上的概率测度族，则下列条件等价:

(2)对任意的{An，n∈N}⊂B(RN)，且(An)≤μ0(A0).

(3)对任意的{An，n∈N}⊂B(RN)，且(An)≥μ0(A0).

证明 参见文献［3］的定理1.1.

定义 1［3］令:

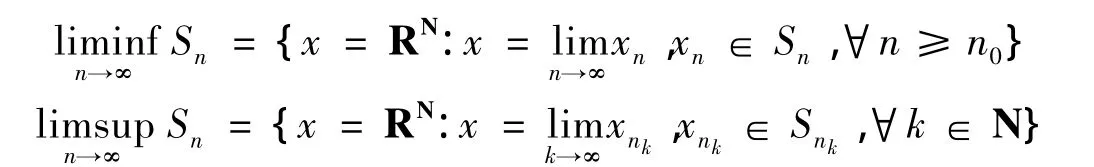
定义2［10］称集合 S(μ)是正则的，指 S(μ)=cl S(μ)°，且 S(μ)°≠∅，其中 cl表示闭包，S(μ)°=00000{x∈D⊂RN:μ0(h(x))-α ＞0}.

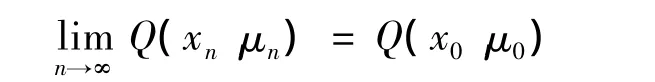
证明 要证Q(xn，μn)在D×Rm上连续，即要证其在D×Rm内上半连续且下半连续.

情形1 当f(x，ξ)在D×Rm上下半连续时，设x0∈D且xn→x0，令 ξ0H(xn)，其中

(2)对每个给定的 x∈RN，μ0(N(x))=0.其中 N(x)={μ∈Rm:gi(x，μ)=0，i=1，2，…，d}.

(3)S(μ0)=cl S(μ0)°，且 S(μ0)°≠∅.

则 i)存在N0，当n≥N0时，S(μn)是非空紧集.

证明 i)由定理1的(3)可知 S(μ0)°≠∅.令任意 x0∈S(μ0)°，x0∈D 且 μ0(h(x0))-α ＞0，设 β=μ0(h(x0))-α，即 β ＞0，由定理1 的(2)知对每个固定的 x0∈RN，有 μ0(N(x0))=0，又由文献［3］，定理5.6可知，对任意给定ε＞0，使得0＜ε＜β时，存在N0，当n≥N0时，有

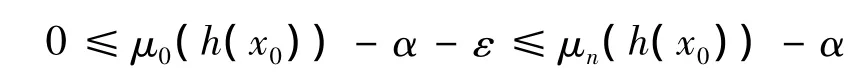
于是当 n≥N0时，有 x0∈S(μn)，即 S(μ0)°⊂S(μn)⊂D，由 D 的紧性知，Sn是非空紧集.

ii)由gi(x，μ)(i=1，2，…，d)在RN×Rm上连续及S(μn)⊂S(μ0).下证:S(μ0)).不妨设 x0∈S(μ0)，由可行集 S(μ0)为正则的，则必存在{zn}⊂S(μ0)°，使得 zn→x0，由 i)的证明过程可知，对∀zn，∃Nn时，有zn∈S(μn)，于是可以构造如下数列:

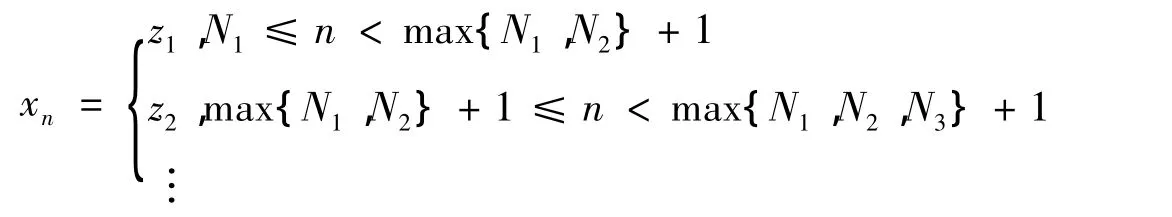
从序列的构造可得，对所有的 n≥N1，有 xn∈S(μn).又由 zn→x0，故 x0，于是由定义 1 可知

定义 3［9，10］设函数序列{f:RN×Rm→∈N}和函数 f:RN×，若有

i)对∀x0∈RN，xn→x0，有)≥f(x0).

ii)对∀x0∈RN，∃xn→x0，有)≤f(x0).

则称函数序列{fn:RN×Rm→R，n∈N}上图收敛于f:RN×Rm→R，记

定理2 设对任意 i∈{1，2，…，d}，gi(x，μ)在 D × Rm上下半连续，对给定的 x，gi(x，ξ)，关于 μ 上半连续，且满足:

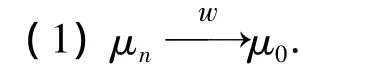
(2)对每个给定的 x∈RN，μ0(N(x))=0.其中 N(x)={μ∈Rm:gi(x，μ)=0，i=1，2，…，d}.

(3)S(μ0)=clS(μ0)°，且 S(μ0)°≠∅.

不妨设x0∈RN，由D的紧致性知，必存在xn→x0，接着对x0∈RN以下两种情形讨论:

① 若 x0∈S(μ0)，并且 xn→x0，由 δS(x)的定义有:

② 若 x0∉S(μ0)，并且 xn→x0，则必存在 N，当 n≥N 时，有 xn∉S(μn).否则，存在{nk}，使得 xnk∈S(μnk)，且xnk→x0.由，则x0∈S(μ0)，这与x0∉S(μ0)矛盾.于是由δS(x)的定义知:

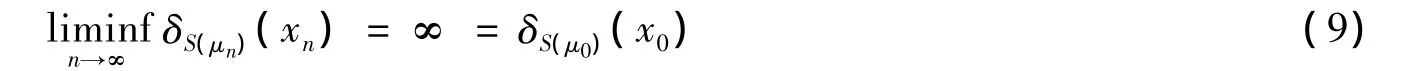
根据(8)(9)两式知定义3(i)成立.

同理，设x0∈RN，面对其亦分两种情形讨论:

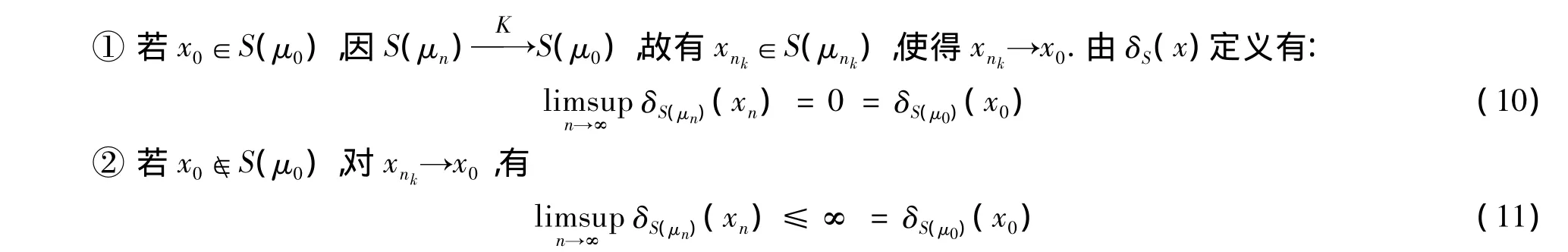
由(10)(11)两式知定义3(ii)成立，综合式(8)(11)，结论成立，证毕.

2 最优解集的上半收敛性

定义 4［14］如果)=0，则称集合序列{S}上半收敛于 S.其中上半距离 e(A，B)=n0.集合 A⊂RN，B⊂RN，RN为 N 维欧氏空间.

定理3 设f(x，ξ)在 D ×Rm上连续;对任意 i∈{1，2，…，d}，gi(x，μ)在 D ×Rm上下半连续;对给定的x，gi(x，μ)关于 μ 上半连续，满足:

则问题(6)的最优解集序列{~P(μn)}上半收敛于式(5)的最优解~P(μ0).

因S(μ0)是正则，故存在n0，当n＞n0时，P~(μn)≠∅，利用文献［9］，定理7及式(12)可知，要证明最优解集{P~(μn)}上半收敛于 P~(μ0)，即)，P~(μ0))=0，需证:∀ε ＞0，∃N0，当 n≥N0时，有 P~(μn)⊂P~(μ0)+Bε(0)，其中 Bε(0)={x∈RN:x-0 ＜ε}.下证:对任意的开集 V 且 P~(μ0)⊂V，∃N0，当 n≥N0时，有P~(μn)⊂V，假设此结论不成立，则必存在序列{xn}，使得xn∈P~(μn)且xn∉V，因 P~(μn)⊂D和D的紧kkkkk性，序列{xnk}必存在聚点x0，又由V是开集，故x0∉V，另外由文献［10］的定理4及文献［11］命题3.3知，x0∈P~(μ0)，这与 P~(μ0)⊂V 矛盾.特别地，取 V=P~(μ0)+Bε(0).证毕.

推论1 设f(x，ξ)在 D ×Rm上有界连续，且对任意 i∈{1，2，…，d}，gi(x，μ)在 D ×Rm上有界下半连续;对给定的x，gi(x，μ)有界且关于μ上半连续，满足:

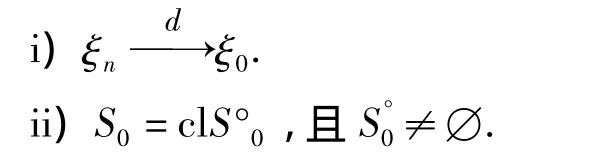
则问题(4)的最优解集序列{P(μn)}上半收敛于(3)的最优解P(μ0).

证明 考虑到条件中f(x，ξn)在D×Rm上的有界性及等价于应用定理3知，对任意 i∈{1，2，…，d}，问题(4)的最优解集序列{P(μn)}上半收敛于式(3)的最优解 P(μ0).

［1］骆建文，鲁世杰.概率约束规划的稳定性分析［J］.高校应用数学学报，2001，16(1):119-124

［2］WEINTRAUB A.A cuting plane approach for chance constrained linear programs［J］.operations research，1991，39(5):776-785

［3］霍永亮.随机规划稳定性理论［M］.成都:西南交通大学出版社，2010

［4］骆建文，鲁世杰.随机规划逼近解的收敛性［J］.浙江大学学报，2000，16(4):15-20

［6］张克邦，黄炳章.概率约束规划的概率目标模型及其解法［J］.上海交通大学学报，1992，26(1):90-95

［5］DENTCHEVA D，HENRION R，RUSZCZYNSKI A.Stability and sensitivity of optimi-zation problems with first order stochastic dominance constraints［J］.Society for industrial and applied Mathmatics，2007，18(1):322-337

［7］RÖMISCH W，SCHULTZ R.STABILITY ANALYSISFOR STOCHASTIC PROGRAMS［J］.Annals of Operations Research，1992(30):241-266

［8］ ZERVOS M.ON THE EPICONVERGENCE OF STOCHASTIC OPTIMIZATION PROBLEMS［J］.Mathematics of Operations Research，1999(2):495-508

［9］ PENNANEN T，KOIVN M.Epi-covergent discretizations of stochastic programs via integration quadratures［J］.Numerische Mathematic，2005，100(1):141-163

［10］霍永亮，刘三阳.随机规划逼近最优解集的上半收敛性［J］.西安电子科技大学学报，2005，36(6):953-957

［11］DUPACOVA J，WETSR J B.Asymptotic Behavior of Statistical Estimators of Optimal Solutions of Optimiation Problems［J］.the Annals of statistics，1998，16(1):1517-1549

［12］SALINETTI G.Approximations for chance constrained programming problems［J］.Stochastic，1983(10):157-179

［13］KUCHLER C.On stability of multistage stochastic programs［J］.Society for industrial and applied Mathmatics，2008，19(2):952-968