An analytical model for predicting battery lifetime

Guang Yang, Sangho Kim, Seongsoo Lee

(SoC Laboratory, Soongsil University, Seoul156-743，Korea)

An analytical model for predicting battery lifetime

Guang Yang, Sangho Kim, Seongsoo Lee

(SoC Laboratory, Soongsil University, Seoul156-743，Korea)

We used an analytical high-level battery model to estimate the battery lifetime for a given load. The experimental results show that this model to predict battery lifetime under variable loads is more appropriate than that under constant loads.

battery modeling；battery lifetime prediction；constant load；variable load

As is well known to us, normal operations of modern portable electronic devices, such as most laptops, handheld PCs, digital cameras, displays, mobile phones, wireless network interfaces, and so on, depend on the enough supply of battery power. If the battery becomes fully discharged, all of them will go off-line. Furthermore, the progress of these electronic devices and systems is ever-changing, and battery technologies have a long distance with amazing increasing of power demands. Therefore, it is undoubtedly that one of key points of battery technologies is to estimate the battery lifetime which has special important and necessary technics in the course of battery research and design.

Here, the lifetime, or time-or-failure, of the battery is the time when it becomes fully discharged[1]. In other words, it is the total time of one discharge process from full-charged to full-discharged. The constant load refers to its current being basically considered to maintain constant and invariable as time goes on. On the contrary, the variable load refers to its current being considered to change dynamically with time. The battery lifetime depends mostly on its capacity and the level of the load applied to it. Modeling of batteries is very difficult because of non-linearity of charge delivery. Even so, for accurate estimation of battery lifetime, many researches have been done in various battery models, such as physical models, empirical models, analytical models, and the ultimately purpose of applying them is to representative load profiles. However, many accurate low-level models[2-3]based on the differential equations that describe the complex phenomena coming up in an electrochemical cell have been around for about a decade, but solving these equations have to take many days. In recent years, however, several researches have been done in high-level battery models[1,4-5]that shorten simulation time while predicting relevant variables with acceptable accuracy[6].

One of the typical and famous representative high-level battery modelling for predicting battery lifetime is the Rakhmatov and Vrudhula battery modeling which is further and extended development of basing on empirical Peukert's law[7]: a=IbL. Here, a and b are the appropriate parameters for given battery; I is the discharging current; L is the battery lifetime. In general, we use the analytical modeling to predict battery lifetime under all kinds of loads, whether constant or variable. However, we actually can know through the massive experimental contrast results: the modeling prefers to predict battery lifetime when the loads are variable.

The goal of this paper is to verify an accurate battery lifetime estimation method under variable loads. The remainder of the paper is organized as follows. Section 2 describes the theory of our analytical high-level battery modeling; Section 3 describes experimental setup and environment; Section 4 presents the analysis of the experimental results that suggest the final result of verification; and, finally, Section 5 concludes the paper.

1 Battery modeling

From a general survey of the development course of battery models, they can be roughly classified into four types: physical models, empirical models, abstract models and mixed models. Every kind of models should be appraised of four basic aspects: accuracy, computational complexity, configuration effort and analytical insight[6].

Just as we know it, low-level models are all established on the basic of quite complex partial differential equations to describe the process of discharge which directly leads to excessive long simulation. Therefore, researches have presented a few of high-level simulation based on models which reduce the amount of simulation time required and also demonstrate fairly precision.

Next, let's take a briefly look at related models on high-level simulation. These models have been done influential researches including the Rakhmatov and Vrudhula analytical model[1], the discrete-time VHDL model[8]and the stochastic model[9]. As far as the battery lifetime prediction is concerned, all of them have certain universality. Nevertheless, the last two models fail to supply a methodic equation to estimate the battery lifetime. In addition, in the process of simulation, all kinds of parameter features are not easily installed. However, Rakhmatov and Vrudhula presented a simplistic equivalent equation with the true battery, and then obtained analytical equation.

Rakhmatov and Vrudhula battery modeling is mainly applicable to lithium-ion batteries. To be specific, Li-ion battery is composed of anode, cathode and electrolyte, and two electrodes are separated by the electrolyte. During the process of discharging, anode releases electrons traveling round the external circuit, meanwhile cathode receives these electrons from the circuit. Rakhmatov and Vrudhula abstracted the moving of electro-active material in the electrochemical reaction into one-dimensional diffusion problem on a limited area which is on the basis of some physical laws, such as Farady's law for describing electrochemical reduction and Fick's law for describing the features of one-dimensional diffusion around inside a battery. Through a series of the derivation and calculation, they obtained the extension of Peukert, which shows the relation between the load current I and the battery lifetime L as

where a and b are the appropriate parameters for the given battery. The physical interpretation of parameter a is the maximum capacity of the battery. Parameter b indicates the rate of dynamical current loads at the surface of the electrode that are compensated, which can be used to evaluate the discharging characteristics of the batteries. In general, the higher the parameter b value, the better the battery discharging characteristics. In addition, if n=1, Eq.(1) is cut short for the Peukert's law: a=IbL.

From Ref.[1], we can learn that the analytical battery model can make accurate prediction lithium-ion batteries lifetime for any given type of loads. However, in this paper, our further experiments suggests that the analytical model has more accurate result in variable loads case than that in constant loads case.

2 Experimental setup

To verify the following conclusion, a simulation based on the experimental setup was established. A white iPad was considered to supply a typical application load voltage, current profile and runtime which would be supported by Eq.(1).

We use the experimental setup to get the voltage and current profile, respectively, as shown in Fig.1. In this experiment, the 2 400 mAh ICR 18650-24E battery is feeding power to the device iPad. Once the battery is completely exhausted, the device will turn off immediately. In addition, we make the good choice from two movies, of which one is a dynamic, active and fierce video rapidly changing current equivalent to the type of the variable load, and the other is a soft, quite and flat video basically holding constant equivalent to the type of the constant load.

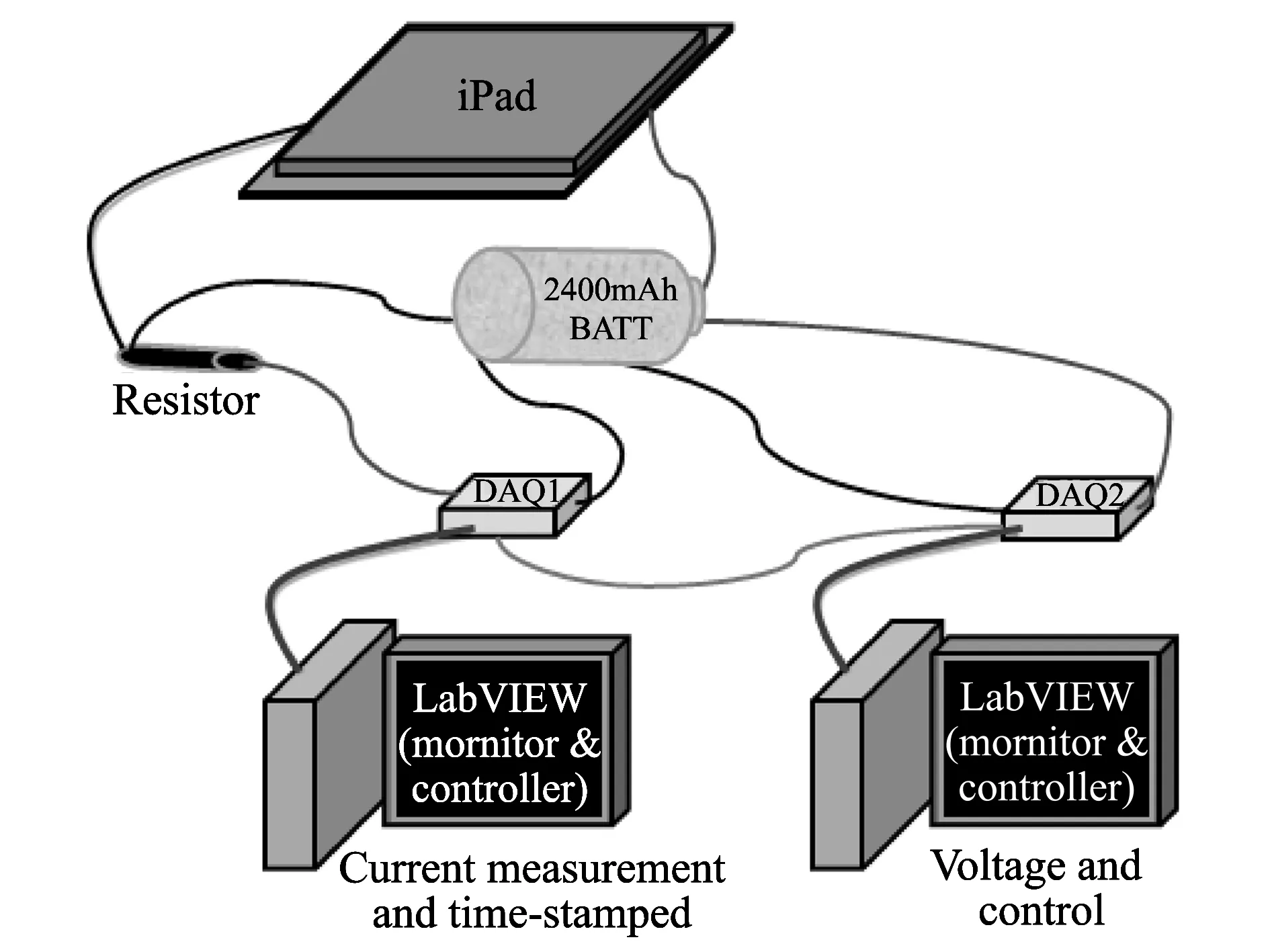
Fig.1 Actual experimental environment

We adopt the National Instruments data acquisition device (DAQ) to obtain the related information, including voltage, current from the iPad, and prediction and elapsed time of the battery. It is worth emphasizing that the current to be measured is often necessary to connect a small resistance shunt about 119 mΩ. The last requires a bit of explanation that the related control program written in graphic program language (G Language) which is fundamental of laboratory virtual instruments engineering workbench (LabVIEW) in the computer tracking the voltage and current profiles are sampled every one second until the battery is totally discharged, namely, the device stops working.

3 Experimental results

The experimental results are listed in Table 1 and Table 2 which show seven results with two cases, constant loads and variable loads. Every table separately includes the battery of prediction time, elapsed time, and the maximum and minimum deviation value between the two. Comparing the two tables, it is not difficult to find that emulation at the dynamic current case has a smaller error in battery lifetime prediction from a real system. Particularly, there are many maximum deviations which reach more than three-thousand seconds despite some of the minimum deviations showing a little better.

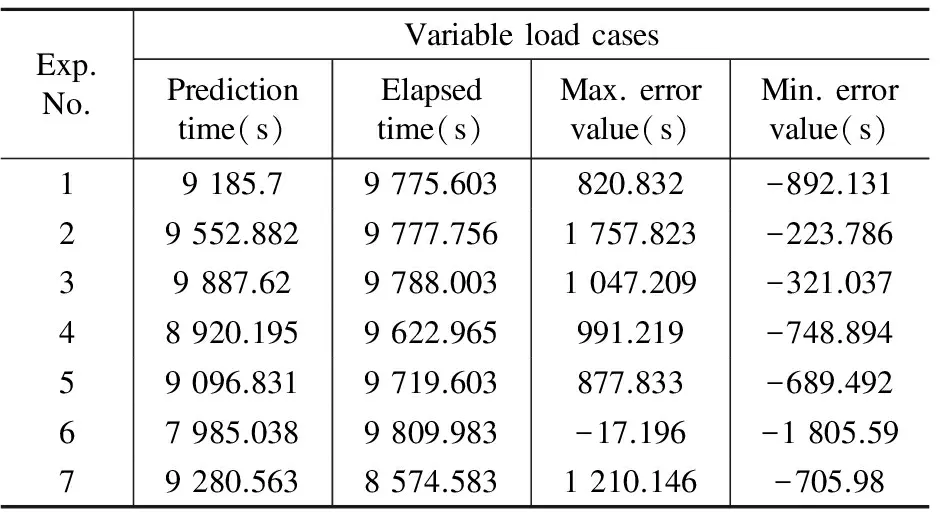
Table 1 Comparison of prediction time and elapsed time for variable loads

Table 2 Comparison of prediction time and elapsed time for constant loads

Finally, we show the experimental comparison chart of the elapsed time and prediction time for variable loads and constant loads, respectively, in Figs.2 and 3. The result can be intuitively observed from two charts. From the overall point of the battery lifetime prediction, these data from the variable load can obviously provide more accurate to the actual battery lifetime.

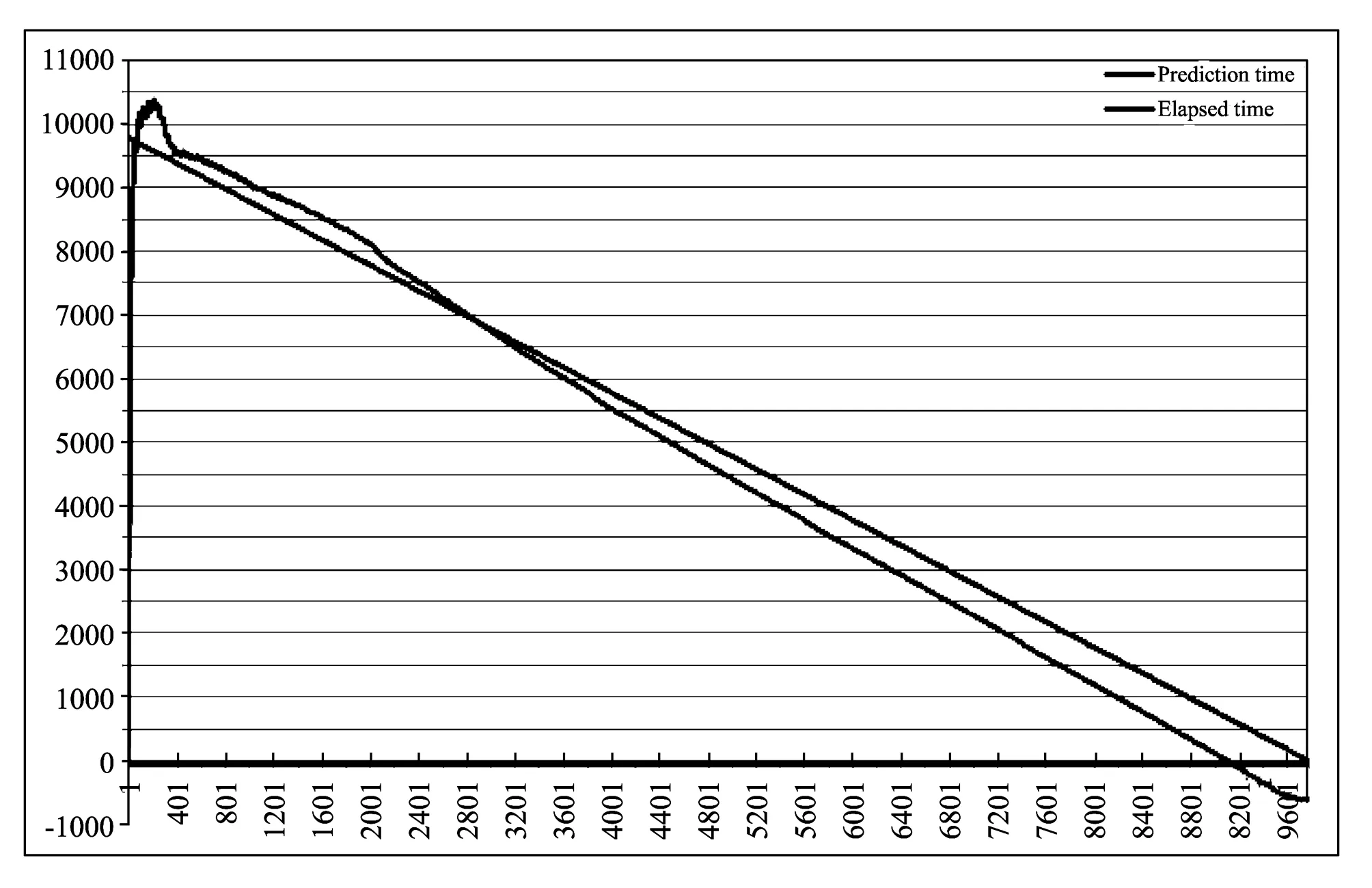
Fig.2 Comparison of prediction time and elapsed time for the variable load case

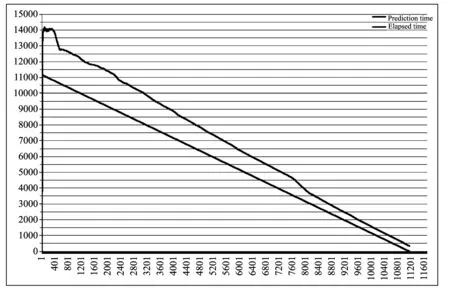
Fig.3 Comparison of prediction time and elapsed time for the constant load case

4 Conclusion

Based on an analytical high-level battery model for prediction, lithium-ion battery lifetime under variable loads and constant loads is discussed in this paper. Furthermore, through the series of the comparison of experimental results, we verified that it has a very good approximation of the real-world battery lifetime when the battery discharged through the model of non-constant current.

[1] Rakhmatov D N, Vrudhula S B K. An analytical high-level battery model for use in energy management of portable electric systems. In: Proceedings of 2001 IEEE/ACM International Conference on Computer Aided Design, 2001: 488-493.

[2] Doyle M, Fuller T F, Newman J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. Journal of the Electrochemical Society, 1993, 140(6): 1526-1533.

[3] Botte G G, Subramanian V R, White R E. Mathematical modeling of secondary lithium batteries. Electrochimica Acta, 2000, 45(15/16): 2595-2609.

[4] Pedram M, WU Qing. Design considerations for battery-powered electronics. In: Proceedings of the 36th ACM/IEEE Design Automation Conference, ACM Press, 1999: 861-866.

[5] Chiasserini C F, Rao R R. Energy efficient battery management. IEEE Journal on Selected Areas in Communications, 2001, 19(7): 1235-1245.

[6] Rao R, Vrudhula S, Rakhmatov D N. Battery modeling for energy-aware system design. Computer, 2003, 36(12): 77-87.

[7] Linden D, Reddy M. Handbook of batteries. 3rd edition. McGraw-Hill, 2001

[8] Gold S. A pspice macromodel for lithium-ion batteries. In: Proceedings of 20th Annual Battery Conference on Applications and Advances, 1997: 215-222.

[9] Panigrahi T D, Panigrahi D, Chiasserini C, et al. Battery life estimation of mobile embedded systems. In: Proceedings of the 14th International Conference on VLSI Design, 2001: 57-63.

date： 2012-08-21

The MKE (the Ministry of Knowledge Economy), Korea, under the ITRC (Information Technology Research Center) support program supervised by the NIPA (National IT Industry Promotion Agency) (NIPA-2011-C1090-1021-0010); Seoul Metropolitan Government, under the Seoul R ＆ BD Program supervised by Seoul Business Agency (No.ST110039)

Seongsoo Lee (sslee@ssu.ac.kr)

CLD number： TM910.1 Document code： A

1674-8042(2013)01-0019-04

10.3969/j.issn.1674-8042.2013.01.005