几乎周期点稠密系统的研究

付 瑶，李 楠，范钦杰

（1.吉林师范大学 数学学院，吉林 四平 136000；2.吉林师范大学 博达学院，吉林 四平 136000）

0 引 言

1972年洛伦兹发表了《蝴蝶效应》的文章后，激发启了人们对混沌学研究的浓厚兴趣。混沌不仅是非线性系统普遍存在的现象，而且是非线性动力系统所固有的特性。同时，混沌学也不是独立存在的一门学科，它与其它各门科学之间相互依靠、相互促进。而且混沌是无处不在的，在实践生产中应用是非常广泛的。随着混沌理论研究的逐渐深入，拓扑熵大于零已经被广大学者作为刻画系统复杂程度的一个重要指标。它是迄今为止唯一的拓扑共轭数值不变量。并且在研究问题过程中也存在一定的局限性，所以仅仅用拓扑熵来刻画系统的复杂程度是不够的。于是广大学者开始把目光转移到了系统的中心测度上。

已有的成果表明：一个紧致系统全部重要的动力性态完全集中在它的测度中心上［1］，所以研究极小系统的性态就能够满足需要。从而在极小系统基础上，构建了几乎周期点稠密系统。这对更深入研究紧致动力系统的本质有重要地启示作用，也揭示了几乎周期点稠密集与Li－Yorke混沌的关系.

前期的研究成果已经对几乎周期点稠密系统的混沌性有了一个初步认识，经过对问题深入的探讨，笔者对这个系统的动力性态进行了进一步的研究。

1 基本概念

设X为紧致度量空间，f：X→X为从X到自身的连续映射。

定义1［2］称y∈X为x的ω极限点，如果存在正整数的子序列｛ni｝，使ni→∞。x的所有ω极限点的集合叫作x的ω极限集，记作ω（x，f）。

定义2［3］称x是几乎周期点的，如果对任意ε＞0，存在整数N＞0，使得对任何q≥0，存在整数r，q＜r≤q＋N满足d（fr（x），x）＜ε。f的全体几乎周期点的集合记作A（f）。

定义3［4］称M⊂X为（相对于f）极小集，如果M是f的非空不变闭集且M中不存在f的非空不变的真子集。如果X本身是极小的，则称f为极小映射。

定义4［5］称f为（拓扑）传递的，如果对X的任何非空开集U，V，存在n＞0，使得fn（U）∩V≠∅。称轨道在X中稠密的点为f的传递点。

定义5［6］设f是度量空间（X，d）到自身的连续映射，x，y∈X。如果满足：

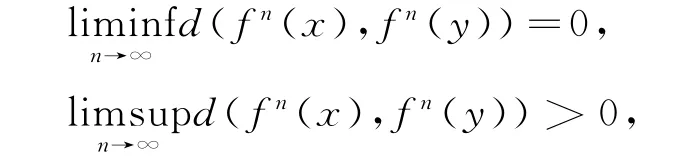
则称x，y为f的Li－yorke对；如果一个不少于两点的子集中任何不同两点均是f的Li－yorke对，则称该集合为f的Li－yorke混沌集，或简单地L－Y混沌集；如果f有一个由不可数多点构成的L－Y混沌集，则称它为Li－yorke混沌。

2 主要结论及证明

引理1［7］紧致系统（X，f）总存在极小集。

引理2［10］设M是X的非空闭子集且f（M）⊂M，则M极小当且仅当∀x∈M＝M。

引理3 设x∈A（f），则x∈A（f）当且仅当x∈ω（x，f）且x∈ω（x，f）是极小的。

证明见文献［8－9］。

引理4［10］下述条件等价：

1）f是极小的；

2）若ω（x，f）⊂X闭的，且对f不变，则ω（x，f）＝X或ω（x，f）＝∅。

证明 1）⇒2），设ω（x，f）⊂X闭，且对f不变。又设因此

2）⇒1），设x∈X。显然是X对f不变的非空闭子集是极小的。

引理5［10］若X紧致，则f传递当且仅当存在x∈X使得ω（x，f）＝X。

证明 令x∈X使得ω（x，f）＝X，同时，令U，V为X中的任意非空开子集。于是存在n＞m＞0，使得即有f是拓扑传递的。

另一方面令f是拓扑传递的。对任意的n＞0，存在半径为的有限多个开球覆盖X。当n取任意正整数时，所得这些开球覆盖可写成序列：U1，U2，…。对任意的正整数k，这个集合均是X的稠密开子集。因此知X是完备的，则根据Bairc纲定理［11］，存在。因为x的轨道穿过每个Uk，于是orb（x，f）在X中是稠密的。此时f拓扑传递蕴涵着f（X）＝X。则存在y∈X使得f（y）＝x。若y∈orb（x，f），则x是周期点且ω（x，f）＝X。否则y∈ω（x，f），这蕴涵x∈ω（x，f），于是ω（x，f）⊃orb（x，f）。进而这是因为ω（x，f）是闭集。从而也有ω（x，f）＝X。

定理1 设（X，f）为紧致系统，若x∈A（f）（x∈X）且＝X，则f中存在Li－Yorke混沌。

证明f：X→X是连续自映射：ω（x，f）→ω（x，f）的转移自映射＝X，而ω（x，f）由文献［12］中定理1说明存在SS混沌集。显然存在Li－Yorke混沌集。所以f中存在Li－Yorke混沌集，定理得证。

定理2 若几乎周期点稠密系统具有混合性，则该系统是Li－Yorke混沌的。

引理6［10］设（X，f）为紧致系统，则f是拓扑混合的，蕴涵f是Li－Yorke混沌的。

定理2的证明 根据引理6的叙述，显然知道定理2成立。

定理3 设（X，f）为紧致系统，若x∈A（f）（x∈X）且＝X，则f是拓扑遍历的。

证明 根据文献［13］中推论3显然可以得到f是拓扑传递的，设U，V是2个非空开子集，U，V∈（X，f），肯定∃n＞0，可以有f－n（U）∩V≠∅。由＝X知∃x∈A（f）∩f－n（U）∩V，即有x∈V满足fn（x）∈U。同时，根据f－n（U）的连续性可以判断，存在x的邻域D⊂V，使得f－n（D）⊂U。而且x∈X，x∈A（f），于是∃L使得即f是拓扑遍历的。

3 结 论

拓扑动力系统和遍历理论的研究是相辅相成的，其中一者研究的突破和进展或新思路新方法，必然促进另一者相关理论的发展。因为拓扑动力系统可以自然的视为一个保测系统；并且任何遍历系统都具备相应的拓扑表示。同时，它们的基础理论有很多着极为相似的表述。而且拓扑方法在研究中有其局限性。纯拓扑方法不能解决这类问题，但是应用遍历理论的有关知识和方法却可以对问题继续讨论。所以在研究问题时，对拓扑遍历性也进行了讨论。

以往的研究都是集中在对整个系统的动力性态上，而笔者的创新之处就在于研究系统中心测度的性质，从而推断整个系统的性质。于是经过努力证明了Li－Yorke混沌集在几乎周期点稠密系统中存在的条件；说明了混合的几乎周期点稠密系统的混沌性态；阐明了该系统的拓扑遍历性。同时在问题研究的过程中发现想要找到产生Li－Yorke混沌的充分必要条件并不容易，所以希望通过笔者的研究能够把已有的结果建立起联系，并简化相关的结论。

以往的研究都是集中在对整个系统的动力性态上，而笔者的创新之处就在于研究系统中心测度的性质，从而推断整个系统的性质。于是经过努力证明了Li－Yorke混沌集在几乎周期点稠密系统中存在的条件；说明了混合的几乎周期点稠密系统的混沌性态；阐明了该系统的拓扑遍历性。同时在问题研究的过程中发现想要找到产生Li－Yorke混沌的充分必要条件并不容易，所以希望通过笔者的研究能够把已有的结果建立起联系，并简化相关的结论。

［1］文兰.动力系统简介［J］.数学进展，2002，31（4）：293－294.

［2］麦结华，林桂莲.符号动力系统的若干性质［J］.广西大学学报，1993，18（3）：23－30.

［3］周作领，何伟弘.一致几乎周期点［J］.科学通报，1996，41（22）：2024－2026.

［4］廖公夫，范钦杰.混沌与SS混沌不等价［J］.数学年刊，2000，21A（6）：749－754.

［5］熊金城.拓扑传递系统中的混沌［J］.中国科学 A辑：数学，2005，35（3）：252－261.

［6］LI T Y，YORKE J.Period three implies chaos Amer［J］.Math Monthly，1975，82：985－992.

［7］LIAO Gongfu，WANG Liyan.Almost periodicity，chain recurrence and chaos［J］.Israel J Math，1996，93：145－156.

［8］ERDOS P，STONS A H.Some remarks on almost periodic transformations［J］.Bull Amer Math Soc，1945，51：126－130.

［9］GOTTSCHALK W H.Orbit－closure decom－positions and almost periodic properties［J］.Ibid，1944，50：915－919.

［10］周作领.符号动力系统［M］.上海：上海科技教育出版社，1997.

［11］MARTÍNE Q.Substitution dynamical systems－spectral analysis［M］.Berlin：Springer－Verlag，1987.

［12］廖公夫，范钦杰.拓扑熵为零且Schweizer－Smítal混沌的极小子转移［J］.中国科学：A辑，1997，27（1）：769－774.

［13］李楠.几乎周期点稠密的混沌性态［J］.长春大学学报，2011，21（2）：59－63.