一类非线性广义系统的精确线性化和极点配置一步设计

杨 光，武 帅

（沈阳师范大学 数学与系统科学学院，沈阳 110034）

0 引 言

非线性系统极点配置常用的方法是精确线性化和极点配置两步设计法［1］。因该法必须满足苛刻的对合条件，对于高于二阶的实际系统很难满足。文献［2］给出了回避苛刻对合条件的一步设计法，即对非线性系统精确线性化和极点配置一步完成。

到目前为止，有大量文献研究非线性系统的控制问题［3－8］，但针对非线性广义系统控制的研究仍然是个难题，本文将非线性系统的控制方法［2］应用到非线性广义系统的控制问题。首先给出将非满秩阵化为满秩阵的算法，然后求得非线性广义系统的状态空间实现；进而通过解一个拟线性PDEs（偏微分方程），利用Zubov's方法，完成该状态空间实现的精确线性化、极点配置一步设计，从而实现非线性广义系统的精确线性化、极点配置的一步控制。与以往常用的方法相比，无需满足严格的对合条件，精确线性化和极点配置两步由一个PDEs表达，且一步完成。使复杂的问题简单化。利用此方法解决Logistic增长的SIS传染病数学模型的一步控制问题，达到控制消除该传染病的目的。通过计算机仿真模拟表明：该方法有效可行。

1 非线性广义系统的状态空间实现

考虑如下多输出多输入非线性广义系统：

这里x∈Χ⊂Rn是系统的变量，z∈Ζ⊂Rp是系统的代数变量，X和Z是连通开集，u∈Rm是系统的控制输入，f（x）和k（x）是具有维数为n和p的光滑向量场，g（x）、c（x）、b（x）、l（x）分别为n×m、p×m、n×p、p×p阶光滑矩阵，h（x）为X→Rm的实解析函数。

定义1 对于广义系统（1），［l（x），c（x）］为非行满秩矩阵，通过对该系统中的代数方程求导，使得［l（x），c（x）］转化为行满秩的矩阵，最低求导次数称为广义系统（1）的阶数θd。

例如

假设广义系统（1）的阶数θd为有限的。

定义2 对于广义系统（1），如果通过算法可将 ［l（x），c（x）］转化为行满秩的矩阵，且存在一个反馈控制作用在系统（1）中得到一个正常系统，则称该正常系统为广义系统（1）的状态空间实现。

将 ［l（x），c（x）］转化为行满秩矩阵的算法如下：

设秩 ［l（x），c（x）］＝p1＜p，存在p×p阶可逆矩阵M1（x）使得

这里（x）、k1（x）分别为p1×p、（p－p1）×p阶矩阵。对k1（x）＝0求导，得到新的代数方程：

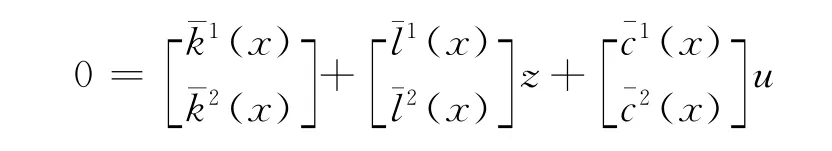
这里bj（x）、gj（x）分别表示矩阵b（x）、g（x）的第j列。

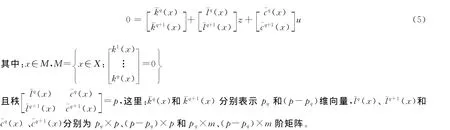
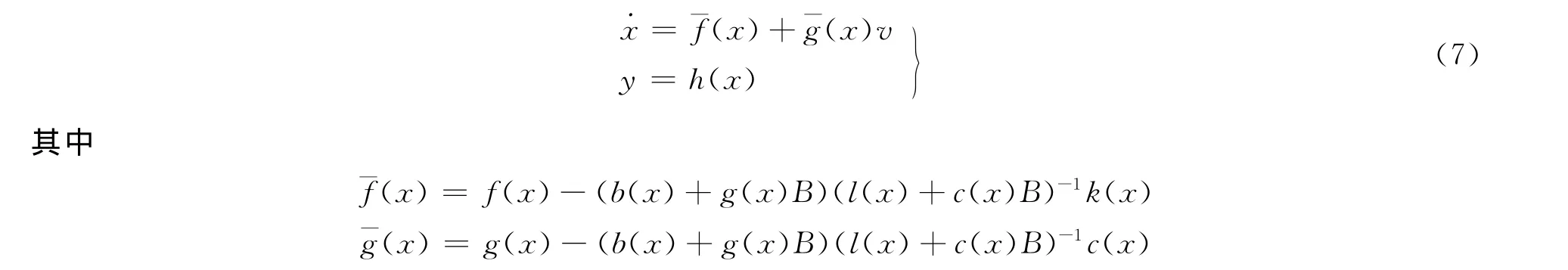
v为新的控制输入。

证明 存在p阶可逆阵P（x）使得

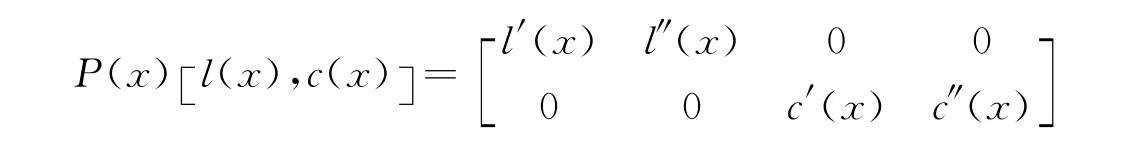
其中l′（x）、l″（x）、c′（x）、c″（x）分别为k×k、k×（p－k）、（p－k）×（p－k）、（p－k）×（m＋k－p）阶矩阵。不失一般性，假设l′（x）和c′（x）皆为可逆阵。

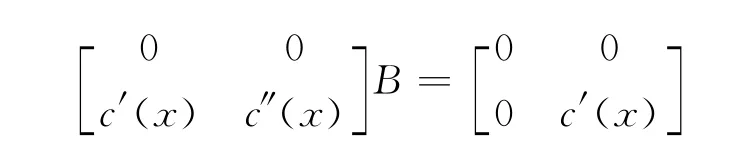
用P（x）分别左乘广义系统（1）中的代数方程得到：

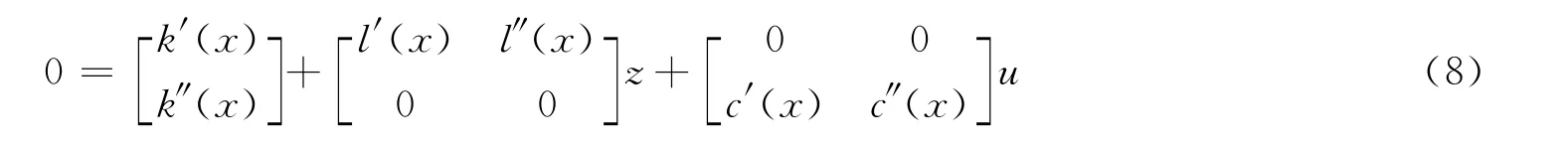
将反馈控制（6）代入式（8）中得到

将反馈控制（6）代入系统（1）中得到系统（7）。特别地，当秩 ［l（x），c（x）］＝秩 ［l（x）］＝p时，取B＝0，从而有代数变量表达式

将式（10）代入广义系统（1）中，得到如下非线性正常系统：

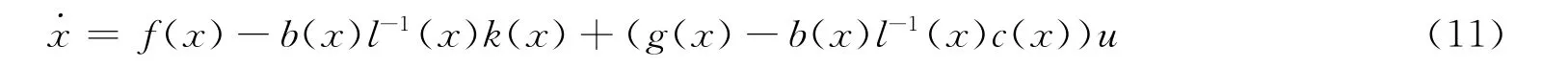
系统（11）为广义系统（1）的状态空间实现。

2 非线性广义系统精确线性化和极点配置一步控制

考虑如下系统

精确线性化和极点配置一步设计的方法就是利用坐标转移和寻找反馈控制律把非线性系统转化为线性的、能控的系统与极点配置一步完成［2］，而这一问题由解PDEs来实现。

假设存在一个可逆映射ξ＝w（x）和一个状态反馈u＝－Cw（x），则

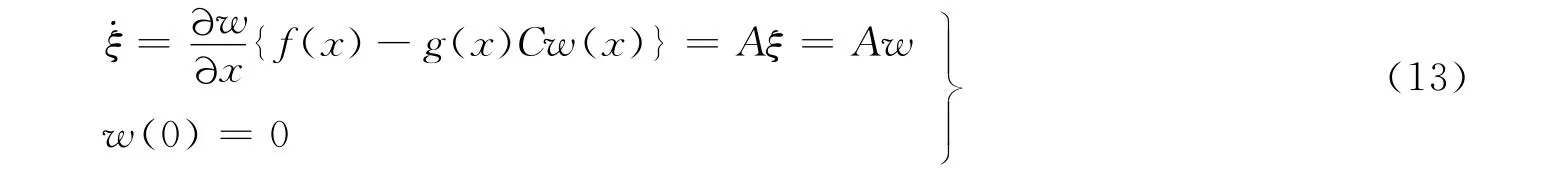
从而得到一次拟线性PDEs

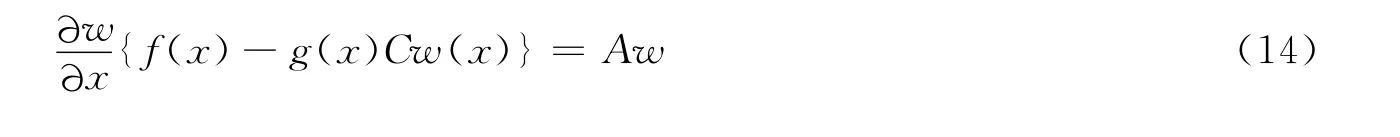
这里：C为m×n阶矩阵，w（x）∈Rn是式（14）的解，控制律

如果满足引理1的条件，该PDEs是可解的。

引理1［2］（Lyapunov's辅助定理）对于一次拟线性偏微方程：

其中：Φ（x，w）：Rn×Rn→Rn，Ψ（x，w）：Rn×Rn→Rn，w∈Rn→Rn为 PDEs（15）的解，n×n矩阵，0）（0，0）的特征值分别为k、γ（i＝1，2，…，n），且满足以下条件：ii

1）0 ∉CH｛k1，k2，…，kn｝，这里CH 代表一个凸包；

2）ki与γi线性无关，即对任意非负数mi，不满足

则PDEs（15）在平衡点x0＝0的邻域内一定存在唯一的解析解。

定理2 对于非线性广义系统（1）满足以下条件：

1）［l（x），c（x）］行满秩；

2）A＝diag（－λ1，－λ2，…，－λn），其中λ1，λ2，…，λn为正数；

①0∉CH｛η1，η2，…，ηn｝，这里CH 代表一个凸包；

②ηi与－λi线性无关，即对任意非负数mi不满足：

在平衡点x0＝0的邻域内一定存在唯一的解析解w（x）。

证明 因为已知条件1），由定理1可得：一定存在m×p阶矩阵B和u＝Bz＋v，使得［l（x）＋c（x）B］为满秩的，得到广义系统（1）的状态空间实现（7）。因为x0＝0、z0＝0为系统（1）平衡点，在平衡点处u＝0，显然f（0）＝0、k（0）＝0，系统（7）在平衡点处v0＝0。又因为当再利用已知条件2）、3），由引理1可知定理2中的结论成立，且有

由于w（x）含有调节参数λ1，λ2，…，λn，将v＝－w（x）代入系统（7）中，则该系统可写为如下形式：

其中

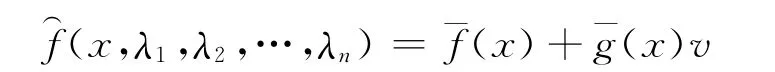
由已知条件2）可知A为 Hurwitz的，从而系统（18）在平衡点全局渐近稳定（x，λ1，λ2，…，λn）为Hurwitz的。从而实现了非线性系统（7）一步设计，进而实现了非线性广义系统（1）的精确线性化和极点配置一步设计。

3 Logistic增长的SIS模型一步控制

有些传染病如伤风感冒、痢疾等，愈后免疫力很低，也可视为无免疫力，染病者被治愈后变成易感者，易感者还可以感染成为染病者，这类疾病用SIS模型描述。如果种群总数量（或密度）N的变化满足Logistic模型［9］：

其中K为容纳量，不妨假设K＝1。则Logistic增长的SIS模型为

其中：x为易感者，y为染病者，N为种群总数量，a，b，γ，d为正常数，a为传染力，b为内禀自然增长率，γ为恢复率，d表示因为传染病而引起的死亡率。

引理3［9］区域且x＋y＝N≤1｝是系统（19）的正向不变集。如果a＞b＋γ＋d，则系统（19）在U内存在平衡点（0，0，0）、（1，0，1）和唯一正平衡点（~x，~y，~N），而且系统（19）在（1，0，1）是不稳定的。

由引理3知，当a＞b＋γ＋d时，此传染病将在该地区蔓延，要采取控制措施，使传染病在该地区消除，也就是使（1，0，1）成为稳定平衡点。控制系统如下：

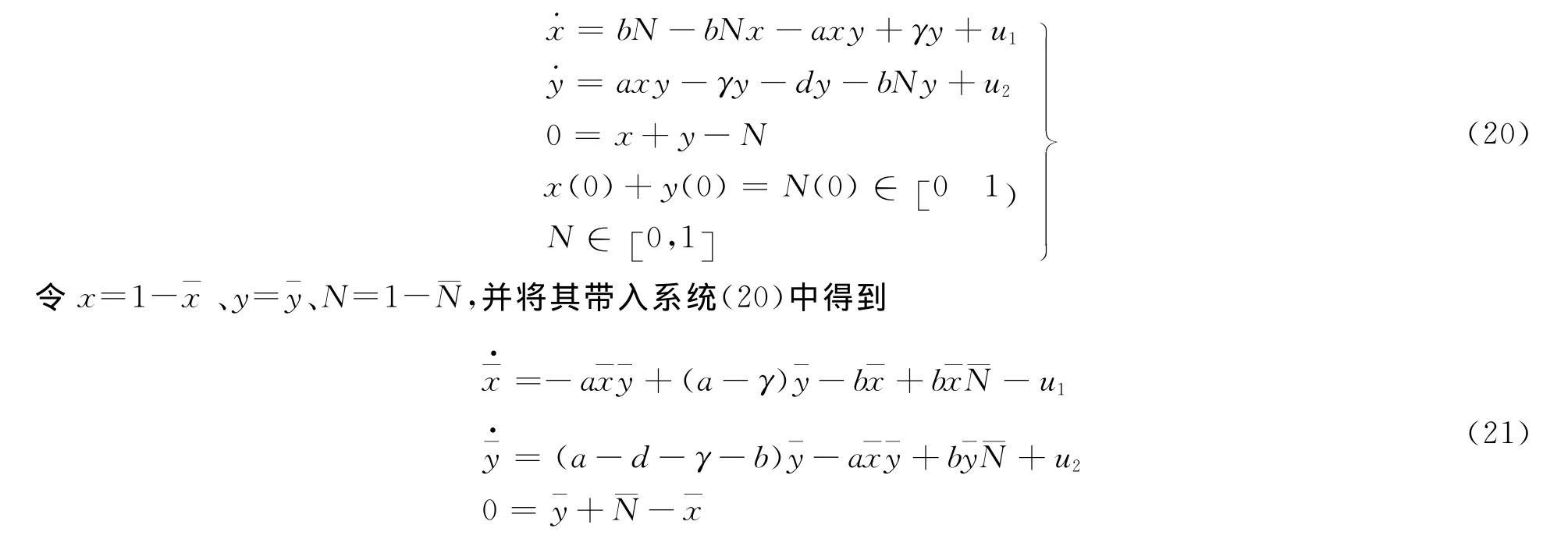
显而易见（0，0，0）为系统（21）的不稳定平衡点。

假设某地区流行一种传染病，其中a＝12，d＝0.001，γ＝10，b＝0.015，将系统（21）化为如下正常系统

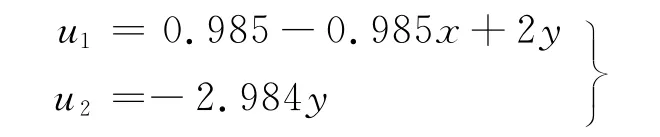
可见，施加上述控制在生物上就是对此传染病模型采取迁入易感者、隔离染病者、对易感者免疫、提高染病者的恢复率等措施，最终将该传染病消除。控制前与控制后染病者y（t）的情形如图1所示。实线表示染病者y（t）控制前随时间t的变化趋于平衡点，该传染病将会成为此地区的地方病；虚线表示染病者y（t）控制后随时间t的变化趋于原点，该传染病将灭绝。

图1 控制前与控制后染病者y（t）的情形

4 结 论

本文将非线性系统精确线性化和极点配值一步设计、Zubov's方法和最优化理论结合起来，应用于非线性广义系统的控制，一步设计与常用的两步法比，避免了严格的对合条件，特别是通过解一个系统的一阶拟线性奇异PDEs来实现一步设计。将此法应用于Logistic增长的SIS模型，仿真数据表明：该方法方便可行。

［1］AIBERTO I.Nonlinear Control systems［M］.London：Springer－Verlag，1995.

［2］KAZANTZIS N，KRAVARIS C.Singular PDEs and the single－step formulation of feedback linearization with pole placement［J］.Systems ＆ Control letters，2000，39（2）：115－122.

［3］CRESPO L G，SUN J Q.Stochastic optimal control of nonlinear systems via short－time Gaussian approximation and cell mapping［J］.Nonlinear Dynamics，2002，28（3／4）：323－342.

［4］CRESPO L G，SUN J Q.Stochastic optimal control of nonlinear systems via short－time Gaussian approximation and cell mapping［J］.Nonlinear Dynamics，2002，28（3／4）：323－342.

［5］GOHARY A E，BUKHARI F A.Optimal stabilization of steady－states of the genital herpes epidemic during infinite time intervals［J］.Appl Math comput，2003，137（11）：33－47.

［6］MATVEEV M A，SAVKIN A V.Application of optimal control theory to analysis of cancer chemotherapy regimens［J］.Systems ＆ Control Letters.2002，46（55）：311－321.

［7］CAULKINS J P，FEICHTINGERr G，GAVRILA C，et al.Dynamic cost－benefit analysis of drug substitution programs［J］.J Opt Theor Appl，2006，128（2）：279－294.

［8］KAZANTZIS N，KRAVARIS C，TSERONIS C，et al.Singular optimal controller tuning for nonlinear processes［J］.Automatics，2005，41：79－86.

［9］STEVAN D，NIKOLAOS K.A new Lyapunov design approach for nonlinear systems based on Zubov's method［J］.Automatics，2002，38：1999－2007.

［10］陈兰荪，陈键.非线性生物动力系统［M］.北京：科学出版社，1993.

［11］LIANG J R.Asymptotically stability and harmonic oscillation for singular nonlinear systems［J］.J Mathematical Research and Exposition，2002，22（1）：141－146.

［12］QI Y W，ZHANG X，SONG G D.Analysis of uncertain singular bilinear systems based on passivity theorem［C］∥Proceedings of the 27th Chinese Control Conference，2008：134－137.

［13］FENG Z S，FENG C Y.The invariance principle of singular nonlinear systems and its applications［C］∥World Congress on Computer Science and Information Engineering，2009：102－106.

［14］CLARKE F H，LEDYAEY Y S，STEM R J，et al.Nonsmooth Analysis and Control Theory［M］.New York：Springer，1998.

［15］DERIVIERE S，AZIZ－ZLAOUI M A.Estimation of attractors and synchronization of generatized Lorenz systems［J］.Applications and Algorithms，2003，10（6）：833－852.

［16］BACCIOTTI A，CERAGIOLI F.Nonsmooth optimal regulation and discontinuous stabilization［J］.Abstract and Applied Analysis，2003，20：1159－1195.

［17］JORGE C.Discontinuous dynamical systems［J］.IEEE Control Systems，Magzine，2008，28（3）：36－73.