基于离散元的节理硐室围岩数值模拟*

王红英 张 磊 郭 斌

(1.江苏建筑职业技术学院矿业与交通工程学院；2.国网技术学院；3.滨州市公路局高速公路养护中心)

基于离散元的节理硐室围岩数值模拟*

王红英1张 磊2郭 斌3

(1.江苏建筑职业技术学院矿业与交通工程学院；2.国网技术学院；3.滨州市公路局高速公路养护中心)

节理产状及其力学性能决定了岩体的完整状态，对硐室围岩整体稳定具有重要影响。考虑硐室建设过程中原岩应力释放率、节理间距、节理倾角及硐室埋深4个因素，采用离散元UDEC程序模拟了节理硐室围岩和支护结构受力状态。结果表明:①随着原岩应力释放率的增加，衬砌结构承担的荷载趋于减小，当释放率达到某一极限值时，会引起上覆岩体节理面整体错动、垮落，衬砌结构主要承载部位由仰拱向拱顶转移；②节理间距的增大增强了岩体的完整性，有助于增强岩体自身承载性能，提高围岩整体稳定；③节理倾角决定了衬砌结构主要受力部位；④随着埋深的增加衬砌结构内力及屈服单元数量总体呈增大趋势。

隧道 节理岩体 离散元 数值模拟 稳定性

岩土介质天然缺损严重，赋存方式多变，其间往往夹杂有各种各样的软弱节理面(如泥质夹层等)。这些软弱节理面分布范围相比围岩小得多，同样其强度也远远低于完整的岩块，这大大降低了工程岩体的完整性和整体强度，对节理岩体中硐室围岩承载、变形特性造成很大的影响。因此，节理岩体硐室围岩的变形比均质岩体要复杂得多，对工程岩体稳定状态的影响也起关键性作用。因此，节理岩体硐室围岩稳定性分析成为地下工程研究的一个热点［1-13］。

许多学者都开展了节理岩体硐室围岩的受力和变形特征相关研究:刘君等［8］分析了节理倾角对岩体应力分布、围岩变形及支护后衬砌变形与应力特点；冷先伦等［9］通过引入遍布节理模型，基于有限元方法分析了硐室围岩在莫尔－库仑模型和遍布节理模型2种条件下的位移、应力状态和塑性区发展情况；贺续文等［10］采用PFC讨论了节理连通率对边坡破坏形式的影响，指出随着连通率增大，其稳定性越来越差，边坡的破坏形式由局部崩塌转变为大范围的滑坡；郑颖人等［11］通过物理模型试验研究了节理倾角、节理间距对巷道稳定性的影响，结果表明节理倾角对围岩破裂模式影响显著，但对围岩安全系数影响较小；张承荣等［12］采用离散元方法研究了锚喷加固节理岩体局部危险带，结果表明锚喷支护是解决节理岩体支护的有效手段；赵景鹏［13］采用UDEC研究了节理倾角对大断面隧道围岩稳定性的影响，结果表明节理倾角优化锚杆支护角度及围岩破裂模式具有决定性作用；张志强等［14］基于UDEC数值模拟提出了以剪切滑移区范围作为评判节理岩体稳定性指标的方法。

综上可知，以往的研究大都仅限于某种特性节理岩体赋存条件下围岩的变形、应力及塑性区分布特征，很少综合考虑节理间距、节理倾角、硐室埋深及硐室开挖建设过程中围岩应力释放率多因素的影响。因此本研究基于上述4个节理特征因素，研究节理硐室围岩及支护结构的破坏及变形特征，为节理岩体加固设计提供理论依据和技术指导。

1 模型的建立

通用离散元程序(UDEC)是一个处理不连续介质的二维离散元程序，可用于模拟非连续介质(如岩体中的节理裂隙等)承受静载或动载作用下的响应。不连续面处理为块体间的边界面，允许块体沿不连续面发生较大位移和转动。变形块体被划分成有限个单元网格，且每一单元根据给定的本构模型；不连续面发生法向和切向的相对运动由“力－位移”关系控制。因此，UDEC能够很好地表征节理岩体的实际变形特性。

本研究中硐室围岩为Ⅳ类围岩，分布有正交2组节理；硐室几何形状为三心圆(宽8 m、高7.2 m)；计算范围取水平方向50 m、垂直方向40 m；支护结构采用锚喷支护体系。模型底部和两侧边限制法向位移，顶部施加相当于埋深的均布荷载(荷载取决于上覆岩体自重)，原岩应力为静水压力状态(水平侧压力系数取0.5)，计算模型如图1所示。岩体和节理均采用摩尔－库伦塑性模型，其力学参数见表1、表2，支护结构力学参数见表3、表4。

表1 岩石物理力学参数

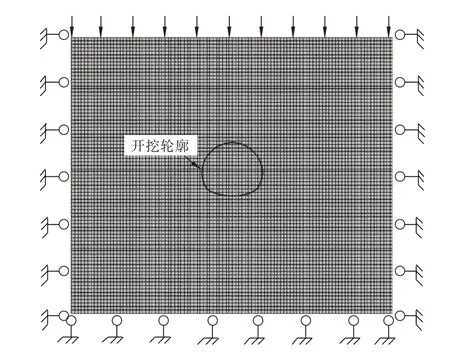
图1 计算模型

表2 节理物理力学指标

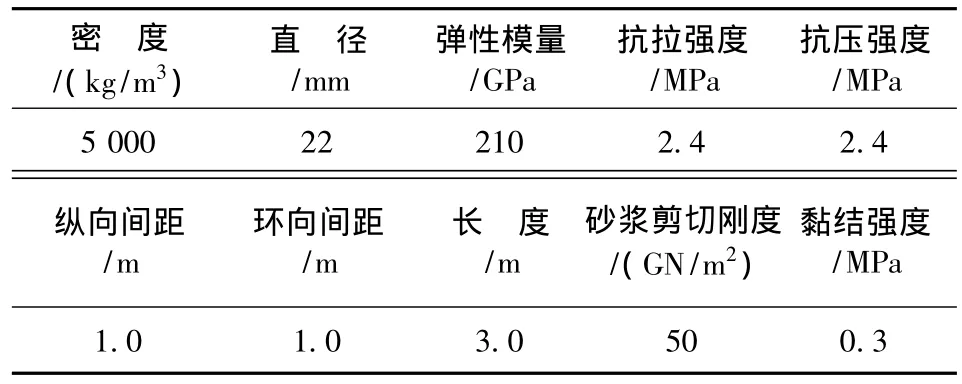
表3 锚杆参数

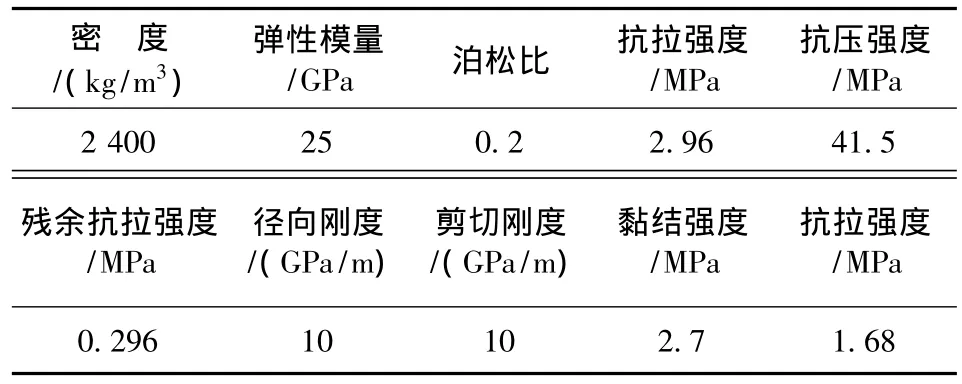
表4 钢纤维混凝土参数

2 计算结果

2.1 应力释放率的影响

隧道开挖是一个动态过程，围岩支护(锚杆、喷混泥土)是在隧道开挖后才施加的，也就是说围岩在施加支护之前就产生了一定的变形。研究发现，多达25%～75%的总变形(或总应力)已经在支护之前发生(释放)了。隧道开挖后锚喷支护时间对支护效果具有显著影响，因此，本研究用迭代时步来模拟隧道开挖后围岩暴露时间长短，围岩应力释放是随着变形的不断发展而逐渐进行的，应力释放率可按施作支护时的围岩位移与总位移的比值(位移释放率)确定［15］，即

式中，珋δ为围岩释放率；W为围岩位移释放率；λ为与地质条件和施工方法有关的参数，本文取0.7。本节分析中，节理倾角取0°～90°正交组，节理间距取0.5 m，埋深180 m。考虑应力释放量分别为0%、30%、60%和80%时进行锚喷支护，计算得到的喷射混凝土最大内力值见表5所示。

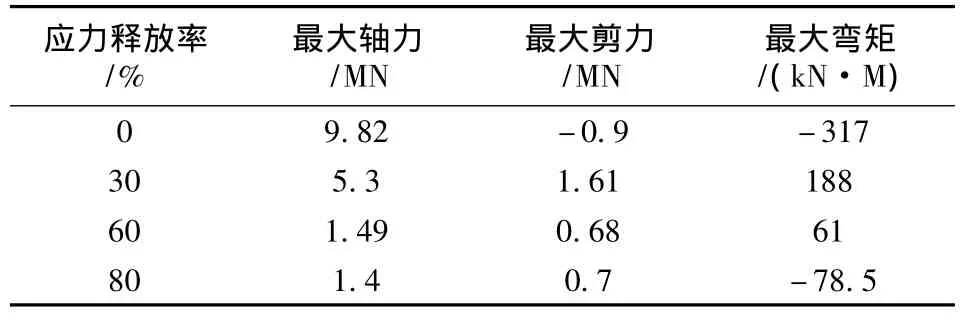
表5 不同应力释放率衬砌最大内力

对于完整性良好的岩体，硐室开挖后能够卸除岩体本身积聚的内能，有利于减小支护结构承担的荷载，保持工程岩体的稳定。但节理岩体应力释放，有可能会造成围岩自身的垮塌。理论上讲，在不引起节理岩体破坏的前提下适当进行应力释放减小支护结构承载是有利的。表5结果表明，随着应力释放率的增大，衬砌结构内力逐渐减小。

在应力释放率较低时屈服单元主要集中在仰拱部位，随着应力释放率的增加，屈服单元数量明显增多，且大都出现在拱顶部位，尤其是应力释放率达到60%时，屈服单元数量剧增。这主要由于节理面强度远远低于岩块，当围岩应力释放率大到一定程度便会引起节理面的错动、破坏，严重弱化岩体自身的完整性，并引起硐室上覆岩体的坍塌、垮落。上覆垮落岩体不仅丧失了自承载能力，而且其自身的重力作为一种新的附加荷载作用于支护结构，反而增加了支护结构承载负担。因此，合理的应力释放量应以不破坏节理面为前提。

2.2 节理间距对支护的影响

采用水平、垂直正交2组节理，埋深180 m，应力释放率为30%和60%。模拟节理间距为0.5、1.0、1.5、2.0、2.5 m时支护结构荷载受力情况。不同节理间距时模拟得到的围岩拱顶沉降、混凝土内力及屈服情况分别见图2和图3。

由图2可知，应力释放量较大时比应力释放量较小时拱顶总沉降量要大，这与上节得到的结果是相同的；施加衬砌后拱顶再下沉量在初始应力释放率分别为30%和60%时相差不大，这说明所施加的支护结构能够有效抑制围岩的进一步破坏；随着节理间距的增大，支护后拱顶下沉量和拱顶总下沉量总体呈减小的趋势。

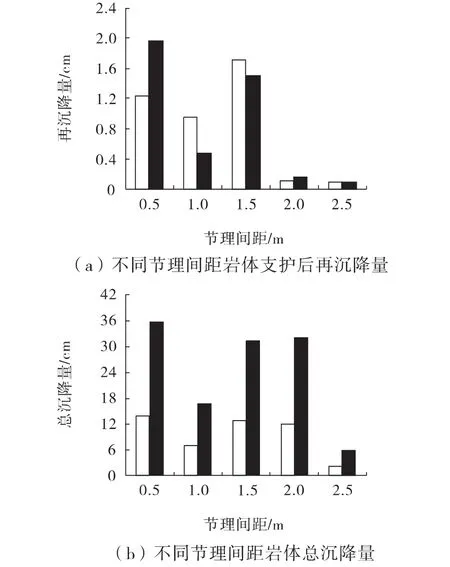
图2 不同节理间距岩体拱顶沉降量

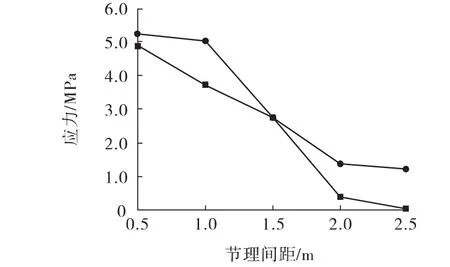
图3 不同节理间距衬砌应力状态

图3表明随着节理间距的增大，喷射混凝土轴力及屈服单元数量逐渐减小。节理间距从0.5 m增大到2.0 m时，大大减小了喷射混凝土承担的荷载，而当节理间距大于2.0 m后，节理间距的增加对喷射混凝土内力的减小不明显，这也正是工程尺寸效应的体现。因此，节理间距的增加大大增加了工程岩体的完整性，有利于其自身荷载承担荷载。

2.3 节理倾角对支护的影响

由于地壳运动的影响，节理岩体往往具有不同的倾角，而倾角对硐室围岩变形及应力分布都有决定性的作用。因此，需明确了解倾角对岩体稳定性的影响，以便对关键变形部位采取有效的加固措施。取应力释放率30%、埋深180 m、节理间距0.5 m，研究节理倾角在0°、90°，30°、120°和 75°、165°3 种组合情况下围岩及喷射混凝土内力分布。不同节理倾角下喷射混凝土最大内力及围岩变形分别见表6。

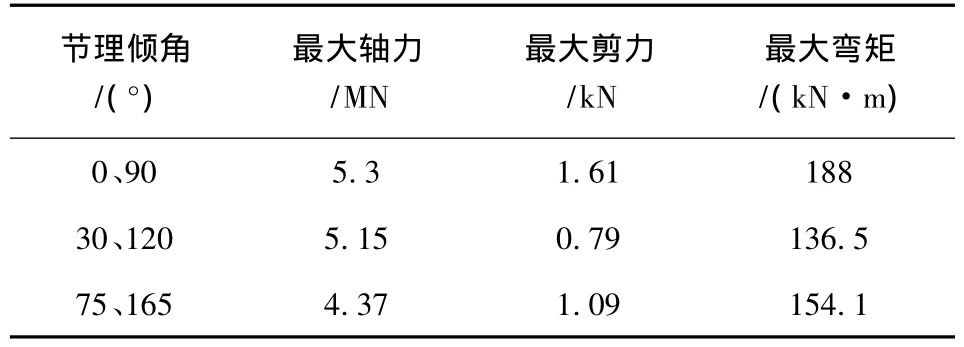
表6 不同节理倾角衬砌最大内力

从表6可以看出，当其他条件相同时，硐室围岩变形及衬砌内力受节理倾角影响较为明显。当正交节理组倾角为0°时，混凝土结构内力最大；而倾角为75°节理条件下，衬砌结构内力最小。因此，在进行地下硐室设计时，应充分考虑节理走向，最大程度地发挥其自身的承载性能。

图4为不同节理倾角时硐室喷射混凝土关键部位应力值。可以看出，两边墙位置喷射混凝土应力受节理倾角影响较小；仰拱部位在0°、90°时最小，在 75°、165°组合时内力最大；在 30°、120°节理岩体中，拱顶部位衬砌结构内力最小。因此，在不同倾角的节理岩体支护设计时，应就其容易产生破坏的薄弱部位加强支护，以保证硐室围岩的整体稳定。

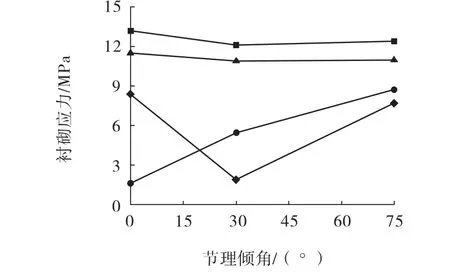
图4 不同节理倾角时衬砌应力

2.4 硐室埋深的影响

当地下工程埋深不同时，其变形破坏模式也不同。因此，考虑硐室埋深分别为 30、40、60、80、100、120、140和160 m时喷射混凝土受力和破坏情况。图5为不同埋深时喷射混凝土内力分布，可以看出随着埋深的增加衬砌结构内力也总体呈现增大的趋势。当埋深小于100 m时，随着埋深的增加衬砌结构屈服单元数量增加不明显，而当埋深大于100 m时，衬砌结构破坏单元数量剧增，并引起其内力的降低。图6为不同应力释放率下屈服单元数量，结果表明当埋深小于100 m时，应力释放30%和60%2种情况下衬砌结构屈服单元数量基本相同，而当埋深超过100 m时，应力释放60%工况下喷射混凝土衬砌破坏情况明显比应力释放30%严重。造成这一现象的主要原因是应力释放量较大时，引起了节理面的错动破坏，从而使得硐室上覆岩体产生垮落，围岩不仅丧失了自承载能力，且其自身重力作为一种附加荷载作用于衬砌结构，加剧了衬砌的破坏。因此，围岩应力释放量应当以不引起硐室围岩大范围垮落为宜。

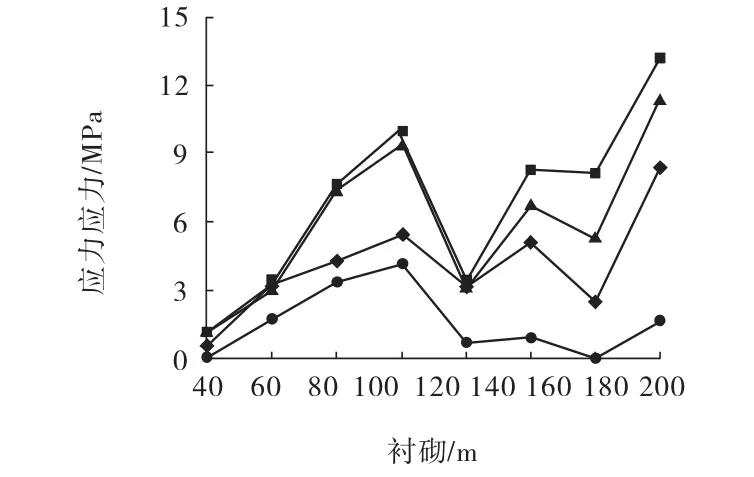
图5 不同埋深下特殊部位衬砌的应力

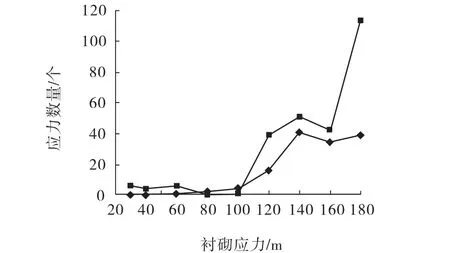
图6 不同埋深下衬砌轴单元轴向屈服数量

3 结论

(1)对于破碎岩体，较大的应力释放率更容易造成硐室的失稳，硐室开挖后应及时施加衬砌，且随着应力释放率的增大支护结构的受力逐渐从拱顶向两帮传递。

(2)随着节理间距的增大，岩体的力学性能趋于增大，有利于围岩的自承载，但存在敏感节理间距影响范围，当节理间距过大或者过小时，对单层衬砌结构的受力影响不大。

(3)节理倾向对围岩的受力特性具有明显的影响，90°倾向节理组更容易引起拱顶冒落和片帮底鼓。

(4)对于Ⅳ、Ⅴ类松散岩体，硐室埋深超过120 m小于60 m(H≥120 m或H≤60 m)时，围岩应力释放较小，支护效果较好；埋深在120 m和60 m(60 m＜H＜120 m)之间时，应力释放60%后施加支护的效果较好。总体而言，当硐室埋深小于120 m时，支护效果比较好。

［1］ 张俊儒，仇文革.隧道单层衬砌研究现状及评述［J］.地下空间与工程学报，2006，2(4):693-699.

［2］ 关宝树.隧道工程设计要点集［M］.北京:人民交通出版社，2003.

［3］ 胡威冬.离散单元法在岩石隧道开挖中的应用研究［D］.成都:西南交通大学，2008.

［4］ 雷远见.顺层边坡稳定性分析［D］.北京:中国科学院，2006.

［5］ 朱维申，李术才，陈卫忠.节理岩体破坏机理和锚固效应及工程应用［M］.北京:科学出版社，2002.

［6］ Brady B H G，Coulthard M A，Lemos J V.A hybrid distinet e-1ement-boundary element method for semi-infinite and infinite body problems［C］∥ Proc.Computer Techniques and Applications Conferenee.［S.l.］:North-Holland Publishers，1984:307-316.

［7］ 刘 君，孔宪京.节理岩体中隧道开挖与支护的数值模拟［J］. 岩土力学，2007，28(2):321-326.

［8］ 冷先伦.层状岩质边坡破坏机理离散元分析［D］.西安:西安交通大学，2005.

［9］ 贺续文，刘 忠，廖 彪，等.基于离散元法的节理岩体边坡稳定性分析［J］. 岩土力学，2011，32(7):2199-2204.

［10］ 郑颖人，王永甫，王 成，等.节理岩体隧道的稳定分析与破坏规律探讨［J］.地下空间与工程学报，2011，7(4):649-656.

［11］ 张承荣，许振华.节理岩体巷道支护作用机理的离散元模拟研究［J］. 现代矿业，2010(4):65-68.

［12］ 赵景彭.节理倾角对层状岩体大断面隧道稳定性研究［J］.铁道建筑，2011(9):58-61.

［13］ 张志强.非贯通裂隙岩体破坏细观特征及其宏观力学参数确定方法［D］.西安:西安理工大学，2009.

［14］ 周顺华，高渠清，崔之鉴.开挖应力释放率计算模型［J］.上海力学，1997，18(1):91-98.

Numerical Simulation Study of Surrounding Rock Excavated in Joint Rock Mass based on Discrete Element Method

Wang Hongying1Zhang Lei2Guo Bin3
(1.College of Mining and Transportation Engineering，Jiangsu Jianzhu Institute；2.State Grid of China Technology College；3.Highway Maintenance Center，Highway Bureau of Binzhou)

The occurrence and mechanics of joint generally determines the integrity of rock mass，and also influences the stability of surrounding rock significantly.This paper mainly analyzes the stress of surrounding rock and lining considering four factors of release ratio of initial stress，distance of joint，integrity of joint and buried depth of tunnel in construction of tunnel with UDEC code.The results show that:①the stress of lining decrease with the increasing release ratio of stress，however，once it reaches certain value，the upper covering rock mass slides and collapses，then the main bearing position turns from invert to vault； ②the increasing distance of joint enhances the integrity of rock mass，which improves the selfbearing capacity and whole stability of surrounding rock；③the inclination angle of joint influences the main bearing position of lining structure；④the yield elements，together with the internal force of lining structure，significantly increase with the increase of buried depth.

Tunnel，Joint rock，Discrete element method，Numerical simulation，Stability

* 国家自然科学基金项目(编号:51204168)。

王红英(1983—)，女，硕士，讲师，221116江苏省徐州市泉山区学苑路26号。

2013-06-11)